AIAA Space 2001 Conference
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Utilization of Halo Orbit§ in Advanced Lunar Operation§
NASA TECHNICAL NOTE NASA TN 0-6365 VI *o M *o d a THE UTILIZATION OF HALO ORBIT§ IN ADVANCED LUNAR OPERATION§ by Robert W. Fmqcbar Godddrd Spctce Flight Center P Greenbelt, Md. 20771 NATIONAL AERONAUTICS AND SPACE ADMINISTRATION WASHINGTON, D. C. JULY 1971 1. Report No. 2. Government Accession No. 3. Recipient's Catalog No. NASA TN D-6365 5. Report Date Jul;v 1971. 6. Performing Organization Code 8. Performing Organization Report No, G-1025 10. Work Unit No. Goddard Space Flight Center 11. Contract or Grant No. Greenbelt, Maryland 20 771 13. Type of Report and Period Covered 2. Sponsoring Agency Name and Address Technical Note J National Aeronautics and Space Administration Washington, D. C. 20546 14. Sponsoring Agency Code 5. Supplementary Notes 6. Abstract Flight mechanics and control problems associated with the stationing of space- craft in halo orbits about the translunar libration point are discussed in some detail. Practical procedures for the implementation of the control techniques are described, and it is shown that these procedures can be carried out with very small AV costs. The possibility of using a relay satellite in.a halo orbit to obtain a continuous com- munications link between the earth and the far side of the moon is also discussed. Several advantages of this type of lunar far-side data link over more conventional relay-satellite systems are cited. It is shown that, with a halo relay satellite, it would be possible to continuously control an unmanned lunar roving vehicle on the moon's far side. Backside tracking of lunar orbiters could also be realized. -

Astrodynamics
Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities -

Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo
Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo To cite this version: Emmanuel Blazquez, Laurent Beauregard, Stéphanie Lizy-Destrez, Finn Ankersen, Francesco Capolupo. Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit. International Symposium on Space Flight Dynamics (ISSFD), Feb 2019, Melbourne, Australia. pp.1408-1413. hal-03200239 HAL Id: hal-03200239 https://hal.archives-ouvertes.fr/hal-03200239 Submitted on 16 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Open Archive Toulouse Archive Ouverte (OATAO) OATAO is an open access repository that collects the wor of some Toulouse researchers and ma es it freely available over the web where possible. This is an author's version published in: h ttps://oatao.univ-toulouse.fr/22865 To cite this version : Blazquez, Emmanuel and Beauregard, Laurent and Lizy-Destrez, Stéphanie and Ankersen, Finn and Capolupo, Francesco Rendezvous Design in a Cislunar Near Rectilinear Halo Orbit. -

Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature -
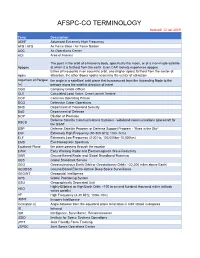
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance -

Asteroid Retrieval Mission
Where you can put your asteroid Nathan Strange, Damon Landau, and ARRM team NASA/JPL-CalTech © 2014 California Institute of Technology. Government sponsorship acknowledged. Distant Retrograde Orbits Works for Earth, Moon, Mars, Phobos, Deimos etc… very stable orbits Other Lunar Storage Orbit Options • Lagrange Points – Earth-Moon L1/L2 • Unstable; this instability enables many interesting low-energy transfers but vehicles require active station keeping to stay in vicinity of L1/L2 – Earth-Moon L4/L5 • Some orbits in this region is may be stable, but are difficult for MPCV to reach • Lunar Weakly Captured Orbits – These are the transition from high lunar orbits to Lagrange point orbits – They are a new and less well understood class of orbits that could be long term stable and could be easier for the MPCV to reach than DROs – More study is needed to determine if these are good options • Intermittent Capture – Weakly captured Earth orbit, escapes and is then recaptured a year later • Earth Orbit with Lunar Gravity Assists – Many options with Earth-Moon gravity assist tours Backflip Orbits • A backflip orbit is two flybys half a rev apart • Could be done with the Moon, Earth or Mars. Backflip orbit • Lunar backflips are nice plane because they could be used to “catch and release” asteroids • Earth backflips are nice orbits in which to construct things out of asteroids before sending them on to places like Earth- Earth or Moon orbit plane Mars cyclers 4 Example Mars Cyclers Two-Synodic-Period Cycler Three-Synodic-Period Cycler Possibly Ballistic Chen, et al., “Powered Earth-Mars Cycler with Three Synodic-Period Repeat Time,” Journal of Spacecraft and Rockets, Sept.-Oct. -

Aas 11-509 Artemis Lunar Orbit Insertion and Science Orbit Design Through 2013
AAS 11-509 ARTEMIS LUNAR ORBIT INSERTION AND SCIENCE ORBIT DESIGN THROUGH 2013 Stephen B. Broschart,∗ Theodore H. Sweetser,y Vassilis Angelopoulos,z David C. Folta,x and Mark A. Woodard{ As of late-July 2011, the ARTEMIS mission is transferring two spacecraft from Lissajous orbits around Earth-Moon Lagrange Point #1 into highly-eccentric lunar science orbits. This paper presents the trajectory design for the transfer from Lissajous orbit to lunar orbit in- sertion, the period reduction maneuvers, and the science orbits through 2013. The design accommodates large perturbations from Earth’s gravity and restrictive spacecraft capabili- ties to enable opportunities for a range of heliophysics and planetary science measurements. The process used to design the highly-eccentric ARTEMIS science orbits is outlined. The approach may inform the design of future eccentric orbiter missions at planetary moons. INTRODUCTION The Acceleration, Reconnection, Turbulence and Electrodynamics of the Moons Interaction with the Sun (ARTEMIS) mission is currently operating two spacecraft in lunar orbit under funding from the Heliophysics and Planetary Science Divisions with NASA’s Science Missions Directorate. ARTEMIS is an extension to the successful Time History of Events and Macroscale Interactions during Substorms (THEMIS) mission [1] that has relocated two of the THEMIS spacecraft from Earth orbit to the Moon [2, 3, 4]. ARTEMIS plans to conduct a variety of scientific studies at the Moon using the on-board particle and fields instrument package [5, 6]. The final portion of the ARTEMIS transfers involves moving the two ARTEMIS spacecraft, known as P1 and P2, from Lissajous orbits around the Earth-Moon Lagrange Point #1 (EML1) to long-lived, eccentric lunar science orbits with periods of roughly 28 hr. -

Dynamical Analysis of Rendezvous and Docking with Very Large Space Infrastructures in Non-Keplerian Orbits
DYNAMICAL ANALYSIS OF RENDEZVOUS AND DOCKING WITH VERY LARGE SPACE INFRASTRUCTURES IN NON-KEPLERIAN ORBITS Andrea Colagrossi ∗, Michele` Lavagna y, Simone Flavio Rafano Carna` z Politecnico di Milano Department of Aerospace Science and Technology Via La Masa 34 – 20156 Milan (MI) – Italy ABSTRACT the whole mission scenario is the so called Evolvable Deep Space Habitat: a modular space station in lunar vicinity. A space station in the vicinity of the Moon can be exploited At the current level of study, the optimum location for as a gateway for future human and robotic exploration of the space infrastructure of this kind has not yet been determined, Solar System. The natural location for a space system of this but a favorable solution can be about one of the Earth-Moon kind is about one of the Earth-Moon libration points. libration points, such as in a EML2 (Earth-Moon Lagrangian The study addresses the dynamics during rendezvous and Point no 2) Halo orbit. Moreover, the final configuration of docking operations with a very large space infrastructure in a the entire system is still to be defined, but it is already clear EML2 Halo orbit. The model takes into account the coupling that in order to assemble the structure several rendezvous and effects between the orbital and the attitude motion in a Circular docking activities will be carried out, many of which to be Restricted Three-Body Problem environment. The flexibility completely automated. of the system is included, and the interaction between the Unfortunately, the current knowledge about rendezvous in modes of the structure and those related with the orbital motion cis-lunar orbits is minimal and it is usually limited to point- is investigated. -

An Examination of the Mass Limit for Stability at the Triangular Lagrange
San Jose State University SJSU ScholarWorks Master's Theses Master's Theses and Graduate Research Spring 2015 An Examination of the Mass Limit for Stability at the Triangular Lagrange Points for a Three-Body System and a Special Case of the Four-Body Problem Sean Kemp San Jose State University Follow this and additional works at: https://scholarworks.sjsu.edu/etd_theses Recommended Citation Kemp, Sean, "An Examination of the Mass Limit for Stability at the Triangular Lagrange Points for a Three-Body System and a Special Case of the Four-Body Problem" (2015). Master's Theses. 4546. DOI: https://doi.org/10.31979/etd.4tf8-hnqx https://scholarworks.sjsu.edu/etd_theses/4546 This Thesis is brought to you for free and open access by the Master's Theses and Graduate Research at SJSU ScholarWorks. It has been accepted for inclusion in Master's Theses by an authorized administrator of SJSU ScholarWorks. For more information, please contact [email protected]. AN EXAMINATION OF THE MASS LIMIT FOR STABILITY AT THE TRIANGULAR LAGRANGE POINTS FOR A THREE-BODY SYSTEM AND A SPECIAL CASE OF THE FOUR-BODY PROBLEM A Thesis Presented to The Faculty of the Department of Physics and Astronomy San José State University In Partial Fulllment of the Requirements for the Degree Master of Science by Sean P. Kemp May 2015 c 2015 Sean P. Kemp ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled AN EXAMINATION OF THE MASS LIMIT FOR STABILITY AT THE TRIANGULAR LAGRANGE POINTS FOR A THREE-BODY SYSTEM AND A SPECIAL CASE OF THE FOUR-BODY PROBLEM by Sean P. -

Design of Small Circular Halo Orbit Around L2
Design of Small Circular Halo Orbit around L2 Kohta Tarao* and Jun’ichiro Kawaguchi** *Graduate Student, Department of Aeronautics and Astronautics, School of Engineering, The University of Tokyo ** The Institute of Space and Astronautics Science / Japan Aerospace Exploration Agency (ISAS/JAXA) 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, JAPAN. Abstract A Lagrange point of Sun-Earth system, L1 or L2 is conceived one of the best point for astronomy and connection ports for outer planets. This paper describes a new useful control method for realizing and keeping small circular Halo orbits around the L2 point. First, a control law is mathematically derived from the restricted three body problem formulation and the associated properties are discussed. And next, some useful cases for the space mission are verified numerically using real ephemeris. The resulted Halo orbit is compact and circular realized with satisfactorily small thrust. The paper concludes the strategy is applied to many kinds of missions. L2 点周りの小円ハロー軌道設計 多羅尾康太(東大・工・院)、川口淳一郎(ISAS/JAXA) 摘要 太陽―月・地球系におけるラグランジュ点の中で、L2 点は太陽と地球との距離がほぼ一定で、太 陽、地球との幾何学的関係が保たれ、またダウンリンク通信が太陽の影響を受けない点で L1 点よ りも有利である。そのため L2 点周辺の軌道は、赤外線天文衛星や外惑星探査のための起・終点と しての宇宙港の軌道として利用が考えられている。本論文では、新しい制御法により L2 点回りに 小さな円形の Halo 軌道が作れることを示す。まず初めに、円制限三体問題における線形化された 方程式から理論的に制御則を導く。その後、実軌道要素を用いて軌道制御方法を検証する。軌道制 御に必要な推力は十分小さく大変実用的な制御方法である。 INTRODUCTION million kilometers and also due to its highly alternating geometry. A Lissajous orbit also exists A Lagrange point is the point where the gravity of around the L2 point naturally, however, the orbital two planets such as Sun and Earth is equal to plane rotates and the solar power availability is centrifugal force by their circular motions. L1 and often restricted due to the shadow by the Earth. -

What Is the Interplanetary Superhighway?
What is the InterPlanetary Suppgyerhighway? Kathleen Howell Purdue University Lo and Ross Trajectory Key Space Technology Mission-Enabling Technology Not All Technology is hardware! The InterPlanetary Superhighway (IPS) • LELow Energy ObitfSOrbits for Space Mi Miissions • InterPlanetary Superhighway—“a vast network of winding tunnels in space” that connects the Sun , the planets, their moons, AND many other destinations • Systematic mapping properly known as InterPlanetary Transport Network Simó, Gómez, Masdemont / Lo, Howell, Barden / Howell, Folta / Lo, Ross / Koon, Lo, Marsden, Ross / Marchand, Howell, Lo / Scheeres, Villac/ ……. Originates with Poincaré (1892) Applications to wide range of fields Different View of Problems in N-Bodies • Much more than Kepler and Newton imagined • Computationally challenging Poincaré (1854-1912) “Mathematics is the art of giving the same name to different things” Jules Henri Poincaré NBP Play 3BP Wang 2BP New Era in Celestial Mechanics Pioneering Work: Numerical Exploration by Hand (Breakwell, Farquhar and Dunham) Current Libration Point Missions Goddard Space Flight Center • z WIND SOHO ACE MAPGENESIS NGST Courtesy of D. Folta, GSFC Multi-Body Problem Orbit propagated for 4 conic periods: • Change our perspective 4*19 days = 75.7 days Earth Earth Sun To Sun Inertial View RotatingRotating View View Inertial View (Ro ta tes w ith two b odi es) Aeronautics and Astronautics Multi-Body Problem • Change our perspective • Effects of added gravity fields Earth Earth TSTo Sun Rotating View Inertial View Equilibrium -

Stability of the Lagrange Points, L4 and L5
Stability of the Lagrange Points, L4 and L5 Thomas Greenspan January 7, 2014 Abstract A proof of the stability of the non collinear Lagrange Points, L4 and L5. We will start by covering the basics of stability, stating a theorem (without proof) with a few corollaries, and then turn to the Lagrange points, proving first the stability of all Lagrange points in the z-direction and then restricting our attention to the the points, L4 and L5. Introduction The three body problem is one that has been studied for many centuries. It consists of considering 3 bodies, subject to only to mutually attracting forces (determined by the inverse square force, gravitation) and to solve for the motions of the three bodies. This task can be extremely complicated and, following Poincar´e's example, most mathematicians and physicists have interested themselves in the finding periodic solutions to the problem, that is, where x(t) = x(t + T ) where T is the period [3]. Indeed not only does this offer a useful framework from within which to work, but also describes states that are most applicable and useful to real world situations. Finding these periodic solutions is by no means trivial. It is a problem that has been worked on for centuries and still is in modern times, one of the latest publications dealing with it as recent as March of 2013 [9]. Among the first to interest themselves in and find solutions to the 3 body problem were Leonhard Euler in 1765 and Joseph Lagrange in 1772 [3]. In his publication, Essai sur le probl`emedes trois corps (Essay on the 3-Body Problem), Lagrange proposed a method that had never been used until then, that of considering only the distances between the three bodies rather than their absolute positions [2].