DOCSLIB.ORG

Lecture 2 Geometry Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 2 Geometry Of Lecture 2 Geometry of LPs∗ Last time we saw that, given a (minimizing) linear program in equational form, one of the following three possibilities is true: 1. The LP is infeasible. 2. The optimal value of the LP is −∞ (i.e., the LP does not have a bounded optimum). 3. A basic feasible solution exists that achieves the optimal value. 2.1 Finding a basic feasible solution Suppose we have an LP in equational form: minf cT x j Ax = b; x ≥ 0 g; where A is an m × n matrix of rank m: Recall how we might attempt to find a BFS to this LP: Let B ⊆ [n], with jBj = m, such that AB (the set of columns of A corresponding to the elements of B) is linearly independent. (Such a set of columns exists because A has full rank.) Let N = [n] n B be the indices of the n columns of A that are not in B. Since AB is invertible, we can define a vector x 2 R by −1 xB = AB b; xN = 0: By construction, x is a basic solution. If x is also feasible (i.e., if x ≥ 0), then it is a BFS. Fact 2.1. Every LP in equational form that is feasible has a BFS. (Note that this BFS may or may not be optimal.) Proof. Pick some feasible pointx ~ 2 Rn. (In particular, sincex ~ is feasible,x ~ ≥ 0.) Let P = f j j x~j > 0 g *Lecturer: Anupam Gupta. Scribe: Brian Kell. 1 LECTURE 2. GEOMETRY OF LPS 2 be the set of coordinates ofx ~ that are nonzero. We consider two cases, depending on whether the columns of AP are linearly independent. Case 1. The columns of AP are linearly independent. Then we may extend P to a basis B, i.e., a subset P ⊆ B ⊆ [n] with jBj = m such that the columns of AB are also linearly independent. Let N = [n] n B; thenx ~N = 0 (because P ⊆ B). In addition, since −1 Ax~ = b, we have ABx~B = b, sox ~ = AB b. Sox ~ is a basic solution; since it is feasible by −1 assumption, it is a BFS. (Note, by the way, that the equationx ~ = AB b means thatx ~ is the unique solution to Ax = b having xN = 0.) Case 2. The columns of AP are linearly dependent. Let N = [n] n P . Then, by the n definition of linear dependence, there exists a nonzero vector w 2 R with wN = 0 such that AP wP = 0. For any λ 2 R, the vectorx ~ + λw satisfies A(~x + λw) = b, because A(~x + λw) = Ax~ + λAw = b + 0 = b: Becausex ~N = 0 and wN = 0, we have (~x + λw)N = 0, sox ~ + λw has no more nonzero entries thanx ~ does. Sincex ~P > 0, for sufficiently small > 0 bothx ~ + w andx ~ − w are feasible (i.e,x ~ ± w ≥ 0). Let η = supf > 0 j x~ ± w ≥ 0 g be the largest such ; then one of x~ ± ηw has one more zero coordinate thanx ~ does. We can repeat this until we find a feasible solution with no more than m nonzero coordinates, at which point Case 1 applies and we have found a BFS. (Intuitively, for sufficiently small > 0, one ofx ~ ± w is moving toward a nonnegativity constraint, that is, toward the boundary of the nonnegative orthant. When becomes just large enough that the pointx ~ ± w reaches the boundary of the nonnegative orthant, we have made one more coordinate of the point zero.) 2.2 Geometric definitions Definition 2.2. Given points x; y 2 Rn, a point z 2 Rn is a convex combination of x and y if z = λx + (1 − λ)y for some λ 2 [0; 1]. Definition 2.3. A set X ⊆ Rn is convex if the convex combination of any two points in X is also in X; that is, for all x; y 2 X and all λ 2 [0; 1], the point λx + (1 − λ)y is in X. Definition 2.4. A function f : Rn ! R is convex if for all points x; y 2 Rn and all λ 2 [0; 1] we have fλx + (1 − λ)y ≤ λf(x) + (1 − λ)f(y): Fact 2.5. If P ⊆ Rn is a convex set and f : Rn ! R is a convex function, then, for any t 2 R, the set Q = f x 2 P j f(x) ≤ t g is also convex. LECTURE 2. GEOMETRY OF LPS 3 Proof. For all x1; x2 2 Q and all λ 2 [0; 1], we have f λx1 + (1 − λ)x2 ≤ λf(x1) + (1 − λ)f(x2) ≤ λt + (1 − λ)t = t; so λx1 + (1 − λ)x2 2 Q. Fact 2.6. The intersection of two convex sets is convex. n Proof. Let P; Q ⊆ R be convex sets, and let x1; x2 2 P \ Q. Let λ 2 [0; 1]. Because x1; x2 2 P and P is convex, we have λx1 + (1 − λ)x2 2 P ; likewise, λx1 + (1 − λ)x2 2 Q. So λx1 + (1 − λ)x2 2 P \ Q. Definition 2.7. A set S ⊆ Rn is a subspace if it is closed under addition and scalar multi- plication. Equivalently, S is a subspace if S = f x 2 Rn j Ax = 0 g for some matrix A. Definition 2.8. The dimension of a subspace S ⊆ Rn, written dim(S), is the size of the largest linearly independent set of vectors contained in S. Equivalently, dim(S) = n − rank(A). 0 n 0 Definition 2.9. A set S ⊆ R is an affine subspace if S = f x0 + y j y 2 S g for some n n 0 0 subspace S ⊆ R and some vector x0 2 R . In this case the dimension of S , written dim(S ), is defined to equal the dimension of S. Equivalently, S0 is an affine subspace if S0 = f x 2 Rn j Ax = b g for some matrix A and some vector b. Definition 2.10. The dimension of a set X ⊆ Rn, written dim(X), is the dimension of the minimal affine subspace that contains X. 0 0 Note that if S1 and S2 are two affine subspaces both containing X, then their intersec- 0 0 tion S1 \ S2 is an affine subspace containing X. Hence there is a unique minimal affine subspace that contains X, so dim(X) is well defined. Equivalently, given x0 2 X, the dimension of X is the largest number k for which there exist points x1; x2; : : : ; xk 2 X such that the set fx1 − x0; x2 − x0; : : : ; xk − x0g is linearly independent. Note that the definition of the dimension of a set X agrees with the definition of the dimension of an affine subspace if X happens to be an affine subspace, and the definition of the dimension of an affine subspace S0 agrees with the definition of the dimension of a subspace if S0 happens to be a subspace. Definition 2.11. A set H ⊆ Rn is a hyperplane if H = f x 2 Rn j aT x = b g for some nonzero a 2 Rn and some b 2 R. A hyperplane is an affine subspace of dimension n − 1. Definition 2.12. A set H0 ⊆ Rn is a (closed) halfspace if H0 = f x 2 Rn j aT ≥ b g for some nonzero a 2 Rn and some b 2 R. LECTURE 2. GEOMETRY OF LPS 4 A hyperplane can be written as the intersection of two halfspaces: n T n T n T f x 2 R j a x = b g = f x 2 R j a x ≥ b g \ f x 2 R j −a x ≥ −b g: Both hyperplanes and halfspaces are convex sets. Therefore the feasible region of an LP is convex, because it is the intersection of halfspaces and hyperplanes. The dimension of the feasible region of an LP in equational form, having n variables and m linearly independent constraints (equalities), is no greater than n − m, because it is contained in the intersection of m distinct hyperplanes, each of which is an affine subspace of dimension n − 1. (The dimension of the feasible region may be less than n − m, because of the nonnegativity constraints, for instance.) For example, the region in R3 defined by x1 + x2 + x3 = 1; x ≥ 0 is a 2-dimensional triangle; here, n − m = 3 − 1 = 2. (Note, however, that if the constraint were x1 + x2 + x3 = 0, the region would have dimension 0.) 3 Figure 2.1: The region f x 2 R j x1 + x2 + x3 = 1; x ≥ 0 g. Definition 2.13. A polyhedron in Rn is the intersection of finitely many halfspaces. For example, feasible regions of LPs are polyhedra. Definition 2.14. A polytope is a bounded polyhedron, that is, a polyhedron P for which + there exists B 2 R such that kxk2 ≤ B for all x 2 P . LECTURE 2. GEOMETRY OF LPS 5 Both polyhedra and polytopes are convex. Definition 2.15. Given a polyhedron P ⊆ Rn, a point x 2 P is a vertex of P if there exists c 2 Rn such that cT x < cT y for all y 2 P , y 6= x. Supposex ^ is a vertex of a polyhedron P ⊆ Rn. Let c be as in the definition above. Take K = cT x^. Then for all y 2 P we have cT y ≥ K, so the polyhedron P is contained in the halfspace f x 2 Rn j cT x ≥ K g, i.e., P lies entirely on one side of the hyperplane f x 2 Rn j cT x = K g.
Load more

Recommended publications
  • Lecture 3 1 Geometry of Linear Programs
    ORIE 6300 Mathematical Programming I September 2, 2014 Lecture 3 Lecturer: David P. Williamson Scribe: Divya Singhvi Last time we discussed how to take dual of an LP in two different ways. Today we will talk about the geometry of linear programs. 1 Geometry of Linear Programs First we need some definitions. Definition 1 A set S ⊆ <n is convex if 8x; y 2 S, λx + (1 − λ)y 2 S, 8λ 2 [0; 1]. Figure 1: Examples of convex and non convex sets Given a set of inequalities we define the feasible region as P = fx 2 <n : Ax ≤ bg. We say that P is a polyhedron. Which points on this figure can have the optimal value? Our intuition from last time is that Figure 2: Example of a polyhedron. \Circled" corners are feasible and \squared" are non feasible optimal solutions to linear programming problems occur at \corners" of the feasible region. What we'd like to do now is to consider formal definitions of the \corners" of the feasible region. 3-1 One idea is that a point in the polyhedron is a corner if there is some objective function that is minimized there uniquely. Definition 2 x 2 P is a vertex of P if 9c 2 <n with cT x < cT y; 8y 6= x; y 2 P . Another idea is that a point x 2 P is a corner if there are no small perturbations of x that are in P . Definition 3 Let P be a convex set in <n. Then x 2 P is an extreme point of P if x cannot be written as λy + (1 − λ)z for y; z 2 P , y; z 6= x, 0 ≤ λ ≤ 1.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
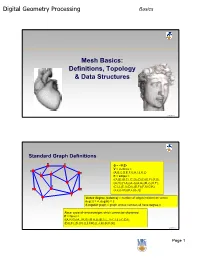
  • Digital Geometry Processing Mesh Basics
    Digital Geometry Processing Basics Mesh Basics: Definitions, Topology & Data Structures 1 © Alla Sheffer Standard Graph Definitions G = <V,E> V = vertices = {A,B,C,D,E,F,G,H,I,J,K,L} E = edges = {(A,B),(B,C),(C,D),(D,E),(E,F),(F,G), (G,H),(H,A),(A,J),(A,G),(B,J),(K,F), (C,L),(C,I),(D,I),(D,F),(F,I),(G,K), (J,L),(J,K),(K,L),(L,I)} Vertex degree (valence) = number of edges incident on vertex deg(J) = 4, deg(H) = 2 k-regular graph = graph whose vertices all have degree k Face: cycle of vertices/edges which cannot be shortened F = faces = {(A,H,G),(A,J,K,G),(B,A,J),(B,C,L,J),(C,I,L),(C,D,I), (D,E,F),(D,I,F),(L,I,F,K),(L,J,K),(K,F,G)} © Alla Sheffer Page 1 Digital Geometry Processing Basics Connectivity Graph is connected if there is a path of edges connecting every two vertices Graph is k-connected if between every two vertices there are k edge-disjoint paths Graph G’=<V’,E’> is a subgraph of graph G=<V,E> if V’ is a subset of V and E’ is the subset of E incident on V’ Connected component of a graph: maximal connected subgraph Subset V’ of V is an independent set in G if the subgraph it induces does not contain any edges of E © Alla Sheffer Graph Embedding Graph is embedded in Rd if each vertex is assigned a position in Rd Embedding in R2 Embedding in R3 © Alla Sheffer Page 2 Digital Geometry Processing Basics Planar Graphs Planar Graph Plane Graph Planar graph: graph whose vertices and edges can Straight Line Plane Graph be embedded in R2 such that its edges do not intersect Every planar graph can be drawn as a straight-line plane graph ©
    [Show full text]
  • Extreme Points and Basic Solutions
    EXTREME POINTS AND BASIC SOLUTIONS: In Linear Programming, the feasible region in Rn is defined by P := {x ∈ Rn | Ax = b, x ≥ 0}. The set P , as we have seen, is a convex subset of Rn. It is called a convex polytope. The term convex polyhedron refers to convex polytope which is bounded. Polytopes in two dimensions are often called polygons. Recall that the vertices of a convex polytope are what we called extreme points of that set. Recall that extreme points of a convex set are those which cannot be represented as a proper convex combination of two other (distinct) points of the convex set. It may, or may not be the case that a convex set has any extreme points as shown by the example in R2 of the strip S := {(x, y) ∈ R2 | 0 ≤ x ≤ 1, y ∈ R}. On the other hand, the square defined by the inequalities |x| ≤ 1, |y| ≤ 1 has exactly four extreme points, while the unit disk described by the ineqality x2 + y2 ≤ 1 has infinitely many. These examples raise the question of finding conditions under which a convex set has extreme points. The answer in general vector spaces is answered by one of the “big theorems” called the Krein-Milman Theorem. However, as we will see presently, our study of the linear programming problem actually answers this question for convex polytopes without needing to call on that major result. The algebraic characterization of the vertices of the feasible polytope confirms the obser- vation that we made by following the steps of the Simplex Algorithm in our introductory example.
    [Show full text]
  • The Feasible Region for Consecutive Patterns of Permutations Is a Cycle Polytope
    Séminaire Lotharingien de Combinatoire XX (2020) Proceedings of the 32nd Conference on Formal Power Article #YY, 12 pp. Series and Algebraic Combinatorics (Ramat Gan) The feasible region for consecutive patterns of permutations is a cycle polytope Jacopo Borga∗1, and Raul Penaguiaoy 1 1Department of Mathematics, University of Zurich, Switzerland Abstract. We study proportions of consecutive occurrences of permutations of a given size. Specifically, the feasible limits of such proportions on large permutations form a region, called feasible region. We show that this feasible region is a polytope, more precisely the cycle polytope of a specific graph called overlap graph. This allows us to compute the dimension, vertices and faces of the polytope. Finally, we prove that the limits of classical occurrences and consecutive occurrences are independent, in some sense made precise in the extended abstract. As a consequence, the scaling limit of a sequence of permutations induces no constraints on the local limit and vice versa. Keywords: permutation patterns, cycle polytopes, overlap graphs. This is a shorter version of the preprint [11] that is currently submitted to a journal. Many proofs and details omitted here can be found in [11]. 1 Introduction 1.1 Motivations Despite not presenting any probabilistic result here, we give some motivations that come from the study of random permutations. This is a classical topic at the interface of combinatorics and discrete probability theory. There are two main approaches to it: the first concerns the study of statistics on permutations, and the second, more recent, looks arXiv:2003.12661v2 [math.CO] 30 Jun 2020 for the limits of permutations themselves.
    [Show full text]
  • Linear Programming
    Stanford University | CS261: Optimization Handout 5 Luca Trevisan January 18, 2011 Lecture 5 In which we introduce linear programming. 1 Linear Programming A linear program is an optimization problem in which we have a collection of variables, which can take real values, and we want to find an assignment of values to the variables that satisfies a given collection of linear inequalities and that maximizes or minimizes a given linear function. (The term programming in linear programming, is not used as in computer program- ming, but as in, e.g., tv programming, to mean planning.) For example, the following is a linear program. maximize x1 + x2 subject to x + 2x ≤ 1 1 2 (1) 2x1 + x2 ≤ 1 x1 ≥ 0 x2 ≥ 0 The linear function that we want to optimize (x1 + x2 in the above example) is called the objective function.A feasible solution is an assignment of values to the variables that satisfies the inequalities. The value that the objective function gives 1 to an assignment is called the cost of the assignment. For example, x1 := 3 and 1 2 x2 := 3 is a feasible solution, of cost 3 . Note that if x1; x2 are values that satisfy the inequalities, then, by summing the first two inequalities, we see that 3x1 + 3x2 ≤ 2 that is, 1 2 x + x ≤ 1 2 3 2 1 1 and so no feasible solution has cost higher than 3 , so the solution x1 := 3 , x2 := 3 is optimal. As we will see in the next lecture, this trick of summing inequalities to verify the optimality of a solution is part of the very general theory of duality of linear programming.
    [Show full text]
  • Math 112 Review for Exam Ii (Ws 12 -18)
    MATH 112 REVIEW FOR EXAM II (WS 12 -18) I. Derivative Rules • There will be a page or so of derivatives on the exam. You should know how to apply all the derivative rules. (WS 12 and 13) II. Functions of One Variable • Be able to find local optima, and to distinguish between local and global optima. • Be able to find the global maximum and minimum of a function y = f(x) on the interval from x = a to x = b, using the fact that optima may only occur where f(x) has a horizontal tangent line and at the endpoints of the interval. Step 1: Compute the derivative f’(x). Step 2: Find all critical points (values of x at which f’(x) = 0.) Step 3: Plug all the values of x from Step 2 that are in the interval from a to b and the endpoints of the interval into the function f(x). Step 4: Sketch a rough graph of f(x) and pick off the global max and min. • Understand the following application: Maximizing TR(q) starting with a demand curve. (WS 15) • Understand how to use the Second Derivative Test. (WS 16) If a is a critical point for f(x) (that is, f’(a) = 0), and the second derivative is: f ’’(a) > 0, then f(x) has a local min at x = a. f ’’(a) < 0, then f(x) has a local max at x = a. f ’’(a) = 0, then the test tells you nothing. IMPORTANT! For the Second Derivative Test to work, you must have f’(a) = 0 to start with! For example, if f ’’(a) > 0 but f ’(a) ≠ 0, then the graph of f(x) is concave up at x = a but f(x) does not have a local min there.
    [Show full text]
  • 15 BASIC PROPERTIES of CONVEX POLYTOPES Martin Henk, J¨Urgenrichter-Gebert, and G¨Unterm
    15 BASIC PROPERTIES OF CONVEX POLYTOPES Martin Henk, J¨urgenRichter-Gebert, and G¨unterM. Ziegler INTRODUCTION Convex polytopes are fundamental geometric objects that have been investigated since antiquity. The beauty of their theory is nowadays complemented by their im- portance for many other mathematical subjects, ranging from integration theory, algebraic topology, and algebraic geometry to linear and combinatorial optimiza- tion. In this chapter we try to give a short introduction, provide a sketch of \what polytopes look like" and \how they behave," with many explicit examples, and briefly state some main results (where further details are given in subsequent chap- ters of this Handbook). We concentrate on two main topics: • Combinatorial properties: faces (vertices, edges, . , facets) of polytopes and their relations, with special treatments of the classes of low-dimensional poly- topes and of polytopes \with few vertices;" • Geometric properties: volume and surface area, mixed volumes, and quer- massintegrals, including explicit formulas for the cases of the regular simplices, cubes, and cross-polytopes. We refer to Gr¨unbaum [Gr¨u67]for a comprehensive view of polytope theory, and to Ziegler [Zie95] respectively to Gruber [Gru07] and Schneider [Sch14] for detailed treatments of the combinatorial and of the convex geometric aspects of polytope theory. 15.1 COMBINATORIAL STRUCTURE GLOSSARY d V-polytope: The convex hull of a finite set X = fx1; : : : ; xng of points in R , n n X i X P = conv(X) := λix λ1; : : : ; λn ≥ 0; λi = 1 : i=1 i=1 H-polytope: The solution set of a finite system of linear inequalities, d T P = P (A; b) := x 2 R j ai x ≤ bi for 1 ≤ i ≤ m ; with the extra condition that the set of solutions is bounded, that is, such that m×d there is a constant N such that jjxjj ≤ N holds for all x 2 P .
    [Show full text]
  • Frequently Asked Questions in Polyhedral Computation
    Frequently Asked Questions in Polyhedral Computation http://www.ifor.math.ethz.ch/~fukuda/polyfaq/polyfaq.html Komei Fukuda Swiss Federal Institute of Technology Lausanne and Zurich, Switzerland [email protected] Version June 18, 2004 Contents 1 What is Polyhedral Computation FAQ? 2 2 Convex Polyhedron 3 2.1 What is convex polytope/polyhedron? . 3 2.2 What are the faces of a convex polytope/polyhedron? . 3 2.3 What is the face lattice of a convex polytope . 4 2.4 What is a dual of a convex polytope? . 4 2.5 What is simplex? . 4 2.6 What is cube/hypercube/cross polytope? . 5 2.7 What is simple/simplicial polytope? . 5 2.8 What is 0-1 polytope? . 5 2.9 What is the best upper bound of the numbers of k-dimensional faces of a d- polytope with n vertices? . 5 2.10 What is convex hull? What is the convex hull problem? . 6 2.11 What is the Minkowski-Weyl theorem for convex polyhedra? . 6 2.12 What is the vertex enumeration problem, and what is the facet enumeration problem? . 7 1 2.13 How can one enumerate all faces of a convex polyhedron? . 7 2.14 What computer models are appropriate for the polyhedral computation? . 8 2.15 How do we measure the complexity of a convex hull algorithm? . 8 2.16 How many facets does the average polytope with n vertices in Rd have? . 9 2.17 How many facets can a 0-1 polytope with n vertices in Rd have? . 10 2.18 How hard is it to verify that an H-polyhedron PH and a V-polyhedron PV are equal? .
    [Show full text]
  • Points, Lines, and Planes a Point Is a Position in Space. a Point Has No Length Or Width Or Thickness
    Points, Lines, and Planes A Point is a position in space. A point has no length or width or thickness. A point in geometry is represented by a dot. To name a point, we usually use a (capital) letter. A A (straight) line has length but no width or thickness. A line is understood to extend indefinitely to both sides. It does not have a beginning or end. A B C D A line consists of infinitely many points. The four points A, B, C, D are all on the same line. Postulate: Two points determine a line. We name a line by using any two points on the line, so the above line can be named as any of the following: ! ! ! ! ! AB BC AC AD CD Any three or more points that are on the same line are called colinear points. In the above, points A; B; C; D are all colinear. A Ray is part of a line that has a beginning point, and extends indefinitely to one direction. A B C D A ray is named by using its beginning point with another point it contains. −! −! −−! −−! In the above, ray AB is the same ray as AC or AD. But ray BD is not the same −−! ray as AD. A (line) segment is a finite part of a line between two points, called its end points. A segment has a finite length. A B C D B C In the above, segment AD is not the same as segment BC Segment Addition Postulate: In a line segment, if points A; B; C are colinear and point B is between point A and point C, then AB + BC = AC You may look at the plus sign, +, as adding the length of the segments as numbers.
    [Show full text]
  • The Feasible Region for Consecutive Patterns of Permutations Is a Cycle Polytope
    Algebraic Combinatorics Draft The feasible region for consecutive patterns of permutations is a cycle polytope Jacopo Borga & Raul Penaguiao Abstract. We study proportions of consecutive occurrences of permutations of a given size. Specifically, the limit of such proportions on large permutations forms a region, called feasible region. We show that this feasible region is a polytope, more precisely the cycle polytope of a specific graph called overlap graph. This allows us to compute the dimension, vertices and faces of the polytope, and to determine the equations that define it. Finally we prove that the limit of classical occurrences and consecutive occurrences are in some sense independent. As a consequence, the scaling limit of a sequence of permutations induces no constraints on the local limit and vice versa. (1,0,0,0,0,0) 1 1 (0; 2 ; 2 ; 0; 0; 0) 1 1 1 1 (0; 0; 2 ; 2 ; 0; 0) (0; 2 ; 0; 2 ; 0; 0) 1 1 (0; 0; 0; 2 ; 2 ; 0) arXiv:1910.02233v2 [math.CO] 30 Jun 2020 Figure 1. The four-dimensional polytope P3 given by the six pat- terns of size three (see Eq. (2) for a precise definition). We highlight in light-blue one of the six three-dimensional facets of P3. This facet is a pyramid with square base. The polytope itself is a four-dimensional pyramid, whose base is the highlighted facet. This paper has been prepared using ALCO author class on 1st July 2020. Keywords. Permutation patterns, cycle polytopes, overlap graphs. Acknowledgements. This work was completed with the support of the SNF grants number 200021- 172536 and 200020-172515.
    [Show full text]
  • Mathematical Modelling and Applications of Particle Swarm Optimization
    Master’s Thesis Mathematical Modelling and Simulation Thesis no: 2010:8 Mathematical Modelling and Applications of Particle Swarm Optimization by Satyobroto Talukder Submitted to the School of Engineering at Blekinge Institute of Technology In partial fulfillment of the requirements for the degree of Master of Science February 2011 Contact Information: Author: Satyobroto Talukder E-mail: [email protected] University advisor: Prof. Elisabeth Rakus-Andersson Department of Mathematics and Science, BTH E-mail: [email protected] Phone: +46455385408 Co-supervisor: Efraim Laksman, BTH E-mail: [email protected] Phone: +46455385684 School of Engineering Internet : www.bth.se/com Blekinge Institute of Technology Phone : +46 455 38 50 00 SE – 371 79 Karlskrona Fax : +46 455 38 50 57 Sweden ii ABSTRACT Optimization is a mathematical technique that concerns the finding of maxima or minima of functions in some feasible region. There is no business or industry which is not involved in solving optimization problems. A variety of optimization techniques compete for the best solution. Particle Swarm Optimization (PSO) is a relatively new, modern, and powerful method of optimization that has been empirically shown to perform well on many of these optimization problems. It is widely used to find the global optimum solution in a complex search space. This thesis aims at providing a review and discussion of the most established results on PSO algorithm as well as exposing the most active research topics that can give initiative for future work and help the practitioner improve better result with little effort. This paper introduces a theoretical idea and detailed explanation of the PSO algorithm, the advantages and disadvantages, the effects and judicious selection of the various parameters.
    [Show full text]