DOCSLIB.ORG

Physics Foreword

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

PHYSICS FOREWORD PHYSICS Today, perhaps more than ever, science holds the key to our future. At Our range is continuously being expanded with new products. We invite Frederiksen, we believe that encouraging enthusiasm for science is not you to visit our website to see what's new, and get inspiration and ideas. an additional option – we simply have to inspire innovative young minds At Frederiksen, we like to do more than simply supply goods. Many of if we are to meet the challenges of our future. Why? Because science the products also include extras such as instructions or other support ma­ matters, and because the rising generation of scientists, engineers and terial, prepared by us or members of our network. One important technicians are shaped in a classroom. aspect of our service is our employees, with their scienti­ We know that not everybody is meant to be a scientist. But we believe fic backgrounds, who are always ready to help and that everybody has the right to learn. And learning is encouraged through answer your questions. dedicated teachers and great teaching conditions. II CONTENTS Weights and measures 1 - 8 Fluids, air and heat 9 - 22 Waves, sound, light and optics 23 - 54 Mechanics 55 - 74 Jens Vangklide, CEO Basic electrical equipment 75 - 98 Electrical circuits 99 - 112 Frederiksen Scientific A/S Viaduktvej 35 . DK­6870 Ølgod, Denmark Electric and magnetic fields 113 - 136 Atomic and nuclear physics 137 - 160 Tel. +45 7524 4966 Fax +45 7524 6282 Energy 161 - 174 [email protected] www.frederiksen.eu Geosciences 175 - 188 Opening hours: Astronomy 189 - 194 Monday­Thursday: 8.00­16.00 Laboratory fixtures and fittings 195 - 207 Friday: 8.00­15.30 I NEW Speedgate Olympiad box 1 Page 59 Page 40 iPlug energy meter Page 91 Lens section set Olympiad box 2 Page 50 Page 40 Microphone Page 29 II NEW LCR circuit maker Page 105 Voltameter, student version New, more durable design Page 111 Rotating globe Satellite view 11 cm Page 188 Telescope Cosmos 90GT WiF Page 192 Speed of light Spark detector Page 54 Page 152 III Conditions of sale Products Frederiksen reserves the right to amend product spec­ ifications without prior notice. The equipment is intended for educational use and should not be used for other purposes. Returns Items may only be returned following prior agreement. Warranty Frederiksen offers a warranty of two years from the invoice date. The warranty covers manufacturing and material de­ fects. The warranty does not cover equipment that has been mistreated, poorly maintained, damaged or incorrectly assembled and equipment that has not been repaired by our workshops. IV WEIGHTSCONTENTS AND MEASURES Weights and measures 2 Weights and measures 1 - 8 Fluids, air and heat 9 - 22 Waves, sound, light and optics 23 - 54 Mechanics 55 - 74 Jens Vangklide, CEO Basic electrical equipment 75 - 98 Electrical circuits 99 - 112 Frederiksen Scientifi c A/S Viaduktvej 35 . DK­6870 Ølgod, Denmark Electric and magnetic fields 113 - 136 Atomic and nuclear physics 137 - 160 Tel. +45 7524 4966 Fax +45 7524 6282 Energy 161 - 174 [email protected] www.frederiksen.eu Geosciences 175 - 188 Opening hours: Astronomy 189 - 194 Monday­Thursday: 8.00­16.00 Laboratory fixtures and fittings 195 - 207 Friday: 8.00­15.30 1 I WEIGHTS AND MEASURES Tape measure, plastic 10 m Graduated in mm, cm and Trundle wheel metres. Glass reinforced plastic Measuring wheel with tape measure in casing with handle. winding mechanism. Indicates each revolu- Item no. 140015 tion with a click corre- sponding to 1 metre. Graduated in cm, 5 cm Ranging pole and 10 cm divisions. Length 1.7 m with red and white Item no. 142800 markings and metal tip. Item no. 140030 140010 140000 Ruler, wood Graduated in mm and cm. Wooden ruler marked horizontally, with Tape measure, plastic metal end fittings. Cross-section: 25 x 5 mm. Length: 150 cm. Graduated in mm and cm. Item no. 140500 length 50 cm Item no. 140000 Item no. 140510 length 100 cm Tape measure, metal Length: 200 cm. Graduated in mm and cm. Metal tape measure in self-retracting casing. Item no. 140010 Measuring rod, square section Length: 100 cm. Square section: 20 x 20 mm. Graduated in cm and dm. Colour printed. Item no. 141000 Folding rule Length: 200 cm. Millimetre grad- uations on both sides. Plastic. Tape measure, 20 m, steel Item no. 140530 Steel tape measure in sealed ABS casing with comfortable grip. Practi- cal belt hook. Reverse side of tape is blank. Length: 20 m. Item no. 140020 2 2 WEIGHTS AND MEASURES WEIGHTS AND MEASURES Blackboard ruler Length: 100 cm. Graduated in cm. Printed in two colours. Made from impact-resistant plastic with rubber inlay. Item no. 142010 Distance meter, electronic Simple, contactless, ultrasonic distance measurement. Can measure, for example, the length, width and height of a room and calculate the area and volume. Range 15 m. Battery not supplied. (9 V, e.g. 351010) Item no. 141520 Caliper gauge, plastic Blackboard protractor Measuring range: 0-150 Diameter: 50 cm. Graduated in degrees. Features a 50 cm rule. Made mm. Overall length: 170 mm. from impact-resistant plastic with rubber inlay. Equipped with a depth gauge Item no. 142020 and vernier scale for reading 1/20 mm increments. Item no. 144000 Caliper gauge, stain- less steel High-quality caliper gauge with a measuring range of 0-160 mm / 0-5.5 inches. With a vernier scale for reading 1/20 mm incre- ments. Depth gauge and locking mechanism. Blackboard compasses Arm length: 50 cm. Equipped with a robust chalk holder and tripod. Item no. 144020 Made from impact-resistant plastic with rubber inlay. Item no. 142050 Gun clinometer A simple angle gauge in impact-resistant plastic for measuring the height of distant objects such as houses, trees and tow- ers. Simple trigonometry formulas are used for the calculation. The necessary tables are supplied. Aim Caliper gauge, digital the "gun" at the highest Simple to use and easy to read. With zeroing button. Resolution: 0.01 point on the object and mm. Jaw length: 40 mm. Largest opening: 154 mm. Supplied in a ro- simultaneously set the an- bust case, including battery. gle, in degrees, between Item no. 144030 the horizon and the high- est point. Micrometer screw Item no. 142905 gauge Maximum measuring length: 25 mm. Precision: 0.01 mm. Equipped with a torque screw. Item no. 145050 3 3 Measuring jug, 0.5 L Plastic half-litre measuring jug with vol- ume scale. Made from impact-resist- ant plastic. Capacity: 0.5 litre. Gradu- ation: 10 ml. Item no. 146500 Measuring jug, 1 L Plastic one-litre measuring jug with vol- ume scale. Made from impact-resistant plastic. Capacity: 1.0 litre. Graduation: 10 ml. Item no. 146510 Graduated cylinder, tall Borosilicate glass with hexagonal base. The colour scale is melted into the glass surface, making it highly resistant. No. Contents Graduation Height 011020 10 ml 0.2 150 mm 011030 25 ml 0.5 170 mm 011040 50 ml 1 210 mm 011050 100 ml 1 250 mm 011060 250 ml 2 330 mm 011070 500 ml 5 360 mm 011080 1000 ml 10 450 mm 011090 2000 ml 20 570 mm Measuring spoons 6 pcs from 1/8 teaspoon to 1 tablespoon. Item no. 146805 Graduated cylinder in PMP plastic, tall Crystal-clear PMP plastic with raised scale and hexagonal base. Temperature resistant from 0° to +120° C. No. Contents Graduation Height 011810 10 ml 0.2 145 mm 011830 25 ml 0.5 170 mm 011840 50 ml 1 200 mm Weights, cubic centimetre 011850 100 ml 1 250 mm 1 g weights in the form of plastic cubes with side length of 1 cm. The cubes have holes and studs, allowing them to be combined into larger 011860 250 ml 2 315 mm units. They can only be combined into planes, not 3D figures. Supplied in a plastic bucket containing 1,000 pcs in 10 different colours. 011870 500 ml 5 360 mm Item no. 146900 011880 1000 ml 10 440 mm 4 4 WEIGHTS AND MEASURES WEIGHTS AND MEASURES Scale, pocket scale, 200 g / 0.01 g Handy pocket scale with hinged lid. Case and weighing pan included. High precision at low cost. Weighing range: 200 g Precision: 0.01 g Uses 2 x 1.5 V AAA batteries, not included Item no. 102770 Electronic laboratory scale by Kern Digital scale Quality scale from Europe's oldest weighing instrument maker. Comes with a 3-year guarantee. Powered by 9 V battery or mains adapter 5 kg/1 g (included). Dimensions: 165 x 230 x 80 mm Soehnle digital scale with a No. Model Weighing range slim design, large weighing plate and easy-to-read LCD 102930 440-47N 2000 g / 0.1 g display. Tare function. Weighing range: 0 - 5000 g. 102950 440-33N 200 g / 0.01 g Precision: 1 g Display: 4-digit LCD, 18 mm tall Supplied with 3 x 1.5 V AAA batteries. Item no. 102807 Double-pan balance on stand Sensitive balance scale on stand. Features a knife-edge bearing in hardened steel, ze- roing screws, 28 cm long nee- dle with scale, removable 120 mm diameter weighing pans, and plate for buoyancy exper- iments. The balance scale has a sensitivity of 50 mg. Scale, Ohaus, 200 g/0.1 g Dimensions: 35 x 20 x 40 cm Stackable Ohaus digital scale. Battery powered with automatic shut- Item no. 091600 off but can also be powered from mains adapter 355050. Features a calibration function. Black plastic weighing plate. Weighing range: 0 - 200 g Balance with weights Precision: 0.1 g Supplied with 3 x AA batteries.
Recommended publications
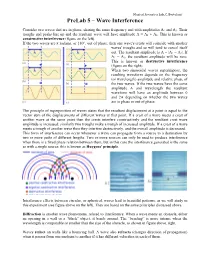
  • Prelab 5 – Wave Interference

    Prelab 5 – Wave Interference

    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
  • Quantum Interference Experiments with Large Molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger

    Quantum Interference Experiments with Large Molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger

    Quantum interference experiments with large molecules Olaf Nairz, Markus Arndt, and Anton Zeilinger Citation: American Journal of Physics 71, 319 (2003); doi: 10.1119/1.1531580 View online: http://dx.doi.org/10.1119/1.1531580 View Table of Contents: http://scitation.aip.org/content/aapt/journal/ajp/71/4?ver=pdfcov Published by the American Association of Physics Teachers Articles you may be interested in Quantum interference and control of the optical response in quantum dot molecules Appl. Phys. Lett. 103, 222101 (2013); 10.1063/1.4833239 Communication: Momentum-resolved quantum interference in optically excited surface states J. Chem. Phys. 135, 031101 (2011); 10.1063/1.3615541 Theory Of Interference Of Large Molecules AIP Conf. Proc. 899, 167 (2007); 10.1063/1.2733089 Interference with correlated photons: Five quantum mechanics experiments for undergraduates Am. J. Phys. 73, 127 (2005); 10.1119/1.1796811 Erratum: “Quantum interference experiments with large molecules” [Am. J. Phys. 71 (4), 319–325 (2003)] Am. J. Phys. 71, 1084 (2003); 10.1119/1.1603277 This article is copyrighted as indicated in the article. Reuse of AAPT content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 128.118.49.21 On: Tue, 23 Dec 2014 19:02:58 Quantum interference experiments with large molecules Olaf Nairz,a) Markus Arndt, and Anton Zeilingerb) Institut fu¨r Experimentalphysik, Universita¨t Wien, Boltzmanngasse 5, A-1090 Wien, Austria ͑Received 27 June 2002; accepted 30 October 2002͒ Wave–particle duality is frequently the first topic students encounter in elementary quantum physics. Although this phenomenon has been demonstrated with photons, electrons, neutrons, and atoms, the dual quantum character of the famous double-slit experiment can be best explained with the largest and most classical objects, which are currently the fullerene molecules.
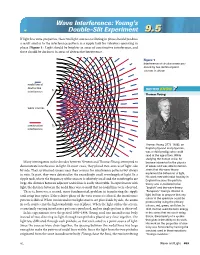
  • Wave Interference: Young's Double-Slit Experiment

    Wave Interference: Young's Double-Slit Experiment

    Wave Interference: Young’s Double-Slit Experiment 9.59.5 If light has wave properties, then two light sources oscillating in phase should produce a result similar to the interference pattern in a ripple tank for vibrators operating in phase (Figure 1). Light should be brighter in areas of constructive interference, and there should be darkness in areas of destructive interference. Figure 1 Interference of circular waves pro- duced by two identical point sources in phase nodal line of destructive S DID YOU KNOW interference 1 ?? Thomas Young wave sources constructive S2 interference Thomas Young (1773–1829), an English physicist and physician, was a child prodigy who could read at the age of two. While studying the human voice, he Many investigators in the decades between Newton and Thomas Young attempted to became interested in the physics demonstrate interference in light. In most cases, they placed two sources of light side of waves and was able to demon- by side. They scrutinized screens near their sources for interference patterns but always strate that the wave theory in vain. In part, they were defeated by the exceedingly small wavelength of light. In a explained the behaviour of light. His work met with initial hostility in ripple tank, where the frequency of the sources is relatively small and the wavelengths are England because the particle large, the distance between adjacent nodal lines is easily observable. In experiments with theory was considered to be light, the distance between the nodal lines was so small that no nodal lines were observed. “English” and the wave theory There is, however, a second, more fundamental, problem in transferring the ripple “European.” Young’s interest in tank setup into optics.
  • Diffraction Computing Systems 4 – Diffraction

    Diffraction Computing Systems 4 – Diffraction

    Dept. of Electrical Engin. & 1 Lecture 4 – Diffraction Computing Systems 4 – Diffraction ! What is each photo? What is similar for each? EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 2 Today… Computing Systems ! Today, we will mainly use wave optics to understand diffraction… ! The Photonics book relies on Fourier optics to explain this, which is too advanced for this course. Credit: Fund. Photonics – Fig. 2.3-1 Credit: Fund. Photonics – Fig. 1.0-1 ! Topics: ! This lecture has several (1) Hygens-Fresnel principle nice animations that can be (2) Single and double slit diffraction viewed in the powerpoint (3) Diffraction (‘holographic’) cards version (slide show format). Figures today are mainly from CH1 of Fund. of Photonics or wiki. EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 3 Review Computing Systems ! You could freeze a photon ! You could also freeze in time (image below) and your position and observe observe sinusoidal with sinusoidal with respect to respect to distance (kx). time (wt). ! Lastly, we can just track E, and just show peak as plane waves: E = Emax sin(wt − kx) B = Bmax sin(wt − kx) w = angular freq. (2π f, radians / s) k = angular wave number (2π / λ, radians / m) EECS 6048 – Optics for Engineers © Instructor – Prof. Jason Heikenfeld Dept. of Electrical Engin. & 4 Review Computing Systems ! Split a laser beam (coherent / plane waves) and bringing the beams back together to produce interference fringes… we will do that today also, but with an added effect of diffraction… EECS 6048 – Optics for Engineers © Instructor – Prof.
  • Genevieve Mathieson

    Genevieve Mathieson

    THOMAS YOUNG, QUAKER SCIENTIST by GENEVIEVE MATHIESON Submitted in partial fulfillment of the requirements For the degree of Master of Arts Thesis Advisor: Dr. Gillian Weiss Department of History CASE WESTERN RESERVE UNIVERSITY January, 2008 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of ______________________________________________________ candidate for the ________________________________degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. ii Table of Contents Acknowledgements............................................................................................................iii Abstract.............................................................................................................................. iv I. Introduction ..................................................................................................................... 1 II. The Life and Work of Thomas Young........................................................................... 3 Childhood and Education as a Quaker...........................................................................
  • Young and Fresnel

    Young and Fresnel

    YOUNG AND FRESNEL: A CASE-STUDY INVESTIGATING THE PROGRESS OF THE WAVE THEORY IN THE BEGINNING OF THE NINETEENTH CENTURY IN THE LIGHT OF ITS IMPLICATIONS TO THE HISTORY AND METHODOLOGY OF SCIENCE A THESIS SUBMITTED TO THE GRADUATE SCHOOL OF SOCIAL SCIENCES OF MIDDLE EAST TECHNICAL UNIVERSITY BY YEVGENIYA KULANDINA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF ARTS IN THE DEPARTMENT OF PHILOSOPHY SEPTEMBER 2013 Approval of the Graduate School of Social Sciences Prof. Dr. Meliha Altunışık Director I certify that this thesis satisfies all the requirements as a thesis for the degree of Master of Arts. Prof. Dr. Ahmet İnam Head of Department This is to certify that we have read this thesis and that in our opinion it is fully adequate, in scope and quality, as a thesis for the degree of Master of Arts. Doç. Dr. Samet Bağçe Supervisor Examining Committee Members Prof. Dr. Ahmet İnam (METU, PHIL) Doç. Dr. Samet Bağçe (METU, PHIL) Doç. Dr. Burak Yedierler (METU, PHYS) I hereby declare that all information in this document has been obtained and presented in accordance with academic rules and ethical conduct. I also declare that, as required by these rules and conduct, I have fully cited and referenced all material and results that are not original to this work. Name, Last name : Yevgeniya Kulandina Signature : iii ABSTRACT YOUNG AND FRESNEL: A CASE-STUDY INVESTIGATING THE PROGRESS OF THE WAVE THEORY IN THE BEGINNING OF THE NINETEENTH CENTURY IN THE LIGHT OF ITS IMPLICATIONS TO THE HISTORY AND METHODOLOGY OF SCIENCE Kulandina, Yevgeniya MA, Department of Philosophy Supervisor: Doç.
  • Quantum Interference Experiments with Large Molecules

    Quantum Interference Experiments with Large Molecules

    Quantum interference experiments with large molecules Olaf Nairz,a) Markus Arndt, and Anton Zeilingerb) Institut fu¨r Experimentalphysik, Universita¨t Wien, Boltzmanngasse 5, A-1090 Wien, Austria ͑Received 27 June 2002; accepted 30 October 2002͒ Wave–particle duality is frequently the first topic students encounter in elementary quantum physics. Although this phenomenon has been demonstrated with photons, electrons, neutrons, and atoms, the dual quantum character of the famous double-slit experiment can be best explained with the largest and most classical objects, which are currently the fullerene molecules. The soccer-ball-shaped carbon cages C60 are large, massive, and appealing objects for which it is clear that they must behave like particles under ordinary circumstances. We present the results of a multislit diffraction experiment with such objects to demonstrate their wave nature. The experiment serves as the basis for a discussion of several quantum concepts such as coherence, randomness, complementarity, and wave–particle duality. In particular, the effect of longitudinal ͑spectral͒ coherence can be demonstrated by a direct comparison of interferograms obtained with a thermal beam and a velocity selected beam in close analogy to the usual two-slit experiments using light. © 2003 American Association of Physics Teachers. ͓DOI: 10.1119/1.1531580͔ I. INTRODUCTION served if the disturbances in the two slits are synchronized with each other, which means that they have a well-defined At the beginning of the 20th century several important and constant phase relation, and may therefore be regarded discoveries were made leading to a set of mind-boggling as being coherent with respect to each other.
  • The Nature Of

    The Nature Of

    HOW DO WE KNOW? THE NATURE OF LIGHT BY ANDREW ROBINSON What is light? It’s puzzled some of humanity’s greatest thinkers for 2,000 years, especially since it appears to behave like waves as well as particles HAT IS LIGHT? The question in the West as Alhazen, with the Da Vinci suggested that the eye is a has fascinated scientists – and nicknames ‘Ptolemy the Second’ camera obscura – literally, ‘a darkened painters, poets, writers and and ‘The Physicist’. He noted that chamber’ – into which light rays anyone who’s ever played you cannot look at the Sun for long penetrate via a small aperture (the with a prism – since classical without great pain; and if you stare at pupil) and create an inverted image antiquity. Pythagoras, Euclid a bright object for half a minute and of an exterior scene on the back of and Ptolemy, for example, then close your eyes, a coloured image the eye (the retina). First adopted as accepted that light moved of the object floats into view. In each a term by Kepler in 1604, the camera in straight lines. But rather case, something emitted by the object obscura became the dominant model W than assuming that light rays must have entered the eye. of human vision in the 17th Century. travelled from an object to the eye, The later translation of Alhazen’s they believed the eye emitted visual Book Of Optics into Latin led to its rays, like feelers, which touched being read by, among others, artist COMPETING IDEAS the object and thereby created the Leonardo da Vinci, physicist Galileo Two theories of light, apparently sensation of sight in the mind.
  • Wave Phenomena: Ripple Tank Experiments Wave Properties

    Wave Phenomena: Ripple Tank Experiments Wave Properties

    Wave phenomena: ripple tank experiments References: PASCO Instruction Manual and Experiment Guide for Ripple Generator and Ripple Tank System G. Kuwabara, T. Hasegawa, K. Kono: Water waves in a ripple tank, Am. J. Phys. 54 (11) 1986 A.P. French: Vibrations and Waves, Norton 1971, Ch. 7 and 8 (Waves in two dimensions) R.D. Knight: Physics for Scientists and Engineers (With Modern Physics): A Strategic Approach, Pearson Education Inc. 2004 1 weight: Exercises 1-3; 2 weights: all Introduction Two-dimensional waves in water have been intensively studied in theoretical hydrodynamics. They display more complicated behaviors than acoustic or electromagnetic waves Water surface waves travel along the boundary between air and water. The restoring forces of the wave motion are surface tension and gravity. At different water depths, these two forces play different roles. The ripple tank can be used to study almost all the wave properties: reflection, refraction, interference and diffraction. In addition to this, the wave phase velocity can be investigated at different water depths and in the presence of obstacles of various shapes. Wave properties The wave speed A two-dimensional traveling wave is a disturbance of a medium, which can be expressed as a function: ψ (ax + by − vt) ω Here v is the wave speed: v = = fλ (1) k ω is the angular frequency, f is frequency, λ is the wavelength and k is the wave number. v is also called phase velocity. A non-dispersive wave has a constant v; dispersion is characterized by a dependence of v on λ. Three different regions are indicated on the dispersion curve from Figure 1: Figure 1: Dispersion curve for water waves 1 Region I: Shallow water gravity waves.
  • Ripple Tank Lab Purpose: Use a Ripple Tank to Investigate Wave Properties of Reflection, Refraction and Diffraction

    Ripple Tank Lab Purpose: Use a Ripple Tank to Investigate Wave Properties of Reflection, Refraction and Diffraction

    Ripple Tank Lab Purpose: Use a ripple tank to investigate wave properties of reflection, refraction and diffraction. A ripple tank provides an ideal medium for observing the behavior of waves. The ripple tank projects images of waves in the water onto a screen below the tank. Just as you have probably observed in a swimming pool, light shining through water waves is seen as a pattern of bright lines and dark lines separated by gray areas. The water acts as a series of lenses, bending the light that passes through it. In the ripple tank, the wave crests focus light from the light source and produce bright lines on the paper. Troughs in the ripple tank waves cause the light to diverge and produce dark lines (Areas of no disturbance). In this experiment you will investigate a number of wave properties, including reflection, refraction and diffraction. The law of reflection states that the angle of incidence equals the angle of reflection. Waves undergoing a change in speed and direction as they pass from one medium to another are demonstrating refraction. The spreading of waves around the edge of a barrier or through a narrow opening exemplifies diffraction. You will generate waves in a ripple tank and observe the effects on wave behavior of different types of ‘media interfaces’. Materials: ripple tank light source dowel rod 2 paraffin blocks protractor & ruler a few pennies meter stick flat glass plate, angle cut white paper Procedure: Make sure you have the white reflector sheet under the legs of the tank. Check the depth of water in your tank at all four corners, and make sure the tank is level.
  • Alternative Setup for Estimating Reliable Frequency Values in a Ripple Tank

    Alternative Setup for Estimating Reliable Frequency Values in a Ripple Tank

    Alternative setup for estimating reliable frequency values in a ripple tank Documento de Discusión CIUP DD1701 Enero, 2017 Ana Luna Profesora e investigadora del CIUP [email protected] Las opiniones expresadas en este documento son de exclusiva responsabilidad del autor y no expresan necesariamente aquellas del Centro de Investigación de la Universidad del Pacífico o de Universidad misma. The opinions expressed here in are those of the authors and do not necessarily reflect those of the Research Center of the Universidad del Pacifico or the University itself. Alternative setup for estimating reliable frequency values in a ripple tank Ana Luna+, Miguel Nu nez-del-Prado˜ Jose´ Luj an,´ Luis Mantilla Garc ´ıa, Daniel Malca Department of Engineering Colegio Peruano Brit anico´ Universidad del Pac ´ıfico, Lima - Per u´ Lima - Per u´ {ae.lunaa, m.nunezdelpradoc}@up.edu.pe {jlujanmontufar, luiscalolo10x, dmalcaruiz }@gmail.com Abstract—In this paper, we introduce an innovative, low- labs. Indirect and reliable oscillation frequency measurements cost and easy experimental setup to be used in a traditional were computed for estimating the propagation velocity of a ripple tank when a frequency generator is unavailable. This mechanical wave in different media. configuration was carried out by undergraduate students. The current project allowed them to experiment and to study the relationship between the wavelength and the oscillation period The goal of this paper goes beyond the relationship study of a mechanical wave, among other things. Under this setup, between two physical magnitudes. On the one hand, the students could evaluate the mechanism not only qualitative but design and presentation of a reliable experimental device, also in a quantitative fashion with a high degree of confidence.
  • Do-It-Yourself Sedimentology

    Do-It-Yourself Sedimentology

    Nature Vol. 260 April 1 1976 463 reviews• A (highly) intelligent school leaver index. References are mostly to mono­ about to take up an appointment as graphs and reviews, rather than to an X-ray crystallographer in a bio­ Desert island original papers The illustrations are chemical laboratory and wrecked on plentiful and informative, although a desert island on his way, would find crystallography more modern X-ray photographs of the present volume invaluable in equip­ biological materials might have been ping him for his new post by the time chosen. The text seems reasonably free of his rescue. Dr Sherwood takes the U. W. Arndt of errors and misprints. It is a little reader in a methodical way through strange to find within the same covers all the necessary steps to the solution Crystals, X Rays and Proteins. By an illustration of wave interference in of an unknown crystal structure. He Dennis Sherwood. Pp. xxii + 702. a ripple tank and a derivation of the starts with an explanation of the fun­ (Longman: London, January 1976.) Harker-Kaspar inequalities, but the damentals of crystallography, of wave £12.50. author has fulfilled his stated intention motion, of diffraction and Fourier of saying something of use for every transform theory and develops the nec­ class of reader in every section. Al­ essary mathematical methods on the organic structure. though the coverage of the theory of way. He then deals with the theory The presentation is clear and fairly X -ray crystallography is fairly com­ and practice of crystallographic struc­ mathematical although it is a little plete the reader will have to look ture determination-intensity measure­ doubtful whether it could be followed elsewhere for a description of experi­ ment, extinction, Patterson methods, in its entirety by a reader who had mental methods.