Surrogate Assisted Semi-Supervised Inference for High Dimensional Risk Prediction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Kūnqǔ in Practice: a Case Study
KŪNQǓ IN PRACTICE: A CASE STUDY A DISSERTATION SUBMITTED TO THE GRADUATE DIVISION OF THE UNIVERSITY OF HAWAI‘I AT MĀNOA IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY IN THEATRE OCTOBER 2019 By Ju-Hua Wei Dissertation Committee: Elizabeth A. Wichmann-Walczak, Chairperson Lurana Donnels O’Malley Kirstin A. Pauka Cathryn H. Clayton Shana J. Brown Keywords: kunqu, kunju, opera, performance, text, music, creation, practice, Wei Liangfu © 2019, Ju-Hua Wei ii ACKNOWLEDGEMENTS I wish to express my gratitude to the individuals who helped me in completion of my dissertation and on my journey of exploring the world of theatre and music: Shén Fúqìng 沈福庆 (1933-2013), for being a thoughtful teacher and a father figure. He taught me the spirit of jīngjù and demonstrated the ultimate fine art of jīngjù music and singing. He was an inspiration to all of us who learned from him. And to his spouse, Zhāng Qìnglán 张庆兰, for her motherly love during my jīngjù research in Nánjīng 南京. Sūn Jiàn’ān 孙建安, for being a great mentor to me, bringing me along on all occasions, introducing me to the production team which initiated the project for my dissertation, attending the kūnqǔ performances in which he was involved, meeting his kūnqǔ expert friends, listening to his music lessons, and more; anything which he thought might benefit my understanding of all aspects of kūnqǔ. I am grateful for all his support and his profound knowledge of kūnqǔ music composition. Wichmann-Walczak, Elizabeth, for her years of endeavor producing jīngjù productions in the US. -
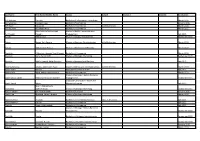
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation A/L Krishnan Thiinash Bachelor of Information Technology March 2015 A/L Selvaraju Theeban Raju Bachelor of Commerce January 2015 A/P Balan Durgarani Bachelor of Commerce with Distinction March 2015 A/P Rajaram Koushalya Priya Bachelor of Commerce March 2015 Hiba Mohsin Mohammed Master of Health Leadership and Aal-Yaseen Hussein Management July 2015 Aamer Muhammad Master of Quality Management September 2015 Abbas Hanaa Safy Seyam Master of Business Administration with Distinction March 2015 Abbasi Muhammad Hamza Master of International Business March 2015 Abdallah AlMustafa Hussein Saad Elsayed Bachelor of Commerce March 2015 Abdallah Asma Samir Lutfi Master of Strategic Marketing September 2015 Abdallah Moh'd Jawdat Abdel Rahman Master of International Business July 2015 AbdelAaty Mosa Amany Abdelkader Saad Master of Media and Communications with Distinction March 2015 Abdel-Karim Mervat Graduate Diploma in TESOL July 2015 Abdelmalik Mark Maher Abdelmesseh Bachelor of Commerce March 2015 Master of Strategic Human Resource Abdelrahman Abdo Mohammed Talat Abdelziz Management September 2015 Graduate Certificate in Health and Abdel-Sayed Mario Physical Education July 2015 Sherif Ahmed Fathy AbdRabou Abdelmohsen Master of Strategic Marketing September 2015 Abdul Hakeem Siti Fatimah Binte Bachelor of Science January 2015 Abdul Haq Shaddad Yousef Ibrahim Master of Strategic Marketing March 2015 Abdul Rahman Al Jabier Bachelor of Engineering Honours Class II, Division 1 -

Digesting Anomalies: an Investment Approach
Digesting Anomalies: An Investment Approach Kewei Hou The Ohio State University and China Academy of Financial Research Chen Xue University of Cincinnati Lu Zhang The Ohio State University and National Bureau of Economic Research An empirical q-factor model consisting of the market factor, a size factor, an investment factor, and a profitability factor largely summarizes the cross section of average stock returns. A comprehensive examination of nearly 80 anomalies reveals that about one-half of the anomalies are insignificant in the broad cross section. More importantly, with a few exceptions, the q-factor model’s performance is at least comparable to, and in many cases better than that of the Fama-French (1993) 3-factor model and the Carhart (1997) 4-factor model in capturing the remaining significant anomalies. (JEL G12, G14) In a highly influential article, Fama and French (1996) show that, except for momentum, their 3-factor model, which consists of the market factor, a factor based on market equity (small-minus-big, SMB), and a factor based on book- to-market equity (high-minus-low, HML), summarizes the cross section of average stock returns as of the mid-1990s. Over the past 2 decades, however, it has become clear that the Fama-French model fails to account for a wide array of asset pricing anomalies.1 We thank Roger Loh, René Stulz, Mike Weisbach, Ingrid Werner, Jialin Yu, and other seminar participants at the 2013 China International Conference in Finance and the Ohio State University for helpful comments. Geert Bekaert (the editor) and three anonymous referees deserve special thanks. -

The Later Han Empire (25-220CE) & Its Northwestern Frontier
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations 2012 Dynamics of Disintegration: The Later Han Empire (25-220CE) & Its Northwestern Frontier Wai Kit Wicky Tse University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Asian History Commons, Asian Studies Commons, and the Military History Commons Recommended Citation Tse, Wai Kit Wicky, "Dynamics of Disintegration: The Later Han Empire (25-220CE) & Its Northwestern Frontier" (2012). Publicly Accessible Penn Dissertations. 589. https://repository.upenn.edu/edissertations/589 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/589 For more information, please contact [email protected]. Dynamics of Disintegration: The Later Han Empire (25-220CE) & Its Northwestern Frontier Abstract As a frontier region of the Qin-Han (221BCE-220CE) empire, the northwest was a new territory to the Chinese realm. Until the Later Han (25-220CE) times, some portions of the northwestern region had only been part of imperial soil for one hundred years. Its coalescence into the Chinese empire was a product of long-term expansion and conquest, which arguably defined the egionr 's military nature. Furthermore, in the harsh natural environment of the region, only tough people could survive, and unsurprisingly, the region fostered vigorous warriors. Mixed culture and multi-ethnicity featured prominently in this highly militarized frontier society, which contrasted sharply with the imperial center that promoted unified cultural values and stood in the way of a greater degree of transregional integration. As this project shows, it was the northwesterners who went through a process of political peripheralization during the Later Han times played a harbinger role of the disintegration of the empire and eventually led to the breakdown of the early imperial system in Chinese history. -

MIMO-NOMA Networks Relying on Reconfigurable Intelligent Surface
1 MIMO-NOMA Networks Relying on Reconfigurable Intelligent Surface: A Signal Cancellation Based Design Tianwei Hou, Student Member, IEEE, Yuanwei Liu, Senior Member, IEEE, Zhengyu Song, Xin Sun, and Yue Chen, Senior Member, IEEE, Abstract Reconfigurable intelligent surface (RIS) technique stands as a promising signal enhancement or signal cancellation technique for next generation networks. We design a novel passive beamforming weight at RISs in a multiple-input multiple-output (MIMO) non-orthogonal multiple access (NOMA) network for simultaneously serving paired users, where a signal cancellation based (SCB) design is employed. In order to implement the proposed SCB design, we first evaluate the minimal required number of RISs in both the diffuse scattering and anomalous reflector scenarios. Then, new channel statistics are derived for characterizing the effective channel gains. In order to evaluate the network’s performance, we derive the closed-form expressions both for the outage probability (OP) and for the ergodic rate (ER). The diversity orders as well as the high-signal-to-noise (SNR) slopes are derived for engineering insights. The network’s performance of a finite resolution design has been evaluated. Our analytical results demonstrate that: i) the inter-cluster interference can be eliminated with the aid of arXiv:2003.02117v1 [cs.IT] 4 Mar 2020 large number of RIS elements; ii) the line-of-sight of the BS-RIS and RIS-user links are required for the diffuse scattering scenario, whereas the LoS links are not compulsory for the anomalous reflector scenario. Index Terms This work is supported by the National Natural Science Foundation of China under Grant 61901027. -

Evaluation of Ballast Behavior Under Different Tie Support Conditions Using Discrete Element Modeling
EVALUATION OF BALLAST BEHAVIOR UNDER DIFFERENT TIE SUPPORT CONDITIONS USING DISCRETE ELEMENT MODELING Wenting Hou1 Ph.D. Student, Graduate Research Assistant Tel: (217) 550-5686; Email: [email protected] Bin Feng1 Ph.D. Student, Graduate Research Assistant Tel: (217) 721-4381; Email: [email protected] Wei Li2 Ph.D. Student, Graduate Research Assistant Tel: (217) 305-0023; Email: [email protected] Erol Tutumluer1 Ph.D., Professor (Corresponding Author) Paul F. Kent Endowed Faculty Scholar Tel: (217) 333-8637; Email: [email protected] 1Department of Civil and Environmental Engineering University of Illinois at Urbana-Champaign 205 North Mathews, Urbana, Illinois 61801 2Zhejiang University, Hangzhou, China Word Count: 4,639 words + 1 Tables (1*250) + 8 Figures (8*250) = 6,889 TRR Paper No: 18-04833 Submission Date: March 15, 2018 2 Hou, Feng, Li, and Tutumluer ABSTRACT This paper presents findings of a railroad ballast study using the Discrete Element Method (DEM) focused on mesoscale performance modeling of ballast layer under different tie support conditions. The simulation assembles ballast gradation that met the requirements of both AREMA No. 3 and No. 4A specifications with polyhedral particle shapes created similar to the field collected ballast samples. A full-track model was generated as a basic model, upon which five different support conditions were studied in the DEM simulation. Static rail seat loads of 10- kips were applied until the DEM model became stable. The pressure distribution along tie-ballast interface predicted by DEM simulations was in good agreement with previously published results backcalculated from laboratory testing. Static rail seat loads of 20 kips were then applied in the calibrated DEM model to evaluate in-track performance. -

A Study of the Mystery of Zeng: Recent Perspectives
Research Article Glob J Arch & Anthropol Volume 1 Issue 3 - May 2017 Copyright © All rights are reserved by Beichen Chen A Study of the Mystery of Zeng: Recent Perspectives Beichen Chen* University of Oxford, UK Submission: February 20, 2017; Published: June 15, 2017 *Corresponding author: Beichen Chen, University of Oxford, Merton College, Oxford, OX1 4JD, England, UK, Tel: ; Email: Abstract The study of the Zeng 曾 state known from palaeographic sources is often intertwined with the state of Sui 隨 known from the transmitted texts. A newly excavated Zeng cemetery at Wenfengta 文峰塔, Hubei 湖 Suizhou 隨州 extends our understanding of the state itself in many yielded a set of large musical bells with long narrative inscriptions, which suggest that state of Zeng had provided crucial assistance to a Chu kingrespects, during such the as war its lineagebetween history, the states bronze of Chu casting and Wutraditions, 吳. As some ritual scholars and burial suggest, practice, this and issue so mayon. One be correlated tomb at ruler’s to the level text -in Wenfengta Zuo Zhuan M1- 左 傳 (Ding 4 定公四年), which records that it was the state of Sui who saved a Chu king from the Wu invaders. Such an argument brings again 曾國之謎’, Sui refer to the same state’. The current paper aims to have a brief review of this debate, and further discuss the perspectives of the debaters basedinto spotlight on the newly the ‘age-old’ excavated debate materials. of the ‘Mystery of Zeng or more specifically, the debate about ‘whether or not the Zeng and the Keywords: The mystery of zeng; Zeng and sui; Wenfengta Introduction regional powers to the north of the Han River 漢水 , [2] dated from no later than the late Western Zhou to the early Warring The states of Zeng and Sui are considered as two mysterious States period [3]. -

Zhenzhong Zeng School of Environmental Science And
Zhenzhong Zeng School of Environmental Science and Engineering, Southern University of Science and Technology [email protected] | https://scholar.google.com/citations?user=GsM4YKQAAAAJ&hl=en CURRENT POSITION Associate Professor, Southern University of Science and Technology, since 2019.09.04 PROFESSIONAL EXPERIENCE Postdoctoral Research Associate, Princeton University, 2016-2019 (Mentor: Dr. Eric F. Wood) EDUCATION Ph.D. in Physical Geography, Peking University, 2011-2016 (Supervisor: Dr. Shilong Piao) B.S. in Geography Science, Sun Yat-Sen University, 2007-2011 RESEARCH INTERESTS Global change and the earth system Biosphere-atmosphere interactions Terrestrial hydrology Water and agriculture resources Climate change and its impacts, with a focus on China and the tropics AWARDS & HONORS 2019 Shenzhen High Level Professionals – National Leading Talents 2018 “China Agricultural Science Major Progress” - Impacts of climate warming on global crop yields and feedbacks of vegetation growth change on global climate, Chinese Academy of Agricultural Sciences 2016 Outstanding Graduate of Peking University 2013 – 2016 Presidential (Peking University) Scholarship; 2014 – 2015 Peking University PhD Projects Award; 2013 – 2014 Peking University "Innovation Award"; 2013 – 2014 National Scholarship; 2012 – 2013 Guanghua Scholarship; 2011 – 2012 National Scholarship; 2011 – 2012 Founder Scholarship 2011 Outstanding Graduate of Sun Yat-Sen University 2009 National Undergraduate Mathematical Contest in Modeling (Provincial Award); 2009 – 2010 National Scholarship; 2008 – 2009 National Scholarship; 2007 – 2008 Guanghua Scholarship PUBLICATION LIST 1. Liu, X., Huang, Y., Xu, X., Li, X., Li, X.*, Ciais, P., Lin, P., Gong, K., Ziegler, A. D., Chen, A., Gong, P., Chen, J., Hu, G., Chen, Y., Wang, S., Wu, Q., Huang, K., Estes, L. & Zeng, Z.* High spatiotemporal resolution mapping of global urban change from 1985 to 2015. -

Rethinking Chinese Kinship in the Han and the Six Dynasties: a Preliminary Observation
part 1 volume xxiii • academia sinica • taiwan • 2010 INSTITUTE OF HISTORY AND PHILOLOGY third series asia major • third series • volume xxiii • part 1 • 2010 rethinking chinese kinship hou xudong 侯旭東 translated and edited by howard l. goodman Rethinking Chinese Kinship in the Han and the Six Dynasties: A Preliminary Observation n the eyes of most sinologists and Chinese scholars generally, even I most everyday Chinese, the dominant social organization during imperial China was patrilineal descent groups (often called PDG; and in Chinese usually “zongzu 宗族”),1 whatever the regional differences between south and north China. Particularly after the systematization of Maurice Freedman in the 1950s and 1960s, this view, as a stereo- type concerning China, has greatly affected the West’s understanding of the Chinese past. Meanwhile, most Chinese also wear the same PDG- focused glasses, even if the background from which they arrive at this view differs from the West’s. Recently like Patricia B. Ebrey, P. Steven Sangren, and James L. Watson have tried to challenge the prevailing idea from diverse perspectives.2 Some have proven that PDG proper did not appear until the Song era (in other words, about the eleventh century). Although they have confirmed that PDG was a somewhat later institution, the actual underlying view remains the same as before. Ebrey and Watson, for example, indicate: “Many basic kinship prin- ciples and practices continued with only minor changes from the Han through the Ch’ing dynasties.”3 In other words, they assume a certain continuity of paternally linked descent before and after the Song, and insist that the Chinese possessed such a tradition at least from the Han 1 This article will use both “PDG” and “zongzu” rather than try to formalize one term or one English translation. -

Immigration and Firm Productivity
Immigration and Firm Productivity: Evidence from the Canadian Employer-Employee Dynamics Database Feng Hou,* Wulong Gu and Garnett Picot [email protected] Statistics Canada March, 2018 Abstract Previous studies on the impact of immigration on productivity in developed countries remain inconclusive, and most analyses are abstracted from firms where production actually takes place. This study examines the empirical relationship between immigration and firm-level productivity in Canada. It uses the Canadian Employer-Employee Dynamics Database that tracks firms over time and matches firms with their employees. The main analyses are based on the relationship between the changes in the share of immigrants in a firm and firm productivity, whereas the change is measured alternatively over one-year, five-year, and ten-year intervals. The study includes only firms with at least 20 employees in a given year in order to derive relatively reliable firm-level measures. The results show that the positive association between changes in the share of immigrants and firm productivity was stronger over a longer period of changes. The overall positive association was small. Furthermore, firm productivity growth was more strongly associated with changes in the share of recent immigrants (relative to established immigrants), immigrants who intended to work in non-high skilled occupations (relative to immigrants who intended to work high-skilled occupations), and immigrants who intended to work in non-STEM occupations (relative to immigrants who intended to work in STEM occupations). These patterns held mostly in technology-intensive or knowledge-based industries. The implications of these results are discussed. 1 1. Introduction The effect of immigration on the receiving country’s economy is an issue of intense policy and academic discussions. -

Surname Methodology in Defining Ethnic Populations : Chinese
Surname Methodology in Defining Ethnic Populations: Chinese Canadians Ethnic Surveillance Series #1 August, 2005 Surveillance Methodology, Health Surveillance, Public Health Division, Alberta Health and Wellness For more information contact: Health Surveillance Alberta Health and Wellness 24th Floor, TELUS Plaza North Tower P.O. Box 1360 10025 Jasper Avenue, STN Main Edmonton, Alberta T5J 2N3 Phone: (780) 427-4518 Fax: (780) 427-1470 Website: www.health.gov.ab.ca ISBN (on-line PDF version): 0-7785-3471-5 Acknowledgements This report was written by Dr. Hude Quan, University of Calgary Dr. Donald Schopflocher, Alberta Health and Wellness Dr. Fu-Lin Wang, Alberta Health and Wellness (Authors are ordered by alphabetic order of surname). The authors gratefully acknowledge the surname review panel members of Thu Ha Nguyen and Siu Yu, and valuable comments from Yan Jin and Shaun Malo of Alberta Health & Wellness. They also thank Dr. Carolyn De Coster who helped with the writing and editing of the report. Thanks to Fraser Noseworthy for assisting with the cover page design. i EXECUTIVE SUMMARY A Chinese surname list to define Chinese ethnicity was developed through literature review, a panel review, and a telephone survey of a randomly selected sample in Calgary. It was validated with the Canadian Community Health Survey (CCHS). Results show that the proportion who self-reported as Chinese has high agreement with the proportion identified by the surname list in the CCHS. The surname list was applied to the Alberta Health Insurance Plan registry database to define the Chinese ethnic population, and to the Vital Statistics Death Registry to assess the Chinese ethnic population mortality in Alberta. -

Short- and Long-Horizon Behavioral Factors
Short- and Long-Horizon Behavioral Factors Kent Daniel, David Hirshleifer and Lin Sun∗ March 1, 2018 Abstract Recent theories suggest that both risk and mispricing are associated with commonality in security returns, and that the loadings on characteristic-based factors can be used to predict future returns. We supplement the market factor with two mispricing factors which capture long- and short-horizon mispricing. Our financing factor is based on evidence that managers exploit long-horizon mispricing by issuing or repurchasing equity. Our earnings surprise factor, which is motivated by evidence of limited attention and short-horizon mispricing, captures short-horizon anomalies. Our three-factor risk-and-behavioral model outperforms both traditional and other prominent factor models in explaining a large set of return anomalies. ∗Daniel: Columbia Business School and NBER; Hirshleifer: Merage School of Business, UC Irvine and NBER; Sun: Florida State University. We appreciate helpful comments from Jawad Addoum (FIRS discussant), Chong Huang, Danling Jiang, Frank Weikai Li (CICF discussant), Christian Lundblad (Miami Behavioral Finance Conference discussant), Anthony Lynch (SFS Cavalcade discussant), Stefan Nagel, Christopher Schwarz, Robert Stambaugh (AFA discussant), Zheng Sun, Siew Hong Teoh, Yi Zhang (FMA discussant), Lu Zheng, seminar participants at UC Irvine, University of Nebraska, Lincoln, Florida State University, Arizona State University, and from participants in the FIRS meeting at Quebec City, Canada, the FMA meeting at Nashville,