·11M~Mw111¡•·
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Journal Abbreviations
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). not previously listed ⇤ The abbreviation is followed by the complete title, the place of publication journal indexed cover-to-cover § and other pertinent information. † monographic series Update date: July 1, 2016 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN Acta Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. § 1619-4500. ISSN 0236-5294. 29o Col´oq. Bras. Mat. 29o Col´oquio Brasileiro de Matem´atica. [29th Brazilian Acta Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue † § Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN o o † 30 Col´oq. Bras. Mat. 30 Col´oquio Brasileiro de Matem´atica. [30th Brazilian 1003-3998. ⇤ Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. Acta Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English § Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. † Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Acta Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). § Springer, Berlin. ISSN 1439-8516. † Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. Abh. Akad. Wiss. G¨ottingen Neue Folge Abhandlungen der Akademie der Acta Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. Chinese Series. † § Wissenschaften zu G¨ottingen. Neue Folge. [Papers of the Academy of Sciences Chinese Math. Soc., Acta Math. Sinica Ed. Comm., Beijing. ISSN 0583-1431. -

Matematické Ćasopisy Vedené V Databázi SCOPUS
Matematické časopisy vedené v databázi SCOPUS (stav k 21. 1. 2009) Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg Abstract and Applied Analysis ACM Computing Surveys ACM Transactions on Algorithms ACM Transactions on Computational Logic ACM Transactions on Computer Systems ACM Transactions on Speech and Language Processing Acta Applicandae Mathematicae Acta Arithmetica Acta Mathematica Acta Mathematica Academiae Paedagogicae Nyiregyhaziensis Acta Mathematica Hungarica Acta Mathematica Scientia Acta Mathematica Sinica, English Series Acta Mathematica Universitatis Comenianae Acta Mathematicae Applicatae Sinica Acta Mathematicae Applicatae Sinica, English Series Acta Mechanica Sinica Acta Numerica Advanced Nonlinear Studies Advanced Studies in Contemporary Mathematics (Kyungshang) Advanced Studies in Theoretical Physics Advances in Applied Clifford Algebras Advances in Applied Mathematics Advances in Applied Probability Advances in Computational Mathematics Advances in Difference Equations Advances in Geometry Advances in Mathematics Advances in modelling and analysis. A, general mathematical and computer tools Advances in Nonlinear Variational Inequalities Advances in Theoretical and Mathematical Physics Aequationes Mathematicae Algebra and Logic Algebra Colloquium Algebra Universalis Algebras and Representation Theory Algorithms for Molecular Biology American Journal of Mathematical and Management Sciences American Journal of Mathematics American Mathematical Monthly Analysis in Theory and Applications Analysis Mathematica -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed E available electronically The abbreviation is followed by the complete title, the place of publication § journal reviewed cover-to-cover V videocassette series and other pertinent information. † monographic series ¶ bibliographic journal E 4OR 4OR. Quarterly Journal of the Belgian, French and Italian Operations Research ISSN 1211-4774. Societies. Springer, Berlin. ISSN 1619-4500. §Acta Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Wuli † 19o Col´oq. Bras. Mat. 19o Col´oquio Brasileiro de Matem´atica. [19th Brazilian Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. (See also Acta Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. Math.Sci.Ser.BEngl.Ed.) ISSN 1003-3998. † 24o Col´oq. Bras. Mat. 24o Col´oquio Brasileiro de Matem´atica. [24th Brazilian §ActaMath.Sci.Ser.BEngl.Ed. Acta Mathematica Scientia. Series B. English Edition. Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. Science Press, Beijing. (See also Acta Math. Sci. Ser. A Chin. Ed.) ISSN 0252- † 25o Col´oq. Bras. Mat. 25o Col´oquio Brasileiro de Matem´atica. [25th Brazilian 9602. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. § E Acta Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). Springer, † Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. Estonian Heidelberg. ISSN 1439-8516. Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. § E Acta Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. Chinese Series. Chinese Math. Abh. Braunschw. Wiss. Ges. Abhandlungen der Braunschweigischen Wissenschaftlichen Soc., Acta Math. -

SCIENCE CITATION INDEX EXPANDED - JOURNAL LIST Total Journals: 8631
SCIENCE CITATION INDEX EXPANDED - JOURNAL LIST Total journals: 8631 1. 4OR-A QUARTERLY JOURNAL OF OPERATIONS RESEARCH 2. AAPG BULLETIN 3. AAPS JOURNAL 4. AAPS PHARMSCITECH 5. AATCC REVIEW 6. ABDOMINAL IMAGING 7. ABHANDLUNGEN AUS DEM MATHEMATISCHEN SEMINAR DER UNIVERSITAT HAMBURG 8. ABSTRACT AND APPLIED ANALYSIS 9. ABSTRACTS OF PAPERS OF THE AMERICAN CHEMICAL SOCIETY 10. ACADEMIC EMERGENCY MEDICINE 11. ACADEMIC MEDICINE 12. ACADEMIC PEDIATRICS 13. ACADEMIC RADIOLOGY 14. ACCOUNTABILITY IN RESEARCH-POLICIES AND QUALITY ASSURANCE 15. ACCOUNTS OF CHEMICAL RESEARCH 16. ACCREDITATION AND QUALITY ASSURANCE 17. ACI MATERIALS JOURNAL 18. ACI STRUCTURAL JOURNAL 19. ACM COMPUTING SURVEYS 20. ACM JOURNAL ON EMERGING TECHNOLOGIES IN COMPUTING SYSTEMS 21. ACM SIGCOMM COMPUTER COMMUNICATION REVIEW 22. ACM SIGPLAN NOTICES 23. ACM TRANSACTIONS ON ALGORITHMS 24. ACM TRANSACTIONS ON APPLIED PERCEPTION 25. ACM TRANSACTIONS ON ARCHITECTURE AND CODE OPTIMIZATION 26. ACM TRANSACTIONS ON AUTONOMOUS AND ADAPTIVE SYSTEMS 27. ACM TRANSACTIONS ON COMPUTATIONAL LOGIC 28. ACM TRANSACTIONS ON COMPUTER SYSTEMS 29. ACM TRANSACTIONS ON COMPUTER-HUMAN INTERACTION 30. ACM TRANSACTIONS ON DATABASE SYSTEMS 31. ACM TRANSACTIONS ON DESIGN AUTOMATION OF ELECTRONIC SYSTEMS 32. ACM TRANSACTIONS ON EMBEDDED COMPUTING SYSTEMS 33. ACM TRANSACTIONS ON GRAPHICS 34. ACM TRANSACTIONS ON INFORMATION AND SYSTEM SECURITY 35. ACM TRANSACTIONS ON INFORMATION SYSTEMS 36. ACM TRANSACTIONS ON INTELLIGENT SYSTEMS AND TECHNOLOGY 37. ACM TRANSACTIONS ON INTERNET TECHNOLOGY 38. ACM TRANSACTIONS ON KNOWLEDGE DISCOVERY FROM DATA 39. ACM TRANSACTIONS ON MATHEMATICAL SOFTWARE 40. ACM TRANSACTIONS ON MODELING AND COMPUTER SIMULATION 41. ACM TRANSACTIONS ON MULTIMEDIA COMPUTING COMMUNICATIONS AND APPLICATIONS 42. ACM TRANSACTIONS ON PROGRAMMING LANGUAGES AND SYSTEMS 43. ACM TRANSACTIONS ON RECONFIGURABLE TECHNOLOGY AND SYSTEMS 44. -

List of Mathematics Impact Factor Journals Indexed in ISI Web of Science (JCR SCI, 2016)
List of Mathematics Impact Factor Journals Indexed in ISI Web of Science (JCR SCI, 2016) Compiled by: Arslan Sheikh In Charge Reference & Research Section Library Information Services COMSATS Institute of Information Technology Park Road, Islamabad-Pakistan. Cell No +92-0321-9423071 [email protected] Rank Journal Title ISSN Impact Factor 1 ACTA NUMERICA 0962-4929 6.250 2 SIAM REVIEW 0036-1445 4.897 3 JOURNAL OF THE AMERICAN MATHEMATICAL SOCIETY 0894-0347 4.692 4 Nonlinear Analysis-Hybrid Systems 1751-570X 3.963 5 ANNALS OF MATHEMATICS 0003-486X 3.921 6 COMMUNICATIONS ON PURE AND APPLIED MATHEMATICS 0010-3640 3.793 7 INTERNATIONAL JOURNAL OF ROBUST AND NONLINEAR CONTROL 1049-8923 3.393 8 ACM TRANSACTIONS ON MATHEMATICAL SOFTWARE 0098-3500 3.275 9 Publications Mathematiques de l IHES 0073-8301 3.182 10 INVENTIONES MATHEMATICAE 0020-9910 2.946 11 MATHEMATICAL MODELS & METHODS IN APPLIED SCIENCES 0218-2025 2.860 12 Advances in Nonlinear Analysis 2191-9496 2.844 13 FOUNDATIONS OF COMPUTATIONAL MATHEMATICS 1615-3375 2.829 14 Communications in Nonlinear Science and Numerical Simulation 1007-5704 2.784 15 FUZZY SETS AND SYSTEMS 0165-0114 2.718 16 APPLIED AND COMPUTATIONAL HARMONIC ANALYSIS 1063-5203 2.634 17 SIAM Journal on Imaging Sciences 1936-4954 2.485 18 ANNALES DE L INSTITUT HENRI POINCARE-ANALYSE NON LINEAIRE 0294-1449 2.450 19 ACTA MATHEMATICA 0001-5962 2.448 20 MATHEMATICAL PROGRAMMING 0025-5610 2.446 21 ARCHIVE FOR RATIONAL MECHANICS AND ANALYSIS 0003-9527 2.392 22 CHAOS 1054-1500 2.283 23 APPLIED MATHEMATICS LETTERS 0893-9659 -

Scopus Indexed Journals, Updated List 2018
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/320410854 Scopus indexed journals, updated list 2018 Poster · October 2017 DOI: 10.13140/RG.2.2.34648.60168 CITATIONS READS 0 351,409 1 author: Ahmad Rayan Zarqa University 73 PUBLICATIONS 171 CITATIONS SEE PROFILE Some of the authors of this publication are also working on these related projects: A Cross Sectional Study To Evaluate Awareness Regarding Non-Cytotoxic Medication Extravasation Amongst Registered Nurses Representing A Tertiary Health Care Institution In Western Saudi Arabi View project I am working on mental health at school based View project All content following this page was uploaded by Ahmad Rayan on 15 October 2017. The user has requested enhancement of the downloaded file. Source Title Print-ISSN E-ISSN Open Acces status, i.e., registered in DOAJ and/or ROAD. Status March 2016 2D Materials 20531583 3 Biotech 2190572X 21905738 DOAJ/ROAD Open Access 3D Research 20926731 3L: Language, Linguistics, Literature 01285157 DOAJ/ROAD Open Access 4OR 16194500 16142411 A & A case reports 23257237 A + U-Architecture and Urbanism 03899160 A Contrario. Revue interdisciplinaire de sciences sociales 16607880 a/b: Auto/Biography Studies 21517290 A|Z ITU Journal of Faculty of Architecture 13028324 AAA, Arbeiten aus Anglistik und Amerikanistik 01715410 AAC: Augmentative and Alternative Communication 07434618 14773848 AACL Bioflux 18448143 18449166 DOAJ/ROAD Open Access AACN Advanced Critical Care 15597768 AANA Journal 00946354 -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed The abbreviation is followed by the complete title, the place of publication x journal indexed cover-to-cover and other pertinent information. y monographic series Update date: January 30, 2018 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN xActa Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English 1619-4500. Series. Springer, Heidelberg. ISSN 0168-9673. y 30o Col´oq.Bras. Mat. 30o Col´oquioBrasileiro de Matem´atica. [30th Brazilian xActa Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. ISSN 0236-5294. y Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. xActa Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN y Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. 1003-3998. y Abh. Akad. Wiss. G¨ottingenNeue Folge Abhandlungen der Akademie der xActa Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English Wissenschaften zu G¨ottingen.Neue Folge. [Papers of the Academy of Sciences Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. in G¨ottingen.New Series] De Gruyter/Akademie Forschung, Berlin. ISSN 0930- xActa Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). 4304. Springer, Berlin. ISSN 1439-8516. y Abh. Akad. Wiss. Hamburg Abhandlungen der Akademie der Wissenschaften xActa Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. -

Kazimierz Kuratowski (Warsaw)
Kazimierz Kuratowski (Warsaw) THE PAST AND THE PRESENT OF THE POLISH SCHOOL OF MATHEMATICS I am concentrating in this article on two main subjects. Firstly: I am trying to answer the question what brought about such an “explosion” of mathematics in a country in whose scientific tradition there was hardly any mathematics and which happened at the time when after an over-one-century-long foreign rule the nation was trying hard to reconstruct its now independent country, ravaged by the First World War. Secondly: was this explosion a short-lived enthusiasm or, on the contrary, the Polish school of .mathematics struck roots so deeply that it was sub sequently able to survive the cataclysm of the Second World War and rebuild in the new circumastances — in People’s Poland — the internationally re cognized edifice of Polish mathematics? There will be in this article no mathematical theorems, no definitions or geometrical constructions. I shall be trying to use the language which can be understood without mathematical qualifications. It is therefore my hope that this text will be intelligible not only to mathematicians.1 1. PRECURSORS OF THE POLISH SCHOOL OF MATHEMATICS It was the years 1918—1920 when the Polish School of Mathematics was emerging. Before describing this period and the subsequent years one should, I think, review, be it only summarily, the contemporary state of Polish mathematics. I am going to mention those of its representatives the majority of whom had in fact been active in the 19th century but who also worked in the 20th century and so could influence the formation of the School of Mathematics being thus its precursors as it were. -
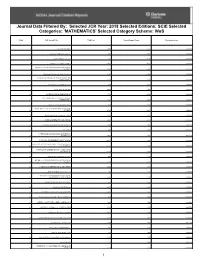
Maths Ranking
Journal Data Filtered By: Selected JCR Year: 2018 Selected Editions: SCIE Selected Categories: 'MATHEMATICS' Selected Category Scheme: WoS Rank Full Journal Title Total Cites Journal Impact Factor Eigenfactor Score 1 ACTA NUMERICA 1,999 7.417 0.003320 2 Advances in Nonlinear Analysis 478 6.636 0.002880 3 Forum of Mathematics Pi 130 5.250 0.002740 4 ANNALS OF MATHEMATICS 12,419 4.165 0.020860 JOURNAL OF THE AMERICAN MATHEMATICAL 5 SOCIETY 3,694 4.091 0.012320 6 Fractional Calculus and Applied Analysis 2,108 3.514 0.004630 COMMUNICATIONS ON PURE AND APPLIED 7 MATHEMATICS 9,332 3.138 0.015600 8 Journal of Numerical Mathematics 469 3.107 0.000890 9 ACTA MATHEMATICA 4,401 3.045 0.004710 10 INVENTIONES MATHEMATICAE 9,739 2.906 0.024290 FOUNDATIONS OF COMPUTATIONAL 11 MATHEMATICS 1,702 2.540 0.006730 12 Advances in Calculus of Variations 211 2.316 0.002000 MEMOIRS OF THE AMERICAN MATHEMATICAL 13 SOCIETY 2,710 2.297 0.006080 14 Publications Mathematiques de l IHES 1,683 2.263 0.004270 15 DUKE MATHEMATICAL JOURNAL 6,593 2.199 0.019120 16 RUSSIAN MATHEMATICAL SURVEYS 3,085 2.038 0.003810 17 CALCOLO 649 1.981 0.001550 JOURNAL DE MATHEMATIQUES PURES ET 18 APPLIQUEES 3,422 1.961 0.011530 19 JOURNAL OF DIFFERENTIAL EQUATIONS 14,837 1.938 0.039920 ANNALES SCIENTIFIQUES DE L ECOLE NORMALE 20 SUPERIEURE 2,715 1.932 0.008410 JOURNAL FUR DIE REINE UND ANGEWANDTE 21 MATHEMATIK 6,139 1.859 0.015290 22 Analysis and Mathematical Physics 226 1.792 0.000850 JOURNAL OF THE EUROPEAN MATHEMATICAL 23 SOCIETY 1,816 1.780 0.016790 24 JOURNAL OF DIFFERENTIAL GEOMETRY -

Document Mune
DOCUMENT MUNE ID 175 699 SE 028 687 AUTHOR Schaaf, William L., Ed. TITLE Reprint Series: Memorable Personalities in Mathematics - Twentieth Century. RS-12. INSTITUTION Stanford Gniv.e Calif. School Mathematics Study Group. 2 SPONS AGENCT National Science Foundation, Washington, D.C. 1 PUB DATE 69 NOTE 54p.: For related documents, see SE 028 676-690 EDRS PRICE 81101/PC03 Plus Postage. DESCRIPTORS Curriculum: *Enrichsent: *History: *Instruction: *Mathematicians: Mathematics Education: *Modern Mathematics: Secondary Education: *Secondary School Sathematics: Supplementary Reading Materials IDENTIFIERS *School Mathematics study Group ABSTRACT This is one in a series of SHSG supplementary and enrichment pamphlets for high school students. This series makes available espcsitory articles which appeared in a variety of mathematical periodials. Topics covered include:(1) Srinivasa Ramanuian:12) Minkomski: (3) Stefan Banach:(4) Alfred North Whitehead: (5) Waclaw Sierptnski: and (6)J. von Neumann. (MP) *********************************************************************** Reproductions supplied by EDRS are the best that can be made from the original document. *********************************************************************** OF NEM TN U S DEPARTMENT "PERMISSION EDUCATION II %WELFARE TO REPROnUCE OF MATERIAL THIS NATIONAL INSTITUTE HAS SEEN EDUCATION GRANTEDBY wc 0Oi ,,V11. NTHt.',Iii t iFf I ROF' all( F 0 f IA. T v A WI (I 1 Ttit P1I4S0 1.41114')WGAN,ZTIf)N01414014 AIHF0,tfvf1,14 Ts 01 ,11-A OF: Ofolv4ION.y STAll 0 04.3 NOT NI-I E55A1,0)V REPRE ,Ak NAFaINA, INSIF011 Of SF Fe 1)1. F P01,I Ot,t AT ION P00,0T,0IN OkI TO THE EDUCATIONAL INFORMATION RESOURCES CENTER(ERIC)." Financial support for the School Mathematics Study Group bas been provided by the National Science Foundation. -

William Chen-Mertens
William Chen-Mertens Contact York University Information Department of Mathematics & Statistics [email protected] Toronto, ON Canada Research Logic and set theory | especially set-theoretic topology and singular cardinal combi- Interests natorics. Employment York University York Science Fellowship (2018{present) Ben-Gurion University of the Negev Postdoctoral Fellowship (2016{2018) Education University of California, Los Angeles Ph.D. in Mathematics (2016) • Dissertation Topic: Some Results on Tight Stationarity • Advisor: Itay Neeman California Institute of Technology B.S. in Mathematics (2010) Publications (with M. Kojman and J. Steprans) Strong colorings over partitions. submitted. (with P.J. Szeptycki) Selectivity properties of spaces. accepted to Topology Proceed- ings. (with P.J. Szeptycki) The effect of forcing axioms on the tightness of the Gδ topology. accepted to Fundamenta Mathematicae. (with G. Galgon) Antichains, the stick principle, and a matching number. Topology and its Applications 256 (2019), 73{85. (with S. Garti and T. Weinert) Cardinal characteristics of the continuum and partitions. to appear in the Israel Journal of Mathematics. Variations of the stick principle. European Journal of Mathematics 3 (2017), 650{658. (with C. Scaduto) Nilpotency in instanton homology, and the framed instanton homol- ogy of a surface times a circle. Advances in Mathematics 336 (2018), 377{408. (with I. Neeman) On the relationship between mutual and tight stationarity. submitted. Tight stationarity and tree-like scales. Annals of Pure and Applied Logic 166 (2015), Issue 10, 1019{1036. (with I. Neeman) Square principles with tail-end agreement. Archive for Mathematical Logic 54 (2015), Issue 3-4, 439{452. Curriculum Vitae, William Chen, 1 (with C.-Y. -

SCIENCE CITATION INDEX EXPANDED - MATHEMATICS - JOURNAL LIST Total Journals: 285
SCIENCE CITATION INDEX EXPANDED - MATHEMATICS - JOURNAL LIST Total journals: 285 1. ABHANDLUNGEN AUS DEM MATHEMATISCHEN SEMINAR DER UNIVERSITAT HAMBURG Annual ISSN: 0025-5858 SPRINGER HEIDELBERG, TIERGARTENSTRASSE 17, HEIDELBERG, GERMANY, D- 69121 1. Science Citation Index Expanded 2. ABSTRACT AND APPLIED ANALYSIS Monthly ISSN: 1085-3375 HINDAWI PUBLISHING CORPORATION, 410 PARK AVENUE, 15TH FLOOR, #287 PMB, NEW YORK, USA, NY, 10022 1. Science Citation Index Expanded 2. Current Contents - Physical, Chemical & Earth Sciences 3. ACTA ARITHMETICA Semimonthly ISSN: 0065-1036 POLISH ACAD SCIENCES INST MATHEMATICS, SNIADECKICH 8, PO BOX 21,, WARSAW 10, POLAND, 00-956 1. Science Citation Index 2. Science Citation Index Expanded 3. Current Contents - Physical, Chemical & Earth Sciences 4. ACTA MATHEMATICA Quarterly ISSN: 0001-5962 SPRINGER, VAN GODEWIJCKSTRAAT 30, DORDRECHT, NETHERLANDS, 3311 GZ 1. Science Citation Index 2. Science Citation Index Expanded 3. Current Contents - Physical, Chemical & Earth Sciences 5. ACTA MATHEMATICA HUNGARICA Monthly ISSN: 0236-5294 SPRINGER, VAN GODEWIJCKSTRAAT 30, DORDRECHT, NETHERLANDS, 3311 GZ 1. Science Citation Index Expanded 6. ACTA MATHEMATICA SCIENTIA Quarterly ISSN: 0252-9602 ELSEVIER SCIENCE INC, 360 PARK AVE SOUTH, NEW YORK, USA, NY, 10010-1710 1. Science Citation Index Expanded 7. ACTA MATHEMATICA SINICA-ENGLISH SERIES Bimonthly ISSN: 1439-8516 SPRINGER HEIDELBERG, TIERGARTENSTRASSE 17, HEIDELBERG, GERMANY, D- 69121 1. Science Citation Index Expanded 2. Current Contents - Physical, Chemical & Earth Sciences 8. ADVANCED NONLINEAR STUDIES Quarterly ISSN: 1536-1365 ADVANCED NONLINEAR STUDIES, INC, PO BOX 691204, SAN ANTONIO, USA, TX, 78269 1. Science Citation Index Expanded 2. Current Contents - Physical, Chemical & Earth Sciences 9. ADVANCES IN CALCULUS OF VARIATIONS Quarterly ISSN: 1864-8258 WALTER DE GRUYTER & CO, GENTHINER STRASSE 13, BERLIN, GERMANY, D- 10785 1.