DOCSLIB.ORG

Brahmaputra River by Numerical Modeling

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Brahmaputra River by Numerical Modeling INVESTIGATION OF ARTIFICIAL CHANNELIZATION ON BRAHMAPUTRA RIVER BY NUMERICAL MODELING A DISSERTATION Submitted in partial fulfillment of the requirements for the award of the degree of MASTER OF TECHNOLOGY in WATER RESOURCES DEVELOPMENT (CIVIL) AFEWORK ASHAGRI s1RAL LIA R (2-)88t 14P C ACC• N3 . ........... T• ROOR~~~ Jam'` L S~Jv X 4 X > DEPARTMENT OF WATER RESOURCES DEVELOPMENT AND MANAGEMENT INDIAN INSTITUTE OF TECHNOLOGY ROORKEE ROORKEE -247 667 (INDIA) JUNE, 2012 INDIAN INSTITUTE OF TECHNOLOGY ROORKEE CANDIDA IF 'S DECL21 k lTION I hereby certify that the work which is being presented in the thesis entitled "INVESTIGATION OF ARTIFICIAL, CHANNELIZATION ON BRAHMAPUTRA RIVER BY NUMERICAL MODELING" in partial fulfillment of the requirements for the award of the Degree of MASTER OF TECHNOLOGY in Water Resources Development (Civil Engineering) and submitted in the Department of Water Resources Development and Management of the Indian Institute of Technology Roorkee, is an authentic record of my own work carried out during a period from July, 2010 to June, 2012 under the supervision of Dr. Nayan Sharma, Professor, Department of Water Resources Development and Management, Indian Institute of Technology Roorkee, India. The matter presented in this thesis has not been submitted by me for the award of any other degree of this or any other Institute. Place: Roorkee Date: 41 ,L ~oI L- (AFEWORIC ASHAGRIE) CERTIFICATE This is to certify that the above statement made by the candidate is correct to the best of my knowledge. (Dr. Nayan Sharma) Professor, Department of Water Resources Development and Management IIT Roorkee Roorkee-247667 India ABSTRACT Brahmaputra river system is very complex because of its braided flow pattern and high sediment load. It is one of the most braided river in the world in which the width of the river extends up to 22 km. Constructing hydraulic structures like a bridge across the river along wide cross section will be difficult unless channelization works are provided. The first part of the study is developing a mathematical model for the river by using HEC RAS 4.1.0. Sediment transport capacity of the river has been done by using different method of transportation functions like Ackers-White, Yang and Engelend-Hansen methods. The result shows that Yang's method of transportation function gives a better result for Brahmaputra River when it is compared with the other transportation functions. From these transportation functions Ackers-White method of transportation function gives high value of sediment transport capacity and high value of change in channel invert. The second part of the study is to channelize the river by putting river training structures at selected nodal points. These nodal points are selected . based on the channel geometry and property in which channelization of the river can be possible. Some cross sections of the river are much braided in nature and it may not be economical to confine the flow over the whole reach of the river Flow guide bunds are adopted as a river training structure to confine and guide the flow to a gentle channel. Especially these structures are constructed on the banks of the river at bridge site locations to guide and confine the flow. Other structures which are adopted as channelization work are closing of secondary channels by putting bed bars, permeable• spurs, porcupine screens, Jack Jetty etc. The change of flow parameters have been compared before and after channelization of the river. There is an increase of velocity, shear stress, and sediment capacity at the cross section in which channelization is made' and up to a certain distance downstream of it. The water surface elevation also increases in the upstream sections up to a certain distance depending on the magnitude of the waterway and depth of channel. Key Words: Numerical Model, Sediment Transport, Channelization, Hump/Bed Sill ACKNOWLEDGMENTS Above all I want to thank the Almighty GOD for his eternal Love and helping me in my stay in India and through my life. I would like to express my gratitude to my guide Dr. Nayan Sharma for his invaluable guidance, encouragement, and advice. I highly appreciate his constructive and valuable advices during my study especially on my research work. Without his support this work would not be realized. My gratitude goes to all professors in the department of Water Resources Development and Management for their help during my study in IIT Roorkee. I would like to thank ITEC for granting me to pursue my study and Indian Institute of Technology, Roorkee for giving me the chance to study in India. At last but not least, I would like to express my deepest thanks for my family supporting me through my life. TABLE OF CONTENTS ABSTRACT............................................................................................................................................. i ACKNOWLEDGMENTS.......................................................................................................................ii TABLE OF CONTENTS ................. iii LISTOF FIGURES ................................................................................................................................vi LISTOF TABLES ................................................................................................................................. ix 1. INTRODUCTION ..........................................................................................................................1 1.1. General ....................................................................................................................................1 1.2. Objectives ................................................................................................................................ 3 1.3. Methodology ............................................................................................................................ 3 1.4. Relevance of Study ...................................................................................................................4 2. LITERATURE REVIEW ......................................................................................................... 2.1 Introduction ............................................................................................................................. 5 2.2 Sediment Transport in Alluvial Rivers ...................................................................................... 5 2.2.1 Stream Slope .................................................................................................................... 6 2.2.2 Stream Bed changes during the floods ..............................................................................7 2.2.3 Degradation and Aggradations ..........................................................................................7 2.2 Numerical Modeling of rivers ................................................................................................... 8 2.2.1 Introduction ...................................................................................................................... 8 2.2.2 One-Dimensional and Multi-Dimensional Numerical Models ...........................................9 2.2.3 Available Numerical Models for River Engineering .......................................................10 2.4 HEC RAS, River Analysis System .........................................................................................12 2.4.1 Steady Flow Water Surface Profiles ................................................................................13 2.4.2 Unsteady Flow Simulation ..............................................................................................14 2.4.3 Sediment Transport/Movable Boundary Computations ...................................................14 2.5 Theoretical Basis for One-Dimensional Flow Calculation .......................................................15 2.5.1 Equations for Basic Profile Calculations .........................................................................15 2.5.2 Cross Section Subdivission for Conveyance Calculation .................................................16 2.5.3 Composite Manning's n for the main channel .................................................................17 2.5.4 Evaluation of Mean Kinetic Energy Head ......................................................................18 2.5.5 Friction Loss Evaluation .................................................................................................19 2.5.6 Contraction and Expansion Loss Evaluation ................................................................... 20 iii 2.5.7 Bed Roughnes Functions ..................................................... ...................................... .....20 2.5.8 Sediment Transport Capacity ............................... .......................................... .................20 2.5.9 Sediment Gradation .......................................... ......................................................... .....20 2.5.10 Sediment Transport Functions .....................................................................................21 2.6 Channelization of River ................................................... ........................................ ............... 25 2.6.1 Some Channelized Rivers ............................................................................................... 25 2.7 Previous Studies on Brahmaputra River .................................................................................
Load more

Recommended publications
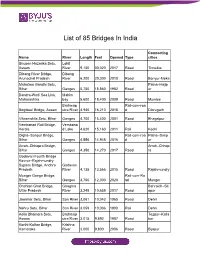
  • List of 85 Bridges in India
    List of 85 Bridges In India Connecting Name River Length Feet Opened Type cities Bhupen Hazarika Setu, Lohit Assam River 9,150 30,020 2017 Road Tinsukia Dibang River Bridge, Dibang Arunachal Pradesh River 6,200 20,300 2018 Road Bomjur-Meka Mahatma Gandhi Setu, Patna–Hajip Bihar Ganges 5,750 18,860 1982 Road ur Bandra-Worli Sea Link, Mahim Maharashtra bay 5,600 18,400 2009 Road Mumbai Brahmap Rail-cum-roa Bogibeel Bridge, Assam utra River 4,940 16,210 2018 d Dibrugarh Vikramshila Setu, Bihar Ganges 4,700 15,400 2001 Road Bhagalpur Vembanad Rail Bridge, Vembana Kerala d Lake 4,620 15,160 2011 Rail Kochi Digha–Sonpur Bridge, Rail-cum-roa Patna–Sonp Bihar Ganges 4,556 14,948 2016 d ur Arrah–Chhapra Bridge, Arrah–Chhap Bihar Ganges 4,350 14,270 2017 Road ra Godavari Fourth Bridge Kovvur–Rajahmundry Bypass Bridge, Andhra Godavari Pradesh River 4,135 13,566 2015 Road Rajahmundry Munger Ganga Bridge, Rail-cum-Ro Bihar Ganges 3,750 12,300 2020 ad Munger Chahlari Ghat Bridge, Ghaghra Bahraich–Sit Uttar Pradesh River 3,249 10,659 2017 Road apur Jawahar Setu, Bihar Son River 3,061 10,043 1965 Road Dehri Nehru Setu, Bihar Son River 3,059 10,036 1900 Rail Dehri Kolia Bhomora Setu, Brahmap Tezpur–Kalia Assam utra River 3,015 9,892 1987 Road bor Korthi-Kolhar Bridge, Krishna Karnataka River 3,000 9,800 2006 Road Bijapur Netaji Subhas Chandra Kathajodi Bose Setu, Odisha River 2,880 9,450 2017 Road Cuttack Godavari Bridge, Andhra Godavari Rail-cum-roa Pradesh River 2,790 1974 d Rajahmundry Old Godavari Bridge Now decommissioned, Godavari Andhra Pradesh
    [Show full text]
  • History of North East India (1228 to 1947)
    HISTORY OF NORTH EAST INDIA (1228 TO 1947) BA [History] First Year RAJIV GANDHI UNIVERSITY Arunachal Pradesh, INDIA - 791 112 BOARD OF STUDIES 1. Dr. A R Parhi, Head Chairman Department of English Rajiv Gandhi University 2. ************* Member 3. **************** Member 4. Dr. Ashan Riddi, Director, IDE Member Secretary Copyright © Reserved, 2016 All rights reserved. No part of this publication which is material protected by this copyright notice may be reproduced or transmitted or utilized or stored in any form or by any means now known or hereinafter invented, electronic, digital or mechanical, including photocopying, scanning, recording or by any information storage or retrieval system, without prior written permission from the Publisher. “Information contained in this book has been published by Vikas Publishing House Pvt. Ltd. and has been obtained by its Authors from sources believed to be reliable and are correct to the best of their knowledge. However, IDE—Rajiv Gandhi University, the publishers and its Authors shall be in no event be liable for any errors, omissions or damages arising out of use of this information and specifically disclaim any implied warranties or merchantability or fitness for any particular use” Vikas® is the registered trademark of Vikas® Publishing House Pvt. Ltd. VIKAS® PUBLISHING HOUSE PVT LTD E-28, Sector-8, Noida - 201301 (UP) Phone: 0120-4078900 Fax: 0120-4078999 Regd. Office: 7361, Ravindra Mansion, Ram Nagar, New Delhi – 110 055 Website: www.vikaspublishing.com Email: [email protected] About the University Rajiv Gandhi University (formerly Arunachal University) is a premier institution for higher education in the state of Arunachal Pradesh and has completed twenty-five years of its existence.
    [Show full text]
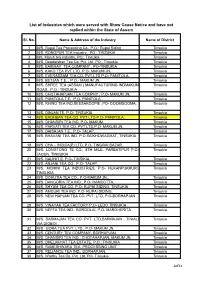
  • List of Industries Which Were Served with Show Cause Notice and Have Not Replied Within the State of Assam
    List of Industries which were served with Show Cause Notice and have not replied within the State of Assam Sl. No. Name & Address of the Industry Name of District 1 M/S. Rupai Tea Processing Co., P.O.: Rupai Siding Tinsukia 2 M/S. RONGPUR TEA Industry., PO.: TINSUKIA Tinsukia 3 M/s. Maruti tea industry, PO.: Tinsukia Tinsukia 4 M/S. Deodarshan Tea Co. Pvt. Ltd ,PO.: Tinsukia Tinsukia 5 M/S. BAIBHAV TEA COMPANY , PO-TINSUKIA Tinsukia 6 M/S. KAKO TEA PVT LTD. P.O- MAKUM JN, Tinsukia 7 M/S. EVERASSAM TEA CO. PVT.LTD P.O- PANITOLA, Tinsukia 8 M/S. BETJAN T.E. , P.O.- MAKUM JN, Tinsukia 9 M/S. SHREE TEA (ASSAM ) MANUFACTURING INDMAKUM Tinsukia ROAD., P.O.: TINSUKIA 10 M/S. CHOTAHAPJAN TEA COMPNY , P.O- MAKUM JN, Tinsukia 11 M/S. PANITOLA T.E. ,P.O- PANITOLA , Tinsukia 12 M/S. RHINO TEA IND.BEESAKOOPIE ,PO- DOOMDOOMA, Tinsukia 13 M/S. DINJAN TE, P.O- TINSUKIA Tinsukia 14 M/S. BAGHBAN TEA CO. PVT LTD P.O- PANITOLA, Tinsukia 15 M/S. DHANSIRI TEA IND. P.O- MAKUM, Tinsukia 16 M/S. PARVATI TEA CO. PVT LTD,P.O- MAKUM JN, Tinsukia 17 M/S. DAISAJAN T.E., P.O- TALAP, Tinsukia 18 M/S. BHAVANI TEA IND. P.O.SAIKHOWAGHAT, TINSUKIA Tinsukia 19 M/S. CHA – INDICA(P) LTD, P.O- TINGRAI BAZAR, Tinsukia 20 M/S. LONGTONG TE CO., 8TH MILE, PARBATIPUR P.O- Tinsukia JAGUN, TINSUKIA 21 M/S. NALINIT.E. P.O- TINSIKIA, Tinsukia 22 M/S.
    [Show full text]
  • Sualkuchi Area of Kamrup District, Assam
    European Scientific Journal December 2014 edition vol.10, No.35 ISSN: 1857 – 7881 (Print) e - ISSN 1857- 7431 THE DYNAMICS IN CHANNEL SHIFT OF THE BRAHMPUTRA ALONG THE AGYATHURI- SUALKUCHI AREA OF KAMRUP DISTRICT, ASSAM Rakesh Chetry, MA Dept. of Geography, Gauhati University, India Abstract Since ages people and rivers have been closely associated with and a slight change in behavior in any aspect has serious repercussions upon the other. Brahmaputra-the lifeline of about 264 lakh population of Assam, has been intrinsically related with the way of life of the inhabitants within its domain and has both positively and negatively affected them. Bank line migration and consequent channel shift is a common phenomena of the mighty river due to its high braided condition and host of other geological as well as other hydrological factors. The study incorporates the Agyathuri- Sualkuchi stretch of Kamrup district, within 5 kms downstream of the Saraighat bridge (the first bridge over Brahmaputra), where the river shows strong northward migrating tendency. Major changes and displacements have been taking place in the region due to channel shift. Keeping in view all these aspects, the paper tries to examine the extent of area encroached by the river since 1911 to 2005 and thereby analyse the causes responsible for channel shift. The specified objectives have been fulfilled based on the utilization of toposheets and google maps in GIS environment including personal field visit. Necessary maps and diagrams have been prepared for exposition of the problem. Keywords: Bank line migration, Braiding, Depopulation, Deposition, Displacement, Erosion Introduction Rivers are dynamic and thus through the process of erosion, transportation and deposition produces dynamic landforms all along its course.
    [Show full text]
  • Lachit Borphukan
    Lachit Borphukan November 25, 2020 In news The Prime Minister has paid tribute to Lachit Borphukan on Lachit Diwas A brief history of Lachit Borphukan He was born on 24th November 1622 at Charaideo in Assam He was the son of Kunti Moran(mother) and Momai Tamuli Borbarua, the1st Borbarua (Phu-Ke-Lung) of upper-Assam and Commander-in-Chief of the Ahom army) under Prataap Singha. Lachit was a commander and Borphukan (Phu-Kon-Lung) in the Ahom kingdom of Assam Other offices held by Lachit before his appointment as Borphukan included Superintendent of the Stable of Royal Horses (Ghora Barua), Commander of the strategic Simulgarh Fort and Superintendent of the Royal Household Guards (Dolakaxaria Barua) for King Chakradhwaj Singha. He is known for his leadership in the 1671 Battle of Saraighat that thwarted a drawn-out attempt by Mughal forces under the command of Ramsingh I to take over Ahom kingdom. King Chakradhwaj Singha selected Lachit to lead the forces of the Kingdom of Ahom to liberate Guwahati from Mughal-occupation. Lachit raised the army and recovered Guwahati from the Mughals and successfully defended it against the Mughal forces during the Battle of Saraighat. He died about a year after the victory at Saraighat due to natural causes. About the Battle of Saraighat It was a naval battle fought in 1671 between the Mughal Empire led by the Kachwaha king, Raja Ramsingh I, and the Ahom Kingdom led by Lachit Borphukan on the Brahmaputra river at Saraighat, now in Guwahati, Assam In this battle the Mughal were defeated by the weaker Ahom Army with its brilliant uses of the terrain, clever diplomatic negotiations to buy time, guerrilla tactics, psychological warfare, military intelligence and by exploiting the sole weakness of the Mughal navy.
    [Show full text]
  • Class-7 New 2020.CDR
    Class - VII Brief Introduction to Formation of Landforms Assam, located in tropical latitudes (24N˚ to 28N)˚ and eastern longitude (895˚ ’ E - 961˚’ E), is the most populous state in the North-east India. It is surrounded on three sides by hills and mountains. The river Brahmaputra and Barak flows in the north and south respectively. Assam is diverse in physical features and the major physiographical components are the senile plateau of Karbi-Anglong, representing a part of peninsular India, North Cachar hills which display the most youthful and highly differentiated relief features and the Brahmaputra and Barak plains present aggradational surfaces. Landmasses from Archaean to Tertiary origin bear the evidences of the evolutionary history of the earth in Assam and North-East India. The Karbi plateau is a part of Old-Gondwana land of more than 600 million years, the folded hills of North-Cachar belongs to tertiary period and the alluviums are of Quaternary Period. The North-Eastern region of India including Assam is situated in the merging zone of two Tectonic plates, namely the Indo-Australian and Euro-Asian plates. So the entire region is seismically very active. Physiographical Divisions of Assam On the basis of physical setup, Assam can be divided into three physiographical units: 1) The Brahmaputra valley or Assam valley 2) The Barak plain or Surma Valley 3) The hilly areas of Karbi-Anglong and North- Cachar Hill Districts Fig1.1: Physiographic Divisions of Assam. 40 The Brahmaputra Valley The most prominent physical feature in Assam is the Brahmaputra valley. This plain is surrounded by Bhutan and the Arunachal Himalayas in the north, Patkai Bum and Arunachal Hills in the east and Naga Hills, Karbi Plateau in the south.
    [Show full text]
  • Post Construction Effect of Bridges on Morphology of River Brahmaputra
    International Journal of Latest Trends in Engineering and Technology Vol.(8)Issue(4), pp.118-125 DOI: http://dx.doi.org/10.21172/1.84.17 e-ISSN:2278-621X POST CONSTRUCTION EFFECT OF BRIDGES ON MORPHOLOGY OF RIVER BRAHMAPUTRA Nayani Deka1 and Dr. Pankaj Goswami2 Abstract- The purpose of bridge construction is to ensure and facilitate the communication over the flow of waterways conveniently.However, these structures have detrimental effects on the hydrology and morphology of the adjacent area of the streams as the waterways is constricted. In this project the effect of construction of bridges on river morphology is the major consideration.In this report Brahmaputra River and its three bridges namely as Saraighat, Koliabhomora, Naranarayan bridge is taken as the study area. Bridge pier construction has already been completed before the present study and some severe morphological response has been observed.This study is carried out to determine the section on d/s of bridges where erosion may be maximum after the construction of bridges and thus bank erosion protective measures to be adopted simultaneously during the time of construction of bridges.A mathematical model is developed to study the relationship between bank erosion, corresponding distance from bridge site, velocity of river at the bridge site and diameter of piles. In this study the simulated result was analyzed with Arc GIS. The result may vary with the river but approach would be the same to resolve this type of difficulties in all rivers and water way. Keywords – Bridge Construction, Morphology, Brahmaputra River, Pier,Bank Erosion, Mathematical Model, Arc GIS I.
    [Show full text]
  • Factors Relating to Decline of Fisheries in the River Aranmaputra
    '".,i.--- " f : Factors relating to decline of fisheries in the river aranmaputra .I I . Bulletin No. 60 ¥ICAR April lW2 Central Inland Capture Fisheries Research Institute (Indian Council of Agricultural Research) B~rrackpore - 743 101 West Bengal India ,I Factors relating to decline of fisheries in the River Brahmaputra Edited & compiled by Y. S. Yadava & V. V. Sugunan tq;.~.1I" Bulletin No. 60 I.C.A.R. April 1992 CENTRAL INLAND CAPTURE FISHERIES RESEARCH INSTITUTE (Indian Council of Agricultural Research) , i -( I Investigation Team Ravish Chandra October 1972-August 22, 1979 M. Chowdhary November 29, 1972 S. N. Upadhyay November 23, 1972-January 4, 1975 v. Kolekar April 18, 1975-June 22, 1981 H. P. Singh March 6, 1972-January 22, 1979 R. K. Singh January 15, 1979-August 9, 1985 Y.S. Yadava January 7, 1980-July 31, 1989 S. P. Singh November 16, 1987-January 31, 1991 S. N. Mehrotra May 7, 1987-September 30, 1991 D. N. Singh August 4, 1972 -August 28, 1987 Released in June 1994 Contents Page No. INTRODUCTION 1 1. THE RIVER 2 1.1 Physiography and fluvial dynamics 2 1.2 Riverine environment and production functions 3 2. FISH AND FISHERIES 5 2.1 Species spectrum 5 2.2 Fish catch composition in major landing centres 5 2.3 Annual trend in fish catch during 1972-80 and 1986-90 6 INVENTORY 8 3.1 Crafts 8 3.2 Gear 8 3.3 The community 11 4. ANTHROPOGENIC IMPACT ON ENVIRONMENT AND FISHERIES 11 4.1 Deforestation and soil erosion in the catchment 11 4.2 Habitat destruction in floodplain lakes 11 4.3 Environmental degradation and its effect on the ri verine fisheries 13 5.
    [Show full text]
  • District at a Glance 1 Chapter
    DISTRICT DISASTER MANAGEMENT PLAN KAMRUP METROPOLITAN DISTRICT DISTRICT DISASTER MANAGEMENT AUTHOURITY, KAMRUP METROPOLITAN DISTRICT DISTRICT AT A GLANCE 1 CHAPTER 1.1. INTRODUCTION: The Present Assam was referred to as Kamrup in many of the ancient Indian literature. It was also known as Pragjyotishpur due to the astrology (Jyotish Shashtra) practices that prevailed in this part of the country during that time. However, "Kamrup" became a more predominant name in the later part of the history. There is a famous story which says the reason behind the naming of this place "Kamrup": Kamrup Metropolitan District is vulnerable to various hazards like flood, landslide, strom, riverbank erosion, urban flash food and water logging. Manmade disasters like fire incident (domestic and commercial), bombblast and road accident also occur time to time. Besides, the entire district falls under seismic zone V. In 1897 and 1950 two major earthquakes divested the region. Recently on 21st September 2009 an earthquake of magnitude 6.2 (epicenter in Bhutan) also affected many buildings in the Guwahati city. This plan focuses on mitigation, preparedness, and operations and defines the Characterization of responder agencies of the district, from within and outside the government. 1.2. DISTRICT PROFILE LOCATION: Kamrup metropolitan district is located between 25o43’and 26o51’ N Latitude and 90o36’ – 92o12’ E Longitude. AREA AND POPULATION: Area : 867.25 Sq. Km Population : 12,60,419 (as per 2011 Census) 1.3. ADMINISTRATIVE UNITS: • This district has one Sub-Divisions-Kamrup Metropolitan Sadar Sub-Division. • The Kamrup Metropolitan district has 6 (Six) Revenue Circles viz. Sonapur RC, Guwahati RC, Azara RC, North Guwahati RC, Chandrapur RC, Dispur RC.
    [Show full text]
  • Lachit Borphukan
    CMYK CMYK The Sentinel P A G E 2 AUGUST 6, 2018 CMYK Lachit Borphukan CMYK Lachit Borphukan, a legend, who was an army general from Assam, is remembered for his extraordinary victory against the Mughal army led by Aurangzeb headed by Ram Singh in the Battle of Saraighat in 1669. Momai Tamuli Borbarua, his father had a humble background but evolved as the first Borbarua (Governor of upper Assam and Commander- in-Chief of the Ahom army) under Turning Prataap Singha. Lachit Borphukan has received differenttraining in humanities, scriptures and military a Penny skills. He was handed over the responsibility of the Soladhara Barua (means scarf-bearer) of the Ahom Swargadeo. It was a position equivalent to a Private Secretaryship, which was regarded as the first step for a Green career as an ambitious diplomat or politician. Prior to being appointed as the Supreme Commander of the army, he held various posts of eminence, such as Superintendent of the Method: Royal Horses or Ghora Barua, Commander of the strategic Soak a paper towel in Simulgarh Fort and Superintendent of the Royal Household vinegar and line the Guards or Dolakasharia Barua assisting the Ahom king. bottom of your tray. The King Chakradhwaj Singha appointed Lachit as the Place the pennies commander in chief of the Ahom army. onto the paper towel. Quite efficiently, Lachit disposed his responsibilities and Sprinkle the pennies transformed it into a strong and powerful army by the with salt. summer of 1667. Literally, he raised the army for the battle soldiers and their Commander-in-chief Lachit Barphukan, Allow the pennies to and preparations were completed by summer of 1667.
    [Show full text]
  • Feasibility Report for Sewerage Schemes
    Pollution Control Board, Assam Conservation of River Bharalu, Guwahati Preparation of Detailed Project Report Project Feasibility Report for Sewerage Schemes December 2013 Joint Venture of The Louis Berger Group, Inc. and DHI (India) Water & Environment Pvt. Ltd. i TABLE OF CONTENTS LIST OF KEY ABBREVIATIONS ..................................................................................... 4 SALIENT FEATURES OF THE PROJECT ...................................................................... 5 EXECUTIVE SUMMARY .................................................................................................. 6 1 ABOUT THE PROJECT AREA .................................................................. 7 1.1 Description of Project Area ..................................................................................... 7 1.1.1 Brief History of the Town ............................................................................................................... 7 1.1.2 Geographical Location .................................................................................................................. 7 1.1.3 Climate .......................................................................................................................................... 9 1.1.4 Topography ................................................................................................................................. 12 1.1.5 Drainage Channels .....................................................................................................................
    [Show full text]
  • ASSAM ACCESSIBLE the Gateway to the North East, Assam Has Seen Rapid Progress in Road Infrastructure Development Since 2014
    MAKING ASSAM ACCESSIBLE The Gateway to the North East, Assam has seen rapid progress in road infrastructure development since 2014. The length of National Highways in the State has reached 3,909 km in 2018. India’s longest bridge, the 9.15 km long Bhupen Hazarika Setu worth Rs. 876 Cr across River Brahmaputra, connecting the Dhola and Sadiya ghats of Assam and Arunachal Pradesh was dedicated to the nation by Prime Minister Narendra Modi in May 2017. Over 300 km of National Highways are being upgraded to 4 lanes, at a cost of over Rs. 10,000 Cr. With engineering marvel projects like Dhubri-Phulbari Bridge & Gohpur-Tumligarh over Brahmaputra being built, the State’s economy is destined to fast track in coming years. “When a network of good roads is created, the economy of the country also picks up pace. Roads are veins and arteries of the nation, which help to transform the pace of development and ensure that prosperity reaches the farthest corners of our nation.” NARENDRA MODI Prime Minister “In the past four years, we have expanded the length of Indian National Highways network to 1,26,350 km. The highway sector in the country has seen a 20% growth between 2014 and 2018. Tourist destinations have come closer. Border, tribal and backward areas are being connected seamlessly. Multimodal integration through road, rail and port connectivity is creating socio economic growth and new opportunities for the people. In the coming years, we have planned projects with investments worth over Rs 6 lakh crore, to further expand the world’s second largest road network.” NITIN GADKARI Union Minister, Ministry of Road Transport & Highways, Shipping and Water Resources, River Development & Ganga Rejuvenation Fast tracking National Highway development in Assam NH + IN PRINCIPLE NH LENGTH UPTO YEAR 2018 3,909 km NH LENGTH UPTO YEAR 2014 3,634 km Adding new National Highways in Assam 1,945 km 798 km Yr 2014 - 2018 Yr 2010 - 2014 New NH New NH & In principle NH length 6 Road Projects awarded in Assam Yr 2010 - 2014 Yr 2014 - 2018 681 km 1,139.77 km Total Cost Total Cost Rs.
    [Show full text]