Complexity of Control of Borda Count Elections
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Critical Strategies Under Approval Voting: Who Gets Ruled in and Ruled Out
Critical Strategies Under Approval Voting: Who Gets Ruled In And Ruled Out Steven J. Brams Department of Politics New York University New York, NY 10003 USA [email protected] M. Remzi Sanver Department of Economics Istanbul Bilgi University 80310, Kustepe, Istanbul TURKEY [email protected] January 2005 2 Abstract We introduce the notion of a “critical strategy profile” under approval voting (AV), which facilitates the identification of all possible outcomes that can occur under AV. Included among AV outcomes are those given by scoring rules, single transferable vote, the majoritarian compromise, Condorcet systems, and others as well. Under each of these systems, a Condorcet winner may be upset through manipulation by individual voters or coalitions of voters, whereas AV ensures the election of a Condorcet winner as a strong Nash equilibrium wherein voters use sincere strategies. To be sure, AV may also elect Condorcet losers and other lesser candidates, sometimes in equilibrium. This multiplicity of (equilibrium) outcomes is the product of a social-choice framework that is more general than the standard preference-based one. From a normative perspective, we argue that voter judgments about candidate acceptability should take precedence over the usual social-choice criteria, such as electing a Condorcet or Borda winner. Keywords: approval voting; elections; Condorcet winner/loser; voting games; Nash equilibrium. Acknowledgments. We thank Eyal Baharad, Dan S. Felsenthal, Peter C. Fishburn, Shmuel Nitzan, Richard F. Potthoff, and Ismail Saglam for valuable suggestions. 3 1. Introduction Our thesis in this paper is that several outcomes of single-winner elections may be socially acceptable, depending on voters’ individual views on the acceptability of the candidates. -

Are Condorcet and Minimax Voting Systems the Best?1
1 Are Condorcet and Minimax Voting Systems the Best?1 Richard B. Darlington Cornell University Abstract For decades, the minimax voting system was well known to experts on voting systems, but was not widely considered to be one of the best systems. But in recent years, two important experts, Nicolaus Tideman and Andrew Myers, have both recognized minimax as one of the best systems. I agree with that. This paper presents my own reasons for preferring minimax. The paper explicitly discusses about 20 systems. Comments invited. [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes Keywords Voting system Condorcet Minimax 1. Many thanks to Nicolaus Tideman, Andrew Myers, Sharon Weinberg, Eduardo Marchena, my wife Betsy Darlington, and my daughter Lois Darlington, all of whom contributed many valuable suggestions. 2 Table of Contents 1. Introduction and summary 3 2. The variety of voting systems 4 3. Some electoral criteria violated by minimax’s competitors 6 Monotonicity 7 Strategic voting 7 Completeness 7 Simplicity 8 Ease of voting 8 Resistance to vote-splitting and spoiling 8 Straddling 8 Condorcet consistency (CC) 8 4. Dismissing eight criteria violated by minimax 9 4.1 The absolute loser, Condorcet loser, and preference inversion criteria 9 4.2 Three anti-manipulation criteria 10 4.3 SCC/IIA 11 4.4 Multiple districts 12 5. Simulation studies on voting systems 13 5.1. Why our computer simulations use spatial models of voter behavior 13 5.2 Four computer simulations 15 5.2.1 Features and purposes of the studies 15 5.2.2 Further description of the studies 16 5.2.3 Results and discussion 18 6. -

MGF 1107 FINAL EXAM REVIEW CHAPTER 9 1. Amy (A), Betsy
MGF 1107 FINAL EXAM REVIEW CHAPTER 9 1. Amy (A), Betsy (B), Carla (C), Doris (D), and Emilia (E) are candidates for an open Student Government seat. There are 110 voters with the preference lists below. 36 24 20 18 8 4 A E D B C C B C E D E D C B C C B B D D B E D E E A A A A A Who wins the election if the method used is: a) plurality? b) plurality with runoff? c) sequential pairwise voting with agenda ABEDC? d) Hare system? e) Borda count? 2. What is the minimum number of votes needed for a majority if the number of votes cast is: a) 120? b) 141? 3. Consider the following preference lists: 1 1 1 A C B B A D D B C C D A If sequential pairwise voting and the agenda BACD is used, then D wins the election. Suppose the middle voter changes his mind and reverses his ranking of A and B. If the other two voters have unchanged preferences, B now wins using the same agenda BACD. This example shows that sequential pairwise voting fails to satisfy what desirable property of a voting system? 4. Consider the following preference lists held by 5 voters: 2 2 1 A B C C C B B A A First, note that if the plurality with runoff method is used, B wins. Next, note that C defeats both A and B in head-to-head matchups. This example shows that the plurality with runoff method fails to satisfy which desirable property of a voting system? 5. -

On the Distortion of Voting with Multiple Representative Candidates∗
The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18) On the Distortion of Voting with Multiple Representative Candidates∗ Yu Cheng Shaddin Dughmi David Kempe Duke University University of Southern California University of Southern California Abstract voters and the chosen candidate in a suitable metric space (Anshelevich 2016; Anshelevich, Bhardwaj, and Postl 2015; We study positional voting rules when candidates and voters Anshelevich and Postl 2016; Goel, Krishnaswamy, and Mu- are embedded in a common metric space, and cardinal pref- erences are naturally given by distances in the metric space. nagala 2017). The underlying assumption is that the closer In a positional voting rule, each candidate receives a score a candidate is to a voter, the more similar their positions on from each ballot based on the ballot’s rank order; the candi- key questions are. Because proximity implies that the voter date with the highest total score wins the election. The cost would benefit from the candidate’s election, voters will rank of a candidate is his sum of distances to all voters, and the candidates by increasing distance, a model known as single- distortion of an election is the ratio between the cost of the peaked preferences (Black 1948; Downs 1957; Black 1958; elected candidate and the cost of the optimum candidate. We Moulin 1980; Merrill and Grofman 1999; Barbera,` Gul, consider the case when candidates are representative of the and Stacchetti 1993; Richards, Richards, and McKay 1998; population, in the sense that they are drawn i.i.d. from the Barbera` 2001). population of the voters, and analyze the expected distortion Even in the absence of strategic voting, voting systems of positional voting rules. -
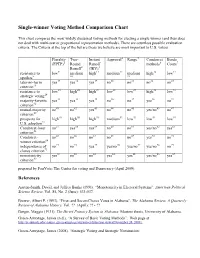
Single-Winner Voting Method Comparison Chart
Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama. -

Voting Procedures and Their Properties
Voting Theory AAAI-2010 Voting Procedures and their Properties Ulle Endriss 8 Voting Theory AAAI-2010 Voting Procedures We’ll discuss procedures for n voters (or individuals, agents, players) to collectively choose from a set of m alternatives (or candidates): • Each voter votes by submitting a ballot, e.g., the name of a single alternative, a ranking of all alternatives, or something else. • The procedure defines what are valid ballots, and how to aggregate the ballot information to obtain a winner. Remark 1: There could be ties. So our voting procedures will actually produce sets of winners. Tie-breaking is a separate issue. Remark 2: Formally, voting rules (or resolute voting procedures) return single winners; voting correspondences return sets of winners. Ulle Endriss 9 Voting Theory AAAI-2010 Plurality Rule Under the plurality rule each voter submits a ballot showing the name of one alternative. The alternative(s) receiving the most votes win(s). Remarks: • Also known as the simple majority rule (6= absolute majority rule). • This is the most widely used voting procedure in practice. • If there are only two alternatives, then it is a very good procedure. Ulle Endriss 10 Voting Theory AAAI-2010 Criticism of the Plurality Rule Problems with the plurality rule (for more than two alternatives): • The information on voter preferences other than who their favourite candidate is gets ignored. • Dispersion of votes across ideologically similar candidates. • Encourages voters not to vote for their true favourite, if that candidate is perceived to have little chance of winning. Ulle Endriss 11 Voting Theory AAAI-2010 Plurality with Run-Off Under the plurality rule with run-off , each voter initially votes for one alternative. -

Computational Perspectives on Democracy
Computational Perspectives on Democracy Anson Kahng CMU-CS-21-126 August 2021 Computer Science Department School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Thesis Committee: Ariel Procaccia (Chair) Chinmay Kulkarni Nihar Shah Vincent Conitzer (Duke University) David Pennock (Rutgers University) Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Copyright c 2021 Anson Kahng This research was sponsored by the National Science Foundation under grant numbers IIS-1350598, CCF- 1525932, and IIS-1714140, the Department of Defense under grant number W911NF1320045, the Office of Naval Research under grant number N000141712428, and the JP Morgan Research grant. The views and conclusions contained in this document are those of the author and should not be interpreted as representing the official policies, either expressed or implied, of any sponsoring institution, the U.S. government or any other entity. Keywords: Computational Social Choice, Theoretical Computer Science, Artificial Intelligence For Grandpa and Harabeoji. iv Abstract Democracy is a natural approach to large-scale decision-making that allows people affected by a potential decision to provide input about the outcome. However, modern implementations of democracy are based on outdated infor- mation technology and must adapt to the changing technological landscape. This thesis explores the relationship between computer science and democracy, which is, crucially, a two-way street—just as principles from computer science can be used to analyze and design democratic paradigms, ideas from democracy can be used to solve hard problems in computer science. Question 1: What can computer science do for democracy? To explore this first question, we examine the theoretical foundations of three democratic paradigms: liquid democracy, participatory budgeting, and multiwinner elections. -

The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity 3
Working Paper The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity Haris Aziz · Barton E. Lee Abstract Proportional representation (PR) is often discussed in voting settings as a major desideratum. For the past century or so, it is common both in practice and in the academic literature to jump to single transferable vote (STV) as the solution for achieving PR. Some of the most prominent electoral reform movements around the globe are pushing for the adoption of STV. It has been termed a major open prob- lem to design a voting rule that satisfies the same PR properties as STV and better monotonicity properties. In this paper, we first present a taxonomy of proportional representation axioms for general weak order preferences, some of which generalise and strengthen previously introduced concepts. We then present a rule called Expand- ing Approvals Rule (EAR) that satisfies properties stronger than the central PR axiom satisfied by STV, can handle indifferences in a convenient and computationally effi- cient manner, and also satisfies better candidate monotonicity properties. In view of this, our proposed rule seems to be a compelling solution for achieving proportional representation in voting settings. Keywords committee selection · multiwinner voting · proportional representation · single transferable vote. JEL Classification: C70 · D61 · D71 1 Introduction Of all modes in which a national representation can possibly be constituted, this one [STV] affords the best security for the intellectual qualifications de- sirable in the representatives—John Stuart Mill (Considerations on Represen- tative Government, 1861). arXiv:1708.07580v2 [cs.GT] 4 Jun 2018 H. Aziz · B. E. Lee Data61, CSIRO and UNSW, Sydney 2052 , Australia Tel.: +61-2-8306 0490 Fax: +61-2-8306 0405 E-mail: [email protected], [email protected] 2 Haris Aziz, Barton E. -

Instructor's Manual
The Mathematics of Voting and Elections: A Hands-On Approach Instructor’s Manual Jonathan K. Hodge Grand Valley State University January 6, 2011 Contents Preface ix 1 What’s So Good about Majority Rule? 1 Chapter Summary . 1 Learning Objectives . 2 Teaching Notes . 2 Reading Quiz Questions . 3 Questions for Class Discussion . 6 Discussion of Selected Questions . 7 Supplementary Questions . 10 2 Perot, Nader, and Other Inconveniences 13 Chapter Summary . 13 Learning Objectives . 14 Teaching Notes . 14 Reading Quiz Questions . 15 Questions for Class Discussion . 17 Discussion of Selected Questions . 18 Supplementary Questions . 21 3 Back into the Ring 23 Chapter Summary . 23 Learning Objectives . 24 Teaching Notes . 24 v vi CONTENTS Reading Quiz Questions . 25 Questions for Class Discussion . 27 Discussion of Selected Questions . 29 Supplementary Questions . 36 Appendix A: Why Sequential Pairwise Voting Is Monotone, and Instant Runoff Is Not . 37 4 Trouble in Democracy 39 Chapter Summary . 39 Typographical Error . 40 Learning Objectives . 40 Teaching Notes . 40 Reading Quiz Questions . 41 Questions for Class Discussion . 42 Discussion of Selected Questions . 43 Supplementary Questions . 49 5 Explaining the Impossible 51 Chapter Summary . 51 Error in Question 5.26 . 52 Learning Objectives . 52 Teaching Notes . 53 Reading Quiz Questions . 54 Questions for Class Discussion . 54 Discussion of Selected Questions . 55 Supplementary Questions . 59 6 One Person, One Vote? 61 Chapter Summary . 61 Learning Objectives . 62 Teaching Notes . 62 Reading Quiz Questions . 63 Questions for Class Discussion . 65 Discussion of Selected Questions . 65 CONTENTS vii Supplementary Questions . 71 7 Calculating Corruption 73 Chapter Summary . 73 Learning Objectives . 73 Teaching Notes . -

Universidade Federal De Pernambuco Centro De Tecnologia E Geociências Departamento De Engenharia De Produção Programa De Pós-Graduação Em Engenharia De Produção
UNIVERSIDADE FEDERAL DE PERNAMBUCO CENTRO DE TECNOLOGIA E GEOCIÊNCIAS DEPARTAMENTO DE ENGENHARIA DE PRODUÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA DE PRODUÇÃO GUILHERME BARROS CORRÊA DE AMORIM RANDOM-SUBSET VOTING Recife 2020 GUILHERME BARROS CORRÊA DE AMORIM RANDOM-SUBSET VOTING Doctoral thesis presented to the Production Engineering Postgraduation Program of the Universidade Federal de Pernambuco in partial fulfillment of the requirements for the degree of Doctor of Science in Production Engineering. Concentration area: Operational Research. Supervisor: Prof. Dr. Ana Paula Cabral Seixas Costa. Co-supervisor: Prof. Dr. Danielle Costa Morais. Recife 2020 Catalogação na fonte Bibliotecária Margareth Malta, CRB-4 / 1198 A524p Amorim, Guilherme Barros Corrêa de. Random-subset voting / Guilherme Barros Corrêa de Amorim. - 2020. 152 folhas, il., gráfs., tabs. Orientadora: Profa. Dra. Ana Paula Cabral Seixas Costa. Coorientadora: Profa. Dra. Danielle Costa Morais. Tese (Doutorado) – Universidade Federal de Pernambuco. CTG. Programa de Pós-Graduação em Engenharia de Produção, 2020. Inclui Referências e Apêndices. 1. Engenharia de Produção. 2. Métodos de votação. 3. Votação probabilística. 4. Racionalidade limitada. 5. Teoria da decisão. I. Costa, Ana Paula Cabral Seixas (Orientadora). II. Morais, Danielle Costa (Coorientadora). III. Título. UFPE 658.5 CDD (22. ed.) BCTG/2020-184 GUILHERME BARROS CORRÊA DE AMORIM RANDOM-SUBSET VOTING Tese apresentada ao Programa de Pós- Graduação em Engenharia de Produção da Universidade Federal de Pernambuco, como requisito parcial para a obtenção do título de Doutor em Engenharia de Produção. Aprovada em: 05 / 05 / 2020. BANCA EXAMINADORA ___________________________________ Profa. Dra. Ana Paula Cabral Seixas Costa (Orientadora) Universidade Federal de Pernambuco ___________________________________ Prof. Leandro Chaves Rêgo, PhD (Examinador interno) Universidade Federal do Ceará ___________________________________ Profa. -

Borda Count, Pairwise Comparison, Approval Voting, Fairness Criteria
Day 2: Borda count, Pairwise Comparison, Approval Voting, Fairness Criteria Recall: Consider the voting system below. Who is the winner under the IRV method? 10 of the voters who had originally voted in the order Brown, Adams, Carter change their vote to favor the presumed winner changing those votes to Adams, Brown, Carter. Who is the winner under the IRV method? Monotonicity Criterion If voters change their votes to increase the preference for a candidate, it should not harm that candidate’s chances of winning. Boda count: (Another voting method, named for Jean-Charles de Borda) In this method, points are assigned to candidates based on their ranking; 1 point for last choice, 2 points for second-to-last choice, and so on. The point values for all ballots are totaled, and the candidate with the largest point total is the winner. Ex1) A camping club is deciding where to go on their next trip. The preference table is shown below, Find the winner under Borda count method. A = Arches, G = Grand Canyon, Y = Yosemite, Z = Zion Number of voters 12 5 4 9 6 10 1st Choice Y G Z A A Z 2nd Choice Z Y A Y Z G 3rd Choice G A G G Y A 4th Choice A Z Y Z G Y Since there are 4 choices 1th Place gets 4 points 2th Place gets 3 points 3th Place gets 2 points 4th Place gets 1point Number of voters 12 5 4 9 6 10 1st Choice Y G Z A A Z 4Point 12.4=48 5.4=20 4.4=16 9.4=36 6.4=24 10.4=40 2nd Choice Z Y A Y Z G 3Point 12.3=36 5.3=15 4.3=12 3rd Choice G A G G Y A 2Point 5.2=1o 10.2=20 4th Choice A Z Y Z G Y 1Point 12.1=12 Total points: Arches = 36 + 24 + 12 +10 +10 +20 +12 = 114 Grand Canyon = 106 Yosemite = 116 Zion = 124 Under the Borda count method Zion is the winner What’s Wrong with Borda Count? One potential flaw of Borda count is a candidate could receive a majority of the first- choice votes and still lose the election. -

A Strength Test for the Borda Count
Bard College Bard Digital Commons Senior Projects Spring 2019 Bard Undergraduate Senior Projects Spring 2019 A Strength Test for the Borda Count Jade Monroe Waring Bard College, [email protected] Follow this and additional works at: https://digitalcommons.bard.edu/senproj_s2019 Part of the Other Mathematics Commons This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. Recommended Citation Waring, Jade Monroe, "A Strength Test for the Borda Count" (2019). Senior Projects Spring 2019. 122. https://digitalcommons.bard.edu/senproj_s2019/122 This Open Access work is protected by copyright and/or related rights. It has been provided to you by Bard College's Stevenson Library with permission from the rights-holder(s). You are free to use this work in any way that is permitted by the copyright and related rights. For other uses you need to obtain permission from the rights- holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/or on the work itself. For more information, please contact [email protected]. A Strength Test for the Borda Count A Senior Project submitted to The Division of Science, Mathematics, and Computing of Bard College by Jade Waring Annandale-on-Hudson, New York May, 2019 ii Abstract When running an election with more than two candidates, there are many ways to choose the winner. A famous theorem of Arrow states that the only mathematically fair way to choose is to do so at random. Because this is not a desirable way to choose a winner of an election, many mathematicians have devised alternate ways of aggregating ballots.