Discovering a Sparse Set of Pairwise Discriminating Features in High Dimensional Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Table S1 the Four Gene Sets Derived from Gene Expression Profiles of Escs and Differentiated Cells
Table S1 The four gene sets derived from gene expression profiles of ESCs and differentiated cells Uniform High Uniform Low ES Up ES Down EntrezID GeneSymbol EntrezID GeneSymbol EntrezID GeneSymbol EntrezID GeneSymbol 269261 Rpl12 11354 Abpa 68239 Krt42 15132 Hbb-bh1 67891 Rpl4 11537 Cfd 26380 Esrrb 15126 Hba-x 55949 Eef1b2 11698 Ambn 73703 Dppa2 15111 Hand2 18148 Npm1 11730 Ang3 67374 Jam2 65255 Asb4 67427 Rps20 11731 Ang2 22702 Zfp42 17292 Mesp1 15481 Hspa8 11807 Apoa2 58865 Tdh 19737 Rgs5 100041686 LOC100041686 11814 Apoc3 26388 Ifi202b 225518 Prdm6 11983 Atpif1 11945 Atp4b 11614 Nr0b1 20378 Frzb 19241 Tmsb4x 12007 Azgp1 76815 Calcoco2 12767 Cxcr4 20116 Rps8 12044 Bcl2a1a 219132 D14Ertd668e 103889 Hoxb2 20103 Rps5 12047 Bcl2a1d 381411 Gm1967 17701 Msx1 14694 Gnb2l1 12049 Bcl2l10 20899 Stra8 23796 Aplnr 19941 Rpl26 12096 Bglap1 78625 1700061G19Rik 12627 Cfc1 12070 Ngfrap1 12097 Bglap2 21816 Tgm1 12622 Cer1 19989 Rpl7 12267 C3ar1 67405 Nts 21385 Tbx2 19896 Rpl10a 12279 C9 435337 EG435337 56720 Tdo2 20044 Rps14 12391 Cav3 545913 Zscan4d 16869 Lhx1 19175 Psmb6 12409 Cbr2 244448 Triml1 22253 Unc5c 22627 Ywhae 12477 Ctla4 69134 2200001I15Rik 14174 Fgf3 19951 Rpl32 12523 Cd84 66065 Hsd17b14 16542 Kdr 66152 1110020P15Rik 12524 Cd86 81879 Tcfcp2l1 15122 Hba-a1 66489 Rpl35 12640 Cga 17907 Mylpf 15414 Hoxb6 15519 Hsp90aa1 12642 Ch25h 26424 Nr5a2 210530 Leprel1 66483 Rpl36al 12655 Chi3l3 83560 Tex14 12338 Capn6 27370 Rps26 12796 Camp 17450 Morc1 20671 Sox17 66576 Uqcrh 12869 Cox8b 79455 Pdcl2 20613 Snai1 22154 Tubb5 12959 Cryba4 231821 Centa1 17897 -

Key Genes Regulating Skeletal Muscle Development and Growth in Farm Animals
animals Review Key Genes Regulating Skeletal Muscle Development and Growth in Farm Animals Mohammadreza Mohammadabadi 1 , Farhad Bordbar 1,* , Just Jensen 2 , Min Du 3 and Wei Guo 4 1 Department of Animal Science, Faculty of Agriculture, Shahid Bahonar University of Kerman, Kerman 77951, Iran; [email protected] 2 Center for Quantitative Genetics and Genomics, Aarhus University, 8210 Aarhus, Denmark; [email protected] 3 Washington Center for Muscle Biology, Department of Animal Sciences, Washington State University, Pullman, WA 99163, USA; [email protected] 4 Muscle Biology and Animal Biologics, Animal and Dairy Science, University of Wisconsin-Madison, Madison, WI 53558, USA; [email protected] * Correspondence: [email protected] Simple Summary: Skeletal muscle mass is an important economic trait, and muscle development and growth is a crucial factor to supply enough meat for human consumption. Thus, understanding (candidate) genes regulating skeletal muscle development is crucial for understanding molecular genetic regulation of muscle growth and can be benefit the meat industry toward the goal of in- creasing meat yields. During the past years, significant progress has been made for understanding these mechanisms, and thus, we decided to write a comprehensive review covering regulators and (candidate) genes crucial for muscle development and growth in farm animals. Detection of these genes and factors increases our understanding of muscle growth and development and is a great help for breeders to satisfy demands for meat production on a global scale. Citation: Mohammadabadi, M.; Abstract: Farm-animal species play crucial roles in satisfying demands for meat on a global scale, Bordbar, F.; Jensen, J.; Du, M.; Guo, W. -

TCF15 Antibody (Center) Affinity Purified Rabbit Polyclonal Antibody (Pab) Catalog # Ap18248c
10320 Camino Santa Fe, Suite G San Diego, CA 92121 Tel: 858.875.1900 Fax: 858.622.0609 TCF15 Antibody (Center) Affinity Purified Rabbit Polyclonal Antibody (Pab) Catalog # AP18248c Specification TCF15 Antibody (Center) - Product Information Application WB,E Primary Accession Q12870 Other Accession Q60756, P79782, NP_004600.2 Reactivity Human Predicted Chicken, Mouse Host Rabbit Clonality Polyclonal Isotype Rabbit Ig Calculated MW 20816 Antigen Region 81-107 TCF15 Antibody (Center) - Additional Information TCF15 Antibody (Center) (Cat. #AP18248c) western blot analysis in K562 cell line lysates Gene ID 6939 (35ug/lane).This demonstrates the TCF15 antibody detected the TCF15 protein (arrow). Other Names Transcription factor 15, TCF-15, Class A basic helix-loop-helix protein 40, bHLHa40, TCF15 Antibody (Center) - Background Paraxis, Protein bHLH-EC2, TCF15, BHLHA40, BHLHEC2 The protein encoded by this gene is found in the nucleus Target/Specificity and may be involved in the early This TCF15 antibody is generated from rabbits immunized with a KLH conjugated transcriptional regulation of synthetic peptide between 81-107 amino patterning of the mesoderm. The encoded acids from the Central region of human basic helix-loop-helix TCF15. protein requires dimerization with another basic helix-loop-helix Dilution protein for efficient DNA binding. WB~~1:1000 TCF15 Antibody (Center) - References Format Purified polyclonal antibody supplied in PBS Guo, P., et al. J. Biol. Chem. with 0.09% (W/V) sodium azide. This 284(27):18184-18193(2009) antibody is purified through a protein A Deloukas, P., et al. Nature column, followed by peptide affinity 414(6866):865-871(2001) purification. Hidai, H., et al. -

Modeling the Human Segmentation Clock with Pluripotent Stem Cells 2 3 Mitsuhiro Matsuda1,10, Yoshihiro Yamanaka2,10, Maya Uemura2,3, Mitsujiro Osawa4, 4 Megumu K
bioRxiv preprint doi: https://doi.org/10.1101/562447; this version posted February 27, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Modeling the Human Segmentation Clock with Pluripotent Stem Cells 2 3 Mitsuhiro Matsuda1,10, Yoshihiro Yamanaka2,10, Maya Uemura2,3, Mitsujiro Osawa4, 4 Megumu K. Saito4, Ayako Nagahashi4, Megumi Nishio3, Long Guo5, Shiro Ikegawa5, 5 Satoko Sakurai6, Shunsuke Kihara7, Michiko Nakamura6, Tomoko Matsumoto6, Hiroyuki 6 Yoshitomi2,3, Makoto Ikeya6, Takuya Yamamoto6,8, Knut Woltjen6,9, Miki Ebisuya1*, 7 Junya Toguchida2,3, Cantas Alev2* 8 9 1 Laboratory for Reconstitutive Developmental Biology, RIKEN Center for Biosystems 10 Dynamics Research (RIKEN BDR), Kobe 650-0047, Japan. 11 2 Department of Cell Growth and Differentiation, Center for iPS Cell Research and 12 Application (CiRA), Kyoto University, Kyoto 606-8507, Japan. 13 3 Department of Regeneration Science and Engineering, Institute for Frontier Life and 14 Medical Sciences, Kyoto University, Kyoto 606-8507, Japan. 15 4 Department of Clinical Application, Center for iPS Cell Research and Application 16 (CiRA), Kyoto University, Kyoto 606-8507, Japan. 17 5 Laboratory for Bone and Joint Diseases, RIKEN Center for Integrative Medical 18 Sciences (RIKEN IMS), Tokyo 108-8639, Japan. 19 6 Department of Life Science Frontiers, Center for iPS Cell Research and Application 20 (CiRA), Kyoto University, 606-8507, Kyoto 108-8639, Japan. 21 7 Department of Fundamental Cell Technology, Center for iPS Cell Research and 22 Application (CiRA), Kyoto University, Kyoto 606-8507, Japan. 23 8 AMED-CREST, AMED 1-7-1 Otemachi, Chiyodaku, Tokyo 100-004, Japan. -

Nanog Regulates Pou3f1 Expression and Represses Anterior Fate at the Exit from Pluripotency
bioRxiv preprint doi: https://doi.org/10.1101/598656; this version posted July 25, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Nanog regulates Pou3f1 expression Barral et al. Nanog regulates Pou3f1 expression and represses anterior fate at the exit from pluripotency Antonio Barral1, *, Isabel Rollan1, *, Hector Sanchez-Iranzo1, 5, Wajid Jawaid2, 3, 6, Claudio Badia-Careaga1, Sergio Menchero1, 7, Manuel J. Gomez1, Carlos Torroja1, Fatima Sanchez-Cabo1, Berthold Göttgens2, 3, Miguel Manzanares1, 4, # and Julio Sainz de Aja1, 8, # 1 Centro Nacional de Investigaciones Cardiovasculares Carlos III (CNIC), Madrid, Spain 2 Wellcome-Medical Research Council Cambridge Stem Cell Institute, Cambridge, UK 3 Department of Haematology, Cambridge Institute for Medical Research, University of Cambridge, Cambridge, UK 4 Centro de Biologia Molecular Severo Ochoa, CSIC-UAM, Madrid, Spain 5 Present address: European Molecular Biology Laboratory (EMBL), Heidelberg, Germany 6 Present address: Addenbrooke's Hospital, Cambridge University Hospitals NHS Foundation Trust, Cambridge Biomedical Campus, Cambridge, UK 7 Present address: The Francis Crick Institute, London, UK 8 Present address: Stem Cell Program, Division of Hematology/Oncology, Children's Hospital Boston, Boston, USA; Department of Genetics, Harvard Medical School, Boston, USA * These authors contributed equally to this work # Corresponding authors: [email protected], [email protected] 1 bioRxiv preprint doi: https://doi.org/10.1101/598656; this version posted July 25, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. -

The DNA Sequence and Comparative Analysis of Human Chromosome 20
articles The DNA sequence and comparative analysis of human chromosome 20 P. Deloukas, L. H. Matthews, J. Ashurst, J. Burton, J. G. R. Gilbert, M. Jones, G. Stavrides, J. P. Almeida, A. K. Babbage, C. L. Bagguley, J. Bailey, K. F. Barlow, K. N. Bates, L. M. Beard, D. M. Beare, O. P. Beasley, C. P. Bird, S. E. Blakey, A. M. Bridgeman, A. J. Brown, D. Buck, W. Burrill, A. P. Butler, C. Carder, N. P. Carter, J. C. Chapman, M. Clamp, G. Clark, L. N. Clark, S. Y. Clark, C. M. Clee, S. Clegg, V. E. Cobley, R. E. Collier, R. Connor, N. R. Corby, A. Coulson, G. J. Coville, R. Deadman, P. Dhami, M. Dunn, A. G. Ellington, J. A. Frankland, A. Fraser, L. French, P. Garner, D. V. Grafham, C. Grif®ths, M. N. D. Grif®ths, R. Gwilliam, R. E. Hall, S. Hammond, J. L. Harley, P. D. Heath, S. Ho, J. L. Holden, P. J. Howden, E. Huckle, A. R. Hunt, S. E. Hunt, K. Jekosch, C. M. Johnson, D. Johnson, M. P. Kay, A. M. Kimberley, A. King, A. Knights, G. K. Laird, S. Lawlor, M. H. Lehvaslaiho, M. Leversha, C. Lloyd, D. M. Lloyd, J. D. Lovell, V. L. Marsh, S. L. Martin, L. J. McConnachie, K. McLay, A. A. McMurray, S. Milne, D. Mistry, M. J. F. Moore, J. C. Mullikin, T. Nickerson, K. Oliver, A. Parker, R. Patel, T. A. V. Pearce, A. I. Peck, B. J. C. T. Phillimore, S. R. Prathalingam, R. W. Plumb, H. Ramsay, C. M. -

Changes in Gene Methylation Patterns in Neonatal Murine Hearts
Górnikiewicz et al. BMC Genomics (2016) 17:231 DOI 10.1186/s12864-016-2545-1 RESEARCH ARTICLE Open Access Changes in gene methylation patterns in neonatal murine hearts: Implications for the regenerative potential Bartosz Górnikiewicz1, Anna Ronowicz2, Michał Krzemiński3 and Paweł Sachadyn1* Abstract Background: The neonatal murine heart is able to regenerate after severe injury; this capacity however, quickly diminishes and it is lost within the first week of life. DNA methylation is an epigenetic mechanism which plays a crucial role in development and gene expression regulation. Under investigation here are the changes in DNA methylation and gene expression patterns which accompany the loss of regenerative potential. Results: The MeDIP-chip (methylated DNA immunoprecipitation microarray) approach was used in order to compare global DNA methylation profiles in whole murine hearts at day 1, 7, 14 and 56 complemented with microarray transcriptome profiling. We found that the methylome transition from day 1 to day 7 is characterized by the excess of genomic regions which gain over those that lose DNA methylation. A number of these changes were retained until adulthood. The promoter genomic regions exhibiting increased DNA methylation at day 7 as compared to day 1 are significantly enriched in the genes critical for heart maturation and muscle development. Also, the promoter genomic regions showing an increase in DNA methylation at day 7 relative to day 1 are significantly enriched with a number of transcription factors binding motifs including those of Mfsd6l, Mef2c, Meis3, Tead4, and Runx1. Conclusions: The results indicate that the extensive alterations in DNA methylation patterns along the development of neonatal murine hearts are likely to contribute to the decline of regenerative capabilities observed shortly after birth. -

GATA2/3-TFAP2A/C Transcription Factor Network Couples Human
GATA2/3-TFAP2A/C transcription factor network couples PNAS PLUS human pluripotent stem cell differentiation to trophectoderm with repression of pluripotency Christian Krendla,1, Dmitry Shaposhnikova,1, Valentyna Rishkoa, Chaido Oria, Christoph Ziegenhainb, Steffen Sassc, Lukas Simonc, Nikola S. Müllerc, Tobias Straubd, Kelsey E. Brookse, Shawn L. Chaveze, Wolfgang Enardb, Fabian J. Theisc,f, and Micha Drukkera,2 aInstitute of Stem Cell Research, Helmholtz Center Munich, 85764 Neuherberg, Germany; bAnthropology and Human Genomics, Department of Biology II, Ludwig-Maximilians University Munich, 82152 Martinsried, Germany; cInstitute of Computational Biology, Helmholtz Center Munich, 85764 Neuherberg, Germany; dBiomedical Center, Core Facility Bioinformatics, Ludwig-Maximilians University Munich, 82152 Martinsried, Germany; eDivision of Reproductive and Developmental Sciences, Oregon National Primate Research Center, Oregon Health and Science University, Beaverton, OR 97006; and fDepartment of Mathematics, Technical University Munich, 85748 Garching, Germany Edited by R. Michael Roberts, University of Missouri, Columbia, MO, and approved September 25, 2017 (received for review May 23, 2017) To elucidate the molecular basis of BMP4-induced differentiation and Elf5, were not unequivocally assigned to the TE lineage in of human pluripotent stem cells (PSCs) toward progeny with human embryos (23). trophectoderm characteristics, we produced transcriptome, epige- Human ESCs (hESCs) and induced pluripotent stem cells nome H3K4me3, H3K27me3, and CpG methylation maps of (iPSCs) can differentiate into trophoblast-like cells by treatment trophoblast progenitors, purified using the surface marker APA. with BMP4, BMP5, BMP10, or BMP13 (24–29). Although these We combined them with the temporally resolved transcriptome of morphogens were not initially implicated in trophoblast develop- the preprogenitor phase and of single APA+ cells. -

The Role of T and Tbx6 During Gastrulation and Determination of Left/Right Asymmetry Daniel Concepcion Submitted in Partial Fulf
The role of T and Tbx6 during gastrulation and determination of left/right asymmetry Daniel Concepcion Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2013 © 2013 Daniel Concepcion All rights reserved Abstract The role of T and Tbx6 in gastrulation and determination of left/right asymmetry Daniel Concepcion T and Tbx6 belong to the T-box family of transcription factors. T homozygous null mutants lack posterior somites after the seventh pair, have no distinguishable notochord, have a convoluted neural tube and die at E.10.5. In this study we investigate the phenotype of a dominant negative allele of T, TWis. Like homozygous embryos carrying the null allele of T, TWis homozygous mutants have left/right asymmetry defects. We demonstrate that left/right specific genes Cer2, Nodal, and Gdf1 are not expressed in TWis mutants and that the Notch signaling pathway, a pathway necessary for expression of left/right specific genes, is severely perturbed. We find, through the use of confocal and scanning electron microscopy, that TWis homozygous mutants have severe node morphological defects. Molecular analysis shows that TWis mutants have altered expression of the genes Shh, Foxa2 and Gsc, that not only mark structures of the midline and node, but whose expression is essential for the formation and patterning of these structures. Tbx6 homozygous null mutants have enlarged tail buds and ectopic neural tubes in place of posterior somites. Tbx6 homozygous null mutants also have irregular development of anterior somites and left/right asymmetry defects that lead to randomization of heart looping. -

(12) Patent Application Publication (10) Pub. No.: US 2009/0269772 A1 Califano Et Al
US 20090269772A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2009/0269772 A1 Califano et al. (43) Pub. Date: Oct. 29, 2009 (54) SYSTEMS AND METHODS FOR Publication Classification IDENTIFYING COMBINATIONS OF (51) Int. Cl. COMPOUNDS OF THERAPEUTIC INTEREST CI2O I/68 (2006.01) CI2O 1/02 (2006.01) (76) Inventors: Andrea Califano, New York, NY G06N 5/02 (2006.01) (US); Riccardo Dalla-Favera, New (52) U.S. Cl. ........... 435/6: 435/29: 706/54; 707/E17.014 York, NY (US); Owen A. (57) ABSTRACT O'Connor, New York, NY (US) Systems, methods, and apparatus for searching for a combi nation of compounds of therapeutic interest are provided. Correspondence Address: Cell-based assays are performed, each cell-based assay JONES DAY exposing a different sample of cells to a different compound 222 EAST 41ST ST in a plurality of compounds. From the cell-based assays, a NEW YORK, NY 10017 (US) Subset of the tested compounds is selected. For each respec tive compound in the Subset, a molecular abundance profile from cells exposed to the respective compound is measured. (21) Appl. No.: 12/432,579 Targets of transcription factors and post-translational modu lators of transcription factor activity are inferred from the (22) Filed: Apr. 29, 2009 molecular abundance profile data using information theoretic measures. This data is used to construct an interaction net Related U.S. Application Data work. Variances in edges in the interaction network are used to determine the drug activity profile of compounds in the (60) Provisional application No. 61/048.875, filed on Apr. -
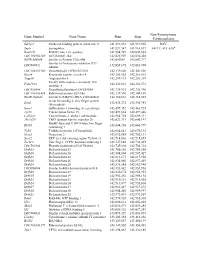
Gene Symbol Gene Name Start Stop Non-Synonymous Polymorphism
Non-Synonymous Gene Symbol Gene Name Start Stop Polymorphism Sdcbp2 Syndecan binding protein (syntenin) 2 141,891,232 141,919,905 I82V Snph Syntaphilin 141,921,547 141,961,697 A411T, 415_420* Rad21l1 RAD21-like 1 (S. pombe) 141,984,729 142,009,665 LOC100363280 mCG140681-like 142,022,959 142,030,458 RGD1564048 Similar to Protein C20orf46 142,043961 142,047,717 Similar to Proteasome inhibitor PI31 LOC689852 142,058,695 142,083,908 subunit LOC100363380 Hypothetical LOC100363380 142,139,020 142,143,826 Rspo4 R-spondin family, member 4 142,185,028 142,216,015 Angpt4 Angiopoietin 4 142,249,115 142,282,307 Family with sequence similarity 110, Fam110a 142,326,013 142,328,572 member A LOC689884 Hypothetical protein LOC689884 142,335,923 142,336,396 LOC100363434 Ribosomal protein S29-like 142,339,596 142,341,169 RGD1304644 Similar to RIKEN cDNA 2310046K01 142,360,661 142,365,285 Scratch homolog 2, zinc finger protein Scrt2 142,434,272 142,445,984 (Drosophila) Srxn1 Sulfiredoxin 1 homolog (S. cerevisiae) 142,457,352 142,462,725 Tcf15 Transcription factor 15 142,491,664 142,497,446 Csnk2a1 Casein kinase 2, alpha 1 polypeptide 142,564,754 142,609,311 Tbc1d20 TBC1 domain family, member 20 142,623,713 142,640,197 RanBP-type and C3HC4-type zinc finger Rbck1 142,644,156 142,660,799 containing 1 Trib3 Tribbles homolog 3 (Drosophila) 142,664,641 142,670,135 Nrsn2 Neurensin 2 142,692,988 142,702,131 Sox12 SRY (sex determining region Y)-box 12 142,714,836 142,715,855 Zcchc3 Zinc finger, CCHC domain containing 3 142,727,648 142,730,465 LOC502684 Hypothetical -

A Meta-Analysis of the Effects of High-LET Ionizing Radiations in Human Gene Expression
Supplementary Materials A Meta-Analysis of the Effects of High-LET Ionizing Radiations in Human Gene Expression Table S1. Statistically significant DEGs (Adj. p-value < 0.01) derived from meta-analysis for samples irradiated with high doses of HZE particles, collected 6-24 h post-IR not common with any other meta- analysis group. This meta-analysis group consists of 3 DEG lists obtained from DGEA, using a total of 11 control and 11 irradiated samples [Data Series: E-MTAB-5761 and E-MTAB-5754]. Ensembl ID Gene Symbol Gene Description Up-Regulated Genes ↑ (2425) ENSG00000000938 FGR FGR proto-oncogene, Src family tyrosine kinase ENSG00000001036 FUCA2 alpha-L-fucosidase 2 ENSG00000001084 GCLC glutamate-cysteine ligase catalytic subunit ENSG00000001631 KRIT1 KRIT1 ankyrin repeat containing ENSG00000002079 MYH16 myosin heavy chain 16 pseudogene ENSG00000002587 HS3ST1 heparan sulfate-glucosamine 3-sulfotransferase 1 ENSG00000003056 M6PR mannose-6-phosphate receptor, cation dependent ENSG00000004059 ARF5 ADP ribosylation factor 5 ENSG00000004777 ARHGAP33 Rho GTPase activating protein 33 ENSG00000004799 PDK4 pyruvate dehydrogenase kinase 4 ENSG00000004848 ARX aristaless related homeobox ENSG00000005022 SLC25A5 solute carrier family 25 member 5 ENSG00000005108 THSD7A thrombospondin type 1 domain containing 7A ENSG00000005194 CIAPIN1 cytokine induced apoptosis inhibitor 1 ENSG00000005381 MPO myeloperoxidase ENSG00000005486 RHBDD2 rhomboid domain containing 2 ENSG00000005884 ITGA3 integrin subunit alpha 3 ENSG00000006016 CRLF1 cytokine receptor like