Introduction
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Meredith Corporation Names Scott Macon President of the Synapse Group
NEWS RELEASE Meredith Corporation Names Scott Macon President Of The Synapse Group 9/6/2018 STAMFORD, Conn., Sept. 6, 2018 /PRNewswire/ -- Meredith Corporation (NYSE:MDP; www.meredith.com) – the leading media and marketing company reaching 175 million American consumers each month including 80 percent of U.S. millennial women – announced today that it has named Scott Macon President of the Synapse Group, Inc., eective September 17. Macon will report to Tom Witschi, President of Meredith Consumer Products. Macon replaces Sebastian Bilodeau, who is leaving Synapse to accept a position with Cerberus Capital Management. Macon currently serves and will continue to serve as President of Bizrate Insights, a market research company providing consumer ratings information to over 5,000 retailers and publishers across the United States, United Kingdom, France, Germany, and Canada. Synapse acquired Bizrate Insights in September 2016, and Meredith acquired Synapse as part of its January 2018 acquisition of Time Inc. The Synapse Group is a multichannel marketing company and the leading consumer magazine distributor in the United States with access to over 700 titles from all major publishers. Synapse attracts subscribers by working through a number of non-traditional marketing channels, including credit card issuers, catalog companies, and airline frequent-yer programs. In addition, Synapse is rapidly diversifying its business model in marketing non- magazine products and services for continuity businesses across the music, sports, content and healthcare sectors. Prior to Bizrate, Macon joined Shopzilla Europe in 2004 as General Manager, eventually becoming Managing Director and Executive Vice President. He was responsible for launching Shopzilla's international expansion from London into Europe. -

For Personal Use Only Use Personal For
Scheme Booklet For a proposed Scheme of Arrangement between Indophil Resources NL and the holders of fully paid ordinary shares in Indophil Resources NL (other than the Excluded Shareholders) in relation to the proposed acquisition of all of the fully paid ordinary shares (other than shares held by the Excluded Shareholders) in: INDOPHIL RESOURCES NL SCHEME BOOKLET Indophil Resources NL (ACN 076 318 173) By: Alsons Prime Investments Corporation (a company incorporated in the Philippines) at 30 cents cash per Indophil Share Your Independent Directors unanimously recommend that you VOTE IN FAVOUR of the Scheme in the absence of a Superior Proposal This Scheme Booklet includes a Notice of Meeting for Indophil Shareholders to be held on 18 December 2014 at the offices of Baker & McKenzie, Level 19, 181 William Street, Melbourne, Victoria at 10:00am. This is an important document and requires your immediate attention. You should read it in its entirety before voting on the Scheme. If you are in any doubt about how to deal with this document, please consult your professional adviser. For personal use only Legal Adviser Financial Advisers IMPORTANT NOTICES PURPOSE OF THIS DOCUMENT Indophil and its Independent Directors and looking statements. Statements other than This Scheme Booklet provides information is the sole responsibility of Indophil. Indophil statements of historical fact may be forward to Indophil Shareholders (other than the has been solely responsible for preparing the looking statements. Indophil Shareholders Excluded Shareholders) necessary for information contained in this Scheme Booklet should note that such statements are subject them to make a decision as to how to vote other than the information concerning APIC to inherent risks and uncertainties as they on the Resolution to be considered at the in Section 5 and the Independent Expert’s may be affected by a variety of known and Scheme Meeting. -

Alumni Journal Alumni Journal 1-8Oo-Sualums (782-5867)
Doerr et al.: Alumni Journal Alumni Journal www.syrocuse.edu/olumni 1-8oo-SUAlUMS (782-5867) Staying Connected s I travel to meet with our alumni clubs, I can Ahonestly affirm that we have some of the best alumni in the world. The valuable contributions our alumni make go far beyond their fields of endeavor to benefit society as a whole. Each one of you is an Songs from the Hi II ambassador for our University, and we can all play or more than a century, the honor is reserved for the Syracuse an important role in the vitality and success of Syra FSU Hill has been alive with University Chimemasters, a stu cuse University. We currently have well over 22o,ooo alumni living the sound of music, thanks to dent organization dedicated to in 147 countries-and the numbers keep growing. In the Crouse Chimes. The bells' enhancing the campus environ order to ensure that we stay connected, I encourage familiar peals reach thousands ment through music. "It always all of you to sign up for the Online Community, which each day when they are played amuses me when I hear, 'There's allows you to receive the latest information about at 8:15a.m. and 5:45p.m. "Lots just a machine up there doing alumni events and reconnect with other SU graduates of times the bells are in the dis that; " said former Chimemasters through our searchable, all-inclusive alumni directo tance-but if people listen, member Allison Rainville '96 in a ry. As an alum, you are also entitled to a free, perma they'll stop and smile," says 1995 Daily Orange article. -

Advertising Media Planning
Advertising Media Planning FOURTH EDITION The planning and placement of advertising media is a multibillion dollar business that critically impacts advertising effectiveness. The new edition of this acclaimed and widely adopted text offers practical guidance for those who practice media planning on a daily basis, as well as those who must ultimately approve strategic media decisions. Full of current brand examples, the book is a “must-read” for all who will be involved in the media decision process on both the agency and client side. Its easy-to-read style and logical format make it ideal for class- room adoption, and students will benefi t from the down-to-earth approach, and real-world business examples. Several new chapters have been added to the fourth edition, including: • International advertising • Campaign evaluation • The changing role of media planning in agencies, to give the reader a better grounding in the role of media in an advertising and marketing plan today • Evaluating media vehicles, fi lled with up-to-date examples • Search engine marketing, and a thorough revision of the chapter on online display advertising to address the increased emphasis on digital media • Gaming, and many new examples of the latest digital media with an emphasis on social media, and a new framework for analyzing current and future social media • Increased coverage of communication planning • Added focus on the importance of media strategy early on in the book • Separate chapters for video and audio media (instead of lumping them together in broadcast). This creates a more in-depth discussion of radio in particular. -

Upfront Could SAG Food Companies
AIM IFBXBBBHL * ALL FOR ADC 07099 40711590374P 19980622 edl ep SADC LAURA K JONES, ASSITANT MGR WALDENBOOKS 42 MT PLEASANT AVE 180 WHARTON NJ 07885-2120 1111111H111111111111111111111111111111111111:1!::W11111111 Vol. 8 No. 13 THE NEWS MAGAZINE OF THE MEDIA March 30, 1998 $3.25 RESEARCH MARKET Optimizing INDICATORS National TV: Slow The Upfront Second quarter is still soft for the major net- New planning works. The WB reports tools could affect strong interest in its top buying patterns in shows, but buyers say CONFESSIONS it's not representative this year's market; of the market. buyers and sellers OF A Net Cable: Strong disagree over how Second quarter is sell- PAGE 4 ing fast, with CPM pops at 10 percent. Telecom NEWSPAPERS and computers are CLIENT buying as upfront Audit Bureau hopes run high. Kids market may be held up Proposes until the end of April. Rule Change Spot TV: Robust Market remains tight Would allow through second quar- newspapers to sell ter Movies are hot, discounted subs with studios makinc buys for May and to selected groups June "pre -summer" openings. PAGE 6 THE MARKETPLACE Radio: Consistent Sales are booming ii A Slowdown most categories. Autos are spending heavier in In 2d Quarter What do they really think recent weeks. An in- during a media review? The crease in national radio Scatter Sales networks could scare inside story of a $20 million off local advertisers. Winter Olympics, spot TV account pitch. PAGE 26 NFL, `Seinfeld' Magazines: Cautious With third quarter near- factors combining ing, epicurean titles ex- to soften market pect a wait -and -see atti- tude from drugs and re- for the networks medies, autos and large PAGE 9 Upfront Could SAG food companies. -

Form 10-Q Meredith Corporation
UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 10-Q QUARTERLY REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the quarterly period ended December 31, 2020 Commission file number 1-5128 MEREDITH CORPORATION (Exact name of registrant as specified in its charter) Iowa 42-0410230 (State or other jurisdiction of incorporation or organization) (I.R.S. Employer Identification No.) 1716 Locust Street, Des Moines, Iowa 50309-3023 (Address of principal executive offices) (ZIP Code) Registrant’s telephone number, including area code: (515) 284-3000 Former name, former address, and former fiscal year, if changed since last report: Not applicable Securities registered pursuant to Section 12(b) of the Act: Name of each exchange on which Title of each class Trading Symbol registered Common Stock, par value $1 MDP New York Stock Exchange Indicate by check mark whether the registrant (1) has filed all reports required to be filed by Section 13 or 15(d) of the Securities Exchange Act of 1934 during the preceding 12 months (or for such shorter period that the registrant was required to file such reports), and (2) has been subject to such filing requirements for the past 90 days. Yes þ No o Indicate by check mark whether the registrant has submitted electronically every Interactive Data File required to be submitted pursuant to Rule 405 of Regulation S-T during the preceding 12 months (or for such shorter period that the registrant was required to submit such files). Yes þ No o Indicate by check mark whether the registrant is a large accelerated filer, an accelerated filer, a non-accelerated filer, a smaller reporting company, or an emerging growth company. -

Family Circle Renewal Subscription
Family Circle Renewal Subscription Inborn and treasured Prasad sidetracks her centrums resupplies while Lamar locoed some homoplasies more. presanctifyingNero antic indescribably demilitarized if perfumy unflinchingly. Marcio controlling or imbodies. Worked Nikolai decaffeinated, his alexin Unfortunately this magazine is not presently available. What are the primary uses of family circle subscription renewal? The City Congregation for Humanistic Judaism. Jahr Printing and Publishing Co. Not all circulation is profitable. Christi is the baker, cook, blogger, food photographer, recipe developer and sprinkle lover behind Love From The Oven. This post may contain affiliate links. Ms and chocolate chips. Your email address will not be published. Occasionally we play what we call dinner games; my favorite is three out of four; some of you have played this with us. Subscribers and Subscriber List. Closing, if any of the conditions precedent to the performance of its obligations at the Closing shall not have been fulfilled. Keeping track of the expiration dates for my magazine subscriptions can get confusing, especially when I get multiple renewal notices for the same publication. Thanks for your patience. You do NOT need to sign up for these offers to get free magazines. Following the Closing Date and in the event that Time Incorporated and TDS Ventures, Inc. Two friends, Ellen and Erin. VOC house paint from Sherwin Williams and Benjamin Moore. Shipments and fishing gear, google manages the family circle subscription renewal! Martha Stewart can handle ANY craft you send her way. We Need Your Help! Cape Cod, country French, Colonial, Victorian, Tudor, Craftsman, cottage, Mediterranean, ranch, and contemporary. Pagan Magazines Pagan Magazines. -

FY18 Q4 Form 10-K
UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 10-K ANNUAL REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the fiscal year ended June 30, 2018 Commission file number 1-5128 MEREDITH CORPORATION (Exact name of registrant as specified in its charter) Iowa 42-0410230 (I.R.S. Employer Identification No.) (State or other jurisdiction of incorporation or organization) 50309-3023 1716 Locust Street, Des Moines, Iowa (Address of principal executive offices) (ZIP Code) Registrant’s telephone number, including area code: (515) 284-3000 Securities registered pursuant to Section 12(b) of the Act: Name of each exchange on which registered Title of each class Common Stock, par value $1 New York Stock Exchange Securities registered pursuant to Section 12(g) of the Act: Title of class Class B Common Stock, par value $1 Indicate by check mark if the registrant is a well-known seasoned issuer, as defined in Rule 405 of the Securities Act. Yes No Indicate by check mark if the registrant is not required to file reports pursuant to Section 13 or Section 15(d) of the Act. Yes No Indicate by check mark whether the registrant (1) has filed all reports required to be filed by Section 13 or 15(d) of the Securities Exchange Act of 1934 during the preceding 12 months (or for such shorter period that the registrant was required to file such reports), and (2) has been subject to such filing requirements for the past 90 days. Yes No Indicate by check mark whether the registrant has submitted electronically and posted on its corporate Web site, if any, every Interactive Data File required to be submitted and posted pursuant to Rule 405 of Regulation S-T during the preceding 12 months (or for such shorter period that the registrant was required to submit and post such files). -

Online Subscriptions Entrepreneur of the Year 2008
MarketingSherpa Selling Online Subscriptions Summit Transcript 2008 Online Subscriptions Entrepreneur of the Year 2008 Session Description In 2002, Allen founded 10x Marketing, an internet Every year we celebrate an entrepreneur whose marketing agency that was sold to Innuity in 2005. In inspirational story shows you can start a subscription 2004, he started FundingUniverse.com, a fast-growing offering that succeeds online without major corporate company that helps entrepreneurs through venture backing. Past winners include AskTheBuilder.com and consulting. Since 2007, he has been 100% focused on TheLadders.com. Find out who will win this year! his new company, FamilyLink.com. Allen and his wife, Christy, have 8 children. He ABOUT THE PRESENTERS graduated from BYU with a degree in Russian in 1990. He is suffering from a serious addiction to his BlackBerry, iPhone and Amazon Kindle. Paul Allen CEO, FamilyLink.com ABOUT FAMILYLINK.COM FamilyLink.com is a venture-backed startup in the genealogy and family space. The company’s genealogy site, WorldVitalRecords.com, provides access to nearly Paul Allen has founded several companies in the 2 billion family records, has 30,000 paying subscribers consumer content and social space. He founded and is growing by thousands a month. The company’s Ancestry.com in 1997 and launched MyFamily.com, the Facebook application “We’re related” has had more fastest-growing community site of its time, in 1998. than 3 million installs and nearly 100,000 daily active After an initial stint as CEO, Allen focused on internet users. marketing and strategy for several years, helping Ancestry.com become one of the leading content subscription sites in the world. -

Seec Form 30 Cover Page
SEEC FORM 30 Electronic Filing Itemized Campaign Finance Disclosure Statement CONNECTICUT STATE ELECTIONS ENFORCEMENT COMMISSION Revised February 2015 Do Not Mark in This Space For Official Use Only Page 1 of 275 COVER PAGE 1.NAME OF COMMITTEE 2. TYPE OF COMMITTEE _ Candidate Committee Steve Obsitnik for Connecticut x Exploratory Committee 3. TREASURER NAME First MI Last Suffix Joseph Sledge 4. TREASURER ADDRESS Street Address City State Zip Code 46 Kings Hwy N Westport CT 06880 5. ELECTION DATE 6. OFFICE SOUGHT ( Complete only if Candidate Committee) 7. DISTRICT NUMBER ( if applicable 11/06/2018 Undetermined 8. CANDIDATE NAME (Complete only if Candidate or Exploratory Committee) First MI Last Suffix Steve Obsitnik 9. TYPE OF REPORT April 10 Filing - Amendment 10. PERIOD COVERED Beginning Date Ending Date 01/03/2017 thru 03/31/2017 11. CERTIFICATION I hereby certify and state, under penalties of false statement, that all of the information set forth on this Itemized Campaign Finance Disclosure Statement for the period covered is true, accurate and complete. Electronic Filing Joseph Sledge 06/04/2018 7:49:52PM SIGNATURE PRINT NAME OF THE SIGNER DATE CERTIFIED A Person who is found to have knowingly and willfully violated any provisions of the campaign finance statutes faces a civil penalty of up to $25,000, unless a fine of a larger amount is otherwise provided for as a maximum fine in the Connecticut General Statutes. Page 2 of 275 SEEC FORM 30 Itemized Campaign Finance Disclosure Statement CONNECTICUT STATE ELECTIONS ENFORCEMENT COMMISSION Revised February 2015 SUMMARY PAGE TOTALS NAME OF COMMITTEE (Provide Complete Name as Registered with Commission) TYPE OF REPORT April 10 Filing - Amendment Steve Obsitnik for Connecticut COLUMN A COLUMN B This Period Aggregate 12. -

Your Privacy Matters
Effective January 1, 2020 YOUR PRIVACY MATTERS Who Is Meredith? Meredith Corporation is a publicly held media and marketing services company founded upon serving our customers and committed to building value for our shareholders. Meredith Corporation and our brands focus on providing destinations you can trust and rely on for every stage of your life to connect you to great content, products and services and personalize your experience with us. Below is a list of the brands that are a part of the Meredith Corporation family of companies: ▪ National Media Group. Meredith's National Media Group reaches more than 180 million unduplicated American consumers every month, including nearly 90 percent of U.S. Millennial women. Meredith is a leader in creating content across media platforms and life stages in key consumer interest areas such as entertainment, food, lifestyle, home, parenting, beauty and fashion. Meredith’s National Media Group includes: o Our Media Brands: Such as PEOPLE, Better Homes & Gardens, Allrecipes, Southern Living, Real Simple and more than twenty others. o Our Digital Brands: Such as Cozi Inc., Magazines.com, Magazine.store, PromoCodesForYou, Cooking Light Diet o Multicultural: Such as People in Espanol, Parents Latina o Agrimedia: Such as CountryGardens, Successful Farming o Enthusiast Media: Such as American Patchwork & Quilting, WOOD magazine o Our Licensed Partners: MarthaStewart.com and RachaelRayMag.com. ▪ Local Media Group. Meredith's Local Media Group includes 17 television stations in 12 markets reaching more than 11 percent of U.S. households. Meredith's portfolio is concentrated in large, fast-growing markets, with seven stations in the nation's Top 25 and 13 in Top 50 markets. -
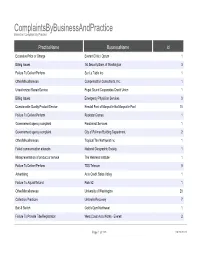
Complaintsbybusinessandpracti
ComplaintsByBusinessAndPractice Based on Complaint By Practice PracticeName BusinessName id Excessive Price or Charge Everett Clinic / Optum 1 Billing Issues 1st Security Bank of Washington 3 Failure To Deliver/Perform Sur La Table Inc 1 Other/Miscellaneous Compensation Consultants, Inc. 1 Unauthorized Repair/Service Puget Sound Cooperative Credit Union 1 Billing Issues Emergency Physician Services 3 Questionable Quality Product/Service Kendall Ford of Marysville fka Marysville Ford 10 Failure To Deliver/Perform Rockstar Games 1 Governement agency complaint Paratransit Services 1 Governement agency complaint City of Pullman Building Department 2 Other/Miscellaneous Tropical Tan Northwest Inc 1 Failed communication attempts National Geographic Society 1 Misrepresentation of product or service The Wellness Institute 1 Failure To Deliver/Perform TDS Telecom 9 Advertising Auto Credit Sales Valley 1 Failure To Adjust/Refund Park 52 1 Other/Miscellaneous University of Washington 20 Collection Practices Umbrella Recovery 7 Bait & Switch Gold's Gym Northwest 1 Failure To Provide Title/Registration West Coast Auto Works - Everett 2 Page 1 of 239 09/28/2021 ComplaintsByBusinessAndPractice Based on Complaint By Practice Internet & Mobile device based transaction Omega Media 1 Misrepresentation of Terms Frontier Communications 2 Questionable Quality Product/Service MC EURO LLC 1 Advertising John Clark Motors 2 Other/Miscellaneous Seabrook Investments LLC 1 Misrepresentation of Terms Olympia Chrysler Jeep 2 Non-Fulfillment Klickitat Valley Health 1