DOCSLIB.ORG

What Is an Interest Rate Swap?

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
What Is an Interest Rate Swap? Project on SWAPS-structure, IRS and how to hedgingSWAPS Submitted to:- Prof. Deepak tendon Submitted by:- Anuradhasharma Group-1 Pg20082421 Swap (finance) In finance, a swap is a derivative in which two counterparties exchange certain benefits of one party's financial instrument for those of the other party's financial instrument. The benefits in question depend on the type of financial instruments involved. Specifically, the two counterparties agree to exchange one stream of cash flows against another stream. These streams are called the legs of the swap. The swap agreement defines the dates when the cash flows are to be paid and the way they are calculated. Usually at the time when the contract is initiated at least one of these series of cash flows is determined by a random or uncertain variable such as an interest rate, foreign exchange rate, equity price or commodity price. The cash flows are calculated over a notional principal amount, which is usually not exchanged between counterparties. Consequently, swaps can be used to create unfunded exposures to an underlying asset, since counterparties can earn the profit or loss from movements in price without having to post the notional amount in cash or collateral. Swaps can be used to hedge certain risks such as interest rate risk, or to speculate on changes in the expected direction of underlying prices. The first swaps were negotiated in the early 1980s. David Swensen, a Yale Ph.D. at Salomon Brothers, engineered the first swap transaction according to "When Genius Failed: The Rise and Fall of Long-Term Capital Management" by Roger Lowenstein. Today, swaps are among the most heavily traded financial contracts in the world. Swap market Most swaps are traded over-the-counter (OTC), "tailor-made" for the counterparties. Some types of swaps are also exchanged on futures markets such as the Chicago Mercantile Exchange Holdings Inc., the largest U.S. futures market, the Chicago Board Options Exchange, IntercontinentalExchange and Frankfurt-based Eurex AG. The Bank for International Settlements (BIS) publishes statistics on the notional amounts outstanding in the OTC derivatives market. At the end of 2006, this was USD 415.2 trillion, more than 8.5 times the 2006 gross world product. However, since the cash flow generated by a swap is equal to an interest rate times that notional amount, the cash flow generated from swaps is a substantial fraction of but much less than the gross world product —which is also a cash-flow measure. The majority of this (USD 292.0 trillion) was due to interest rate swaps. These split by currency as: The CDS and currency swap markets are dwarfed by the interest rate swap market. All three markets peaked in mid 2008. Source: BIS Semiannual OTC derivatives statistics at end-December 2008 Notional outstanding in USD trillion Currency End 2000 End 2001 End 2002 End 2003 End 2004 End 2005 End 2006 Euro 16.6 20.9 31.5 44.7 59.3 81.4 112.1 US dollar 13.0 18.9 23.7 33.4 44.8 74.4 97.6 Japanese yen 11.1 10.1 12.8 17.4 21.5 25.6 38.0 Pound sterling 4.0 5.0 6.2 7.9 11.6 15.1 22.3 Swiss franc 1.1 1.2 1.5 2.0 2.7 3.3 3.5 Total 48.8 58.9 79.2 111.2 147.4 212.0 292.0 Source: "The Global OTC Derivatives Market at end-December 2004", BIS, "OTC Derivatives Market Activity in the Second Half of 2006", BIS. Usually, at least one of the legs has a rate that is variable. It can depend on a reference rate, the total return of a swap, an economic statistic, etc. The most important criterion is that it comes from an independent third party, to avoid any conflict of interest. For instance, LIBOR is published by the British Bankers Association, an independent trade body. Types of swaps The five generic types of swaps, in order of their quantitative importance, are: interest rate swaps, currency swaps, credit swaps, commodity swaps and equity swaps. There are also many other types. Interest rate swaps A is currently paying floating, but wants to pay fixed. B is currently paying fixed but wants to pay floating. By entering into an interest rate swap, the net result is that each party can 'swap' their existing obligation for their desired obligation. Normally the parties do not swap payments directly, but rather, each sets up a separate swap with a financial intermediary such as a bank. In return for matching the two parties together, the bank takes a spread from the swap payments. The most common type of swap is a “plain Vanilla” interest rate swap. It is the exchange of a fixed rate loan to a floating rate loan. The life of the swap can range from 2 years to over 15 years. The reason for this exchange is to take benefit from comparative advantage. Some companies may have comparative advantage in fixed rate markets while other companies have a comparative advantage in floating rate markets. When companies want to borrow they look for cheap borrowing i.e. from the market where they have comparative advantage. However this may lead to a company borrowing fixed when it wants floating or borrowing floating when it wants fixed. This is where a swap comes in. A swap has the effect of transforming a fixed rate loan into a floating rate loan or vice versa. For example, party B makes periodic interest payments to party A based on a variable interest rate of LIBOR +70basis points. Party A in turn makes periodic interest payments based on a fixed rate of 8.65%. The payments are calculated over the notional amount. The first rate is called variable, because it is reset at the beginning of each interest calculation period to the then current reference rate, such as LIBOR. In reality, the actual rate received by A and B is slightly lower due to a bank taking a spread. Currency swaps A currency swap involves exchanging principal and fixed rate interest payments on a loan in one currency for principal and fixed rate interest payments on an equal loan in another currency. Just like interest rate swaps, the currency swaps also are motivated by comparative advantage. Commodity swaps A commodity swap is an agreement whereby a floating (or market or spot) price is exchanged for a fixed price over a specified period. The vast majority of commodity swaps involve oil. Equity Swap An equity swap is a special type of total return swap, where the underlying asset is a stock, a basket of stocks, or a stock index. Compared to actually owning the stock, in this case you do not have to pay anything up front, but you do not have any voting or other rights that stock holders do have. Credit default swaps A credit default swap (CDS) is a swap contract in which the buyer of the CDS makes a series of payments to the seller and, in exchange, receives a payoff if a credit instrument - typically a bond or loan - goes into default (fails to pay). Less commonly, the credit event that triggers the payoff can be a company undergoing restructuring, bankruptcy or even just having its credit rating downgraded. CDS contracts have been compared with insurance, because the buyer pays a premium and, in return, receives a sum of money if one of the events specified in the contract occur Other variations There are myriad different variations on the vanilla swap structure, which are limited only by the imagination of financial engineers and the desire of corporate treasurers and fund managers for exotic structures.A total return swap is a swap in which party A pays the total return of an asset, and party B makes periodic interest payments. The total return is the capital gain or loss, plus any interest or dividend payments. Note that if the total return is negative, then party A receives this amount from party B. The parties have exposure to the return of the underlying stock or index, without having to hold the underlying assets. The profit or loss of party B is the same for him as actually owning the underlying asset. An option on a swap is called a swaption. These provide one party with the right but not the obligation at a future time to enter into a swap. A variance swap is an over-the-counter instrument that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock index. A constant maturity swap, also known as a CMS, is a swap that allows the purchaser to fix the duration of received flows on a swap. An Amortising swap is usually an interest rate swap in which the notional principal for the interest payments declines during the life of the swap, perhaps at a rate tied to the prepayment of a mortgage or to an interest rate benchmark such LIBOR. Valuation The value of a swap is the net present value (NPV) of all estimated future cash flows. A swap is worth zero when it is first initiated, however after this time its value may become positive or negative.[1] There are two ways to value swaps: in terms of bond prices, or as a portfolio of forward contracts.[1] Using bond prices While principal payments are not exchanged in an interest rate swap, assuming that these are received and paid at the end of the swap does not change its value.
Load more

Recommended publications
  • Derivative Markets Swaps.Pdf
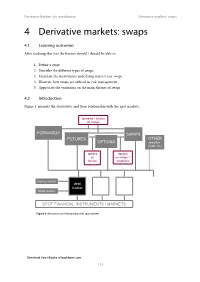
    Derivative Markets: An Introduction Derivative markets: swaps 4 Derivative markets: swaps 4.1 Learning outcomes After studying this text the learner should / should be able to: 1. Define a swap. 2. Describe the different types of swaps. 3. Elucidate the motivations underlying interest rate swaps. 4. Illustrate how swaps are utilised in risk management. 5. Appreciate the variations on the main themes of swaps. 4.2 Introduction Figure 1 presentsFigure the derivatives 1: derivatives and their relationshipand relationship with the spotwith markets. spot markets forwards / futures on swaps FORWARDS SWAPS FUTURES OTHER OPTIONS (weather, credit, etc) options options on on swaps = futures swaptions money market debt equity forex commodity market market market markets bond market SPOT FINANCIAL INSTRUMENTS / MARKETS Figure 1: derivatives and relationship with spot markets Download free eBooks at bookboon.com 116 Derivative Markets: An Introduction Derivative markets: swaps Swaps emerged internationally in the early eighties, and the market has grown significantly. An attempt was made in the early eighties in some smaller to kick-start the interest rate swap market, but few money market benchmarks were available at that stage to underpin this new market. It was only in the middle nineties that the swap market emerged in some of these smaller countries, and this was made possible by the creation and development of acceptable benchmark money market rates. The latter are critical for the development of the derivative markets. We cover swaps before options because of the existence of options on swaps. This illustration shows that we find swaps in all the spot financial markets. A swap may be defined as an agreement between counterparties (usually two but there can be more 360° parties involved in some swaps) to exchange specific periodic cash flows in the future based on specified prices / interest rates.
    [Show full text]
  • Bounding Bermudans
    i i i i Cutting edge: Option pricing Bounding Bermudans Thomas Roos derives model-independent bounds for amortising and accreting Bermudan swaptions in terms of portfolios of standard Bermudan swaptions. In addition to the well-known upper bounds, the author derives new lower bounds for both amortisers and accreters. Numerical results show the bounds to be quite tight in many situations. Applications include model arbitrage checks, limiting valuation uncertainty, and super-replication of long and short positions in the non-standard Bermudan Bermudan swaption gives the holder the right to enter into a fixed no more liquid than the ABerm itself, so their prices must themselves be versus floating swap at a set of future exercise dates. A standard modelled. See Andersen & Piterbarg (2010) for an overview of ABerm A Bermudan swaption (SBerm), sometimes called a ‘bullet’Bermu- calibration methodologies. dan, is characterised by the fact that it is exercisable into a swap whose Whatever methodology is chosen to determine the calibration targets for notional (and fixed rate) is the same for all coupons. In addition to the ABerms, the resulting local calibrationsMedia can be significantly different from important and relatively liquid market for SBerms, there is considerable those used for SBerms. Such differences can translate into inconsistencies interest in accreting and amortising Bermudan swaptions (we will refer and even arbitrage between these closely related products. The bounds to these collectively as ABerms). Accreting Bermudans are exercisable obtained in this article provide a useful safeguard against this kind of into swaps whose notionals increase coupon by coupon, while amortis- model arbitrage.
    [Show full text]
  • Financial Derivatives
    LECTURE NOTES ON FINANCIAL DERIVATIVES MBA IV SEMESTER (IARE – R16) Prepared by Mr. M Ramesh Assistant Professor, Department of MBA DEPARTMENT OF MASTER OF BUSINESS ADMINISTRATION INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad – 500 043 SYLLABUS UNIT- I: INTRODUCTION TO DERIVATIVES Development and growth of derivative markets, types of derivatives uses of derivatives, fundamental linkages between spot & derivative markets, the role of derivatives market, uses and misuses of derivatives. UNIT-II: FUTURE AND FORWARD MARKET Structure of forward and future markets, mechanics of future markets hedging strategies, using futures, determination of forward and future prices, interest rate futures currency futures and forwards. UNIT-III: BASIC OPTION STRATEGIES Options, distinguish between options and futures, structure of options market, principles of option pricing. Option pricing models: the binomial model, the Black-Scholes Merton model. Basic option strategies, advanced option strategies, trading with options, hedging with options, currency options. UNIT-IV: COMMODITY MARKET DERIVATIVES Introduction, types, commodity futures and options, swaps commodity exchanges multi commodity exchange, national commodity derivative exchange role, functions and trading. UNIT-V: SWAPS Concept and nature, evolution of swap market, features of swaps, major types of swaps, interest rate swaps, currency swaps, commodity swaps, equity index swaps, credit risk in swaps, credit swaps, using swaps to manage risk, pricing and valuing swaps. Unit-I INTRODUCTION TO DERIVATIVES \ DERIVATIVE MARKET One of the key features of financial markets are extreme volatility. Prices of foreign currencies, petroleum and other commodities, equity shares and instruments fluctuate all the time, and poses a significant risk to those whose businesses are linked to such fluctuating prices .
    [Show full text]
  • Finance Subcommittee
    MEETING AGENDA FINANCE SUBCOMMITTEE Friday 5 December 2014 at 2pm Council Chamber Chairperson Cr Richard Handley Members: Cr Keith Allum Cr Colin Johnston Cr Craig McFarlane Cr Marie Pearce Mayor Andrew Judd FINANCE SUBCOMMITTEE FRIDAY 5 DECEMBER 2014 Addressing the subcommittee Members of the public have an opportunity to address subcommittees during the public forum section or as a deputation. A public forum section of up to 30 minutes precedes all subcommittee meetings. Each speaker during the public forum section of a meeting may speak for up to 10 minutes. In the case of a group a maximum of 20 minutes will be allowed. A request to make a deputation should be made to the secretariat within two working days before the meeting. The chairperson will decide whether your deputation is accepted. The chairperson may approve a shorter notice period. No more than four members of a deputation may address a meeting. A limit of 10 minutes is placed on a speaker making a presentation. In the case of a group a maximum of 20 minutes will be allowed. Purpose of Local Government The reports contained in this agenda address the requirements of the Local Government Act 2002 in relation to decision making. Unless otherwise stated, the recommended option outlined in each report meets the purpose of local government and: • Will help meet the current and future needs of communities for good-quality local infrastructure, local public services, and performance of regulatory functions in a way that is most cost-effective for households and businesses; • Would not alter significantly the intended level of service provision for any significant activity undertaken by or on behalf of the Council, or transfer the ownership or control of a strategic asset to or from the Council.
    [Show full text]
  • Mastering Financial Calculations
    Mastering Financial Calculations market editions Mastering Financial Calculations A step-by-step guide to the mathematics of financial market instruments ROBERT STEINER London · New York · San Francisco · Toronto · Sydney Tokyo · Singapore · Hong Kong · Cape Town · Madrid Paris · Milan · Munich · Amsterdam PEARSON EDUCATION LIMITED Head Office: Edinburgh Gate Harlow CM20 2JE Tel: +44 (0)1279 623623 Fax: +44 (0)1279 431059 London Office: 128 Long Acre, London WC2E 9AN Tel: +44 (0)20 7447 2000 Fax: +44 (0)20 7240 5771 Website www.financialminds.com First published in Great Britain 1998 Reprinted and updated 1999 © Robert Steiner 1998 The right of Robert Steiner to be identified as author of this work has been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. ISBN 0 273 62587 X British Library Cataloguing in Publication Data A CIP catalogue record for this book can be obtained from the British Library All rights reserved; no part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise without either the prior written permission of the Publishers or a licence permitting restricted copying in the United Kingdom issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1P 0LP. This book may not be lent, resold, hired out or otherwise disposed of by way of trade in any form of binding or cover other than that in which it is published, without the prior consent of the Publishers. 20 19 18 17 16 15 14 13 12 11 Typeset by Pantek Arts, Maidstone, Kent.
    [Show full text]
  • Interest Rate Derivative Conventions
    June 2020 Interest Rate Derivative Conventions Contents Preface: AFMA Code of Conduct .................................................................................................................. 2 1. Description ............................................................................................................................................... 2 2. Products ................................................................................................................................................... 2 2.1. Forward Rate Agreements ....................................................................................................... 2 2.2. Interest Rate Swaps .................................................................................................................. 3 2.3. Basis Swaps ............................................................................................................................... 3 3. Dealing ..................................................................................................................................................... 4 3.1. Methods of Dealing .................................................................................................................. 4 3.2. Electronic Dealing ..................................................................................................................... 4 3.3. Business Days ........................................................................................................................... 4 3.4. Standard Transaction
    [Show full text]
  • Portfolio Management Software]
    [PORTFOLIO MANAGEMENT SOFTWARE] INTRODUCTION Portfolio management is the discipline of planning, organizing, securing and managing resources to bring about the successful completion of specific project goals and objectives. It is sometimes conflated with program management, however technically a program is actually a higher level construct: a group of related and somehow interdependent projects. A project is a temporary endeavor, having a defined beginning and end (usually constrained by date, but can be by funding or deliverables), undertaken to meet unique goals and objectives, usually to bring about beneficial change or added value. The temporary nature of projects stands in contrast to business as usual (or operations), which are repetitive, permanent or semi- permanent functional work to produce products or services. In practice, the management of these two systems is often found to be quite different, and as such requires the development of distinct technical skills and the adoption of separate management. OBJECTIVES OF THE PROJECT • Learning and Understanding the concept of Portfolio. • Understanding the Models of Portfolio Management. • Learning about the Instruments in Portfolio. • Advantages and Diadvantages of Portfolio management • Application of Computer in Portfolio. • Understanding the operation of the Software used in Portfolio. • Advantages of Software used and it limitations. INDIAN INSTITUTE OF FINANCE Page 1 [PORTFOLIO MANAGEMENT SOFTWARE] RESEARCH METHODOLOGY • PRIMARY DATA Primary source is a term used in a number of disciplines to describe source material that is closest to the person, information, period, or idea being studied. • SECONDARY DATA Secondary source is a document or recording that relates or discusses information originally presented elsewhere. A secondary source contrasts with a primary source, which is an original source of the information being discussed.
    [Show full text]
  • Pricing Swaptions on Amortising Swaps
    Pricing Swaptions on Amortising Swaps Ndinae Nico Masutha A dissertation submitted to the Faculty of Commerce, University of Cape Town, in partial fulfillment of the requirementsTown for the degree of Master of Philosophy. Cape Septemberof 17, 2018 MPhil in Mathematical Finance, University of Cape Town. University The copyright of this thesis vests in the author. No quotation from it or information derivedTown from it is to be published without full acknowledgement of the source. The thesis is to be used for private study or non- commercial research purposes Capeonly. of Published by the University of Cape Town (UCT) in terms of the non-exclusive license granted to UCT by the author. University Declaration I declare that this dissertation is my own, unaided work. It is being submitted for the Degree of Master of Philosophy at the University of the Cape Town. It has not been submitted before for any degree or examination in any other University. September 17, 2018 Abstract In this dissertation, two efficient approaches for pricing European options on amor- tising swaps are explored. The first approach is to decompose the pricing of a Euro- pean amortising swaption into a series of discount bond options, with an assump- tion that the interest rate follows a one-factor affine model. The second approach is using a one-dimensional numerical integral technique to approximate the price of European amortising swaption, with an assumption that the interest rate follows an additive two-factor affine model. The efficacy of the two methods was tested by making a comparison with the prices generated using Monte Carlo methods.
    [Show full text]
  • Financial Derivatives
    FINANCIAL DERIVATIVES STUDY MATERIAL VI SEMESTER Core Course : BC6B14 B.COM SPECIALISATION (2017 Admission) UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION Calicut university P.O, Malappuram Kerala, India 673 635. 343 A School of Distance Education UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION STUDY MATERIAL B.Com. Specialization VI Semester BC6B14-FINANCIAL DERIVATIVES Prepared by : Sri. Rajan P Assistant Professor of Commerce School of Distance Education University of Calicut Financial Derivatives Page 2 School of Distance Education Page Modules Contents Number Module 1 Introduction to Financial Derivatives 04-16 Module 2 Derivative Market 17-29 Module 3 Forwards and Futures 30-53 Module 4 Options 54-85 Module 5 Swaps 86-93 Financial Derivatives Page 3 School of Distance Education MODULE 1 INTRODUCTION OF FINANCIAL DERIVATIVES The objective of an investment decision is to get required rate of return with minimum risk. To achieve this objective, various instruments, practices and strategies have been devised and developed in the recent past. With the opening of boundaries for international trade and business, the world trade gained momentum in the last decade, the world has entered into a new phase of global integration and liberalisation. The integration of capital markets world-wide has given rise to increased financial risk with the frequent changes in the interest rates, currency exchange rate and stock prices. To overcome the risk arising out of these fluctuating variables and increased dependence of capital markets of one set of countries to the others, risk management practices have also been reshaped by inventing such instruments as can mitigate the risk element.
    [Show full text]
  • Business Valuation Courses
    The specialist in highly technical, market-driven banking and corporatebanking finance trainingtraining BusinessBanking Valuation Courses Courses All courses can be presented In-House or via Live Webinar web: redliffetraining.co.uk email: [email protected] phone: +44 (0)20 7387 4484 Advanced Negotiation Issues in M&A Brochure Content Date: Location: London Price: .....+VAT BOOK NOW PUBLIC COURSES •Course Advanced Overview Blockchain and Digital Currency Technology • Advanced Debt Restructuring • Anti Money Laundering - Financial Crime Compliance • Asset Based Lending • Bond Documentation • Commercial Real Estate Debt Finance • ISDA DOCUMENTATION • Drafting & Negotiating Issues in Real Estate Finance Documentation • IFRS 9 - The Latest Updates • Negotiating ISDA Master Agreements • Negotiating & Issuing High Yield Bonds • Advanced Negotiation & Structuring Issues in Real Estate Finance Term Sheets • Securitisation - The Structures, Legal Analysis and Documentation • Structured Trade and Commodity Finance • Advanced Trade Finance Training •Course Fundamentals Content of International Trade Finance • Structuring & Negotiating Mezzanine, PIK, Second Lien and Unitranche • The Regulation & Compliance Course for UK Financial Services • Unitranche & Alternative/Direct Lending • Latest Basel IV Regulatory Requirements • Letters of Credit • Trade Based Money Laundering (TBML) & Sanctions Compliance To book this course or find out more, please click the “Book” button Advanced Negotiation Issues in M&A Brochure Content Date: Location:
    [Show full text]
  • Interest Rate Swaps Conventions Contents
    July 2011 Interest Rate Swaps Conventions Contents 1. Description ......................................................................................................................................... 2 2. Products ............................................................................................................................................. 2 3. Dealing ............................................................................................................................................... 2 3.1. Methods of Dealing ............................................................................................................. 2 3.2. Electronic Dealing ................................................................................................................ 2 3.3. Business Days ...................................................................................................................... 3 3.4. Standard Transaction Size (market parcel) ........................................................................... 3 3.5. Two Way Pricing .................................................................................................................. 4 3.6. Quotation and Dealing ......................................................................................................... 4 3.7. Other Instrument Conventions ............................................................................................ 4 3.7.1. CPI Linked Swap Conventions (self contained) ......................................................
    [Show full text]
  • Corporate Treasury Industry Supplement for IFRS 16 'Leases'
    inform.pwc.com In depth A look at current financial reporting issues Corporate treasury industry supplement for IFRS 16 No. 2018-07 ‘Leases’ What’s inside: Background At a glance Practical issues: The new lease accounting standard, IFRS 16, ‘Leases’, will fundamentally change the 1. Discount rates for accounting for lease transactions for lessees and is likely to have significant business lease liabilities ......... 2 implications. It is effective from 1 January 2019. 2. Hedging lessee Almost all leases will be recognised on the balance sheet for a lessee, with a right-of- interest rate risk use asset and a lease liability. Lessees will also generally recognise more expenses in under IFRS 9 ............ 4 profit or loss during the earlier years of a lease. This will have an associated impact on 3. Hedging foreign key accounting metrics, and clear communication will be required to explain the currency risk in leases impact of changes to stakeholders. under IFRS 9 ............ 6 Treasurers at companies adopting IFRS 16 are likely to be involved in its Closing remarks ...... 8 implementation. This publication highlights some common issues and practical solutions relevant to treasurers. These include: determining the appropriate discount rate to use for lease liabilities; potential hedging strategies for interest rate risks inherent in leases; and potential hedging strategies for leases denominated in foreign currencies. Background IFRS 16, the IASB’s leasing standard, is almost upon us. Effective from 1 January 2019, IFRS 16 requires most leases to be treated as financing arrangements, and a resulting right-of-use asset and lease liability to be recorded.
    [Show full text]