DOCSLIB.ORG

Mastering Financial Calculations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mastering Financial Calculations Mastering Financial Calculations market editions Mastering Financial Calculations A step-by-step guide to the mathematics of financial market instruments ROBERT STEINER London · New York · San Francisco · Toronto · Sydney Tokyo · Singapore · Hong Kong · Cape Town · Madrid Paris · Milan · Munich · Amsterdam PEARSON EDUCATION LIMITED Head Office: Edinburgh Gate Harlow CM20 2JE Tel: +44 (0)1279 623623 Fax: +44 (0)1279 431059 London Office: 128 Long Acre, London WC2E 9AN Tel: +44 (0)20 7447 2000 Fax: +44 (0)20 7240 5771 Website www.financialminds.com First published in Great Britain 1998 Reprinted and updated 1999 © Robert Steiner 1998 The right of Robert Steiner to be identified as author of this work has been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. ISBN 0 273 62587 X British Library Cataloguing in Publication Data A CIP catalogue record for this book can be obtained from the British Library All rights reserved; no part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise without either the prior written permission of the Publishers or a licence permitting restricted copying in the United Kingdom issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1P 0LP. This book may not be lent, resold, hired out or otherwise disposed of by way of trade in any form of binding or cover other than that in which it is published, without the prior consent of the Publishers. 20 19 18 17 16 15 14 13 12 11 Typeset by Pantek Arts, Maidstone, Kent. Printed and bound in Great Britain by Redwood Books, Trowbridge, Wiltshire. The Publishers’ policy is to use paper manufactured from sustainable forests. About the Author Robert Steiner is Managing Director of Markets International Ltd, an inde- pendent company specializing in training in a range of areas related to the international financial markets, treasury and banking. The company also provides advice to finance directors and treasurers of international compa- nies on foreign exchange, money markets and other treasury matters. This advice ranges from written studies reviewing existing management policies and procedures, through the development of appropriate hedging strategies, to short-term market advice. Robert was previously senior consultant with HongKong and Shanghai Banking Corporation, where he worked in London and New York in the dealing area as consultant to major US and European companies on treasury management. He has also been treasurer and fund manager of H P Bulmer Holdings PLC and English and American Insurance Group PLC, active in currency and interest rate management. He has thus been closely involved in treasury management as consultant and practitioner. He has also worked in the Overseas Department of the Bank of England, and with the European Commission in Brussels. Robert spends a considerable amount of time training bankers, systems staff, corporate staff and others involved in the financial markets. In particu- lar, he personally runs courses for several of the ACI exams – the ACI Diploma, the Dealing Certificate, Repo Markets and the Settlements Certificate. He is the author of Mastering Repo Markets, also published by Financial Times Prentice Hall. His academic background is an honours degree in mathematics from Cambridge University followed by further studies in economics with London University. He is an associate member of ACI UK, and a member of the Association of Corporate Treasurers. TO MY PARENTS without whom none of this would have been possible AND TO MY FAMILY who have suffered while I’ve been writing it CONTENTS Foreword xi Introduction xiii Part 1: THE BASICS 1Financial Arithmetic Basics 3 Some opening remarks on formulas 4 Use of an HP calculator 4 Simple and compound interest 5 Nominal and effective rates 10 Future value / present value; time value of money 12 Discount factors 15 Cashflow analysis 17 Interpolation and extrapolation 23 Exercises 25 Part 2: INTEREST RATE INSTRUMENTS 2 The Money Market 29 Overview 30 Day/year conventions 32 Money market instruments 34 Money market calculations 38 Discount instruments 40 CDs paying more than one coupon 43 Exercises 47 3Forward-Forwards and Forward Rate Agreements (FRAs) 51 Forward-forwards, FRAs and futures 52 Applications of FRAs 58 Exercises 60 vii Contents 4Interest Rate Futures 63 Overview 64 Exchange structure and margins 66 Futures compared with FRAs 67 Pricing and hedging FRAs with futures 69 Trading with interest rate futures 74 Exercises 79 5 Bond Market Calculations 81 Overview of capital markets instruments 82 Features and variations 84 Introduction to bond pricing 86 Different yield measures and price calculations 95 A summary of the various approaches to price / yield 105 Duration, modified duration and convexity 107 Bond futures 114 Cash-and-carry arbitrage 121 Exercises 130 6 Zero-Coupon Rates and Yield Curves 135 Zero-coupon yields and par yields 136 Forward-forward yields 140 Summary 142 Longer-dated FRAs 143 Exercises 146 Part 3: FOREIGN EXCHANGE 7Foreign Exchange 149 Introduction 149 Spot exchange rates 150 Forward exchange rates 156 Cross-rate forwards 167 Short dates 169 Calculation summary 171 Value dates 172 Forward-forwards 173 Time options 175 Long-dated forwards 176 Synthetic agreements for forward exchange (SAFEs) 176 Arbitraging and creating FRAs 181 Discounting future foreign exchange risk 186 Exercises 189 viii Contents Part 4: SWAPS AND OPTIONS 8Interest Rate and Currency Swaps 195 Basic concepts and applications 196 Pricing 200 Valuing swaps 208 Hedging an interest rate swap 213 Amortising and forward-start swaps 214 Currency swaps 216 Exercises 218 9 Options 221 Overview 222 The ideas behind option pricing 223 Pricing models 228 OTC options vs. exchange-traded options 237 The Greek letters 238 Hedging with options 242 Some “packaged” options 244 Some trading strategies 246 Some less straightforward options 252 Exercises 254 Part 5: FURTHER EXERCISES, HINTS AND ANSWERS 10 Further exercises 257 11 Hints and Answers to Exercises 263 Hints on exercises 264 Answers to exercises 276 Answers to further exercises 316 Appendix 1 Using an HP calculator 329 Appendix 2 A summary of market day/year conventions 337 Appendix 3 A summary of calculation procedures 341 Appendix 4 Glossary 359 Appendix 5 ISO (SWIFT) codes for currencies 381 Select Bibliography 387 Index 389 ix FOREWORD ACI Education (formerly The ACI Institute) is the educational division of ACI – the Financial Markets Association, the primary international profes- sional body for the international financial markets, founded in 1955 and now represented in 59 countries internationally with over 24,000 members. The task of ACI Education is simple to state and is embodied in the Charter of ACI. It is to ensure that educational programmes that reflect the constantly changing nature of the industry are made available to both new entrants to the profession and seasoned professionals, and to set professional standards for the industry globally. This task is both challenging and excit- ing. Recent innovations include the decision to convert the examinations to an electronically delivered format, a change that will facilitate the availability of ACI’s professional testing programme, on a daily basis via a network of over 2,000 test centres globally. One of the component ACI examinations is the Level 2 ACI Diploma that has been running successfully since 1990. Research into ACI’s large database of results yields some interesting findings. Among these it can be seen that one of the best predictors of overall success in the examination has been a good performance on the part of the candidate in the financial calculations section. Conversely, candidates performing badly in this section have often performed poorly, overall, in the examination. ACI, as part of its educational programmes encourages authors, publishers and tutors to provide a wide variety of routes to its examinations as possible. For this reason it is delighted that Robert Steiner and Financial Times Prentice Hall have produced Mastering Financial Calculations. It captures the professional knowledge necessary to appreciate fully the topic, and provides an excellent additional source of study for both the ACI Dealing Certificate and key sections of the ACI Diploma. It also believes that the publication will be appreciated not only by examination candidates but also by the market professionals seeking an ‘easy-to-read’ reference manual on this highly important subject. Heering Ligthart President ACI – The Financial Markets Association xi INTRODUCTION The aim of the book This book is aimed at the very many people in financial institutions, universi- ties and elsewhere who will benefit from a solid grounding in the calculations behind the various financial instruments – dealers, treasurers, investors, pro- grammers, students, auditors and risk managers – but who do not necessarily do complex mathematical puzzles for fun. There is also a strong emphasis on the mechanics, background and applications of all the various instruments. Many dealers would claim to be able to perform their job – essentially buying and selling – very profitably, without using much maths. On the other hand, the different dealing areas in a bank overlap increasingly and it is essential to understand the basis for pricing each instrument, in order to understand how the bank’s position in one relates to a position in another. Almost all the concepts in this book regarding pricing the different instru- ments can be reduced to only two basic ideas. The first concerns the ‘time value of money’: a hundred dollars is worth more if I have it in my hand today than if I do not receive it until next year; or alternatively, for a given amount of cash which I will receive in the future, I can calculate an equiva- lent ‘present value’ now. The second is the ‘no free lunch’ principle: in theory, it should not generally be possible to put together a series of simulta- neous financial transactions which lock in a guaranteed no-risk profit.
Load more

Recommended publications
  • Derivative Markets Swaps.Pdf
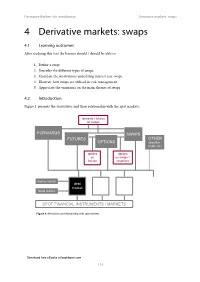
    Derivative Markets: An Introduction Derivative markets: swaps 4 Derivative markets: swaps 4.1 Learning outcomes After studying this text the learner should / should be able to: 1. Define a swap. 2. Describe the different types of swaps. 3. Elucidate the motivations underlying interest rate swaps. 4. Illustrate how swaps are utilised in risk management. 5. Appreciate the variations on the main themes of swaps. 4.2 Introduction Figure 1 presentsFigure the derivatives 1: derivatives and their relationshipand relationship with the spotwith markets. spot markets forwards / futures on swaps FORWARDS SWAPS FUTURES OTHER OPTIONS (weather, credit, etc) options options on on swaps = futures swaptions money market debt equity forex commodity market market market markets bond market SPOT FINANCIAL INSTRUMENTS / MARKETS Figure 1: derivatives and relationship with spot markets Download free eBooks at bookboon.com 116 Derivative Markets: An Introduction Derivative markets: swaps Swaps emerged internationally in the early eighties, and the market has grown significantly. An attempt was made in the early eighties in some smaller to kick-start the interest rate swap market, but few money market benchmarks were available at that stage to underpin this new market. It was only in the middle nineties that the swap market emerged in some of these smaller countries, and this was made possible by the creation and development of acceptable benchmark money market rates. The latter are critical for the development of the derivative markets. We cover swaps before options because of the existence of options on swaps. This illustration shows that we find swaps in all the spot financial markets. A swap may be defined as an agreement between counterparties (usually two but there can be more 360° parties involved in some swaps) to exchange specific periodic cash flows in the future based on specified prices / interest rates.
    [Show full text]
  • The Synthetic Collateralised Debt Obligation: Analysing the Super-Senior Swap Element
    The Synthetic Collateralised Debt Obligation: analysing the Super-Senior Swap element Nicoletta Baldini * July 2003 Basic Facts In a typical cash flow securitization a SPV (Special Purpose Vehicle) transfers interest income and principal repayments from a portfolio of risky assets, the so called asset pool, to a prioritized set of tranches. The level of credit exposure of every single tranche depends upon its level of subordination: so, the junior tranche will be the first to bear the effect of a credit deterioration of the asset pool, and senior tranches the last. The asset pool can be made up by either any type of debt instrument, mainly bonds or bank loans, or Credit Default Swaps (CDS) in which the SPV sells protection1. When the asset pool is made up solely of CDS contracts we talk of ‘synthetic’ Collateralized Debt Obligations (CDOs); in the so called ‘semi-synthetic’ CDOs, instead, the asset pool is made up by both debt instruments and CDS contracts. The tranches backed by the asset pool can be funded or not, depending upon the fact that the final investor purchases a true debt instrument (note) or a mere synthetic credit exposure. Generally, when the asset pool is constituted by debt instruments, the SPV issues notes (usually divided in more tranches) which are sold to the final investor; in synthetic CDOs, instead, tranches are represented by basket CDSs with which the final investor sells protection to the SPV. In any case all the tranches can be interpreted as percentile basket credit derivatives and their degree of subordination determines the percentiles of the asset pool loss distribution concerning them It is not unusual to find both funded and unfunded tranches within the same securitisation: this is the case for synthetic CDOs (but the same could occur with semi-synthetic CDOs) in which notes are issued and the raised cash is invested in risk free bonds that serve as collateral.
    [Show full text]
  • Understanding the Z-Spread Moorad Choudhry*
    Learning Curve September 2005 Understanding the Z-Spread Moorad Choudhry* © YieldCurve.com 2005 A key measure of relative value of a corporate bond is its swap spread. This is the basis point spread over the interest-rate swap curve, and is a measure of the credit risk of the bond. In its simplest form, the swap spread can be measured as the difference between the yield-to-maturity of the bond and the interest rate given by a straight-line interpolation of the swap curve. In practice traders use the asset-swap spread and the Z- spread as the main measures of relative value. The government bond spread is also considered. We consider the two main spread measures in this paper. Asset-swap spread An asset swap is a package that combines an interest-rate swap with a cash bond, the effect of the combined package being to transform the interest-rate basis of the bond. Typically, a fixed-rate bond will be combined with an interest-rate swap in which the bond holder pays fixed coupon and received floating coupon. The floating-coupon will be a spread over Libor (see Choudhry et al 2001). This spread is the asset-swap spread and is a function of the credit risk of the bond over and above interbank credit risk.1 Asset swaps may be transacted at par or at the bond’s market price, usually par. This means that the asset swap value is made up of the difference between the bond’s market price and par, as well as the difference between the bond coupon and the swap fixed rate.
    [Show full text]
  • Macroeconomic and Foreign Exchange Policies of Major Trading Partners of the United States
    REPORT TO CONGRESS Macroeconomic and Foreign Exchange Policies of Major Trading Partners of the United States U.S. DEPARTMENT OF THE TREASURY OFFICE OF INTERNATIONAL AFFAIRS December 2020 Contents EXECUTIVE SUMMARY ......................................................................................................................... 1 SECTION 1: GLOBAL ECONOMIC AND EXTERNAL DEVELOPMENTS ................................... 12 U.S. ECONOMIC TRENDS .................................................................................................................................... 12 ECONOMIC DEVELOPMENTS IN SELECTED MAJOR TRADING PARTNERS ...................................................... 24 ENHANCED ANALYSIS UNDER THE 2015 ACT ................................................................................................ 48 SECTION 2: INTENSIFIED EVALUATION OF MAJOR TRADING PARTNERS ....................... 63 KEY CRITERIA ..................................................................................................................................................... 63 SUMMARY OF FINDINGS ..................................................................................................................................... 67 GLOSSARY OF KEY TERMS IN THE REPORT ............................................................................... 69 This Report reviews developments in international economic and exchange rate policies and is submitted pursuant to the Omnibus Trade and Competitiveness Act of 1988, 22 U.S.C. § 5305, and Section
    [Show full text]
  • Not for Reproduction Not for Reproduction
    Structured Products Europe Awards 2011 to 10% for GuardInvest against 39% for a direct Euro Stoxx 50 investment. “The problem is so many people took volatility as a hedging vehicle over There was also €67.21 million invested in the Theam Harewood Euro time that the price of volatility has gone up, and everybody has suffered Long Dividends Funds by professional investors. Spying the relationship losses of 20%, 30%, 40% on the cost of carry,” says Pacini. “When volatility between dividends and inflation – that finds companies traditionally spiked, people sold quickly, preventing volatility from going up on a paying them in line with inflation – and given that dividends are mark-to-market basis.” House of the year negatively correlated with bonds, the bank’s fund recorded an The bank’s expertise in implied volatility combined with its skills in annualised return of 18.98% by August 31, 2011, against the 1.92% on structured products has allowed it to mix its core long forward variance offer from a more volatile investment in the Euro Stoxx 50. position with a short forward volatility position. The resulting product is BNP Paribas The fund systematically invests in dividend swaps of differing net long volatility and convexity, which protects investors from tail maturities on the European benchmark; the swaps are renewed on their events. The use of variance is a hedge against downside risks and respective maturities. There is an override that reduces exposure to the optimises investment and tail-risk protection. > BNP Paribas was prepared for the worst and liabilities, while providing an attractive yield.
    [Show full text]
  • Central Bank Survey of Foreign Exchange and Derivatives Market Activity
    FR 3036 OMB No. 7100-0285 Hours per Response: 55.0 Approval expires: May 31, 2022 Instructions for the Central Bank Survey of Foreign Exchange and Derivatives Market Activity Turnover Survey April 2019 FR 3036 OMB No. 7100-0285 This report is authorized by law (12 U.S.C. §§ 225a and 263). Your voluntary cooperation in submitting this report is needed to make the results comprehensive, accurate and timely. The Federal Reserve may not conduct or sponsor, and an organization is not required to respond to, a collection of information unless it displays a currently valid OMB control number. The Federal Reserve System regards the individual institution information provided by each respondent as confidential [5 U.S.C. §552(b)(4)]. If it should be determine d that any information collected on this form must be released, other than in the aggregate in ways that will not reveal the amounts reported by any one institution, respondents will be notified. Public reporting burden for this collection of information is estimated to be 55 hours per response, including time to gather and maintain data in the proper form, to review instructions and to complete the information collection. Send comments regarding this burden estimate to: Secretary, Board of Governors of the Federal Reserve System, 20th and C Streets, NW, Washington, DC 20551; and to the Office of Management and Budget, Paperwork Reduction Project, (7100-0285), Washington, DC 20503. Turnover Survey FR 3036 April 2019 Instructions A. Introduction These instructions cover the turnover part of the survey. The turnover part of the survey will be conducted on a locational basis.
    [Show full text]
  • 2016 Triennial Central Bank Survey of Foreign Exchange and OTC Derivatives Market Activity Frequently Asked Questions and Answers
    Restricted 20 January 2016 2016 Triennial Central Bank Survey of Foreign Exchange and OTC Derivatives Market Activity Frequently asked questions and answers Table of Contents A. Risk categories ............................................................................................................... 3 1. Foreign exchange transactions: the reporting of gold ............................................ 3 B. Instruments ..................................................................................................................... 3 1. Reporting of currency options strategies ............................................................... 3 2. Reporting of FX swaps .......................................................................................... 3 3. Categorisation of currency swaptions and interest rate swaptions ........................ 4 4. Reporting of in/out swaps between CLS members ................................................ 4 5. Reporting of “cash/same day” transactions. .......................................................... 4 C. Counterparties ................................................................................................................ 4 1. Definition of reporting dealers ................................................................................ 4 2. The lists of reporting dealers for the two parts of the survey ................................. 5 3. Counterparties in a FX prime brokerage relationship ............................................ 5 4. Treatment of centrally cleared
    [Show full text]
  • Credit Derivatives Handbook
    08 February 2007 Fixed Income Research http://www.credit-suisse.com/researchandanalytics Credit Derivatives Handbook Credit Strategy Contributors Ira Jersey +1 212 325 4674 [email protected] Alex Makedon +1 212 538 8340 [email protected] David Lee +1 212 325 6693 [email protected] This is the second edition of our Credit Derivatives Handbook. With the continuous growth of the derivatives market and new participants entering daily, the Handbook has become one of our most requested publications. Our goal is to make this publication as useful and as user friendly as possible, with information to analyze instruments and unique situations arising from market action. Since we first published the Handbook, new innovations have been developed in the credit derivatives market that have gone hand in hand with its exponential growth. New information included in this edition includes CDS Orphaning, Cash Settlement of Single-Name CDS, Variance Swaps, and more. We have broken the information into several convenient sections entitled "Credit Default Swap Products and Evaluation”, “Credit Default Swaptions and Instruments with Optionality”, “Capital Structure Arbitrage”, and “Structure Products: Baskets and Index Tranches.” We hope this publication is useful for those with various levels of experience ranging from novices to long-time practitioners, and we welcome feedback on any topics of interest. FOR IMPORTANT DISCLOSURE INFORMATION relating to analyst certification, the Firm’s rating system, and potential conflicts
    [Show full text]
  • Asset Swaps and Credit Derivatives
    PRODUCT SUMMARY A SSET S WAPS Creating Synthetic Instruments Prepared by The Financial Markets Unit Supervision and Regulation PRODUCT SUMMARY A SSET S WAPS Creating Synthetic Instruments Joseph Cilia Financial Markets Unit August 1996 PRODUCT SUMMARIES Product summaries are produced by the Financial Markets Unit of the Supervision and Regulation Department of the Federal Reserve Bank of Chicago. Product summaries are pub- lished periodically as events warrant and are intended to further examiner understanding of the functions and risks of various financial markets products relevant to the banking industry. While not fully exhaustive of all the issues involved, the summaries provide examiners background infor- mation in a readily accessible form and serve as a foundation for any further research into a par- ticular product or issue. Any opinions expressed are the authors’ alone and do not necessarily reflect the views of the Federal Reserve Bank of Chicago or the Federal Reserve System. Should the reader have any questions, comments, criticisms, or suggestions for future Product Summary topics, please feel free to call any of the members of the Financial Markets Unit listed below. FINANCIAL MARKETS UNIT Joseph Cilia(312) 322-2368 Adrian D’Silva(312) 322-5904 TABLE OF CONTENTS Asset Swap Fundamentals . .1 Synthetic Instruments . .1 The Role of Arbitrage . .2 Development of the Asset Swap Market . .2 Asset Swaps and Credit Derivatives . .3 Creating an Asset Swap . .3 Asset Swaps Containing Interest Rate Swaps . .4 Asset Swaps Containing Currency Swaps . .5 Adjustment Asset Swaps . .6 Applied Engineering . .6 Structured Notes . .6 Decomposing Structured Notes . .7 Detailing the Asset Swap .
    [Show full text]
  • Fixed Income 2
    2 | Fixed Income Fixed 2 CFA Society Italy CFA Society Italy è l’associazione Italiana dei professionisti che lavorano nell’industria Fixed finanziaria italiana. CFA Society Italy nata nel 1999 come organizzazione no profit, è affiliata a CFA Institute, l’associazione globale di professionisti degli investimenti che definisce gli Income standard di eccellenza per il settore. CFA Society Italy ha attualmente oltre 400 soci attivi, nel mondo i professionisti certificati CFA® sono oltre 150.000. Assegnato per la prima volta nel 1963, CFA® è la designazione di eccellenza professionale per la comunità finanziaria internazionale. Il programma CFA® offre una sfida educativa davvero globale in cui è possibile creare una conoscenza fondamentale dei principi di investimento, rilevante per ogni mercato mondiale. I soci che hanno acquisito la certificazione CFA® incarnano le quattro virtù che sono le caratteristiche distintive di CFA Institute: Etica, Tenacia, Rigore e Analisi. CFA Society Italia offre una gamma di opportunità educative e facilita lo scambio aperto di informazioni e opinioni tra professionisti degli investimenti, grazie ad una serie continua di eventi per i propri membri. I nostri soci hanno la possibilità di entrare in contatto con la comunità finanziaria italiana aumentando il proprio network lavorativo. I membri di CFA Society Italy hanno inoltre la posibilità di partecipare attivamente ad iniziative dell’associazione, che Guida a cura di Con la collaborazione di consentono di fare leva sulle proprie esperienze lavorative. L’iscrizione e il completamento degli esami del programma CFA®, anche se fortemente raccomandati, non sono un requisito per l’adesione e incoraggiamo attivamente i professionisti italiani del settore finanziario a unirsi alla nostra associazione.
    [Show full text]
  • DEPARTMENT of the TREASURY Determination of Foreign Exchange
    This document has been submitted to the Office of the Federal Register (OFR) for publication and is pending placement on public display at the OFR and publication in the Federal Register. The document may vary slightly from the published document if minor editorial changes have been made during the OFR review process. Upon publication in the Federal Register, the regulation can be found at http://www.gpoaccess.gov/fr/, www.regulations.gov, and at www.treasury.gov. The document published in the Federal Register is the official document. DEPARTMENT OF THE TREASURY Determination of Foreign Exchange Swaps and Foreign Exchange Forwards under the Commodity Exchange Act AGENCY: Department of the Treasury, Departmental Offices. ACTION: Notice of Proposed Determination. SUMMARY: The Commodity Exchange Act (―CEA‖), as amended by Title VII of the Dodd-Frank Wall Street Reform and Consumer Protection Act (―Dodd-Frank Act‖), authorizes the Secretary of the Treasury (―Secretary‖) to issue a written determination exempting foreign exchange swaps, foreign exchange forwards, or both, from the definition of a ―swap‖ under the CEA. The Secretary proposes to issue a determination that would exempt both foreign exchange swaps and foreign exchange forwards from the definition of ―swap,‖ in accordance with the relevant provisions of the CEA and invites comment on the proposed determination, as well as the factors supporting such a determination. DATES: Written comments must be received on or before [INSERT DATE THAT IS 30 DAYS AFTER PUBLICATION IN THE FEDERAL REGISTER], to be assured of consideration. ADDRESSES: Submission of Comments by mail: You may submit comments to: Office of Financial Markets, Department of the Treasury, 1500 Pennsylvania Avenue N.W., Washington, DC, 20220.
    [Show full text]
  • Inflation Derivatives: Introduction One of the Latest Developments in Derivatives Markets Are Inflation- Linked Derivatives, Or, Simply, Inflation Derivatives
    Inflation-indexed Derivatives Inflation derivatives: introduction One of the latest developments in derivatives markets are inflation- linked derivatives, or, simply, inflation derivatives. The first examples were introduced into the market in 2001. They arose out of the desire of investors for real, inflation-linked returns and hedging rather than nominal returns. Although index-linked bonds are available for those wishing to have such returns, as we’ve observed in other asset classes, inflation derivatives can be tailor- made to suit specific requirements. Volume growth has been rapid during 2003, as shown in Figure 9.4 for the European market. 4000 3000 2000 1000 0 Jul 01 Jul 02 Jul 03 Jan 02 Jan 03 Sep 01 Sep 02 Mar 02 Mar 03 Nov 01 Nov 02 May 01 May 02 May 03 Figure 9.4 Inflation derivatives volumes, 2001-2003 Source: ICAP The UK market, which features a well-developed index-linked cash market, has seen the largest volume of business in inflation derivatives. They have been used by market-makers to hedge inflation-indexed bonds, as well as by corporates who wish to match future liabilities. For instance, the retail company Boots plc added to its portfolio of inflation-linked bonds when it wished to better match its future liabilities in employees’ salaries, which were assumed to rise with inflation. Hence, it entered into a series of 1 Inflation-indexed Derivatives inflation derivatives with Barclays Capital, in which it received a floating-rate, inflation-linked interest rate and paid nominal fixed- rate interest rate. The swaps ranged in maturity from 18 to 28 years, with a total notional amount of £300 million.
    [Show full text]