Vector Calculus
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 11. Three Dimensional Analytic Geometry and Vectors
Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1. -

An Introduction to Topology the Classification Theorem for Surfaces by E
An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5. -
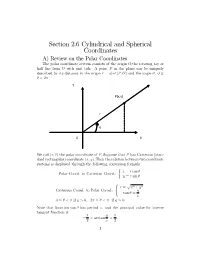
Section 2.6 Cylindrical and Spherical Coordinates
Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord. -

Area, Volume and Surface Area
The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 YEARS 810 Area, Volume and Surface Area (Measurement and Geometry: Module 11) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the international Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑NonCommercial‑NoDerivs 3.0 Unported License. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project MEASUREMENT AND GEOMETRY Module 11 AREA, VOLUME AND SURFACE AREA A guide for teachers - Years 8–10 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge YEARS 810 {4} A guide for teachers AREA, VOLUME AND SURFACE AREA ASSUMED KNOWLEDGE • Knowledge of the areas of rectangles, triangles, circles and composite figures. • The definitions of a parallelogram and a rhombus. • Familiarity with the basic properties of parallel lines. • Familiarity with the volume of a rectangular prism. • Basic knowledge of congruence and similarity. • Since some formulas will be involved, the students will need some experience with substitution and also with the distributive law. -

Analytic Geometry
STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you: -

Surface Topology
2 Surface topology 2.1 Classification of surfaces In this second introductory chapter, we change direction completely. We dis- cuss the topological classification of surfaces, and outline one approach to a proof. Our treatment here is almost entirely informal; we do not even define precisely what we mean by a ‘surface’. (Definitions will be found in the following chapter.) However, with the aid of some more sophisticated technical language, it not too hard to turn our informal account into a precise proof. The reasons for including this material here are, first, that it gives a counterweight to the previous chapter: the two together illustrate two themes—complex analysis and topology—which run through the study of Riemann surfaces. And, second, that we are able to introduce some more advanced ideas that will be taken up later in the book. The statement of the classification of closed surfaces is probably well known to many readers. We write down two families of surfaces g, h for integers g ≥ 0, h ≥ 1. 2 2 The surface 0 is the 2-sphere S . The surface 1 is the 2-torus T .For g ≥ 2, we define the surface g by taking the ‘connected sum’ of g copies of the torus. In general, if X and Y are (connected) surfaces, the connected sum XY is a surface constructed as follows (Figure 2.1). We choose small discs DX in X and DY in Y and cut them out to get a pair of ‘surfaces-with- boundaries’, coresponding to the circle boundaries of DX and DY. -
Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Differential Geometry of Curves and Surfaces 3
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES 3. Regular Surfaces 3.1. The definition of a regular surface. Examples. The notion of surface we are going to deal with in our course can be intuitively understood as the object obtained by a potter full of phantasy who takes several pieces of clay, flatten them on a table, then models of each of them arbitrarily strange looking pots, and finally glue them together and flatten the possible edges and corners. The resulting object is, formally speaking, a subset of the three dimensional space R3. Here is the rigorous definition of a surface. Definition 3.1.1. A subset S ⊂ R3 is a1 regular surface if for any point P in S one can find an open subspace U ⊂ R2 and a map ϕ : U → S of the form ϕ(u, v)=(x(u, v),y(u, v), z(u, v)), for (u, v) ∈ U with the following properties: 1. The function ϕ is differentiable, in the sense that the components x(u, v), y(u, v) and z(u, v) have partial derivatives of any order. 2 3 2. For any Q in U, the differential map d(ϕ)Q : R → R is (linear and) injective. 3. There exists an open subspace V ⊂ R3 which contains P such that ϕ(U) = V ∩ S and moreover, ϕ : U → V ∩ S is a homeomorphism2. The pair (U, ϕ) is called a local parametrization, or a chart, or a local coordinate system around P . Conditions 1 and 2 say that (U, ϕ) is a regular patch. -

Counting Essential Surfaces in 3-Manifolds
Counting essential surfaces in 3-manifolds Nathan M. Dunfield, Stavros Garoufalidis, and J. Hyam Rubinstein Abstract. We consider the natural problem of counting isotopy classes of es- sential surfaces in 3-manifolds, focusing on closed essential surfaces in a broad class of hyperbolic 3-manifolds. Our main result is that the count of (possibly disconnected) essential surfaces in terms of their Euler characteristic always has a short generating function and hence has quasi-polynomial behavior. This gives remarkably concise formulae for the number of such surfaces, as well as detailed asymptotics. We give algorithms that allow us to compute these generating func- tions and the underlying surfaces, and apply these to almost 60,000 manifolds, providing a wealth of data about them. We use this data to explore the delicate question of counting only connected essential surfaces and propose some con- jectures. Our methods involve normal and almost normal surfaces, especially the work of Tollefson and Oertel, combined with techniques pioneered by Ehrhart for counting lattice points in polyhedra with rational vertices. We also introduce arXiv:2007.10053v1 [math.GT] 20 Jul 2020 a new way of testing if a normal surface in an ideal triangulation is essential that avoids cutting the manifold open along the surface; rather, we use almost normal surfaces in the original triangulation. Contents 1 Introduction3 1.2 Main results . .4 1.5 Motivation and broader context . .5 1.7 The key ideas behind Theorem 1.3......................6 2 1.8 Making Theorem 1.3 algorithmic . .8 1.9 Ideal triangulations and almost normal surfaces . .8 1.10 Computations and patterns . -

Basics of the Differential Geometry of Surfaces
Chapter 20 Basics of the Differential Geometry of Surfaces 20.1 Introduction The purpose of this chapter is to introduce the reader to some elementary concepts of the differential geometry of surfaces. Our goal is rather modest: We simply want to introduce the concepts needed to understand the notion of Gaussian curvature, mean curvature, principal curvatures, and geodesic lines. Almost all of the material presented in this chapter is based on lectures given by Eugenio Calabi in an upper undergraduate differential geometry course offered in the fall of 1994. Most of the topics covered in this course have been included, except a presentation of the global Gauss–Bonnet–Hopf theorem, some material on special coordinate systems, and Hilbert’s theorem on surfaces of constant negative curvature. What is a surface? A precise answer cannot really be given without introducing the concept of a manifold. An informal answer is to say that a surface is a set of points in R3 such that for every point p on the surface there is a small (perhaps very small) neighborhood U of p that is continuously deformable into a little flat open disk. Thus, a surface should really have some topology. Also,locally,unlessthe point p is “singular,” the surface looks like a plane. Properties of surfaces can be classified into local properties and global prop- erties.Intheolderliterature,thestudyoflocalpropertieswascalled geometry in the small,andthestudyofglobalpropertieswascalledgeometry in the large.Lo- cal properties are the properties that hold in a small neighborhood of a point on a surface. Curvature is a local property. Local properties canbestudiedmoreconve- niently by assuming that the surface is parametrized locally. -

Analytic Geometry
INTRODUCTION TO ANALYTIC GEOMETRY BY PEECEY R SMITH, PH.D. N PROFESSOR OF MATHEMATICS IN THE SHEFFIELD SCIENTIFIC SCHOOL YALE UNIVERSITY AND AKTHUB SULLIVAN GALE, PH.D. ASSISTANT PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF ROCHESTER GINN & COMPANY BOSTON NEW YORK CHICAGO LONDON COPYRIGHT, 1904, 1905, BY ARTHUR SULLIVAN GALE ALL BIGHTS RESERVED 65.8 GINN & COMPANY PRO- PRIETORS BOSTON U.S.A. PEE FACE In preparing this volume the authors have endeavored to write a drill book for beginners which presents, in a manner conform- ing with modern ideas, the fundamental concepts of the subject. The subject-matter is slightly more than the minimum required for the calculus, but only as much more as is necessary to permit of some choice on the part of the teacher. It is believed that the text is complete for students finishing their study of mathematics with a course in Analytic Geometry. The authors have intentionally avoided giving the book the form of a treatise on conic sections. Conic sections naturally appear, but chiefly as illustrative of general analytic methods. Attention is called to the method of treatment. The subject is developed after the Euclidean method of definition and theorem, without, however, adhering to formal presentation. The advan- tage is obvious, for the student is made sure of the exact nature of each acquisition. Again, each method is summarized in a rule stated in consecutive steps. This is a gain in clearness. Many illustrative examples are worked out in the text. Emphasis has everywhere been put upon the analytic side, that is, the student is taught to start from the equation. -

Efficient Methods to Calculate Partial Sphere Surface Areas for A
Mathematical and Computational Applications Article Efficient Methods to Calculate Partial Sphere Surface Areas for a Higher Resolution Finite Volume Method for Diffusion-Reaction Systems in Biological Modeling Abigail Bowers, Jared Bunn and Myles Kim * Department of Applied Mathematics, Florida Polytechnic University, Lakeland, FL 33805, USA; abowers@floridapoly.edu (A.B.); jbunn@floridapoly.edu (J.B.) * Correspondence: mkim@floridapoly.edu Received: 14 November 2019; Accepted: 20 December 2019; Published: 23 December 2019 Abstract: Computational models for multicellular biological systems, in both in vitro and in vivo environments, require solving systems of differential equations to incorporate molecular transport and their reactions such as release, uptake, or decay. Examples can be found from drugs, growth nutrients, and signaling factors. The systems of differential equations frequently fall into the category of the diffusion-reaction system due to the nature of the spatial and temporal change. Due to the complexity of equations and complexity of the modeled systems, an analytical solution for the systems of the differential equations is not possible. Therefore, numerical calculation schemes are required and have been used for multicellular biological systems such as bacterial population dynamics or cancer cell dynamics. Finite volume methods in conjunction with agent-based models have been popular choices to simulate such reaction-diffusion systems. In such implementations, the reaction occurs within each finite volume and finite volumes interact with one another following the law of diffusion. The characteristic of the reaction can be determined by the agents in the finite volume. In the case of cancer cell growth dynamics, it is observed that cell behavior can be different by a matter of a few cell size distances because of the chemical gradient.