Red-Black Trees Are an Alternative to AVL Trees
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Trees • Binary Trees • Newer Types of Tree Structures • M-Ary Trees
Data Organization and Processing Hierarchical Indexing (NDBI007) David Hoksza http://siret.ms.mff.cuni.cz/hoksza 1 Outline • Background • prefix tree • graphs • … • search trees • binary trees • Newer types of tree structures • m-ary trees • Typical tree type structures • B-tree • B+-tree • B*-tree 2 Motivation • Similarly as in hashing, the motivation is to find record(s) given a query key using only a few operations • unlike hashing, trees allow to retrieve set of records with keys from given range • Tree structures use “clustering” to efficiently filter out non relevant records from the data set • Tree-based indexes practically implement the index file data organization • for each search key, an indexing structure can be maintained 3 Drawbacks of Index(-Sequential) Organization • Static nature • when inserting a record at the beginning of the file, the whole index needs to be rebuilt • an overflow handling policy can be applied → the performance degrades as the file grows • reorganization can take a lot of time, especially for large tables • not possible for online transactional processing (OLTP) scenarios (as opposed to OLAP – online analytical processing) where many insertions/deletions occur 4 Tree Indexes • Most common dynamic indexing structure for external memory • When inserting/deleting into/from the primary file, the indexing structure(s) residing in the secondary file is modified to accommodate the new key • The modification of a tree is implemented by splitting/merging nodes • Used not only in databases • NTFS directory structure -

Tree-Combined Trie: a Compressed Data Structure for Fast IP Address Lookup
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 12, 2015 Tree-Combined Trie: A Compressed Data Structure for Fast IP Address Lookup Muhammad Tahir Shakil Ahmed Department of Computer Engineering, Department of Computer Engineering, Sir Syed University of Engineering and Technology, Sir Syed University of Engineering and Technology, Karachi Karachi Abstract—For meeting the requirements of the high-speed impact their forwarding capacity. In order to resolve two main Internet and satisfying the Internet users, building fast routers issues there are two possible solutions one is IPv6 IP with high-speed IP address lookup engine is inevitable. addressing scheme and second is Classless Inter-domain Regarding the unpredictable variations occurred in the Routing or CIDR. forwarding information during the time and space, the IP lookup algorithm should be able to customize itself with temporal and Finding a high-speed, memory-efficient and scalable IP spatial conditions. This paper proposes a new dynamic data address lookup method has been a great challenge especially structure for fast IP address lookup. This novel data structure is in the last decade (i.e. after introducing Classless Inter- a dynamic mixture of trees and tries which is called Tree- Domain Routing, CIDR, in 1994). In this paper, we will Combined Trie or simply TC-Trie. Binary sorted trees are more discuss only CIDR. In addition to these desirable features, advantageous than tries for representing a sparse population reconfigurability is also of great importance; true because while multibit tries have better performance than trees when a different points of this huge heterogeneous structure of population is dense. -

Balanced Trees Part One
Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0. -

Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

Assignment 3: Kdtree ______Due June 4, 11:59 PM
CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension. -

Splay Trees Last Changed: January 28, 2017
15-451/651: Design & Analysis of Algorithms January 26, 2017 Lecture #4: Splay Trees last changed: January 28, 2017 In today's lecture, we will discuss: • binary search trees in general • definition of splay trees • analysis of splay trees The analysis of splay trees uses the potential function approach we discussed in the previous lecture. It seems to be required. 1 Binary Search Trees These lecture notes assume that you have seen binary search trees (BSTs) before. They do not contain much expository or backtround material on the basics of BSTs. Binary search trees is a class of data structures where: 1. Each node stores a piece of data 2. Each node has two pointers to two other binary search trees 3. The overall structure of the pointers is a tree (there's a root, it's acyclic, and every node is reachable from the root.) Binary search trees are a way to store and update a set of items, where there is an ordering on the items. I know this is rather vague. But there is not a precise way to define the gamut of applications of search trees. In general, there are two classes of applications. Those where each item has a key value from a totally ordered universe, and those where the tree is used as an efficient way to represent an ordered list of items. Some applications of binary search trees: • Storing a set of names, and being able to lookup based on a prefix of the name. (Used in internet routers.) • Storing a path in a graph, and being able to reverse any subsection of the path in O(log n) time. -

Binary Search Tree
ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is -

6.172 Lecture 19 : Cache-Oblivious B-Tree (Tokudb)
How TokuDB Fractal TreeTM Indexes Work Bradley C. Kuszmaul Guest Lecture in MIT 6.172 Performance Engineering, 18 November 2010. 6.172 —How Fractal Trees Work 1 My Background • I’m an MIT alum: MIT Degrees = 2 × S.B + S.M. + Ph.D. • I was a principal architect of the Connection Machine CM-5 super computer at Thinking Machines. • I was Assistant Professor at Yale. • I was Akamai working on network mapping and billing. • I am research faculty in the SuperTech group, working with Charles. 6.172 —How Fractal Trees Work 2 Tokutek A few years ago I started collaborating with Michael Bender and Martin Farach-Colton on how to store data on disk to achieve high performance. We started Tokutek to commercialize the research. 6.172 —How Fractal Trees Work 3 I/O is a Big Bottleneck Sensor Query Systems include Sensor Disk Query sensors and Sensor storage, and Query want to perform Millions of data elements arrive queries on per second Query recently arrived data using indexes. recent data. Sensor 6.172 —How Fractal Trees Work 4 The Data Indexing Problem • Data arrives in one order (say, sorted by the time of the observation). • Data is queried in another order (say, by URL or location). Sensor Query Sensor Disk Query Sensor Query Millions of data elements arrive per second Query recently arrived data using indexes. Sensor 6.172 —How Fractal Trees Work 5 Why Not Simply Sort? • This is what data Data Sorted by Time warehouses do. • The problem is that you Sort must wait to sort the data before querying it: Data Sorted by URL typically an overnight delay. -

Search Trees for Strings a Balanced Binary Search Tree Is a Powerful Data Structure That Stores a Set of Objects and Supports Many Operations Including
Search Trees for Strings A balanced binary search tree is a powerful data structure that stores a set of objects and supports many operations including: Insert and Delete. Lookup: Find if a given object is in the set, and if it is, possibly return some data associated with the object. Range query: Find all objects in a given range. The time complexity of the operations for a set of size n is O(log n) (plus the size of the result) assuming constant time comparisons. There are also alternative data structures, particularly if we do not need to support all operations: • A hash table supports operations in constant time but does not support range queries. • An ordered array is simpler, faster and more space efficient in practice, but does not support insertions and deletions. A data structure is called dynamic if it supports insertions and deletions and static if not. 107 When the objects are strings, operations slow down: • Comparison are slower. For example, the average case time complexity is O(log n logσ n) for operations in a binary search tree storing a random set of strings. • Computing a hash function is slower too. For a string set R, there are also new types of queries: Lcp query: What is the length of the longest prefix of the query string S that is also a prefix of some string in R. Prefix query: Find all strings in R that have S as a prefix. The prefix query is a special type of range query. 108 Trie A trie is a rooted tree with the following properties: • Edges are labelled with symbols from an alphabet Σ. -

Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke
Trees Trees, Binary Search Trees, Heaps & Applications Dr. Chris Bourke Department of Computer Science & Engineering University of Nebraska|Lincoln Lincoln, NE 68588, USA [email protected] http://cse.unl.edu/~cbourke 2015/01/31 21:05:31 Abstract These are lecture notes used in CSCE 156 (Computer Science II), CSCE 235 (Dis- crete Structures) and CSCE 310 (Data Structures & Algorithms) at the University of Nebraska|Lincoln. This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License 1 Contents I Trees4 1 Introduction4 2 Definitions & Terminology5 3 Tree Traversal7 3.1 Preorder Traversal................................7 3.2 Inorder Traversal.................................7 3.3 Postorder Traversal................................7 3.4 Breadth-First Search Traversal..........................8 3.5 Implementations & Data Structures.......................8 3.5.1 Preorder Implementations........................8 3.5.2 Inorder Implementation.........................9 3.5.3 Postorder Implementation........................ 10 3.5.4 BFS Implementation........................... 12 3.5.5 Tree Walk Implementations....................... 12 3.6 Operations..................................... 12 4 Binary Search Trees 14 4.1 Basic Operations................................. 15 5 Balanced Binary Search Trees 17 5.1 2-3 Trees...................................... 17 5.2 AVL Trees..................................... 17 5.3 Red-Black Trees.................................. 19 6 Optimal Binary Search Trees 19 7 Heaps 19 -
B-Trees M-Ary Search Tree Solution
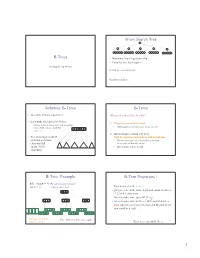
M-ary Search Tree B-Trees • Maximum branching factor of M • Complete tree has height = Section 4.7 in Weiss # disk accesses for find : Runtime of find : 2 Solution: B-Trees B-Trees • specialized M-ary search trees What makes them disk-friendly? • Each node has (up to) M-1 keys: 1. Many keys stored in a node – subtree between two keys x and y contains leaves with values v such that • All brought to memory/cache in one access! 3 7 12 21 x ≤ v < y 2. Internal nodes contain only keys; • Pick branching factor M Only leaf nodes contain keys and actual data such that each node • The tree structure can be loaded into memory takes one full irrespective of data object size {page, block } x<3 3≤x<7 7≤x<12 12 ≤x<21 21 ≤x • Data actually resides in disk of memory 3 4 B-Tree: Example B-Tree Properties ‡ B-Tree with M = 4 (# pointers in internal node) and L = 4 (# data items in leaf) – Data is stored at the leaves – All leaves are at the same depth and contain between 10 40 L/2 and L data items – Internal nodes store up to M-1 keys 3 15 20 30 50 – Internal nodes have between M/2 and M children – Root (special case) has between 2 and M children (or root could be a leaf) 1 2 10 11 12 20 25 26 40 42 AB xG 3 5 6 9 15 17 30 32 33 36 50 60 70 Data objects, that I’ll Note: All leaves at the same depth! ignore in slides 5 ‡These are technically B +-Trees 6 1 Example, Again B-trees vs. -

AVL Trees and Rotations
/ AVL trees and rotations Q1 Operations (insert, delete, search) are O(height) Tree height is O(log n) if perfectly balanced ◦ But maintaining perfect balance is O(n) Height-balanced trees are still O(log n) ◦ For T with height h, N(T) ≤ Fib(h+3) – 1 ◦ So H < 1.44 log (N+2) – 1.328 * AVL (Adelson-Velskii and Landis) trees maintain height-balance using rotations Are rotations O(log n)? We’ll see… / or = or \ Different representations for / = \ : Just two bits in a low-level language Enum in a higher-level language / Assume tree is height-balanced before insertion Insert as usual for a BST Move up from the newly inserted node to the lowest “unbalanced” node (if any) ◦ Use the balance code to detect unbalance - how? Do an appropriate rotation to balance the sub-tree rooted at this unbalanced node For example, a single left rotation: Two basic cases ◦ “See saw” case: Too-tall sub-tree is on the outside So tip the see saw so it’s level ◦ “Suck in your gut” case: Too-tall sub-tree is in the middle Pull its root up a level Q2-3 Unbalanced node Middle sub-tree attaches to lower node of the “see saw” Diagrams are from Data Structures by E.M. Reingold and W.J. Hansen Q4-5 Unbalanced node Pulled up Split between the nodes pushed down Weiss calls this “right-left double rotation” Q6 Write the method: static BalancedBinaryNode singleRotateLeft ( BalancedBinaryNode parent, /* A */ BalancedBinaryNode child /* B */ ) { } Returns a reference to the new root of this subtree.