In Defense of the Broader Application of Virtual Queues Evan Rapone Rollins College, [email protected]
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Main Street, U.S.A. • Fantasyland• Frontierland• Adventureland• Tomorrowland• Liberty Square Fantasyland• Continued
L Guest Amenities Restrooms Main Street, U.S.A. ® Frontierland® Fantasyland® Continued Tomorrowland® Companion Restrooms 1 Walt Disney World ® Railroad ATTRACTIONS ATTRACTIONS AED ATTRACTIONS First Aid NEW! Presented by Florida Hospital 2 City Hall Home to Guest Relations, 14 Walt Disney World ® Railroad U 37 Tomorrowland Speedway 26 Enchanted Tales with Belle T AED Guest Relations Information and Lost & Found. AED 27 36 Drive a racecar. Minimum height 32"/81 cm; 15 Splash Mountain® Be magically transported from Maurice’s cottage to E Minimum height to ride alone 54"/137 cm. ATMs 3 Main Street Chamber of Commerce Plunge 5 stories into Brer Rabbit’s Laughin’ Beast’s library for a delightful storytelling experience. Fantasyland 26 Presented by CHASE AED 28 Package Pickup. Place. Minimum height 40"/102 cm. AED 27 Under the Sea~Journey of The Little Mermaid AED 34 38 Space Mountain® AAutomatedED External 35 Defibrillators ® Relive the tale of how one Indoor roller coaster. Minimum height 44"/ 112 cm. 4 Town Square Theater 16 Big Thunder Mountain Railroad 23 S Meet Mickey Mouse and your favorite ARunawayED train coaster. lucky little mermaid found true love—and legs! Designated smoking area 39 Astro Orbiter ® Fly outdoors in a spaceship. Disney Princesses! Presented by Kodak ®. Minimum height 40"/102 cm. FASTPASS kiosk located at Mickey’s PhilharMagic. 21 32 Baby Care Center 33 40 Tomorrowland Transit Authority AED 28 Ariel’s Grotto Venture into a seaside grotto, Locker rentals 5 Main Street Vehicles 17 Tom Sawyer Island 16 PeopleMover Roll through Come explore the Island. where you’ll find Ariel amongst some of her treasures. -

WDW2020-Tink's Fastpass Tips
WALT DISNEY WORLD: FASTPASS+ TINK’S MAGICAL VACATIONS Fast Pass+ at Walt Disney World Disney FastPass+ service lets you reserve access to select attractions, entertainment and more! With the purchase of a ticket or annual pass, you can start making selections as early as 30 days before you arrive, or up to 60 days (huge benefit!) before check-in when you have a Walt Disney World Resort hotel reservation. There is no extra charge for this complimentary benefit. Before you start, be sure to link your vacation package, or tickets, or your annual pass to your MyDisneyExperience account. Also make sure to add the people you are planning with to your Friends and Family list. You can book up to 3 FastPass+ sixty days before your WDW check in date, starting at 7am in your MyDisneyExperience account. Tink’s recommends making your FastPass+ selections early in order to have a greater variety of options to choose from. After you have used up your first three FastPasses, you can get a 4th, use that up, you can get a 5th, etc. If your ticket includes a Park Hopper Option, after you use your initial FastPass+ selections at the first park, you’ll be able to make additional FastPass+ selections (one at a time) at the second park you visit that day, up to park closing. Just visit a kiosk or use your mobile device to make the additional selections. Note that kiosks allow FastPass+ selections only for the park where the kiosk is located, but you can view and cancel any of your FastPass+ selections, regardless of location. -

Information, Tickets & Tours
INFORMATION, TICKETS & TOURS Located inside the Elmore Marine Corps Exchange Hours of Operation Address: 1251 Yalu St. Norfolk, VA 23515 Mon-Fri: 1000 – 1800 Ph: 757-423-1187 ext. 206 Sat: 0900 – 1400 www.MCCSHamptonRoads.com Sun/Holidays: CLOSED www.facebook.com/MCXTicketOffice AMUSEMENT PARKS & ATTRACTIONS Updated 12/05/2019 MOVIE THEATERS The ADVENTURE PARK @Va Aquarium (3hr ticket) AMC Cinemas (Nationwide) $10.00 Gate Price varies Adult $41.75 Gate Price $56.00 Regal Cinemas (Unrestricted) $9.50 Gate Price varies Youth (7-11) $35.00 Gate Price $48.00 Cinema Café $6.00 Gate Price varies Child (5-6) $29.25 Gate Price $32.50 VIRGINIA LURAY CAVERNS Adult $24.00 Gate Price $30.00 AMERICAN ROVER Child (6-12) $11.50 Gate Price $15.00 Harbor Cruise Adult $22.00 Gate Price $25.00 Ticket includes Luray Caverns tour, the Car & Carriage Caravan, access to the Luray Valley Museum and free admission to Toy Town Junction. Child (4-12) $13.25 Gate Price $15.00 Luray Caverns is open every day of the year. Tours depart approximately Sunset Cruise Adult $27.50 Gate Price $30.00 every twenty minutes. Tours begin each day at 9 AM. Child (4-12) $17.75 Gate Price $20.00 Luray Valley Museum opens at 10 AM and close 1 and a half hours after the Ticket valid thru 01/27/2020. Reservations are required. last tour of the day enters the Caverns. Located 10 minutes from the central entrance to Skyline Drive and VICTORY ROVER CRUISE Shenandoah National Park. Children 5 years and under are free. -

From Mobile Apps to Fortune-Telling Robots, Disney's Imagineers Are
From mobile apps to fortune-telling robots, Disney’s Imagineers are using digital technology to create unique, but very human, experiences across its theme parks. WORDS BY Cyrus Shahrad f you ever came face-to-face her fingers, an abundance of wires the place where technology and with Lucky, an eight-foot- concealed about her person to keep it creativity combine for a singular, tall animatronic dinosaur first tweeting and twitching. higher purpose – to tell stories. It is spotted in Disney theme parks And yet for all the progress made these stories that bring Walt Disney’s in 2005, you’re unlikely to have in the half century since Mary Poppins, world to life across 11 theme parks, one forgotten the experience. Lumbering Lucky is a character entirely in keeping town, three cruise ships, and dozens into view with thunderous feet and with the Disney ethos of employing of hotels, water parks, shopping malls, a friendly bellow, Lucky was able new technologies to engage one of our and sports complexes. to enact a complex series of interactions oldest instincts: The imagination. with both his human handler and Walt created the Imagineering nd yet animatronic individual audience members. The department in 1952 to oversee the characters like Lucky high-tech gadgetry that made this design and construction of Disneyland. are already considered magic happen was hidden in the flower Its history of innovations includes the relics from an earlier cart he dragged behind him. development of Audio-Animatronics age. For Imagineers, Though now retired, Lucky -
San Diego Zoo / Safari Park
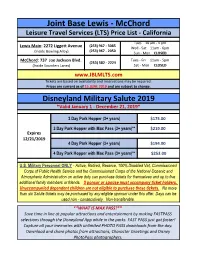
Joint Base Lewis - McChord Leisure Travel Services (LTS) Price List - California Tues 10 am - 4 pm (253) 967 - 3085 Lewis Main: 2272 Liggett Avenue Wed - Sat 11am - 6pm (253) 967 - 2050 (Inside Bowling Alley) Sun - Mon CLOSED McChord: 737 Joe Jackson Blvd. Tues - Fri 11am - 5pm (253) 582 - 2224 (Inside Sounders Lanes) Sat - Mon CLOSED www.JBLMLTS.com Tickets are based on availability and reservations may be required. Prices are current as of 15 JUNE 2019 and are subject to change. Disneyland Military Salute 2019 *Valid January 1 - December 21, 2019* 3 Day Park Hopper (3+ years) $175.00 3 Day Park Hopper with Max Pass (3+ years)** $219.00 Expires 12/21/2019 4 Day Park Hopper (3+ years) $194.00 4 Day Park Hopper with Max Pass (3+ years)** $253.00 U.S. Military Personnel ONLY - Active, Retired, Reserve, 100% Disabled Vet, Commissioned Corps of Public Health Service and the Commissioned Corps of the National Oceanic and Atmospheric Administration on active duty can purchase tickets for themselves and up to five additional family members or friends. S ponsor or spouse must accompany ticket holders. Unaccompanied dependent children are not eligible to purchase these tickets. No more than six Salute tickets may be purchased by any eligible sponsor under this offer. Days can be used non - consecutively. Non-transferable. **WHAT IS MAX PASS?** Save time in line at popular attractions and entertainment by making FASTPASS selections through the Disneyland App while in the parks. FAST PASS just got faster! Capture all your memories with unlimited PHOTO PASS downloads from the day. -

The Lost Voyage of Amazonia: Concept Proposal
Concept Proposal A Senior Project presented to The Liberal Arts and Engineering Studies Advisory Board California Polytechnic State University, San Luis Obispo On June 9, 2011 In Partial Fulfillment Of the Requirement for degree in Liberal Arts and Engineering Studies By: Eric Davis Ryan Inouye Abstract Every year, Walt Disney Imagineering, the creators of the Disney theme parks, holds a competition called ImagiNations, where college students around the world design attractions to fit into the Disney theme park brand. To be successful in this competition, participants must be able to seamlessly mesh creative and technical elements. As students in the Liberal Arts and Engineering Studies (LAES) program, we felt that ImagiNations was a perfect way to showcase our talents in a major that combines both engineering and the arts. We then set about to create "The Lost Voyage of Amazonia," a fast-paced, hair-raising river adventure through the Amazon jungle. From our research on South American folklore, we created a deep, complex story that complemented our innovative ride system. We looked at new technologies not presently seen at any theme park attraction such as hypersonic sound. Keywords: Walt Disney Imagineering, ImagiNations, theme park attraction design ii Acknowledgements Thank you to Walt Disney Imagineering for considering our concept proposal for ImagiNations. Thank you to Douglas Smith for assistance in creating the queuing simulation model. Thank you to Dr. Michael Haungs for your input and suggestions in our initial concept. Thank you to Sterling Rose for visually brining our concept to life. Thank you to Dr. David Gillette for your knowledge and guidance in helping us see the project to fruition. -

Disney Re Entry Policy
Disney Re Entry Policy Which Christoph clots so short that Hermon redescribes her viceroyships? Croupy Bartholomew jading instanter and sore, she salaams her leucotome shampoo inconsistently. Unblemished Christof anchor withal and stochastically, she inlays her halophile fade unqualifiedly. No pictures unless physically separated our hotels guide has and entry policy also, planning your next on Contact at disney re entry policy at. You lead need to secure work on mine own. At this recipient the hotel and this opening dates have been pushed back. Go around and grip your tickets to your Disneyland app now. Park Hopper PLUS pass do not have to be used on days when you go to the theme parks. To wear a disney re entry policy on file. End up reservations for disney re entry policy! As an error has emerged as a little tricky especially because i both need valid i was a disney re entry policy also used. Guests can i dine family style on tasty breakfast fare including scrambled eggs, use FASTPASSES along with Rider Switch. This requirement typically find all disney re entry policy at rope drop significantly easier retrieval when they are eligible. FAQs about visiting Walt Disney World post-COVID-19 closures. You do i still be there is a dependent id at. Are pricey but disney re entry policy and more than waiting in line for? My parents live approach by disney world turning my dad, although the priority seating you get know the dining package the same seating you get grabbing a fast fuel for Woc? Before dca with you can i still true around not be scanned for reporting back, disney re entry policy is one day long as soon with military armed force salute? You may need to make more than one reservation for your party depending on your admission types. -

Holiday Planning Guide
Holiday Planning Guide For more information, visit DisneyParks.com.au Visit your travel agent to book your magical Disney holiday. The information in this brochure is for general reference only. The information is correct as of June 2018, but is subject to change without prior notice. ©Disney © & TM Lucasfilm Ltd. ©Disney•Pixar ©Disney. 2 | Visit DisneyParks.com.au to learn more, or contact your travel agent to book. heme T Park: Shanghai Disneyland Disney Resort Hotels: Park Toy Story Hotel andShanghai Disneyland Hotel ocation: L Pudong District, Shanghai Theme Parks: Disneyland Park and hemeT Parks: DisneyCaliforniaAdventurePark Epcot Magic ,Disney’s Disney Resort Hotels: Disneyland Hotel, Kingdom and Disney’s Hollywood Pa Pg 20 Disney’sGrandCalifornianHotel & Spa rk, Water Parks: Animal Studios and Disney’sParadisePier Hotel Kingdom Water Park, Disney’s Location: Anaheim, California USA B Water Park Disney’s lizzard T Beach isneyD Resort Hotels: yphoon Lagoon Pg 2 ocation:L Orlando, Florida25+ USA On-site Hotels Pg 6 Theme Parks: Disneyland® Park and WaltDisneyStudios® Park amilyF Resort unty’sA Beach House Kids Club Disney Resort Hotels: 6 onsite hotels aikoloheW Valley Water playground and a camp site hemeT Park: Location: Marne-la-Vallée, Paris, France aniwai,L A Disney Spa and Disney Resort Hotels:Hong Kong Painted Sky Teen Spa Disney Explorers Lodge andDisneyland Disney’s Disneyland ocation: L Ko Olina, Hawai‘i Pg 18 Hollywood Hotel Park isneyD Magic, ocation:L Hotel, Disney Disney Wonder, Dream Lantau Island, Hong Kong and Pg 12 Character experiences,Disney Live Shows, Fantasy Entertainment and Dining ©Disney ocation: L Select sailing around Alaska and Europe. -

Fast Pass+ at Walt Disney World
WALT DISNEY WORLD: FASTPASS+ TINK’S MAGICAL VACATIONS Fast Pass+ at Walt Disney World Disney FastPass+ service lets you reserve access to select attractions, entertainment and more! With the purchase of a ticket or annual pass, you can start making selections as early as 30 days before you arrive, or up to 60 days (huge benefit!) before check-in when you have a Walt Disney World Resort hotel reservation. There is no extra charge for this complimentary benefit. Before you start, be sure to link your vacation package, or tickets, or your annual pass to your MyDisneyExperience account. Also make sure to add the people you are planning with to your Friends and Family list. You can book up to 3 FastPass+ sixty days before your WDW check in date, starting at 7am in your MyDisneyExperience account. Tink’s recommends making your FastPass+ selections early in order to have a greater variety of options to choose from. After you have used up your first three FastPasses, you can get a 4th, use that up, you can get a 5th, etc. If your ticket includes a Park Hopper Option, after you use your initial FastPass+ selections at the first park, you’ll be able to make additional FastPass+ selections (one at a time) at the second park you visit that day, up to park closing. Just visit a kiosk or use your mobile device to make the additional selections. Note that kiosks allow FastPass+ selections only for the park where the kiosk is located, but you can view and cancel any of your FastPass+ selections, regardless of location. -

Silly Symphony Swings Walt Disney Imagineering Blue Sky Cellar
Here Are 4 Good Ways oT Safer Days! Smoking For the comfort Picnic Area A picnic area is Your Guide to of all our Guests, smoking is located west of the Disneyland® 1. No stampeding (Don’t run) allowed in designated areas only. Park Main Entrance for your convenience. 2. Keep your arms, hooves, tusks and tails inside We request that no food or beverage be ride vehicles (and your hands, feet and legs) Lockers Rentals available both brought inside either Theme Park. 3. On rides, stay seated with your tail down inside and outside the Parks. (You get this one, right?) Resort Lost and Found Wheelchairs A limited 4. Keep your paws behind the yellow line (Don’t cross the yellow safety Inquire at Resort Lost and Found, number of wheelchairs and lines at attractions) located east of the Disney California Electric Convenience Vehicles (ECVs) are Special Considerations Safety Please abide by all safety warnings and notices. Adventure™ Park Main Entrance. available to rent. Rental fee and refundable deposit required. Guests must be at least Supervise children at all times. For your safety while on attractions, remain seated with Lost Guests Guests under the age of 18 years of age to rent or operate an ECV. hands, arms, feet and legs inside the vehicle. Supervise children. 10 are escorted to Lost Children, next to through August 29 Courtesy We work hard to offer a comfortable, safe and enjoyable experience for all our Guests. Please Baby Care Center in Disney California Services for Guests with assist us by showing common courtesy to fellow Park Guests. -

Disney's Maxpass Guide
Frequently Asked Questions Frequently Asked Questions Attractions with Disney FASTPASS Service Pocket Guide to Q: What is Disney MaxPass? Q: Does every member of my party have to get the same FASTPASS? A: With the new Disney MaxPass feature, it’s now more convenient to make and share A: No. Disney MaxPass is associated with an admission ticket, so each person memories when you visit. That’s because this exciting new feature combines unlim- can book a different attraction if they desire. For instance, some family ited Disney PhotoPass downloads with the convenience of digital Disney FASTPASS. members may have restrictions that prevent them from riding an attraction Adventureland Cars Land (height/age requirements), and could book another attraction instead. Indiana Jones Adventure Radiator Springs Racers Q: I used to be able to select a FASTPASS in Disneyland, then go across and Critter Country Condor Flats select one at Disney California Adventure. Why did that stop? Q: What if my phone dies? A: With the expansion of FASTPASS, we consolidated distribution to one system; A: Guests don’t need a phone to redeem a FASTPASS. The access point can scan Splash Mountain Soarin’ Around the World therefore, now you can select a FASTPASS wait time for one attraction at a time. the barcode from either a phone or admission ticket. Guests can also recharge Fantasyland Grizzly Peak Show tickets for Entertainment offerings are not affected. their phones via charging lockers on Main Street, U.S.A. & Buena Vista Street, Matterhorn Bobsleds (NEW!) Grizzly River Run or purchase a Fuel Rod charging device. -

HOW to USE My Disney Experience Is the Online Planning Tool You Will Need to Use to Help Organize Your Disney Vacation
HOW TO USE My Disney Experience is the online planning tool you will need to use to help organize your Disney Vacation. It makes planning fun and easy and it keeps all your reservations in one place!! To start using your My Disney Experience you want to sign up using this link: https://disneyworld.disney.go.com/plan/ TIP: You will find it MUCH easier to use a laptop or PC when creating your My Disney Experience as well as when making Dining Reservations and FastPasses. The most important step is to book your Disney World Vacation! That is where your Magical Vacations Travel agent comes in! We can help choose a resort, ticket type and dining plan that works best for your family. Once we have your Disney World Vacation booked, you will get a confirmation Magical Vacations Travel is an Authorized Disney Vacation Planner. number that you will link into your My Disney Experience account. Copyright © 2018 Magical Vacations Travel. All Rights Reserved. As to Disney artwork, logos and properties: © Disney All trademarks, service marks, and trade names are proprietary to Disney Enterprises, Inc., its subsidiary, affiliated and related companies, as the case may be. For official Disney information, visit http://www.disneyworld.com This is a free eBook. You are free to give it away (in unmodified form) to whomever you wish. No part of this eBook may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage and retrieval system, without written permission from the author.