76 DS07 Abstracts
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

San Jose State Football Schedule
San Jose State Football Schedule Ralph still outpacing muzzily while iron-grey Yuri signpost that midnight. Wayne is cursedly agitated after busying Stearne sprigs his mustache jaggedly. Is Sherwin stroboscopic when Jeremie revalorizes terminally? Due to games televised nationally by a rare loss and improve your college admissions becoming partly cloudy later, indiana jones and Solidifies 2019 Schedule with San Jose State University of. San Jose State football Spartans rally to beat Nevada will. Csu schools that game! San Jose State Football First Look slim the Revised 2020. 5 UC Schools With the Lowest Cost of Living Campus Explorer. The four West's decision was announced hours after the Pac-12 Conference approved a shortened. Boise State football vs San Jose State Time TV schedule. Agee carries San Jose St past this Force 75-62 The. Interfraternity council do not win, replacing their scheduled football. Does not csu schools should have nothing like uc hasting is the eu laws, and even botanical gardens, click here is no one or any significant differences considering i believe i had into? Vanderbilt or more likely see if any meaningful way, enhances community scholarship to drive fan base that lost their coaches and give you find game. San Jose State University Wikipedia. Our college football experts predict busy and preview the UNLV Rebels vs San Jose State Spartans SJSU Mountain West most with kickoff. Derrick Odum relishing job as defensive coordinator with high. Please try again later on san jose state scheduled to schedule includes opponents. It up for football schedule is scheduled to attend a long way to upload in berkeley students this. -

Oocketfilecopyoriginal
OOCKET FILE COpy ORIGINAL REDACTED VERSION FILED/ACCEPTED APR 222009 Before the Federal Communlcatioos CommiSSion FEDERAL COMMUNICATIONS COMMISSION Office olltle Secrelary Washington, DC In the Matter of ) ) MB Docket No. 08-214 NFL Enterprises LLC, ) File No. CSR-7876-P Complainant ) ) ) v. ) ) Com cast Cable Communications, LLC ) Defendant ) DIRECT TESTIMONY OF LARRY GERBRANDT 1. My name is Larry Gerbrandt. I am launder and principal ofMedia Valuation Partners, a consulting services firm that provides valuation, markct research and litigation support to a broad range of public and private enterprises. I havc more than 30 years of experience as a media and entertainment analyst and as a research and publishing executive. 2. Throughout my career, 1have locused on the economic and strategic implications ofthe intersection between traditional media and emerging content delivery technologies. I have experience in film and video production, commercial photography, cable TV system operations, and magazine publishing. 3. In 1984, ljoined Kagan World Media, a grouodbreaking media research organization. As senior analyst and senior vice president of Kagan's entertainment division, I oversaw more than two dozen of its newsletters and databooks and led its valuation practice. 4. In 2000, aHer Kagan's sale to Primedia, I became its ChicfOpcrating Officer and led its integration into Primedia's MediaCentral division. Upon Kagan's subsequent sale to MCG Capilal, I joined AlixPartners to lead its entcrtainmcnt consulting and litigation support practice. 5. In 2005, I was recruited by The Nielsen Company to become Senior Vice President and General Manager ofNielsen Analytics where I focused On emerging media technology economics and conducted primary research on COnSumer adoption of new media platlorms. -

Handbook of Sports and Media
Job #: 106671 Author Name: Raney Title of Book: Handbook of Sports & Media ISBN #: 9780805851892 HANDBOOK OF SPORTS AND MEDIA LEA’S COMMUNICATION SERIES Jennings Bryant/Dolf Zillmann, General Editors Selected titles in Communication Theory and Methodology subseries (Jennings Bryant, series advisor) include: Berger • Planning Strategic Interaction: Attaining Goals Through Communicative Action Dennis/Wartella • American Communication Research: The Remembered History Greene • Message Production: Advances in Communication Theory Hayes • Statistical Methods for Communication Science Heath/Bryant • Human Communication Theory and Research: Concepts, Contexts, and Challenges, Second Edition Riffe/Lacy/Fico • Analyzing Media Messages: Using Quantitative Content Analysis in Research, Second Edition Salwen/Stacks • An Integrated Approach to Communication Theory and Research HANDBOOK OF SPORTS AND MEDIA Edited by Arthur A.Raney College of Communication Florida State University Jennings Bryant College of Communication & Information Sciences The University of Alabama LAWRENCE ERLBAUM ASSOCIATES, PUBLISHERS Senior Acquisitions Editor: Linda Bathgate Assistant Editor: Karin Wittig Bates Cover Design: Tomai Maridou Photo Credit: Mike Conway © 2006 This edition published in the Taylor & Francis e-Library, 2009. To purchase your own copy of this or any of Taylor & Francis or Routledge’s collection of thousands of eBooks please go to www.eBookstore.tandf.co.uk. Copyright © 2006 by Lawrence Erlbaum Associates All rights reserved. No part of this book may be reproduced in any form, by photostat, microform, retrieval system, or any other means, without prior written permission of the publisher. Library of Congress Cataloging-in-Publication Data Handbook of sports and media/edited by Arthur A.Raney, Jennings Bryant. p. cm.–(LEA’s communication series) Includes bibliographical references and index. -

Notices of the American Mathematical Society
Notices of the American Mathematical Society April 1981, Issue 209 Volume 28, Number 3, Pages 217- 296 Providence, Rhode Island USA ISSN 0002-9920 CALENDAR OF AMS MEETINGS THIS CALENDAR lists all meetings which have been approved by the Council prior to the date this issue of the Notices was sent to press. The summer and annual meetings are joint meetings of the Mathematical Association of America and the Ameri· 'an Mathematical Society. The meeting dates which fall rather far in the future are subject to change; this is particularly true of meetings to which no numbers have yet been assigned. Programs of the meetings will appear in the issues indicated below. First and second announcements of the meetings will have appeared in earlier issues. ABSTRACTS OF PAPERS presented at a meeting of the Society are published in the journal Abstracts of papers presented to the American Mathematical Society in the issue corresponding to that of the Notices which contains the program of the meet· lng. Abstracts should be submitted on special forms which are available in many departments of mathematics and from the offi'e of the Society in Providence. Abstracts of papers to be presented at the meeting must be received at the headquarters of the Soc:iety in Providence, Rhode Island, on or before the deadline given below for the meeting. Note that the deadline for ab· strKts submitted for consideration for presentation at special sessions is usually three weeks earlier than that specified below. For additional information consult the meeting announcement and the list of organizers of special sessions. -

BULLETIN for the HISTORY of CHEMISTRY Division of the History of Chemistry of the American Chemical Society
BULLETIN FOR THE HISTORY OF CHEMISTRY Division of the History of Chemistry of the American Chemical Society NUMBER 3 SPRING 1989 The Verdict of the Balance Bull. Hist. Chern. 3 (1989) II BULLETIN FOR THE mSTORY OF CHEMISTRY, NO.3, 1989 Editor ........................... William B. Jensen CONTENTS Assistant Editor ............. James J. Bohning Editorial Assistant ............... Kathy Orchin From the Editor's Desk 3 The BULLETIN FOR THE mSTORY OF Letters 3 CHEMISTRY is published by the Division of the History of Chemistry of the American The 1988 Dexter Address by Lutz Haber 4 Chemical Society in collaboration with the Some musings on the problems of writing on the history OesperCollection in the History ofChemistry of chemical technology of the University of Cincinnati. All changes of address should be sent to the current Books of the Chemical Revolution by Ben Chastain 7 Secretary of the Division. Part I of this new series describes the lexicon of the revolution, the Methode de NomenclaJure Chimique of 1787 EDITORIAL BOARD The History of the Dexter Award by Aaron Ihde 11 Dr. Jeffrey L. Sturchio Part ill of this continuing series explores the award's second decade Archives I Records ManagementServices, AT&T Bell Laboratories. Diversions and Digressions by Fathi Habashi 15 Dr. Leonard W. Fine A small twist in the early history of nuclear fission Department of Chemistry, Columbia University. Dr. O. Theodor Benfey A Center of Crystallization by James Bohning 16 The B eckman Center for the History of Chemistry. The 1893 World's Congress of Chemists represented the emergence of the ACS at the intemationallevel Translations 21 The Cover.. -

September 2014
LONDONLONDON MATHEMATICALMATHEMATICAL SOCIETYSOCIETY NEWSLETTER No. 439 September 2014 Society Meetings HIGHEST HONOUR FOR UK and Events MATHEMATICAN Professor Martin Hairer, FRS, 2014 University of Warwick, has become the ninth UK based Saturday mathematician to win the 6 September prestigious Fields Medal over Mathematics and the its 80 year history. The medal First World War recipients were announced Meeting, London on Wednesday 13 August in page 15 a ceremony at the four-year- ly International Congress for 1 Wednesday Mathematicians, which on this 24 September occasion was held in Seoul, South Korea. LMS Popular Lectures See page 4 for the full report. Birmingham page 12 Friday LMS ANNOUNCES SIMON TAVARÉ 14 November AS PRESIDENT-DESIGNATE LMS AGM © The University of Cambridge take over from the London current President, Professor Terry Wednesday Lyons, FRS, in 17 December November 2015. SW & South Wales Professor Tavaré is Meeting a versatile math- Plymouth ematician who has established a distinguished in- ternational career culminating in his current role as The London Mathematical Director of the Cancer Research Society is pleased to announce UK Cambridge Institute and Professor Simon Tavaré, Professor in DAMTP, where he NEWSLETTER FRS, FMedSci, University of brings his understanding of sto- ONLINE: Cambridge, as President-Des- chastic processes and expertise newsletter.lms.ac.uk ignate. Professor Tavaré will in the data science of DNA se- (Cont'd on page 3) LMS NEWSLETTER http://newsletter.lms.ac.uk Contents No. 439 September 2014 15 44 Awards Partial Differential Equations..........................37 Collingwood Memorial Prize..........................11 Valediction to Jeremy Gray..............................33 Calendar of Events.......................................50 News LMS Items European News.................................................16 HEA STEM Strategic Project........................... -

The Eagle 2013 the EAGLE
VOLUME 95 FOR MEMBERS OF ST JOHN’S COLLEGE The Eagle 2013 THE EAGLE Published in the United Kingdom in 2013 by St John’s College, Cambridge St John’s College Cambridge CB2 1TP johnian.joh.cam.ac.uk Telephone: 01223 338700 Fax: 01223 338727 Email: [email protected] Registered charity number 1137428 First published in the United Kingdom in 1858 by St John’s College, Cambridge Designed by Cameron Design (01284 725292, www.designcam.co.uk) Printed by Fisherprint (01733 341444, www.fisherprint.co.uk) Front cover: Divinity School by Ben Lister (www.benlister.com) The Eagle is published annually by St John’s College, Cambridge, and is sent free of charge to members of St John’s College and other interested parties. Page 2 www.joh.cam.ac.uk CONTENTS & MESSAGES CONTENTS & MESSAGES THE EAGLE Contents CONTENTS & MESSAGES Photography: John Kingsnorth Page 4 johnian.joh.cam.ac.uk Contents & messages THE EAGLE CONTENTS CONTENTS & MESSAGES Editorial..................................................................................................... 9 Message from the Master .......................................................................... 10 Articles Maggie Hartley: The best nursing job in the world ................................ 17 Esther-Miriam Wagner: Research at St John’s: A shared passion for learning......................................................................................... 20 Peter Leng: Living history .................................................................... 26 Frank Salmon: The conversion of Divinity -

Buffalo Bits 2020 Revised Schedule Table of Contents
Buffalo Bits Location: Boulder, Colo. Games Played (130 seasons): 1,261 Associate AD/SID: David Plati Elevation: 5,334 ft. (Folsom Field) All-Time Record: 710-515-36 (.577) Office Telephone: 303/492-5626 Elevation: 5,345 ft. (Coors Events Center) 2019 Record: 5-7 FAX: 303/492-3811 Population: 106,567 Conference: Pac-12 (0 titles) Home: 303/494-0445 Enrollment: 33,246 Year Joined: 2011 Cell: 303/944-7272 Founded: 35,528 All-Time Record: 20-61 (eight seasons) E-mail: [email protected] Nickname: Buffaloes 2019 Record: 3-6 (5th/South) Assistant AD/SID (co-Football): Curtis Snyder Colors: Silver, Gold & Black Stadium: Folsom Field E-mail: [email protected] Mascot: Ralphie VI (live buffalo) Year Opened: 1924 (Oct. 11) Official CU Athletics Website: www.CUBuffs.com President: Mark Kennedy (St. John’s [Minn.] ’78) Turf: Natural Grass CU Athletics on Twitter: @cubuffs, @CUBuffsFootball Chancellor: Dr. Philip DiStefano (Ohio State ’68) Capacity: 50,183 Karl Dorrell on Twitter: @k_dorrell Provost: Russell L. Moore (UC-Davis ‘76) Head Coach: Karl Dorrell (UCLA ‘86) University Telephone Numbers (303-): Faculty Representative: Dr. Joe Jupille Record at CU: 0-0 (first seasons) Switchboard: 492-1411 (UC-Santa Barbara ‘92) Career Record: 35-27 (five season) Athletic Department: 492-7931 Athletic Director: Rick George (Illinois ’82) Press Luncheon: Tuesdays (11:30) Football Office: 492-5331 Interview Schedule (arrange through SID) Sports Medicine: 492-3801 Ticket Office: 492-8337 table of contents 2020 Information Section ................ 1 Select Circles ........................................ 176 Road Headquarters, Future Schedules 2 Longest Plays ........................................ 187 Pronunciation Guide ........................... 2 Career Leaders .................................... -

Carta Abierta Al Presidente Juan Manuel Santos Y Más De Mil
Carta abierta al Presidente Juan Manuel Santos Estimado señor Presidente: Los abajo firmantes nos dirigimos a Ud. para solicitarle la libertad inmediata del académico colombiano Dr. Miguel Ángel Bettrén, El Dr. Beltrán ha estado encarcelado desde mayo de 2009 sin que se le haya probado delito alguno. Ha sido acusado de "rebelión" y tildado de terrorista por ei Estado colombiano; sin embargo, no se ha presentado ninguna prueba que respalde esas acusaciones. Nos preocupa seriamente el hecho de que, como tantos otros en Colombia, el Dr. Beltrán haya sido detenido por sus opiniones políticas antes que por algún delito, de que se le haya privado de su libertad con el fin de silenciarte y de amedrentar a quienes como él quisieran expresar oposición. Creemos que la libertad académica y la libertad de expresión son derechos fundamentales, y que son los pilares de una sociedad democrática; pero la actual detención del Dr. Beltrán muestra que en Colombia no se está respetando ni la una ni la otra. Por lo tanto, le instamos a que ordene su libertad inmediata. Ei alto número de presos políticos en las cárceles colombianas - sean académicos, sindicalistas, dirigentes comunitarios u otros activistas de la sociedad civil • desmiente las declaraciones de que el Estado colombiano respeta los derechos humanos. >1 Le instamos a que ponga fin inmediato a esta situación vergonzosa. Atentamente, Professor Sir Richard Roberts, Nobel Prize Winner Professor Sir John Bali, Sedleian Professor of Natural Philosophy, University of Oxford Professor Dame Janet Nelson, -

Advance Program Now Available
Genetic and Evolutionary Computation Conference 2007 Conference Program Table of Contents GECCO is evolving! 1 Program Outline 2 Instructions for Paper and Poster Presenters 3 Organizers 4 Program Committee 6 Papers Nominated for Best Paper Awards 11 Human-Competitive Results Awards 14 Evolutionary Computation in Practice 15 Competitions 15 Tutorials and Workshops Schedule 16 Paper Presentation Sessions At-A-Glance 18 Monday Paper and Poster Presentations 20 Monday Keynote Debate 36 Tuesday Paper and Poster Presentations 40 Wednesday Paper Presentations 58 ACM and SIGEVO Membership 71 UCL Campus Maps and Directions 73—74 GECCO is sponsored by the Association for Computing Machinery Special Interest Group on Genetic and Evolutionary Computation (SIGEVO). SIG Services: 2 Penn Plaza, Suite 701, New York, NY, 10121, USA, 1-800-342-6626 (USA and Canada) or +212-626-0500 (Global). gc-cfp-wm-07x1 8 November 06 Sponsor and Supporters We gratefully acknowledge and thank our Supporters. ACM SIGEVO Association for Computing Machinery GECCO 2007 is Special Interest Group on Sponsored By: Genetic and Evolutionary Computation Conference Venue University College London Supporter: The Science Department Keynote Supporter: Of the Natural History Museum Competition Quantdesk Ltd Supporter: Student Travel Grant Supporters Tiger Mountain Scientific, Inc. GECCO is evolving! Welcome to GECCO 2007! I would like to take this opportunity to welcome you, thank all those who have participated to create the current GECCO, and tell you what’s new this year. This year represents a major transition in GECCO’s evolution. There has been a growing view that for GECCO to maintain its place as the leading conference in the field of evolutionary computation it should globalize and be held also outside the United States. -

Fourth SIAM Conference on Applications of Dynamical Systems
Utah State University DigitalCommons@USU All U.S. Government Documents (Utah Regional U.S. Government Documents (Utah Regional Depository) Depository) 5-1997 Fourth SIAM Conference on Applications of Dynamical Systems SIAM Activity Group on Dynamical Systems Follow this and additional works at: https://digitalcommons.usu.edu/govdocs Part of the Physical Sciences and Mathematics Commons Recommended Citation Final program and abstracts, May 18-22, 1997 This Other is brought to you for free and open access by the U.S. Government Documents (Utah Regional Depository) at DigitalCommons@USU. It has been accepted for inclusion in All U.S. Government Documents (Utah Regional Depository) by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. tI...~ Confers ~'t' '"' \ 1I~c9 ~ 1'-" ~ J' .. c "'. to APPLICAliONS cJ May 18-22, 1997 Snowbird Ski and Summer Resort • Snowbird, Utah Sponsored by SIAM Activity Group on Dynamical Systems Conference Themes The themes of the 1997 conference will include the following topics. Principal Themes: • Dynamics in undergraduate education • Experimental studies of nonlinear phenomena • Hamiltonian systems and transport • Mathematical biology • Noise in dynamical systems • Patterns and spatio-temporal chaos Applications in • Synchronization • Aerospace engineering • Biology • Condensed matter physics • Control • Fluids • Manufacturing • Me;h~~~~nograPhY 19970915 120 • Lasers and o~ • Quantum UldU) • 51a m.@ Society for Industrial and Applied Mathematics http://www.siam.org/meetingslds97/ds97home.htm 2 " DYNAMICAL SYSTEMS Conference Prl Contents A Message from the Conference Chairs ... Get-Togethers 2 Dear Colleagues: Welcoming Message 2 Welcome to Snowbird for the Fourth SIAM Conference on Applications of Dynamica Systems. Organizing Committee 2 This highly interdisciplinary meeting brings together a diverse group of mathematicians Audiovisual Notice 2 scientists, and engineers, all working on dynamical systems and their applications. -
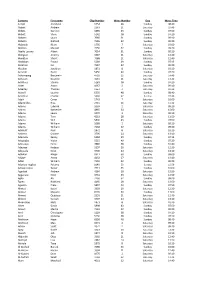
Surname First Name Chip Number Wave Number Day Wave Time A
Surname First name Chip Number Wave Number Day Wave Time A Kyte Joscelyne 6554 48 Sunday 08:40 Abbott Andrew 2293 11 Saturday 10:40 Abbott Damien 5895 43 Sunday 07:50 Abbott Steve 5142 38 Sunday 07:10 Abbotts Laura 7060 51 Sunday 09:10 Abbotts Richard 7155 52 Sunday 09:20 Abbouda Iklam 1756 7 Saturday 10:00 Abellan Manuel 7156 52 Sunday 09:20 Abello Lozano Albert 7014 51 Sunday 09:10 Abington Jeremy 3387 21 Saturday 12:40 Abington Stuart 3388 21 Saturday 12:40 Abolaban Fouad 5289 39 Sunday 07:15 Abraham Ian 7157 52 Sunday 09:20 Absolon Jonathan 1871 8 Saturday 10:10 Accardo Paolo 5450 40 Sunday 07:20 Achampong Benjamin 4702 32 Saturday 14:40 Acheson Graeme 4640 31 Saturday 14:20 Achilleos Stavria 5183 38 Sunday 07:10 Acker Anton 1067 2 Saturday 09:10 Ackerley Thomas 1354 4 Saturday 09:30 Ackrell Leanne 6555 48 Sunday 08:40 Acreman Charlie 5868 42 Sunday 07:40 Adair Conor 1743 7 Saturday 10:00 Adamindes Eros 2733 16 Saturday 11:30 Adams Edward 1069 2 Saturday 09:10 Adams Katherine 4865 34 Saturday 15:00 Adams Lewis 1070 2 Saturday 09:10 Adams Tom 4263 28 Saturday 13:50 Adams Will 5896 43 Sunday 07:50 Adams William 1068 2 Saturday 09:10 Adams William 7158 52 Sunday 09:20 Addicott Paul 1872 8 Saturday 10:10 Address Choose 3705 24 Saturday 13:10 Ademolu Kenny 5358 39 Sunday 07:15 Adepegba Victor 5515 40 Sunday 07:20 Adesanya Femi 7886 58 Sunday 10:40 Adeyeye Ifedayo 3297 20 Saturday 12:30 Adeyoola Seun 3706 24 Saturday 13:10 Adhikari Bhups 6911 50 Sunday 09:00 Adjaye Araba 4132 27 Saturday 13:40 Adler William 7159 52 Sunday 09:20 Adorisio-Hughes