Stability of Ring Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

JUICE Red Book
ESA/SRE(2014)1 September 2014 JUICE JUpiter ICy moons Explorer Exploring the emergence of habitable worlds around gas giants Definition Study Report European Space Agency 1 This page left intentionally blank 2 Mission Description Jupiter Icy Moons Explorer Key science goals The emergence of habitable worlds around gas giants Characterise Ganymede, Europa and Callisto as planetary objects and potential habitats Explore the Jupiter system as an archetype for gas giants Payload Ten instruments Laser Altimeter Radio Science Experiment Ice Penetrating Radar Visible-Infrared Hyperspectral Imaging Spectrometer Ultraviolet Imaging Spectrograph Imaging System Magnetometer Particle Package Submillimetre Wave Instrument Radio and Plasma Wave Instrument Overall mission profile 06/2022 - Launch by Ariane-5 ECA + EVEE Cruise 01/2030 - Jupiter orbit insertion Jupiter tour Transfer to Callisto (11 months) Europa phase: 2 Europa and 3 Callisto flybys (1 month) Jupiter High Latitude Phase: 9 Callisto flybys (9 months) Transfer to Ganymede (11 months) 09/2032 – Ganymede orbit insertion Ganymede tour Elliptical and high altitude circular phases (5 months) Low altitude (500 km) circular orbit (4 months) 06/2033 – End of nominal mission Spacecraft 3-axis stabilised Power: solar panels: ~900 W HGA: ~3 m, body fixed X and Ka bands Downlink ≥ 1.4 Gbit/day High Δv capability (2700 m/s) Radiation tolerance: 50 krad at equipment level Dry mass: ~1800 kg Ground TM stations ESTRAC network Key mission drivers Radiation tolerance and technology Power budget and solar arrays challenges Mass budget Responsibilities ESA: manufacturing, launch, operations of the spacecraft and data archiving PI Teams: science payload provision, operations, and data analysis 3 Foreword The JUICE (JUpiter ICy moon Explorer) mission, selected by ESA in May 2012 to be the first large mission within the Cosmic Vision Program 2015–2025, will provide the most comprehensive exploration to date of the Jovian system in all its complexity, with particular emphasis on Ganymede as a planetary body and potential habitat. -

Planetary Rings
CLBE001-ESS2E November 10, 2006 21:56 100-C 25-C 50-C 75-C C+M 50-C+M C+Y 50-C+Y M+Y 50-M+Y 100-M 25-M 50-M 75-M 100-Y 25-Y 50-Y 75-Y 100-K 25-K 25-19-19 50-K 50-40-40 75-K 75-64-64 Planetary Rings Carolyn C. Porco Space Science Institute Boulder, Colorado Douglas P. Hamilton University of Maryland College Park, Maryland CHAPTER 27 1. Introduction 5. Ring Origins 2. Sources of Information 6. Prospects for the Future 3. Overview of Ring Structure Bibliography 4. Ring Processes 1. Introduction houses, from coalescing under their own gravity into larger bodies. Rings are arranged around planets in strikingly dif- Planetary rings are those strikingly flat and circular ap- ferent ways despite the similar underlying physical pro- pendages embracing all the giant planets in the outer Solar cesses that govern them. Gravitational tugs from satellites System: Jupiter, Saturn, Uranus, and Neptune. Like their account for some of the structure of densely-packed mas- cousins, the spiral galaxies, they are formed of many bod- sive rings [see Solar System Dynamics: Regular and ies, independently orbiting in a central gravitational field. Chaotic Motion], while nongravitational effects, includ- Rings also share many characteristics with, and offer in- ing solar radiation pressure and electromagnetic forces, valuable insights into, flattened systems of gas and collid- dominate the dynamics of the fainter and more diffuse dusty ing debris that ultimately form solar systems. Ring systems rings. Spacecraft flybys of all of the giant planets and, more are accessible laboratories capable of providing clues about recently, orbiters at Jupiter and Saturn, have revolutionized processes important in these circumstellar disks, structures our understanding of planetary rings. -

Planetary Ring Dynamics - Matthew Hedman
CELESTIAL MECHANICS - Planetary Ring Dynamics - Matthew Hedman PLANETARY RING DYNAMICS Matthew Hedman University of Idaho, Moscow ID, U.S.A. Keywords: celestial mechanics, disks, dust, orbits, perturbations, planets, resonances, rings, solar system dynamics Contents 1. Introduction to Planetary Ring Systems 2. Orbital Perturbations on Individual Ring Particles 3. Inter-particle Interactions 4. External Perturbations on Dense Rings 5. Conclusions Acknowledgements Glossary Bibliography Biographical Sketch Summary Planetary rings provide a natural laboratory for investigating dynamical phenomena. Thanks to their proximity to Earth, the rings surrounding the giant planets can be studied at high resolution and in great detail. Indeed, Earth-based observations and spacecraft missions have documented a diverse array of structures in planetary rings produced by both inter-particle interactions and various external perturbations. These features provide numerous opportunities to examine the detailed dynamics of particle- rich disks, and can potentially provide insights into other astrophysical disk systems like galaxies and proto-planetary disks. This chapter provides a heuristic introduction to the dynamics of the known planetary rings. We begin by reviewing the basic architecture of the four known ring systems surrounding the giant planets. Then we turn our attention to the types of dynamical phenomena observed in the various rings. First, we consider how different forces can modify the orbital properties of individual ring particles. Next, we investigate the patterns and textures generated within a ring by the interactions among the ring particles. Finally, we discuss how these two types of processes can interact to produce structures in dense planetary rings. 1. Introduction to Planetary Ring Systems Ring systems surround all four of the giant planets in the outer solar system. -

Scientific Goals for Exploration of the Outer Solar System
Scientific Goals for Exploration of the Outer Solar System Explore Outer Planet Systems and Ocean Worlds OPAG Report v. 28 August 2019 This is a living document and new revisions will be posted with the appropriate date stamp. Outline August 2019 Letter of Response to Dr. Glaze Request for Pre Decadal Big Questions............i, ii EXECUTIVE SUMMARY ......................................................................................................... 3 1.0 INTRODUCTION ................................................................................................................ 4 1.1 The Outer Solar System in Vision and Voyages ................................................................ 5 1.2 New Emphasis since the Decadal Survey: Exploring Ocean Worlds .................................. 8 2.0 GIANT PLANETS ............................................................................................................... 9 2.1 Jupiter and Saturn ........................................................................................................... 11 2.2 Uranus and Neptune ……………………………………………………………………… 15 3.0 GIANT PLANET MAGNETOSPHERES ........................................................................... 18 4.0 GIANT PLANET RING SYSTEMS ................................................................................... 22 5.0 GIANT PLANETS’ MOONS ............................................................................................. 25 5.1 Pristine/Primitive (Less Evolved?) Satellites’ Objectives ............................................... -

Origin and Evolution of Saturn's Ring System
Origin and Evolution of Saturn’s Ring System Chapter 17 of the book “Saturn After Cassini-Huygens” Saturn from Cassini-Huygens, Dougherty, M.K.; Esposito, L.W.; Krimigis, S.M. (Ed.) (2009) 537-575 Sébastien CHARNOZ * Université Paris Diderot/CEA/CNRS Paris, France Luke DONES Southwest Research Institute Colorado, USA Larry W. ESPOSITO University of Colorado Colorado, USA Paul R. ESTRADA SETI Institute California, USA Matthew M. HEDMAN Cornell University New York, USA (*): to whom correspondence should be addressed : [email protected] 1 ABSTRACT: The origin and long-term evolution of Saturn’s rings is still an unsolved problem in modern planetary science. In this chapter we review the current state of our knowledge on this long- standing question for the main rings (A, Cassini Division, B, C), the F Ring, and the diffuse rings (E and G). During the Voyager era, models of evolutionary processes affecting the rings on long time scales (erosion, viscous spreading, accretion, ballistic transport, etc.) had suggested that Saturn’s rings are not older than 10 8 years. In addition, Saturn’s large system of diffuse rings has been thought to be the result of material loss from one or more of Saturn’s satellites. In the Cassini era, high spatial and spectral resolution data have allowed progress to be made on some of these questions. Discoveries such as the “propellers” in the A ring, the shape of ring-embedded moonlets, the clumps in the F Ring, and Enceladus’ plume provide new constraints on evolutionary processes in Saturn’s rings. At the same time, advances in numerical simulations over the last 20 years have opened the way to realistic models of the rings’ fine scale structure, and progress in our understanding of the formation of the Solar System provides a better-defined historical context in which to understand ring formation. -

Moons and Rings
The Rings of Saturn 5.1 Saturn, the most beautiful planet in our solar system, is famous for its dazzling rings. Shown in the figure above, these rings extend far into space and engulf many of Saturn’s moons. The brightest rings, visible from Earth in a small telescope, include the D, C and B rings, Cassini’s Division, and the A ring. Just outside the A ring is the narrow F ring, shepherded by tiny moons, Pandora and Prometheus. Beyond that are two much fainter rings named G and E. Saturn's diffuse E ring is the largest planetary ring in our solar system, extending from Mimas' orbit to Titan's orbit, about 1 million kilometers (621,370 miles). The particles in Saturn's rings are composed primarily of water ice and range in size from microns to tens of meters. The rings show a tremendous amount of structure on all scales. Some of this structure is related to gravitational interactions with Saturn's many moons, but much of it remains unexplained. One moonlet, Pan, actually orbits inside the A ring in a 330-kilometer-wide (200-mile) gap called the Encke Gap. The main rings (A, B and C) are less than 100 meters (300 feet) thick in most places. The main rings are much younger than the age of the solar system, perhaps only a few hundred million years old. They may have formed from the breakup of one of Saturn's moons or from a comet or meteor that was torn apart by Saturn's gravity. -

Jupiter's Ring-Moon System
11 Jupiter’s Ring-Moon System Joseph A. Burns Cornell University Damon P. Simonelli Jet Propulsion Laboratory Mark R. Showalter Stanford University Douglas P. Hamilton University of Maryland Carolyn C. Porco Southwest Research Institute Larry W. Esposito University of Colorado Henry Throop Southwest Research Institute 11.1 INTRODUCTION skirts within the outer stretches of the main ring, while Metis is located 1000 km closer to Jupiter in a region where the ∼ Ever since Saturn’s rings were sighted in Galileo Galilei’s ring is depleted. Each of the vertically thick gossamer rings early sky searches, they have been emblematic of the ex- is associated with a moon having a somewhat inclined orbit; otic worlds beyond Earth. Now, following discoveries made the innermost gossamer ring extends towards Jupiter from during a seven-year span a quarter-century ago (Elliot and Amalthea, and exterior gossamer ring is connected similarly Kerr 1985), the other giant planets are also recognized to be with Thebe. circumscribed by rings. Small moons are always found in the vicinity of plane- Jupiter’s diaphanous ring system was unequivocally de- tary rings. Cuzzi et al. 1984 refer to them as “ring-moons,” tected in long-exposure images obtained by Voyager 1 (Owen while Burns 1986 calls them “collisional shards.” They may et al. 1979) after charged-particle absorptions measured by act as both sources and sinks for small ring particles (Burns Pioneer 11 five years earlier (Fillius et al. 1975, Acu˜na and et al. 1984, Burns et al. 2001). Ness 1976) had hinted at its presence. The Voyager flybys also discovered three small, irregularly shaped satellites— By definition, tenuous rings are very faint, implying Metis, Adrastea and Thebe in increasing distance from that particles are so widely separated that mutual collisions Jupiter—in the same region; they joined the similar, but play little role in the evolution of such systems. -

Science from the Jupiter Europa Orbiter—A Future Outer Planet Flagship Mission
Exploring Europa: Science from the Jupiter Europa Orbiter—A Future Outer Planet Flagship Mission Louise M. Prockter, Kenneth E. Hibbard, Thomas J. Magner, and John D. Boldt he Europa Jupiter System Mission, an international joint mission recently studied by NASA and the European Space Agency, would directly address the origin and evolution of satellite systems and the water-rich environ- ments of icy moons. In this article, we report on the scientific goals of the NASA-led part of the Europa Jupiter System Mission, the Jupiter Europa Orbiter, which would investigate the potential habitability of the ocean-bearing moon Europa by character- izing the geophysical, compositional, geological, and external processes that affect this icy world. INTRODUCTION About 400 years ago Galileo Galilei discovered the continued in 1994 with the arrival of the Galileo space- four large moons of Jupiter, thereby spurring the Coper- craft. After dropping a probe into Jupiter’s atmosphere, nican Revolution and forever changing our understand- the spacecraft spent several years orbiting the giant ing of the universe. Today, these Galilean satellites planet, accomplishing flybys of all the Galilean satellites, may hold the key to understanding the habitability of Io, Europa, Ganymede, and Callisto. Despite significant icy worlds, as three of the moons are believed to harbor technical setbacks, including the loss of the main com- internal oceans. On Earth, water is the key ingredient munication antenna and issues with the onboard tape for life, so it is reasonable that the search for life in our recorder, the spacecraft returned valuable data that sig- solar system should focus on the search for water. -
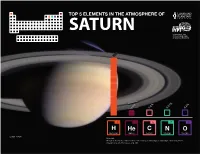
Top 5 Elements in the Atmosphere of Saturn
TOP 5 ELEMENTS IN THE ATMOSPHERE OF SATURN 10% 0.3% 0.01% 0.3% 1 2 6 7 8 H He C N O Hydrogen Helium Carbon Nitrogen Oxygen Credit: NASA Sources: Atreya et al. (2018). Saturn in the 21st century, Cambridge: Cambridge University Press. Cavalié et al. (2017). Icarus, Vol. 291. SATURN DR.THIBAULTFrench National Center for Research CAVALIÉ (CNRS) Saturn is the second largest planet in the solar system, after Jupiter, and is the only planet that is less dense than water. It is a gas giant, in the sense that most of its mass is made of gas. Its observable atmosphere comprises about 90% hydrogen and 10% helium. Other elements like carbon and nitrogen are present in traces (about 0.3% and 0.01%, respectively). One of the great Dr. Thibault Cavalié is a planetary mysteries, however, resides in the deep composition of the planet, which scientist for the French National Center remains largely unknown. It is likely that Saturn’s interior contains lots of water, for Research (CNRS) at Laboratoire and thus oxygen, possibly at the same proportion as helium. An atmospheric d’Astrophysique de Bordeaux in Pessac, probe plunging deep in the planet could unveil the bulk composition of Saturn France. He is also affiliated with the and enable scientists to better understand its formation. Saturn has been Laboratoire d’Etudes Spatiales et visited by four spacecraft so far — Pioneer 11, Voyagers 1 and 2, and Cassini d’Instrumentation en Astrophysique — but none of them probed the deep layers of the planet. Among other (LESIA) of the Paris Observatory. -

Our Planets at a Glance
made startling new discoveries. Our Planets But the past 20 years have been the golden age of planetary exploration. Advancements in rocketry during the 1950s enabled mankind's machines to At a Glance break the grip of Earth's gravity and travel to the Moon and to other J'!)lanets. { From our watery world we have gazed upon the American expeditions have explored the Moon, cosmic oeean for untold thousands of years. The our robot craft have landed on and reported from ancient astronomers observed' points of light the surfaces of Venus and Mars, our spacecraft which appeared to wander among the stars. They have orbited and provided much information about called these objects planets, which means wan Mars and Venus, and have made cl0se ran@e derers, and named them after great mythological ebservations while flying past Mereu. Jupiter, deities-Jupiter, king of the Roman gods; Mars, and Saturn. the Roman god of war; Mercury, messenger of the These voyagers brought a quantum leap in our gods; Venus, the Roman god of love and beauty; knowledge and uneerstanding of the solar system. and Saturn, father of Jupiter and god of Througn the electronic sight and otliler "senses" agriGulture. of our automated probes, color and eomplexion Science flourished during the European Renais have been given to worlds that existed for cen sance. Fundamental physical laws governing turies as fuzzy disks or indistinct points ef light. planetary motion were discovered and the orbits Future historians will likely. view these pioneer of the planets around the Sun were calculated. In ing flights to the planets as one of the most the 17th Century, astr:onomers pointed a new remarkable human achievements of the 20th device called the telescoJl)e at the heavens and Century. -

Computer Simulation of Saturn's Ring Structure
Computer Simulation of Saturn’s Ring Structure New Mexico Supercomputing Challenge Final Report April 3, 2013 Team 58 Los Alamos High School Team Members Cole Kendrick Teachers Brian Kendrick Project Mentor Brian Kendrick Summary The main goal of this project is to develop a computer program to model the creation of structure in Saturn’s ring system. The computer program will be used to answer these questions: (1) How are gaps in Saturn’s Rings formed; (2) how accurately can I model gap formation with a 3D N-Body simulation; and (3) will my simulation compare to observed features, theoretical data, and professional simulations. Newton’s laws of motion and gravity as well as the velocity Verlet method are being used to orbit the particles around Saturn. Gaps in Saturn’s ring system are caused by three main methods: (1) Gravitational resonances; (2) moons that orbit inside the ring; and (3) an asteroid or comet impact. Gravitational resonances are a major part of formation in the ring system, and are caused by a special ratio of orbits between a moon and a ring particle. Many different simulations were run to determine which moons are responsible for which gaps in the ring system. A patch method was developed in order to get a high particle density which allows for more accurate results. Many professionals are using a rotating patch method which achieves the same thing, however my patch method is unique and very easy compared to the rotating method. A simulation that involved an asteroid impact was run to determine the effects on the ring system. -

The Rings of Jupiter I
6 The Rings of Jupiter I. DE PATER, D. P. HAMILTON, M. R. SHOWALTER, H. B. THROOP, AND J. A. BURNS Book Chapter with optical depth τ ≈ a few×10−6 1; b) the toroidal-shaped `halo ring' interior to the main ring, which is a radially con- This is Chapter 6 in: Planetary Ring Systems, Eds. M. S. fined torus of faint material with τ ≈ 10−6; and c) the two Tiscareno and C. D. Murray. Cambridge University Press, faint `gossamer rings' coinciding with the orbits of Amalthea Cambridge, UK. In Press (2017) and Thebe (both τ ∼ 10−7; Figure 6.1, Table 6.1) . This version is free to view and download for per- It is believed that the rings' optical depth is dominated sonal use only. Not for re-distribution, re-sale or use by small grains (radius r < λ, with λ the observing wave- in derivative works. Copyright: Cambridge Univer- length), which are produced by collisions or interactions with sity Press. For more information on the book, see: larger parent bodies ( r ≥ λ, and perhaps up to hundreds of www.cambridge.org/9781107113824. meters in size). These parent bodies have not been individ- ually seen, but their existence is indirectly inferred by the rings' existence, and directly by measurements of the rings' phase curve and spectrum. Since the jovian ring system is extremely faint, it is chal- 6.1 Introduction lenging to determine its precise structure and the nature of the ring particles. Information on the rings' physical proper- The jovian ring was discovered as the result of a concerted ties can be derived by obtaining data over a range of phase search by the Voyager 1 cameras as the spacecraft passed angles α and wavelength λ; inversion of these spectra and Jupiter on March 4, 1979 (Smith et al., 1979b).