Proceedings of the Switched Power Workshop
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Design, Synthesis, Photochemical and Biological Evaluation of Novel Photoactive Molecular Switches
TESIS DOCTORAL Título Design, Synthesis, Photochemical and Biological Evaluation of Novel Photoactive Molecular Switches Autor/es David Martínez López Director/es Diego Sampedro Ruiz y Pedro José Campos García Facultad Facultad de Ciencia y Tecnología Titulación Departamento Química Curso Académico Design, Synthesis, Photochemical and Biological Evaluation of Novel Photoactive Molecular Switches, tesis doctoral de David Martínez López, dirigida por Diego Sampedro Ruiz y Pedro José Campos García (publicada por la Universidad de La Rioja), se difunde bajo una Licencia Creative Commons Reconocimiento-NoComercial- SinObraDerivada 3.0 Unported. ̉ Permisos que vayan más allá de lo cubierto por esta licencia pueden solicitarse a los titulares del copyright. © El autor © Universidad de La Rioja, Servicio de Publicaciones, 2019 publicaciones.unirioja.es E-mail: [email protected] Facultad de Ciencia y Tecnología Departamento de Química Área de Química Orgánica Grupo de Fotoquímica Orgánica TESIS DOCTORAL DESIGN, SYNTHESIS, PHOTOCHEMICAL AND BIOLOGICAL EVALUATION OF NOVEL PHOTOACTIVE MOLECULAR SWITCHES Memoria presentada en la Universidad de La Rioja para optar al grado de Doctor en Química por: David Martínez López Junio 2019 Facultad de Ciencia y Tecnología Departamento de Química Área de Química Orgánica Grupo de Fotoquímica Orgánica D. DIEGO SAMPEDRO RUIZ, Profesor Titular de Química Orgánica del Departamento de Química de la Universidad de La Rioja, y D. PEDRO JOSÉ CAMPOS GARCÍA, Catedrático de Química Orgánica del Departamento de Química de la Universidad de La Rioja. CERTIFICAN: Que la presente memoria, titulada “Design, synthesis, photochemical and biological evaluation of novel photoactive molecular switches”, ha sido realizada en el Departamento de Química de La Universidad de La Rioja bajo su dirección por el Licenciado en Química D. -
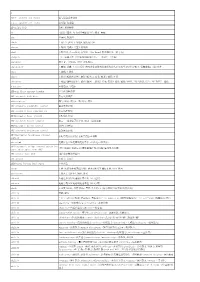
A A&C.P.=Anchors and Chains 锚与锚链试验合格a.A.R.=Against All Risks
A A&C.P.=anchors and chains 锚与锚链试验合格 a.a.r.=against all risks 综合险,保全险 AB=anchor bolt 锚栓,系紧螺栓 ab- (前缀)(厘米-克-秒CGS电磁制单位)绝对,电磁 abac 坐标网,列线图 aback 1.向后2.逆帆.3.停船4.使船向后退 abacus 1.顶板,冠板2.算盘3.列线图 abaft 在船尾部,在---后面,向船尾;~the beam在船正横以后(的方向) abampere (A)电磁安培(CGS电磁制电流单位,=10安培=1毕奥) abandoner 放弃者,弃船者;SHIP~弃船船员, abandonment 1.弃船,放弃.2.(商)委付(将残余保险物权转移给保险人以领取全部赔偿金额)3.放弃货载4.(油)废井 abase 1.落帆.2.降旗 abate 1.减退(指潮或水位),缓和(指风)2.废除,撤消3.减价,还价 abatement 1.减退(指潮或水位),缓和(指风) ,抑制2.作废,撤消3.减价,减税;NOISE ~噪声抑制,消声;~OF TAXES 减税 A-battery 丝极电池,甲电池 ABB=air-blast circuit breaker 空气吹弧断路器 ABB=automatic back bias 自动反馈偏压 abbreviation 缩写,略语,简号2.(数)约分,简化 ABC=automatic bandwidth control 自动带宽控制 ABC=automatic bias compensation 自动偏压补偿 ABC=automatic bias control 自动偏压控制 ABC=automatic binary computer 自动 二进制电子计算机,自动二进制电脑 ABC=automatic boiler control 锅炉自动控制 ABC=automatic brightness control 自动亮度控制 ABCC=automatic brightness contrast 自动亮度对比控制,自动亮度反差调整 control abcoulomb 电磁库仑(CGS电磁制电荷单位,=10库仑=1毕奥秒) ABCU=automatic bridge control system for (美国船级社船级标志)驾驶室遥控无人机舱(注明无人时限) unattended engine room (ABS) ABD=advance base dock (美)前沿基地浮船坞 abd=aboard 在船上,去船上 ABDC=after bottom dead center 下死点后 abeam 正横(与船的中线面成直角),横向;OBJECT~物标正横;WIND~横风 aberration 1.像差2.光行差3.偏差,反常 abfarad 电磁法拉(CGS电磁制电容单位=10-9法拉) abhenry 电磁亨利(CGS电磁制电感单位=10-9亨利) abide 1.忍受(风浪),坚持顶浪2.等待(其它船)3.(商行船被风浪所阻(海损用词) ability 性能,能力 ability ~of righting(船舶)扶正能力,复原能力;~to deposit weld熔敷焊接能力;~to self-stow自收藏能力(的); ability absorbing~吸收能力;accelerating~加速性能; ability adaptive~自适应能力;adhesive~粘着性; ability armour-penetrating~穿甲性;cargo-carrying~载货性能,载货能力; ability climbing~(垫)爬坡能力;course-chanhing~改(变)航(向)性(能);转首性(能) -

Enlightening Materials with Photoswitches
REVIEW www.advmat.de Enlightening Materials with Photoswitches Alexis Goulet-Hanssens,* Fabian Eisenreich,* and Stefan Hecht* reversible conversion between their stable Incorporating molecular photoswitches into various materials provides and (meta)stable isomers triggered by unique opportunities for controlling their properties and functions with high light. The return to their native, thermo spatiotemporal resolution using remote optical stimuli. The great and largely dynamically most stable isomer is gener ally induced by using another wavelength still untapped potential of these photoresponsive systems has not yet been of light or simply by heat, depending on fully exploited due to the fundamental challenges in harnessing geometrical the thermal stability of the (meta)stable and electronic changes on the molecular level to modulate macroscopic and isomer. Retinal—the prototypical photo bulk material properties. Herein, progress made during the past decade in switch in biology—showcases impressively the field of photoswitchable materials is highlighted. After pointing to some how structural changes occurring during a lightinduced doublebond isomerization general design principles, materials with an increasing order of the integrated can lead to vision or allow microorganisms photoswitchable units are discussed, spanning the range from amorphous to convert photons into metabolic energy. settings over surfaces/interfaces and supramolecular ensembles, to liquid In analogy, over the years, scientists have crystalline and crystalline phases. Finally, some potential future directions are learned that the lightdriven isomeriza pointed out in the conclusion. In view of the exciting recent achievements tion of small molecules can be collected, in the field, the future emergence and further development of light-driven possibly amplified, and transformed into macroscopic property changes, such as and optically programmable (inter)active materials and systems are eagerly mechanical motion,[1] charge carrying anticipated. -

Preface About Sunfounder Sunfounder Is a Technology Company Focused on Raspberry Pi and Arduino Open Source Community Development
Preface About SunFounder SunFounder is a technology company focused on Raspberry Pi and Arduino open source community development. Committed to the promotion of open source culture, we strive to bring the fun of electronics making to people all around the world and enable everyone to be a maker. Our products include learning kits, development boards, robots, sensor modules and development tools. In addition to high quality products, SunFounder also offers video tutorials to help you build your own project. If you have interest in open source or making something cool, welcome to join us! Visit www.sunfounder.com for more! About Sensor Kit V1.0 This kit is suitable for SunFounder Uno, SunFounder Mega 2560, SunFounder Duemilanove and SunFounder Nano. All the code in this user manual is compatible with these boards. Our SunFounder board is fully compatible with Arduino board. You can go to our official website www.sunfounder.com to download related code by clicking LEARN -> Get Tutorials. If you have any questions, please send an email to [email protected]. Also welcome to leave a message and share your projects on our FORUM. Note: This kit is different from other kits. All the components in this kit are provided in the form of modules which integrate some necessary components, such as comparator, resistor, and capacitor and so on. Therefore it is convenient for circuit connection. SunFounder Reprint 2.0 Contents Components List ................................................................................................................................. -

A Look at Video Binders 18 Daetron 29 Cameras, Vcrs, and a Sound Converter
*.4 October 1984 Canada's Magazine for Electronics & Computing Enthusiasts A Lookat video Cameraslind VCRs Project Bonanza 0.3, Ten short oiler_ lbw Video Distrib Amp Rqpiace boX with a video am *IR Immo. *14 .10101t 71. 10 1 2 - 3 - 2 0 Computer Review: 5 74 3 70924 EXCELTRONIXTORONTO HAMILTON OTTAWA 319 College 72 James St. N. 217 Bank Some prices will go up October, 30th, 1984 1(416)921-8941 1(416)522-4124 1(613)230-9000 Gemini 10X Peripherals 3" Drive for your Apple Apple Compatable to be released soon at an Interface for your Apple unbelievable low price! 1 year warranty e435.00 120 Day Warranty CSA Approved ". 16K RAM Card 554.95 Systems Z80 Card $52.00 Apple //c $1549 5" Monitors Crn 559 Parallel Printer Card $65.00 Apple Macintosh from $3195 (Brand new open frame from Electrohome) RO x 24 Video with soft switch card .$84.00 128K Card - 64K of RAM $117.0010 Meg Hard Disk 128K Card - 128K of RAM $185.00Drive & Controller 51498 KEPCO Heavy Duty EPROM Programmer (with software) .569.00 which plugs right into your machine Switching Power Supply (programs 2716, 2732, 2764) (90 watts max.) Serial Card 579.00 Modem Card $199.00 115V or 220V provision filter and fuse SYSTEM MATE * on board, provides you with +5, PREVENT DOWNTIME, YOTRECIPI°;LIETA + 12, -12, gives you enough power Disk Drives to handle your system plus several for your Apple 5245 LOST DATA, CIRCUIT 585.00 drives with 3.8A on + 12 1 Year Warranty Special price DAMAGE,SERVICING. -

MAXI-BEAM® Sensors Highly Versatile Modularized Photoelectric Sensing Controls
Product Line Specifications MAXI-BEAM® Sensors Highly versatile modularized photoelectric sensing controls • Highly versatile, self-contained, modularized photoelectric sensors; especially suited to industrial environments • Wide selection of rotatable sensor heads, power blocks, and logic timing modules to suit any application • Power blocks for AC or DC operation and for switching of AC or DC loads • Sensor heads include patented AID™ indicator device, which lights a top-mounted LED when the sensor "sees" its own modulated light source and pulses the LED at a rate proportional to the received light signal strength • Status indicator LEDs on power block continuously indicate the state of the output circuit • Models are available in all sensing modes Printed in USA P/N 32883F4A ® MAXI-BEAM MAXI-BEAM™ Sensor Heads Modular Sensors Banner MAXI-BEAM sensors are highly versatile, self-contained, modularized photoelectric sensing controls that are ideally suited to industrial environments. The basic MAXI-BEAM is an ON/OFF switch consisting of three modules: a sensor head, a power block, and a wiring base. The sensor head contains the complete modulated photoelectric ampli- fier as well as the emitter and receiver optoelements. A unique, patented, "programming ring" (supplied with each sensor head) en- All MAXI-BEAM components are encapsulated within rugged, corro- ables you to program your choice of "light" or "dark" operate mode, sion-resistant VALOX® housings which meet or exceed NEMA 1, 3, sensing range, and response time. MAXI-BEAM sensor heads have an 4, 12, and 13 standards. Modules simply snap and bolt together, with easily-accessible multi-turn SENSITIVITY control for precise adjust- no interwiring necessary. -

Iminothioindoxyl As a Molecular Photoswitch with 100€‰Nm Band
ARTICLE https://doi.org/10.1038/s41467-019-10251-8 OPEN Iminothioindoxyl as a molecular photoswitch with 100 nm band separation in the visible range Mark W.H. Hoorens1,2, Miroslav Medved’3,4, Adèle D. Laurent5, Mariangela Di Donato 6,7, Samuele Fanetti 7,8, Laura Slappendel2, Michiel Hilbers 9, Ben L Feringa 2, Wybren Jan Buma 9,10 & Wiktor Szymanski 1,2 Light is an exceptional external stimulus for establishing precise control over the properties 1234567890():,; and functions of chemical and biological systems, which is enabled through the use of molecular photoswitches. Ideal photoswitches are operated with visible light only, show large separation of absorption bands and are functional in various solvents including water, posing an unmet challenge. Here we show a class of fully-visible-light-operated molecular photo- switches, Iminothioindoxyls (ITIs) that meet these requirements. ITIs show a band separation of over 100 nm, isomerize on picosecond time scale and thermally relax on millisecond time scale. Using a combination of advanced spectroscopic and computational techniques, we provide the rationale for the switching behavior of ITIs and the influence of structural modifications and environment, including aqueous solution, on their photochemical proper- ties. This research paves the way for the development of improved photo-controlled systems for a wide variety of applications that require fast responsive functions. 1 Department of Radiology, Medical Imaging Center, University Medical Center Groningen, University of Groningen, Hanzeplein 1, 9713 GZ Groningen, The Netherlands. 2 Faculty of Science and Engineering, Centre for Systems Chemistry, Stratingh Institute for Chemistry, University of Groningen, Nijenborgh 7, 9747 AG Groningen, The Netherlands. -

New Molecular Switch Architectures
SPECIAL FEATURE: SPECIAL FEATURE: PERSPECTIVE PERSPECTIVE New molecular switch architectures Jared D. Harrisa,1, Mark J. Morana,1, and Ivan Aprahamiana,2 Edited by J. Fraser Stoddart, Northwestern University, Evanston, IL, and approved June 13, 2018 (received for review January 22, 2018) In this paper we elaborate on recently developed molecular switch architectures and how these new systems can help with the realization of new functions and advancement of artificial molecular machines. Progress in chemically and photoinduced switches and motors is summarized and contextualized such that the reader may gain an appreciation for the novel tools that have come about in the past decade. Many of these systems offer distinct advantages over commonly employed switches, including improved fidelity, addressability, and robustness. Thus, this paper serves as a jumping-off point for researchers seeking new switching motifs for specific applications, or ones that address the limitations of presently available systems. molecular switches | molecular machines | photochromic compounds Biology has set the stage for what can be accom- decade. The list of systems covered is not meant to be plished with artificial molecular switches and machines exhaustive (7–12). Historically prevalent switches, in- (1, 2), and while molecular machinists take inspiration cluding interlocked molecules, will not be discussed as from it, and aspire to mimic the functions of machines they have been recently reviewed elsewhere (13–18). found in nature, they are also pushing beyond what it Our focus will be on systems that bring unique dimen- can offer. Chemistry, the discipline that “creates its own sions to the field, including interswitch communication object” per 19th-century French chemist Marcellin (19), new molecular motor designs (20–22), and novel Berthelot, lends the toolsets to accomplish this lofty photoswitching capabilities and properties (23–29), goal, as it enables the synthesis of structures limited only among others. -

Field Devices for Process Automation
PROCESS AUTOMATION FIELD DEVICES FOR PROCESS AUTOMATION With regard to the supply of products, the current issue of the following document is applicable: The General Terms of Delivery for Products and Services of the Electrical Industry, published by the Central Association of the "Elektrotechnik und Elektroindustrie (ZVEI) e.V." including the supplementary clause: "Extended reservation of title". We at Pepperl+Fuchs recognise a duty to make a contribution to the future. For this reason, this printed matter is produced on paper bleached without the use of chlorine. THE SUCESS STORY OF PEPPERL+FUCHS 1945 Walter Pepperl and Ludwig Fuchs lay the foundation of Pepperl+Fuchs: The opening of a radio repair shop 1948 Manufacture of transformers 1958 Development and production of the first inductive proximity switch 1973 The first foreign subsidiary is formed in England 1979 Pepperl+Fuchs commences production in Singapore 1988 Michael Fuchs and Claus Michael take over the management of the company and Pepperl+Fuchs becomes a limited liability company 1991 Split into Factory Automation and Process Automation divisions, new product group level control through a company acquisition 1996 The purchase of another company establishes the encoder business 1997 New production facilities open at Veszprem/Hungary 2000 Expansion of the Factory Automation activities with the purchase of Visolux GmbH and the Microswitch and Photoswitch interests from Honeywell; at the same time the Process Automation sector is expanded by the takeover of ELCON 2000 Start of -
Responsive Adhesion and De-Adhesion of Polymers and Nanoparticles
UNIVERSITY OF CALIFORNIA RIVERSIDE Photo- Responsive Adhesion and De-Adhesion of Polymers and Nanoparticles A Dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Bioengineering by Seyed Hossein Mostafavi December 2019 Dissertation Committee: Dr. Christopher J Bardeen, Chairperson Dr. Victor Rodgers Dr. Valentine Vullev Copyright by Seyed Hossein Mostafavi 2019 The Dissertation of Seyed Hossein Mostafavi is approved: Committee Chairperson University of California, Riverside Acknowledgments I would like to first express gratitude to my advisor, Christopher Bardeen, for his tireless support and supervision. He has taught me not only science and systematic approach for solving problems, but I learn how to be kind and giving. There were numerous times that I went to his office hopelessly and broken, come out full of hope and motivated. There were multiple times that I expected he give up on me, he supported me even more. There were times that I felt disappointed and he reached out and gave me a reason to continue my path. Dr Bardeen with any doubts is the greatest scientist I met in my life and for sure one of the kindest one. Chris, thank you for your all your supports that you offered me. It has been an honor to work and learn with you and I will be forever in your debts. I need to thank the love of my life, Shabnam. She was with me during the last 7 years, and endured the hardship of being and living with a grad students. She left her family for me and never stopped supporting me in my course works, research and life. -

ALPHALAS Ultrafast Photodetectors
ALPHALAS GmbH - Ultrafast Photodetectors Product Citations - September 2018 (219 citations) Our customers are from all over the world and include • Industrial Companies: from all branches & from small businesses to largest enterprises • Research Institutions • Academic Institutions • Government Institutions Our products are used by researchers worldwide • from students to top researchers and Nobel prize winners • from universities to top research institutions and laboratories • they are cited in leading research publications, scientific books, dissertations, patents, etc. Below you can find a list of product citations. Most recent citations are listed first. Please note that the list is not exhaustive; citations have been obtained through web search for our company name only. If your publication is missing, please contact us – we will be happy to add it to the list. Product citations for ALPHALAS Ultrafast Photodiodes 1. He, Huan, Xuesheng Liu, Yiheng Song, Congcong Wang, Mingzhen Cao, Anru Yan, and Zhiyong Wang. “LD End-Pumped Nd: YVO4 High Energy High Beam Quality 1064 Nm Picosecond Laser with a Semiconductor Saturable Absorber Mirror.” Optik 175 (December 1, 2018): 172–76. https://doi.org/10.1016/j.ijleo.2018.08.130. 2. Zong, Qing-shuang, Yong Bo, Chuan Guo, Qi Bian, Jin-quan Chang, Wen-jun Li, Li-jiao He, et al. “High Brightness Narrow-Linewidth Microsecond Pulse Green Laser by Frequency Doubling of a Master Oscillator Power Amplifier Nd:YAG Laser.” Optics & Laser Technology 106 (October 2018): 294–98. https://doi.org/10.1016/j.optlastec.2018.04.016. 3. Harries, James R., Hiroshi Iwayama, Susumu Kuma, Masatomi Iizawa, Norihiro Suzuki, Yoshiro Azuma, Ichiro Inoue, et al. -

Ion Channel Photoswitch Reveals Crosstalk Between Intact and Injured Nociceptive Neurons After Nerve Injury
Ion Channel Photoswitch Reveals Crosstalk between Intact and Injured Nociceptive Neurons after Nerve Injury by Christian Herold A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Biophysics in the Graduate Division of the University of California, Berkeley Committee in Charge: Professor Dr. Richard H. Kramer, Chair Professor Dr. Ehud Y. Isacoff Professor Dr. Daniel E. Feldman Professor Dr. Diana M. Bautista Fall 2015 Copyright © by Christian Herold 2015 Abstract Ion Channel Photoswitch Reveals Crosstalk between Intact and Injured Nociceptive Neurons after Nerve Injury by Christian Herold Doctor in Physiology in Biophysics University of California, Berkeley Professor Richard H. Kramer, Chair The development of novel techniques utilizing the advantages of light has created an optical revolution for neuroscience research. Controlling and probing neuronal function with light has provided unprecedented insights by being able to manipulate many neurons simultaneously in intact circuits and living organisms. In my dissertation research, I used novel optical methods to probe the cellular permeability of sensory neuron populations. Primary nociceptive afferents detect, modulate and integrate many pain-related stimuli. Sensory information is transmitted from the periphery through the dorsal root ganglia along labeled lines coding for sensory modalities and receptive fields. Recently, our understanding of sensory processing has been expanded by the discovery of neuronal interactions both on the level of peripheral nerve endings and in the spinal cord. Here I report a crosstalk between injured and intact neuronal population after peripheral nerve injury. This communication is revealed at the somata of sensory neurons distant from the site of injury and correlates with permeability changes of both injured and intact nociceptor populations after injury.