Magnetic Anisotropy of Transition Metal Complexes Nicholas F
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

N Ew Slet T Er
Electron paramagnetic resonance spectroscopy Now located in the PSI, the EPSRC National EPR Research Facility and Service is run by Profs David Collison and Eric McInnes from the School of Chemistry and has been established with £4.1M fund- ing from EPSRC, and £355K from the University of Manchester. The Facility accommodates several Bruker EPR in- struments, allowing c.w. and pulsed EPR measure- ments at frequencies between 1 (L-band) and 95 GHz (W-band), a Quantum Design magnetometer and an ODESSA instrument (built by Dr Nigel Poolton) The EPR Team from right to left: Prof Eric McInnes, Dr Stephen Sproules, Prof David Collison, Dr Floriana Tuna, that combines optically detected magnetic resonance Dr Brian Tolson, Miss Chloe Stott, Dr Nigel Poolton (absent) (ODMR) with photo-EPR (both 34 GHz; 0-4 T mag- Facilities: Frequency (GHz): 1, 4, 9.5, 24, 34, 94 net). Together these make a unique research base for Frequency Band: L-, S-, X-, K-, Q-, W- studying various types of paramagnetic species and Modes: Parallel and perpendicular at X-band materials. Temperature Range: 4.2 to 300 K all bands, to 500 K at X-band only Researchers across the country are using the Facility on a regular basis. PhD students and academics are For further details see the Facility website: encouraged to visit the Centre and to gain ―hands on‖ http://www.epr.chemistry.manchester.ac.uk/ experience. Newsletter Winter 2011/12 This newsletter consists of a combination of articles, highlighting both recent grant successes and those of a personal nature. Until further notice, items for future newsletters and/or the PSI website should be sent to [email protected]. -

James Walsh Postdoctoral Fellow Department of Chemistry
James Walsh Postdoctoral Fellow Department of Chemistry Northwestern University Evanston, IL 60208 phone: (847) 491-4356 email: [email protected] Current Position Assistant Professor, Department of Chemistry, University of Massachusetts Amherst (Sep 2019) Postdoctoral Fellow, Department of Chemistry, Northwestern University (2015 – Present) Advisors: Prof. Danna Freedman and Prof. Steven Jacobsen Background Postdoctoral Fellow, Aarhus University (2015) Advisor: Dr. Jacob Overgaard Ph.D. in Inorganic Chemistry, University of Manchester (2010 – 2014) Advisors: Prof. David Collison, Prof. Eric McInnes, Prof. Richard Winpenny Master’s in Chemistry, University of Manchester (2006 – 2010) Honors International Institute for Nanotechnology Outstanding Researcher Award (2017) Activities and Interests My research interests center on the use of extremely high pressure for the synthesis of completely new structures and chemical bonds. More broadly, I am interested in the use of X-ray crystallography as a tool to examine reaction mechanism in solid-state chemistry. I am a frequent user of the HPCAT and GSECARS beamlines at the APS. I collaborate closely with beamline scientists across both sectors and have averaged 8 shifts each run over the last four years. The APS is a world leader in the field of high pressure and is the source of many of the cutting-edge techniques that have since been adopted by other beamlines. This trend of origination is set to continue with the upgrade, which will position the APS at the forefront of synchrotron radiation science. The enormous increase in flux will make it the flagship of a new generation of experiments that allow for crystallographic access to unprecedented ultrafast timescales. -

Electron Spin Resonance
The EPSRC National EPR/ENDOR Service is based across the Universities of Manchester, St Andrews and Cardiff. Manchester (Chemistry Department) provides facilities for CW EPR at L (ca. 1), S (4), X (9), K (24) and Q-bands (34 GHz) at ELECTRON SPIN temperatures between 4 and 300 K at all frequencies, and up to 700 K at X-band. X- and Q-band CW ENDOR facilities are available at Cardiff. St Andrews (Physics and RESONANCE RRSSxxCC Astronomy Department) offer CW EPR at 90, 180 and 270 GHz. The Service is available ROYAL SOCIETY OF CHEMISTRY to all academic researchers eligible for EPSRC funding, and is free at "point of sale". GROUP Workers in the areas of biological, pharmaceutical or materials science are welcomed. Research collaborations with international, industrial or institutional organisations are possible. Anyone interested in using the Service should contact: Dr David Collison Newsletter ([email protected]) or Dr Eric McInnes ([email protected]), Dr Graham March 2003 Smith (St Andrews, [email protected]), or Dr Damien Murphy (Cardiff, [email protected]) in the first instance. Eric McInnes ESR GROUP COMMITTEE. SpinDrift from John Walton (83 papers) with applications to protein Dr Mark E. Newton, Department of In its early years ESR spectroscopy was dynamics, membrane-peptide The ESR Group committee was elected at Chemistry, University of Warwick Dr Graham Smith, School of Physics, one of the key reference points for testing interactions, muscle fibers and the AGM held in Aberdeen on 10th April QM theory. The classic INDO semi- carbohydrates. -
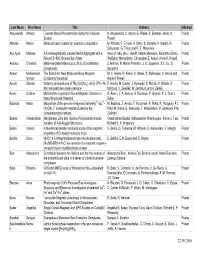
Last Name First Name Títle Authors Abstract Abouelwafa Ahmed Towards Novel Photoswitches Using the Viologen A
Last Name First Name Títle Authors Abstract Abouelwafa Ahmed Towards Novel Photoswitches Using the Viologen A. Abouelwafa, C. Anson, B. Pilawa, S. Balaban, Annie. K. Poster System Powell Affronte Marco Molecular spin clusters for quantum computation M. Affronte, F. Troiani, A. Ghirri, S. Carretta, P. Santini, R. Poster Schuecker, G. Timco and R. E. Winpenny Ako Ayuk Manase A Ferromagnetically coupled Mn19 Aggregate with a Ayuk M. Ako, Ian J. Hewitt, Valeriu Mereacre, Rodolphe Clérac, Poster Record S=83/2 Ground Spin State Wolfgang Wernsdorfer, Christopher E. Anson, Annie K. Powell Ambrus Christina Metal-templated Macrocyclic (N3O2) Coordination C.Ambrus, B. Møller Petersen, J. O. Jeppesen, S.X. Liu, S. Poster Compounds Decurtins Anwar Muhammad The Search for New Molecular Base Magnets M. U. Anwar, R. Kania, G. Abbas, S. Mukherjee, C. Anson and Poster Usman Containing Vanadium Annie K Powell Arnold Zdenek Ordering temperatures of TM3[Cr(CN)6]2.nH2O (TM – Ni, Z. Arnold, M. Cieslar, J. Kamarád, S. Maťaš, M. Mihalik, Z. Poster Mn) nanoparticles under pressure Mitróová, V. Zeleňák, M. Zentková, and A. Zentko Aromí Guillem Multidentate Ligands for Novel Magnetic Clusters or G. Aromí, L. A. Barrios, O. Roubeau, P. Gamez, S. J. Teat, J. Poster Nano-Structured Materials Ribas 5+ 2+ Balanda Maria Magnetism of the genuine bi-layered (tetrenH5) -Cu - M. Bałanda, Z. Arnold, T. Korzeniak, R. Pełka, R. Podgajny, F.L. Poster 3- [W(CN)8] molecular magnet studied by the Pratt, M. Rams, B. Sieklucka, T. Wasiutyński, M. Zentkova, P.M. complementary methods Zieliński Baskar Viswanathan Manganese, Zinc and Sodium Polyoxoantimonates: Viswanathan Baskar, Maheswaran Shanmugam, Simon J. -

Esr Conf 2019.Pdf
Progress in Rapid Scan 256 scans 1048576 scans 27.2 SNR 1687.6 SNR 12 msec averaging time 51 sec averaging time Recovering Small Signals by Clean and Efficient Averaging Rapid Scan of E’ center in quartz measured with 20.5 kHz scan rate Clean white noise S/N scales with √(# averages) A million scans in 50 sec in real-time Discover more at: www.bruker.com/epr EPR Innovation with Integrity rapid-scan-ad.indd 1 11/19/2018 8:18:35 AM WELCOME On behalf of the ESR Spectroscopy Group of the Royal Society of Chemistry, welcome to the 52nd Annual International Meeting of the Group held at the Golden Jubilee Conference Hotel in Clydebank, Glasgow. The scientific sessions are headlined by our plenary and keynote speakers, as well as the recipient of the 34th Bruker Prize, Marina Bennati, and 5th Bruker Thesis Prize, Claire Motion. For younger researchers, the 22nd Annual JEOL Prize competition will run on Monday afternoon, and there are prizes for the Flash Talks on Wednesday and poster presentations. We are especially grateful to the support provided by our generous sponsors of the meeting. I hope you will have an interesting, challenging and informative time whilst in Glasgow. Stephen Sproules, Local Organizer Plenary Speakers Elena Bagryanskaya Marilena Di Valentin Russian Academy of Sciences Novosibirsk, Russia University of Padova, Italy Etienne Goovaerts David Norman University of Antwerp, Belgium University of Dundee, UK Keynote Speakers Alice Bowen Nicholas Chilton University of Oxford, UK The University of Manchester, UK Richard Cogdell -

EPR @ Warwick 14
The 46th Annual International Meeting of the ESR Spectroscopy Group of the Royal Society of Chemistry The University of Warwick 7th – 11th April 2013 Contents Conference Programme 1 Information for delegates 6 Getting there and How to find 6 The University of Warwick campus map 8 Speaker/poster presenter information 9 Checking in/out 9 Internet access 9 Car parking/taxis 10 Accompanying persons 11 Free afternoon 11 Conference sponsors 13 EPR @ Warwick 14 Bruker prize lecture and reception 15 JEOL student prize lectures 16 Committee of the ESR spectroscopy Group of the RSC 17 List of participants 18-22 Next meeting (2014) 23 Abstracts for Talks Abstracts for Posters The 46th International Meeting of the ESR Spectroscopy Group, Warwick 2013 The 46th International Meeting of the ESR Spectroscopy Group, Warwick 2013 Conference Programme: The 46th Annual International Meeting of the ESR Spectroscopy Group, 7th – 11th April 2013 Sunday 7th April 16.00 – 18.00 Registration Conference Reception (Collection of Room Keys) 18.30 – 20.00 Dinner Rootes Restaurant 20.00 – 22.30 RSC Reception The Bar/Bar Fusion, Rootes Building Monday 8th April 07.30 – 08.55 Breakfast Rootes Restaurant Session 1 Chair: Gavin Morley Physics Lecture Theatre 08.55 – 09.00 Mark Newton Welcome and Conference Opening 09.00 – 09.40 K1 Joerg Wrachtrup Keynote Lecture: Sensing nuclear spins at the nanoscale Tuning Molecular Magnets for Quantum Information 09.40 – 10.00 O1 Amy Webber Processing 10.00 – 10.20 O2 Floriana Tuna Single Molecule Magnetism in f-Block Metal Complexes -

James P. S. Walsh
James P. S. Walsh [email protected] University of Massachusetts Amherst Department of Chemistry +1 (413) 545–1557 Physical Sciences Building http://jpswalsh.com 690 N Pleasant St [email protected] Amherst, MA 01003 RESEARCH POSITIONS Assistant Professor Sep 2019 – Present University of Massachusetts Amherst, United States Postdoctoral Fellow with Prof Danna Freedman May 2015 – Aug 2019 Northwestern University, United States Postdoctoral Fellow with Dr Jacob Overgaard Mar 2015 – May 2015 Aarhus University, Denmark Research Associate with Dr Alistair Fielding Nov 2014 – Feb 2015 University of Manchester, United Kingdom EDUCATION PhD in Inorganic Chemistry Sep 2010 – Oct 2014 Nanoscience Doctoral Training Centre, University of Manchester, United Kingdom Advisors: Prof David Collison, Prof Eric McInnes, and Prof Richard Winpenny MChem in Chemistry with Forensic Science Sep 2006 – Aug 2010 University of Manchester, United Kingdom HONOURS AND AWARDS COMPRES Postdoc Travel Scholarship (Annual Meeting, Santa Ana Pueblo, New Mexico, USA) Aug 2018 IUCr-HP Early Career Travel Award (IUCr Commission on High-Pressure, Honolulu, Hawaiʻi, USA) Jul 2018 Northwestern Postdoctoral Professional Development Travel Award Dec 2017 International Institute for Nanotechnology Outstanding Researcher Award Sep 2017 COMPRES Postdoc Travel Scholarship (Annual Meeting, Santa Ana Pueblo, New Mexico, USA) Jul 2017 Marie Skłodowska-Curie Masterclass Invited Participant (Aarhus University, Denmark) May 2016 INVITED TALKS Special Seminar (Georgia Institute of Technology, -

The 44Th Annual International Meeting
The 46th Annual International Meeting of the ESR Spectroscopy Group of the Royal Society of Chemistry The University of Warwick 7th – 11th April 2013 Contents Conference Programme 1 Information for delegates 6 Getting there and How to find 6 The University of Warwick campus map 8 Speaker/poster presenter information 9 Checking in/out 9 Internet access 9 Car parking/taxis 10 Accompanying persons 11 Free afternoon 11 Conference sponsors 13 EPR @ Warwick 14 Bruker prize lecture and reception 15 JEOL student prize lectures 16 Committee of the ESR spectroscopy Group of the RSC 17 List of participants 18-22 Next meeting (2014) 23 Abstracts for Talks Abstracts for Posters The 46th International Meeting of the ESR Spectroscopy Group, Warwick 2013 The 46th International Meeting of the ESR Spectroscopy Group, Warwick 2013 Conference Programme: The 46th Annual International Meeting of the ESR Spectroscopy Group, 7th – 11th April 2013 Sunday 7th April 16.00 – 18.00 Registration Conference Reception (Collection of Room Keys) 18.30 – 20.00 Dinner Rootes Restaurant 20.00 – 22.30 RSC Reception The Bar/Bar Fusion, Rootes Building Monday 8th April 07.30 – 08.55 Breakfast Rootes Restaurant Session 1 Chair: Gavin Morley Physics Lecture Theatre 08.55 – 09.00 Mark Newton Welcome and Conference Opening 09.00 – 09.40 K1 Joerg Wrachtrup Keynote Lecture: Sensing nuclear spins at the nanoscale Tuning Molecular Magnets for Quantum Information 09.40 – 10.00 O1 Amy Webber Processing 10.00 – 10.20 O2 Floriana Tuna Single Molecule Magnetism in f-Block Metal Complexes -

High-Frequency and High-Field EPR/ESR in Tallahassee, FL
2012 epr volume 22 number 2 news A letter zz R PELDOR PELDOR signals The Publication of the International time (ns) EPR (ESR) Society newsepr letter www.epr-newsletter.ethz.ch Officers of the international ePr (esr) society The official publication of the International EPR (ESR) Society is supported by the Society, by corporate and President secretArY other donors, the Zavoisky Physical-Technical Institute of the Russian Academy of Sciences, Kazan, Russian seigo Yamauchi sushil K. Misra Federation, and the Swiss Federal Institute of Technology, Institute of Multidisciplinary Research for Concordia University, Zürich, Switzerland. Advanced Materials (IMRAM), 1455 de Maisonneuve Boulevard West, Tohoku University, Montreal (Quebec), H3G 1M8, Canada Katahira-2-1-1, phone: 514-848-2424 ext. 3278, fax: 514-848-2828 editOr Aobaku, Sendai 980-8577, Japan e-mail: [email protected] Laila V. Mosina phone: 81-22-217-5617, fax: 81-22-217-5616 web: physics.concordia.ca/faculty/misra.php Zavoisky Physical-Technical Institute e-mail: [email protected] Russian Academy of Sciences treAsurer Kazan, Russian Federation Vice Presidents tatyana i. smirnova [email protected] Americas North Carolina State University, AssOciAte editOrs Lawrence Berliner Department of Chemistry, Candice S. Klug Department of Chemistry and Biochemistry, Campus Box 8204, Raleigh, NC 27695-8204, USA Medical College of Wisconsin University of Denver, phone: (919) 513-4375, fax: (919) 513-7353 Milwaukee, WI, USA 2090 E. Iliff Ave, Denver, CO, OR 80208 USA e-mail: [email protected] [email protected] phone: 303-871-7476, fax: 303-871-2254 Hitoshi Ohta e-mail: [email protected] ImmediAte PAst President Molecular Photoscience Research Center, web: www.du.edu/chemistry/Faculty/lberliner.html Jack H. -

Electron Spin Resonance RS C
News from the UK cwEPR National Service at Manchester The cwEPR National Service is now located on a single site, and as well as the unique range of microwave frequencies (L, S, X, K and Q-bands), the W-band (94 GHz) spectrometer has been installed and is proving to be sensitive, responsive and relatively robust. The magnetic field is supplied by a 6 T Oxford horizontal magnet, allowing wide field sweeps routinely. Resolution of very small g-value anisotropies, measurement of tiny samples, determination of large zero-field splittings and power saturation studies (even at room temperature) will ELECTRON SPIN extend the range of experiments for users of the Service. Recent developments with the microwave frequencies RESONANCE RSxC include routine in situ electrochemical generation and also optical excitation. Interpretation by spectrum RSxC simulation of data collected in users’ own laboratories is also provided in some cases. Recently, pilot studies in GROUP ROYAL SOCIETY OF CHEMISTRY collaboration with the EPSRC National Service for Computational Chemistry Software have been initiated, whereby in the future a project being studied by one Service could have access to the other. It is hoped to implement this inter-Service arrangement if both Services are renewed this year, and subject to the approval of EPSRC. EPR spectra at higher frequencies (180/270 GHz) remain available through collaborations with St Newsletter Andrews (Dr Graham Smith), as do ENDOR measurements (X and Q-bands) with Cardiff (Dr Damien Murphy). April 2005 The process for the renewal of the cwEPR National Service from March 2006 is underway, although the provision of pulse spectroscopy is specifically excluded in the call made by EPSRC. -

ESR2008 Conference Book
The 41st Annual International Meeting of the Electron Spin Resonance Group of the Royal Society of Chemistry “AdvancedTechniques and Applications of EPR ” S H N N H N N Cu S O H N University College London 6th – 10 th April 2008 Contents Conference Programme 3 General Information for Delegates 7 Maps of University College London 9 Committee of the ESR Spectroscopy Group of the RSC 11 Local Organisation – Acknowledgements 12 JEOL Student Prize Lectures and Reception 13 Bruker Lecture and Reception 14 ESR at UCL – A brief history 15 Obituary – Mike Evans 17 Next Meeting – Norwich 2009 22 Abstracts for Talks 23 Abstracts for Posters 67 Title Index 115 Author Index 119 List of Participants 121 2 Conference Programme SUNDAY 6th April CONFERENCE OPENING, REGISTRATION, “EVENs” POSTER 19:30 – 23:00 SESSION & RECEPTION South Cloisters sponsored by the ESR Spectroscopy Group of the RSC MONDAY 7th April Session Chair: David Collison 08:50 – 09:00 Richard Catlow, FRS Welcome note Keynote Lecture: Exploring Spin Chemistry in Melanin and 09:00 – 09:45 Jim Norris Retinal Pigment Epithelial Eye Cells Using Time-Resolved EPR and Static Magnetic Fields Evidence for Direct UVA- and Solar radiation-induced 09:55 – 10.10 Rachel Haywood Protein, Lipid and DNA oxidation Relevant to Human Skin Photodamage 10:15 – 10:30 Gert Denninger ESR on radicals trapped in tartrates from red wine 10:35 – 11:05 Tea & Coffee South Cloisters Session Chair: Alwyn Davies, FRS Invited Lecture: Discrimination of geometrical epoxide 11:05 - 11:25 Damien Murphy isomers by ENDOR spectroscopy -

Electron Spin Resonance RS?C
Development of the UK EPR National Service at Manchester The EPR National Service provides high quality EPR facilities and expertise for members of the UK academic community. Funded through the EPSRC Chemistry Programme, the service has a unique range of EPR instrumentation and will now be developed to include a commercial high field ELECTRON SPIN W-band instrument. The service is also being restructured to locate all the instrumentation at a RESONANCE RRSSxxCC single centre at Manchester having an equipment base allowing 6 microwave frequencies (L, S, X, K, Q and W-bands), with options for variable temperature, single crystal, electrochemical studies, ROYAL SOCIETY OF CHEMISTRY and spectrum simulation. During the one-year transitional phase there will also be a continuation of GROUP the high field service element at St-Andrews (90/180/270 GHz). Access to ENDOR measurements can be made via collaborative arrangements at Cardiff. Training and extending the user base are important elements of the service and the centre Newsletter encourages suppliers of samples to visit the centre in order to gain hands on experience in EPR. March 2004 General information on the EPR Service can be found at the service web site: http://mch3w.ch.man.ac.uk/services/epresr/EPRmain.htm. Contact Carmine Ruggiero at [email protected] for information about other EPSRC services. David Collison SpinDrift from John Walton These two techniques were then ESR GROUP COMMITTEE. Dr Mark E. Newton, Department of More than 4000 papers on ESR and its elegantly combined to produce site Chemistry, University of Warwick sibling techniques appeared in the last 15 directed spin labelling.