DOCSLIB.ORG

AP Statistics Semester I Final Exam Review

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
AP Statistics Semester I Final Exam Review AP Statistics Semester I Final Exam Review 1. Jerry and George are playing golf. Their scores on the first 9 holes are shown in the table below. For each player, find the mean, median and mode score. Use your results to explain which measure of central tendency gives the best comparison of the abilities of the two players. Player/Hole 1 2 3 4 5 6 7 8 9 Total Mean Median Mode Jerry 4 7 5 2 4 7 3 6 7 45 George 3 5 4 2 3 7 3 5 16 48 2. The histograms below represent the distributions of the batting averages of the top National League and American League batters for the years shown. Examine the histograms and write a one paragraph observation about the data. Be sure to discuss such measures of center and spread. Also, compare the three distributions, noting any apparent trends. 3. Below are the winning men’s long jump distances for the first 22 Olympic Games. Year Winner Meters Year Winner Meters 1896 Ellery Clark 6.35 1952 Jerome Biffle 7.57 1900 Alvin Kraenzlin 7.18 1956 Gregory Bell 7.83 1904 Myer Prinstein 7.34 1960 Ralph Boston 8.12 1908 Francis Irons 7.48 1964 Lynn Davies 8.07 1912 Albert Gutterson 7.60 1968 Robert Beamon 8.90 1920 William Pettersson 7.15 1972 Randy Williams 8.24 1924 De Hart Hubbard 7.44 1976 Arnie Robinson 8.35 1928 Edward Hamm 7.73 1980 Lutz Dombrowski 8.54 1932 Edward Gordon 7.63 1984 Carl Lewis 8.54 1936 Jesse Owens 8.06 1988 Carl Lewis 8.72 1948 William Steele 7.82 1992 Carl Lewis 8.67 a) Create a stem-and-leaf plot of the data. Be sure to add a legend or key. b) Now plot the same data with a time plot from 1896 to 1992. Label appropriately. c) Write a one-paragraph conclusion about these plots. Compare/contrast the two plots, noting any advantages one plot has over the other toward analyzing the data. 4. The scores of the winning teams in the Rose Bowl games played from 1931 to 1980 are arranged in ascending order in the list below. 7 7 7 7 9 10 10 13 13 14 14 14 14 14 14 17 17 17 17 17 17 18 20 20 20 21 21 21 21 23 24 25 27 27 27 28 29 29 34 34 35 35 38 40 42 42 42 44 45 49 a) Create a histogram of the data, with bars of width 5 (1-5, 6-10, 11-15, 16-20, etc...). b) Find the 5-number summary of the data and use it to construct a box plot. MIN Q1 MEDIAN Q3 MAX c) Describe the shape of the data from the histogram. Explain how it is usually possible to know the shape of the histogram simply by looking at the box plot. d) Is the highest value in this data an outlier? Use a formula to justify your response 5. Read the problem description below left: a) Which curve do you think shows the weights of newly minted quarters, which curve the coins after five years, and which curve the coins after ten years? b) What happens to the average weight of the coins as time passes? c) What happens to the standard deviation of the weight of the coins as time passes? 6. Lengths of pregnancy of women having children are normally distributed, with a mean of 266 days and a standard deviation of 16 days. a) Sketch a normal curve from this information, labeling the mean and 3 standard deviations in both directions. Use your sketch to answer questions b-d b) What percentage of pregnancies last between 250 and 282 days? __________ c) What percentage of pregnancies last between 250 and 298 days? __________ d) What percentage of pregnancies last between 234 and 266 days? __________ e) A letter once appeared in Dear Abby’s newspaper column from a woman who said she had been pregnant for 310 days before giving birth to her baby. This is considerably longer than the typical pregnancy. What percentage of pregnancies last 310 or more days? Show a sketch and all necessary work. 7. Consider the following data, which give the weight (in thousands of pounds) x and gasoline mileage (miles per gallon) y for ten different automobiles. x 2.5 3.0 4.0 3.5 2.7 4.5 3.8 2.9 5.0 2.2 y 40 43 30 35 42 19 32 39 15 14 a) Use your calculator to find the least-squares regression equation, r and r2 for this data. Also use your calculator to make a scatter plot of the data. Reg. Eq.: ___________________________________ r: _____________ b) Using your results from part (a), describe the strength of the linear relationship between these two variables. c) Use the results from part (a) to complete the table below (round to nearest tenth). Weight (x) Actual MPG ( y ) Predicted MPG ( y ) Residual 3.0 43 4.0 30 5.0 15 d) Use your calculator to create a residual plot.. e) What does this residual plot tell us? Explain in a few sentences. 8. Answer TRUE if the statement is always true. If the statement is not always true, replace the word(s) in bold with words that make the statement always true. a) Correlation analysis is a method of obtaining the equation that represents the relationship between two variables. b) The linear correlation coefficient is used to determine the equation that represents the relationship between two variables. c) A correlation coefficient of zero means that the two variables are perfectly correlated. d) Whenever the slope of the regression line is zero, the correlation coefficient will also be zero. e) When r is positive, the slope will always be negative. f) The slope of the regression line represents the amount of change expected to take place in y when x increases by one unit. g) The calculated value of r2 represents the fraction of variation in the y variable which can be explained by the linear model. h) Correlation coefficients range between 0 and 1. i) The y variable is called the explanatory variable. j) The line of best fit is used to predict the average value of y that can be expected to occur for a given value of x. k) If a point has a residual of zero, then it lies on the line of best fit. l) If a point has a negative residual, then it lies above the line of best fit. 9. An issue of the school newspaper at a university reported the results of a survey conducted by the office of student development on the percent of students who use their student government representative to convey their feelings on university issues. a) What is the population of interest in this survey? b) In addition to recording whether the respondent uses the representative, what other variables do you think should be measured? c) Explain in some detail how you would take a sample for this survey. Identify the sampling method used in the following: d) Personal interviews of students leaving the cafeteria after lunch. e) Sending a survey to the first name on each page of the student directory. f) Asking students to respond to a survey in an issue of the school newspaper. 10. A clothing manufacturer would like to compare the durability of a newly designed line of children’s clothes with that of its existing line of clothing. To do so, the company will conduct an experiment using sets of identical twins. One of each set of twins will wear the old clothing and the other one will wear the new clothing. The children will then be allowed to play for a period of time, after which the clothing will be evaluated for durability. a) Why is this an experiment? b) What type of experiment is this? c) Describe in detail how you would utilize the 3 Principles of Experimental Design to ensure that the results of this experiment are trustworthy. • CONTROL • RANDOMIZATION • REPLICATION 11. You roll two 6-sided dice. The first die has 2 1’s, 2 2’s and 2 3’s on it. The other has 3 2’s and 3 3’s. You will roll these dice and find the sum. a) Show all possible outcomes for these two dice when rolled together. b) Make a probability distribution table for the sum of these two dice c) What is the probability that the sum is odd? d) What is the probability that the sum is a multiple of 3? e) What is the mean value of this discrete random variable? 12. A bag contains 5 marbles (3 are red and 2 are blue). You draw a marble out of the bag at random and replace it. Let X = the number of marbles drawn until you get a red marble. a) Explain why X has a Geometric Distribution. Find the probability that... b) It takes 4 draws to get the first red marble. c) It takes 4 or fewer draws to get the first red marble. d) It takes more than 3 draws to get the first red marble. e) On average, how many draws would we expect to make to get the first red? 13. A new television show has a 20% chance of being successful. Assume that NBC will introduce eight new shows this spring. Let X = the number of those shows that will succeed.
Load more

Recommended publications
  • Sports Council Wales Annual Report 2004-05
    Developing Sport & Physical Activity in Wales The Sports Council for Wales is the national organisation responsible for developing and promoting sport and active lifestyles. It is the main adviser on sporting matters to the Welsh Assembly Government and is responsible for distributing funds from the National Lottery to sport in Wales. The Council aims to be one of the main Subsequently, the Council’s main focus is to contributors to ‘Climbing Higher’, the Welsh increase the frequency of participation by Assembly Government’s strategy for sport persuading those who are currently and physical activity. It fully subscribes to sedentary to become more active and to the Assembly’s vision for a physically active encourage people, young and old, to and sporting nation, namely: develop a portfolio of activities through which to achieve healthy levels of activity. • Wales needs to be more physically active The themes of the Council’s work are: in order to be a healthier nation; • Active young people; • Wales needs healthy citizens to deliver long term prosperity; • Active communities; • Wales needs to maximise the synergy • Developing people; between sport, active recreation and the • Developing places; natural environment; • Developing performance and excellence. • Wales needs people to be more physically literate; In addition, the Council has committed to a shift from grants management to positioning • Wales needs more physically active itself as a development agency by becoming communities; an effective advocate for sport and physical • Wales needs systematic and sustainable activity, the marketing of healthy lifestyles success in the sports that matter most and intervention directed at the best use of to us.
    [Show full text]
  • Deutsche Olympiasieger, Welt- Und Europameister (1896 - 2019)
    Deutsche Olympiasieger, Welt- und Europameister (1896 - 2019) Summe 1896 bis 2019: 72 Olympiasiege 60 Weltmeistertitel 183 Europameistertitel vor 1945: 6 Olympiasiege 19 Europameistertitel 1949 - 1990: DLV: 14 Olympiasiege 3 Weltmeistertitel 35 Europameistertitel DVfL: 40 Olympiasiege 21 Weltmeistertitel 91 Europameistertitel 1991 - 2019: 12 Olympiasiege 38 Weltmeistertitel 44 Europameistertitel 1972 100m Hürd. Annelie Ehrhardt O l y m p i a s i e g e r 1972 4x100 m Krause, Mickler, Richter, Rosendahl 1928 800 m Lina Radke 1972 4x400 m Käsling, Kühne, Seidler, Zehrt 1936 Kugel Hans Woellke 1972 Hochsprung Ulrike Meyfarth 1936 Hammer Karl Hein 1972 Weitsprung Heide Rosendahl 1936 Speer Gerhard Stöck 1972 Speer Ruth Fuchs 1936 Diskus Gisela Mauermayer 1936 Speer Tilly Fleischer 1976 Marathon Waldemar Cierpinski 1976 Kugel Udo Beyer 1960 100 m Armin Hary 1976 100 m Annegret Richter 1960 4x100 m Cullmann, Hary, 1976 200 m Bärbel Wöckel Mahlendorf, Lauer 1976 100m Hürd. Johanna Schaller 1976 4x100 m Oelsner, Stecher, 1964 Zehnkampf Willi Holdorf Bodendorf, Wöckel 1964 80m Hürden Karin Balzer 1976 4x400 m Maletzki, Rohde, Streidt, Brehmer 1968 50km Gehen Christoph Höhne 1976 Hochsprung Rosemarie Ackermann 1968 Kugel Margitta Gummel 1976 Weitsprung Angela Voigt 1968 Fünfkampf Ingrid Mickler 1976 Diskus Evelin Jahl 1976 Speer Ruth Fuchs 1972 20km Gehen Peter Frenkel 1976 Fünfkampf Sigrun Siegl 1972 50km Gehen Bernd Kannenberg 1972 Stabhoch Wolfgang Nordwig 1980 Marathon Waldemar Cierpinski 1972 Speer Klaus Wolfermann 1980 50km Gehen Hartwig Gauder
    [Show full text]
  • California Golden Bears 2021 Track & Field Record Book 1
    CALIFORNIA GOLDEN BEARS 2021 TRACK & FIELD RECORD BOOK 1 2021 CALIFORNIA TRACK & FIELD 2021 SCHEDULE QUICK FACTS Date Day Meet Site Name ............... University of California January Location ....................... Berkeley, Calif. 22-23 Fri.-Sat. at Air Force Invitational Colorado Springs, Colo. Founded ...................................... 1868 February Enrollment ................................ 40,173 19 Fri. at Air Force Collegiate Open Colorado Springs, Colo. Nickname ...................... Golden Bears 25-27 Thu.-Sat. at Championships at the Peak Colorado Springs, Colo. Colors ............ Blue (282) & Gold (123) Chancellor ........................ Carol Christ March Director of Athletics ... ....Jim Knowlton 6 Sat. California Outdoor Opener Berkeley, Calif. Home Facility ........... Edwards Stadium 11-13 Fri.-Sat. at NCAA Indoor Championships Fayetteville, Ark. (22,000) 20 Sat. at USC Dual Los Angeles, Calif. 2020 Men’s Finishes (indoor): 26-27 Fri.-Sat. at Aztec Invitational San Diego, Calif. MPSF/NCAA ........................N/A/N/A 2020 Men’s Finishes (outdoor): April Pac-12/NCAA ......................N/A/N/A 3 Sat. at Stanford Invitational Stanford, Calif. 2020 Women’s Finishes (indoor): 10 Sat. USC Dual Berkeley, Calif. MPSF/NCAA ........................N/A/N/A 2020 Women’s Finishes (outdoor): May Pac-12/NCAA ......................N/A/N/A 1 Sat. Big Meet Berkeley, Calif. 14-16 Fri.-Sun. at Pac-12 Outdoor Championships Los Angeles, Calif. ATHLETIC COMMUNICATIONS 27-29 Thu.-Sat. at NCAA West Preliminary Rounds College Station,
    [Show full text]
  • 2Oo6 NON-GRADUATES Fa Edward Lester Klink, 1907
    2oo6 NON-GRADUATES f.a. Edward Lester Klink, 1907--9, Syracuse, N. Y. f .a. EvA ANNA KLINK, 1906-, Syracuse, N. Y. f.a. Irene Huldath Klink, 1906-8, Syracuse, N. Y. f.a. EDNA MARKELL KLOCK, 1908-, St. Johnsville, N. Y. l.a. Edwin Judson Klock, 1884-5, <I> K 'Y (at Syracuse), A 1, (at Middle­ bury, B.S. (Middlebury) 1888. A.M. (same), 1891. Married 13 Jan., 1891, Minnie L. Stafford of Washington, Vt. Clergyman, Con­ gregational, Norwich, N.Y. f.a. Frank B. Klock, 1884-5, Syracuse, N. Y. l.a. Grace Klock, 1889--90, f' <I> B1 Oneida, N. Y. l.a. *Harry Sanford Klock, 1884--6, A K E, Oneida, N. Y. Died 19 May, 1896, at Kansas City, Mo. a.s. KARL THEODORE KLocK, 1907-, Syracuse, N. Y. f.a. Nellie Louisa Klock (Nye), 1884-5, Syracuse, N. Y. Married 6 June, 1888, Francis H. Nye, Jr., of Syracuse. Residence, Syracuse, N.Y. t. Julia M. Klube, 1907-8, Syracu>e, N. Y. f.a. KATHARINE MAY KLuMP, 1907-, Watertown,_N. Y. l~a. Alice A. Knapp, (Kellogg), 1873-4, A <1>, S. Spafford, N. Y. l.a. ALICE L. KNAPP, 1909-, Geneva, N.Y. Daughter of No. 431. f.a. Elizabeth H. Knapp, 1874-5, Binghamton, N.Y. t. Ella Maria Knapp, 1906-8, Dundee, N. Y. f.a. Florence E. S. Knapp, 1903-7, Camillus, N. Y. a.s. Howard Edward Knapp, Jamestown, N.Y. f.a. Leona May Knapp, 1907--9, Camden, N. Y. I.a. Matthew H. Knapp, 1905--6, Syracuse, N.
    [Show full text]
  • All Time Men's World Ranking Leader
    All Time Men’s World Ranking Leader EVER WONDER WHO the overall best performers have been in our authoritative World Rankings for men, which began with the 1947 season? Stats Editor Jim Rorick has pulled together all kinds of numbers for you, scoring the annual Top 10s on a 10-9-8-7-6-5-4-3-2-1 basis. First, in a by-event compilation, you’ll find the leaders in the categories of Most Points, Most Rankings, Most No. 1s and The Top U.S. Scorers (in the World Rankings, not the U.S. Rankings). Following that are the stats on an all-events basis. All the data is as of the end of the 2019 season, including a significant number of recastings based on the many retests that were carried out on old samples and resulted in doping positives. (as of April 13, 2020) Event-By-Event Tabulations 100 METERS Most Points 1. Carl Lewis 123; 2. Asafa Powell 98; 3. Linford Christie 93; 4. Justin Gatlin 90; 5. Usain Bolt 85; 6. Maurice Greene 69; 7. Dennis Mitchell 65; 8. Frank Fredericks 61; 9. Calvin Smith 58; 10. Valeriy Borzov 57. Most Rankings 1. Lewis 16; 2. Powell 13; 3. Christie 12; 4. tie, Fredericks, Gatlin, Mitchell & Smith 10. Consecutive—Lewis 15. Most No. 1s 1. Lewis 6; 2. tie, Bolt & Greene 5; 4. Gatlin 4; 5. tie, Bob Hayes & Bobby Morrow 3. Consecutive—Greene & Lewis 5. 200 METERS Most Points 1. Frank Fredericks 105; 2. Usain Bolt 103; 3. Pietro Mennea 87; 4. Michael Johnson 81; 5.
    [Show full text]
  • Welsh Athletics Milestones
    Welsh Athletics Milestones Recalled by Clive Williams 1860 John Chambers holds a sports meeting at Hafod House, Aberystwyth - probably the first record of an athletics meeting being held in Wales 1865 Chambers organises “athletic sports” at Aberystwyth. 1865 William Richards, born in “Glamorgan” sets a world record for the mile with 4 mins. 17 ¼ seconds. 1871 St. David’s College Lampeter and Llandovery College hold athletics “sports” meetings. 1875 Newport Athletic Club formed and holds “athletic sports.” 1877 Cardiff-born William Gale achieves the phenomenal deed of walking 1,500 miles in 1,000 hours. He was the world’s leading pedestrian. 1879 Llanfair Caereinion Powys-born George Dunning sets a world 40 miles record at Stamford Bridge of 4:50.12. 1880 Newport AC represented by Richard Mullock at the formation of the AAA at The Randolph Hotel, Oxford - Chambers also there. 1881 Dunning effectively sets an inaugural world record for the half-marathon when he runs 1:13.46 on a track at Stamford Bridge. The distance is actually 13 miles 440 yards, i.e. further than the designated half marathon distance of 13 miles 192.5 yards. 1881 Dunning becomes the first Welsh born athlete to win the (English) National cross country title. 1882 Roath (Cardiff) Harriers formed. They amalgamated with Birchgrove (Cardiff) Harriers in 1968 to form Cardiff AAC.1890. 1890 Will Parry, born in Buttington, near Welshpool wins the (English) National cross country title for a third successive year. 1893 First Welsh amateur track championships held as part of an open sports meeting. Just 2 events held - 100 yards and mile won by Charles Thomas (Reading AC) and Hugh Fairlamb (Roath).
    [Show full text]
  • 2019 UCLA CROSS COUNTRY SCHEDULE Colors Blue and Gold Date Meet Location Nickname Bruins Sat, Aug
    2019 UCLA CROSS COUNTRY 2019 QUICK FACTS TABLE OF CONTENTS Location Los Angeles, CA THE 2019 BRUINS 2018 MEET SUMMARIES Athletic Dept. Address 325 Westwood Plaza Table of Contents 2 Meet Recaps 40-41 Los Angeles, CA 90095 TV Roster - Men 3 POSTSEASON HISTORY Athletics Phone (310) 825-8699 TV Roster - Women 4 Ticket Office (310) UCLA-WIN NCAA Championships History 42 Rosters 5 Cross Country Office Phone (310) 794-6443 NCAA West Regional Championships History 43 Coaching Staff 6-8 Chancellor Dr. Gene Block Pac-12 Conference Championships History 44 Athlete Profiles 9-37 Director of Athletics Daniel G. Guerrero UCLA ADMINISTRATION Assoc. Athletic Director (Cross Country) Gavin Crew 2018 RACE TIMES Administrator Biographies 45 Faculty Athletic Rep. Dr. Michael Teitell Meet-by-Meet Results 38-39 Enrollment 44,947 Founded 1919 2019 UCLA CROSS COUNTRY SCHEDULE Colors Blue and Gold Date Meet Location Nickname Bruins Sat, Aug. 31 UCLA vs. UC Riverside Dual Mammoth Lakes, Calif. Conference Pac-12 National Affiliation NCAA Division I Sat, Sept. 28 The Master’s University XC Invite Santa Clarita, Calif. Director of Track & Field/Cross Country Avery Anderson Sat, Sept. 28 Dellinger Invitational Springfield, Ore. Asst. Coach Devin Elizondo Fri, Oct. 18 Nuttycombe Invitational Madison, Wis. Asst. Coach Austin O’Neil Sat, Oct. 19 Santa Clara Bronco Invite Santa Clara, Calif. Volunteer Coach Rob Beamer Fri, Nov. 1 Pac-12 Championships* Monmouth, Ore. 2018 Final National Ranking NR (Men) Fri, Nov. 15 NCAA West Regionals Colfax, Wash. NR (Women) Sat, Nov.
    [Show full text]
  • 2012 European Championships Statistics – Men's 100M
    2012 European Championships Statistics – Men’s 100m by K Ken Nakamura All time performance list at the European Championships Performance Performer Time Wind Name Nat Pos Venue Year 1 1 9.99 1.3 Francis Obikwelu POR 1 Göteborg 20 06 2 2 10.04 0.3 Darren Campbell GBR 1 Budapest 1998 3 10.06 -0.3 Francis Obikwelu 1 München 2002 3 3 10.06 -1.2 Christophe Lemaitre FRA 1sf1 Barcelona 2010 5 4 10.08 0.7 Linford Christie GBR 1qf1 Helsinki 1994 6 10.09 0.3 Linford Christie 1sf1 Sp lit 1990 7 5 10.10 0.3 Dwain Chambers GBR 2 Budapest 1998 7 5 10.10 1.3 Andrey Yepishin RUS 2 Göteborg 2006 7 10.10 -0.1 Dwain Chambers 1sf2 Barcelona 2010 10 10.11 0.5 Darren Campbell 1sf2 Budapest 1998 10 10.11 -1.0 Christophe Lemaitre 1 Barce lona 2010 12 10.12 0.1 Francis Obikwelu 1sf2 München 2002 12 10.12 1.5 Andrey Yepishin 1sf1 Göteborg 2006 14 10.14 -0.5 Linford Christie 1 Helsinki 1994 14 7 10.14 1.5 Ronald Pognon FRA 2sf1 Göteborg 2006 14 7 10.14 1.3 Matic Osovnikar SLO 3 Gö teborg 2006 17 10.15 -0.1 Linford Christie 1 Stuttgart 1986 17 10.15 0.3 Dwain Chambers 1sf1 Budapest 1998 17 10.15 -0.3 Darren Campbell 2 München 2002 20 9 10.16 1.5 Steffen Bringmann GDR 1sf1 Stuttgart 1986 20 10.16 1.3 Ronald Pognon 4 Göteb org 2006 20 9 10.16 1.3 Mark Lewis -Francis GBR 5 Göteborg 2006 20 9 10.16 -0.1 Jaysuma Saidy Ndure NOR 2sf2 Barcelona 2010 24 12 10.17 0.3 Haralabos Papadias GRE 3 Budapest 1998 24 12 10.17 -1.2 Emanuele Di Gregorio IA 2sf1 Barcelona 2010 26 14 10.18 1.5 Bruno Marie -Rose FRA 2sf1 Stuttgart 1986 26 10.18 -1.0 Mark Lewis Francis 2 Barcelona 2010
    [Show full text]
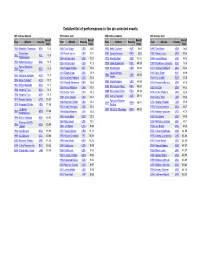
  • Detailed List of Performances in the Six Selected Events
    Detailed list of performances in the six selected events 100 metres women 100 metres men 400 metres women 400 metres men Result Result Result Result Year Athlete Country Year Athlete Country Year Athlete Country Year Athlete Country (sec) (sec) (sec) (sec) 1928 Elizabeth Robinson USA 12.2 1896 Tom Burke USA 12.0 1964 Betty Cuthbert AUS 52.0 1896 Tom Burke USA 54.2 Stanislawa 1900 Frank Jarvis USA 11.0 1968 Colette Besson FRA 52.0 1900 Maxey Long USA 49.4 1932 POL 11.9 Walasiewicz 1904 Archie Hahn USA 11.0 1972 Monika Zehrt GDR 51.08 1904 Harry Hillman USA 49.2 1936 Helen Stephens USA 11.5 1906 Archie Hahn USA 11.2 1976 Irena Szewinska POL 49.29 1908 Wyndham Halswelle GBR 50.0 Fanny Blankers- 1908 Reggie Walker SAF 10.8 1980 Marita Koch GDR 48.88 1912 Charles Reidpath USA 48.2 1948 NED 11.9 Koen 1912 Ralph Craig USA 10.8 Valerie Brisco- 1920 Bevil Rudd SAF 49.6 1984 USA 48.83 1952 Marjorie Jackson AUS 11.5 Hooks 1920 Charles Paddock USA 10.8 1924 Eric Liddell GBR 47.6 1956 Betty Cuthbert AUS 11.5 1988 Olga Bryzgina URS 48.65 1924 Harold Abrahams GBR 10.6 1928 Raymond Barbuti USA 47.8 1960 Wilma Rudolph USA 11.0 1992 Marie-José Pérec FRA 48.83 1928 Percy Williams CAN 10.8 1932 Bill Carr USA 46.2 1964 Wyomia Tyus USA 11.4 1996 Marie-José Pérec FRA 48.25 1932 Eddie Tolan USA 10.3 1936 Archie Williams USA 46.5 1968 Wyomia Tyus USA 11.0 2000 Cathy Freeman AUS 49.11 1936 Jesse Owens USA 10.3 1948 Arthur Wint JAM 46.2 1972 Renate Stecher GDR 11.07 Tonique Williams- 1948 Harrison Dillard USA 10.3 1952 George Rhoden JAM 45.9 2004 BAH 49.41 1976
    [Show full text]
  • 1974 Age Records
    TRACK AGE RECORDS NEWS 1974 TRACK & FIELD NEWS, the popular bible of the sport for 21 years, brings you news and features 18 times a year, including twice a month during the February-July peak season. m THE EXCITING NEWS of the track scene comes to you as it happens, with in-depth coverage by the world's most knowledgeable staff of track reporters and correspondents. A WEALTH OF HUMAN INTEREST FEATURES involving your favor­ ite track figures will be found in each issue. This gives you a close look at those who are making the news: how they do it and why, their reactions, comments, and feelings. DOZENS OF ACTION PHOTOS are contained in each copy, recap­ turing the thrills of competition and taking you closer still to the happenings on the track. STATISTICAL STUDIES, U.S. AND WORLD LISTS AND RANKINGS, articles on technique and training, quotable quotes, special col­ umns, and much more lively reading complement the news and the personality and opinion pieces to give the fan more informa­ tion and material of interest than he'll find anywhere else. THE COMPREHENSIVE COVERAGE of men's track extends from the Compiled by: preps to the Olympics, indoor and outdoor events, cross country, U.S. and foreign, and other special areas. You'll get all the major news of your favorite sport. Jack Shepard SUBSCRIPTION: $9.00 per year, USA; $10.00 foreign. We also offer track books, films, tours, jewelry, and other merchandise & equipment. Write for our Wally Donovan free T&F Market Place catalog. TRACK & FIELD NEWS * Box 296 * Los Altos, Calif.
    [Show full text]
  • “Where the World's Best Athletes Compete”
    6 0 T H A N N U A L “Where the world’s best athletes compete” MEDIA INFORMATION updated on April 5, 2018 6 0 T H A N N U A L “Where the world’s best athletes compete” MEDIA INFORMATION April 5, 2018 Dear Colleagues: The 60th Annual Mt. SAC Relays is set for April 19, 20 and 21, 2018 at Murdock Stadium, on the campus of El Camino College in Torrance, CA. Once again we expect over 5,000 high school, masters, community college, university and other champions from across the globe to participate. We look forward to your attendance. Due to security reasons, ALL MEDIA CREDENTIALS and Parking Permits will be held at the Credential Pick-up area in Parking Lot D, located off of Manhattan Beach Blvd. (please see attached map). Media Credentials and Parking Permit will be available for pick up on: Thursday, April 19 from 2pm - 8pm Friday, April 20 from 8am - 8pm Saturday, April 21 from 8am - 2pm Please present a photo ID to pick up your credentials and then park in lot C which is adjacent to the media credential pick up. Please remember to place your parking pass in your window prior to entering the stadium. The Mt. SAC Relays provides the following services for members of the media: Access to press box, infield and media interview area Access to copies of official results as they become available Complimentary food and beverage for all working media April 20 & 21 WiFi access Additional information including time schedules, dates, times and other important information can be accessed via our website at http://www.mtsacrelays.com If you have any additional questions or concerns, please feel free to call or e-mail me at anytime.
    [Show full text]
  • The Olympic Games, 1904
    Two Athletic Leaders W.H. Liginger, Chairman Olympic Games Committee; Archie Hahn, an Olympic Champion. THEOLYMPIC GAMES 1904 BY CHARLES J. P. LUCAS. ST. LOUIS, MO. Woodward & Tiernan Printing Co. 1905. Copyright, 1905. by Charles J. P. Lucas and E. B. Woodward. St. Louis, Mo. CONTENTS. Preface .................................................. 9 Introduction ........................................... 11 CHAPTER I. America Greets The World ........................... 23 CHAPTER II. Marathon Race ........................................ 45 CHAPTER III. How Records Were Broken ............................ 68 CHAPTER IV East Versus West ...................................... 82 CHAPTER V. Chicago Protests Dewitt ............................ 100 CHAPTER VI. Handicap Competitions .............................. 121 CHAPTER VII. Resume ................................................ 139 ILLUSTRATIONS. 1. Frontispiece “Two Athletic Leaders” 2. Olympic Games Committee. 3. Officials, Olympic Games. 4. Greek Representatives. 5. The Stadium. 6. A Modern Trophy. 7. Individual Point Champion. 8. A Three Time Winner. 9. John Runge, Germany. 10. 4oo Meter Race. 11. A Modern Hercules. 12. Start of Marathon Race. 13. Following the Marathon Race. 14. Thomas J. Hicks. 15. On the Road. 16. Sponging the Winner. 17. Greece Winning the Weight Lift. 18. The Perfect Man, Physically. 19. Standing High Jump. 20. An Easy Victory. 21. International Team Race. 22. World’s Discus Champion. 23. Charles Dvorak, Pole Vaulting. 24. 110 Meter High Hurdles. 25. Tug Of War. 26. Finish of 60 Yard Dash. 27. Ireland Wins the Mile Run. 28. Defending His Title. PREFACE. N presenting “The Olympic Games, 1904, ” the I author has made no attempt to consider the sports held before them, as the Olympic Games were those events which opened August 29, continuing up to, and including, the games contested September 3. The Olympic Games Com- mittee, consisting of James E.
    [Show full text]