Designing a Practical Code-Based Signature Scheme from Zero-Knowledge Proofs with Trusted Setup
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Java (Programming Langua a (Programming Language)
Java (programming language) From Wikipedia, the free encyclopedialopedia "Java language" redirects here. For the natural language from the Indonesian island of Java, see Javanese language. Not to be confused with JavaScript. Java multi-paradigm: object-oriented, structured, imperative, Paradigm(s) functional, generic, reflective, concurrent James Gosling and Designed by Sun Microsystems Developer Oracle Corporation Appeared in 1995[1] Java Standard Edition 8 Update Stable release 5 (1.8.0_5) / April 15, 2014; 2 months ago Static, strong, safe, nominative, Typing discipline manifest Major OpenJDK, many others implementations Dialects Generic Java, Pizza Ada 83, C++, C#,[2] Eiffel,[3] Generic Java, Mesa,[4] Modula- Influenced by 3,[5] Oberon,[6] Objective-C,[7] UCSD Pascal,[8][9] Smalltalk Ada 2005, BeanShell, C#, Clojure, D, ECMAScript, Influenced Groovy, J#, JavaScript, Kotlin, PHP, Python, Scala, Seed7, Vala Implementation C and C++ language OS Cross-platform (multi-platform) GNU General Public License, License Java CommuniCommunity Process Filename .java , .class, .jar extension(s) Website For Java Developers Java Programming at Wikibooks Java is a computer programming language that is concurrent, class-based, object-oriented, and specifically designed to have as few impimplementation dependencies as possible.ble. It is intended to let application developers "write once, run ananywhere" (WORA), meaning that code that runs on one platform does not need to be recompiled to rurun on another. Java applications ns are typically compiled to bytecode (class file) that can run on anany Java virtual machine (JVM)) regardless of computer architecture. Java is, as of 2014, one of tthe most popular programming ng languages in use, particularly for client-server web applications, witwith a reported 9 million developers.[10][11] Java was originallyy developed by James Gosling at Sun Microsystems (which has since merged into Oracle Corporation) and released in 1995 as a core component of Sun Microsystems'Micros Java platform. -

Thesis.Pdf (PDF, 656Kb)
Extending old languages for new architectures Leo P. White University of Cambridge Computer Laboratory Queens' College October 2012 This dissertation is submitted for the degree of Doctor of Philosophy Declaration This dissertation is the result of my own work and includes nothing which is the outcome of work done in collaboration except where specifically indicated in the text. This dissertation does not exceed the regulation length of 60 000 words, including tables and footnotes. Extending old languages for new architectures Leo P. White Summary Architectures evolve quickly. The number of transistors available to chip designers doubles every 18 months, allowing increasingly complex architectures to be developed on a single chip. Power dissipation issues have forced chip designers to look for new ways to use the transistors at their disposal. This situation inevitably leads to new architectural features on a fairly regular basis. Enabling programmers to benefit from these new architectural features can be problematic. Since architectures change frequently, and compilers last for a long time, it is clear that compilers should be designed to be extensible. This thesis argues that to support evolving architectures a compiler should support the creation of high-level language extensions. In particular, it must support extending the compiler's middle-end. We describe the design of EMCC, a C compiler that allows extension of its front-, middle- and back-ends. OpenMP is an extension to the C programming language to support parallelism. It has recently added support for task-based parallelism, a dynamic form of parallelism made popular by Cilk. However, implementing task-based parallelism efficiently requires much more involved program transformation than the simple static parallelism originally supported by OpenMP. -

Evaluation of On-Ramp Control Algorithms
CALIFORNIA PATH PROGRAM INSTITUTE OF TRANSPORTATION STUDIES UNIVERSITY OF CALIFORNIA, BERKELEY Evaluation of On-ramp Control Algorithms Michael Zhang, Taewan Kim, Xiaojian Nie, Wenlong Jin University of California, Davis Lianyu Chu, Will Recker University of California, Irvine California PATH Research Report UCB-ITS-PRR-2001-36 This work was performed as part of the California PATH Program of the University of California, in cooperation with the State of California Business, Transportation, and Housing Agency, Department of Transportation; and the United States Department of Transportation, Federal Highway Administration. The contents of this report reflect the views of the authors who are responsible for the facts and the accuracy of the data presented herein. The contents do not necessarily reflect the official views or policies of the State of California. This report does not constitute a standard, specification, or regulation. Final Report for MOU 3013 December 2001 ISSN 1055-1425 CALIFORNIA PARTNERS FOR ADVANCED TRANSIT AND HIGHWAYS Evaluation of On-ramp Control Algorithms September 2001 Michael Zhang, Taewan Kim, Xiaojian Nie, Wenlong Jin University of California at Davis Lianyu Chu, Will Recker PATH Center for ATMS Research University of California, Irvine Institute of Transportation Studies One Shields Avenue University of California, Davis Davis, CA 95616 ACKNOWLEDGEMENTS Technical assistance on Paramics simulation from the Quadstone Technical Support sta is also gratefully acknowledged. ii EXECUTIVE SUMMARY This project has three objectives: 1) review existing ramp metering algorithms and choose a few attractive ones for further evaluation, 2) develop a ramp metering evaluation framework using microscopic simulation, and 3) compare the performances of the selected algorithms and make recommendations about future developments and eld tests of ramp metering systems. -

Volume 8 Issue 3
INFOLINE EDITORIAL BOARD EXECUTIVE COMMITTEE Chief Patron : Thiru A.K.Ilango Correspondent Patron : Dr. N.Raman, M.Com., M.B.A., M.Phil., Ph.D., Principal Editor in Chief : Mr. S.Muruganantham, M.Sc., M.Phil., Head of the Department STAFF ADVISOR Ms. P.Kalarani M.Sc., M.C.A., M.Phil., Assistant Professor, Department of Computer Technology and Information Technology STAFF EDITOR Ms. C.Indrani M.C.A., M.Phil., Assistant Professor, Department of Computer Technology and Information Technology STUDENT EDITORS B.Mano Pretha III B.Sc. (Computer Technology) K.Nishanthan III B.Sc. (Computer Technology) P.Deepika Rani III B.Sc. (Information Technology) R.Pradeep Rajan III B.Sc. (Information Technology) D.Harini II B.Sc. (Computer Technology) V.A.Jayendiran II B.Sc. (Computer Technology) S.Karunya II B.Sc. (Information Technology) E.Mohanraj II B.Sc. (Information Technology) S.Aiswarya I B.Sc. (Computer Technology) A.Tamilhariharan I B.Sc. (Computer Technology) P.Vijaya shree I B.Sc. (Information Technology) S.Prakash I B.Sc. (Information Technology) CONTENTS Nano Air Vehicle 1 Reinforcement Learning 2 Graphics Processing Unit (GPU) 4 The History of C Programming 5 Fog Computing 7 Big Data Analytics 9 Common Network Problems 14 Bridging the Human-Computer Interaction 15 Adaptive Security Architecture 16 Digital Platform ` 16 Mesh App and Service Architecture 17 Blockchain Technology 18 Digital Twin 20 Puzzles 21 Riddles 22 right, forward and backward, rotate clockwise NANO AIR VEHICLE (NAV) and counter-clockwise; and hover in mid-air. The artificial hummingbird using its flapping The AeroVironment Nano wings for propulsion and attitude control. -

Fundamental Data Structures Contents
Fundamental Data Structures Contents 1 Introduction 1 1.1 Abstract data type ........................................... 1 1.1.1 Examples ........................................... 1 1.1.2 Introduction .......................................... 2 1.1.3 Defining an abstract data type ................................. 2 1.1.4 Advantages of abstract data typing .............................. 4 1.1.5 Typical operations ...................................... 4 1.1.6 Examples ........................................... 5 1.1.7 Implementation ........................................ 5 1.1.8 See also ............................................ 6 1.1.9 Notes ............................................. 6 1.1.10 References .......................................... 6 1.1.11 Further ............................................ 7 1.1.12 External links ......................................... 7 1.2 Data structure ............................................. 7 1.2.1 Overview ........................................... 7 1.2.2 Examples ........................................... 7 1.2.3 Language support ....................................... 8 1.2.4 See also ............................................ 8 1.2.5 References .......................................... 8 1.2.6 Further reading ........................................ 8 1.2.7 External links ......................................... 9 1.3 Analysis of algorithms ......................................... 9 1.3.1 Cost models ......................................... 9 1.3.2 Run-time analysis -

Comparative Studies of Six Programming Languages
Comparative Studies of Six Programming Languages Zakaria Alomari Oualid El Halimi Kaushik Sivaprasad Chitrang Pandit Concordia University Concordia University Concordia University Concordia University Montreal, Canada Montreal, Canada Montreal, Canada Montreal, Canada [email protected] [email protected] [email protected] [email protected] Abstract Comparison of programming languages is a common topic of discussion among software engineers. Multiple programming languages are designed, specified, and implemented every year in order to keep up with the changing programming paradigms, hardware evolution, etc. In this paper we present a comparative study between six programming languages: C++, PHP, C#, Java, Python, VB ; These languages are compared under the characteristics of reusability, reliability, portability, availability of compilers and tools, readability, efficiency, familiarity and expressiveness. 1. Introduction: Programming languages are fascinating and interesting field of study. Computer scientists tend to create new programming language. Thousand different languages have been created in the last few years. Some languages enjoy wide popularity and others introduce new features. Each language has its advantages and drawbacks. The present work provides a comparison of various properties, paradigms, and features used by a couple of popular programming languages: C++, PHP, C#, Java, Python, VB. With these variety of languages and their widespread use, software designer and programmers should to be aware -

Comparative Programming Languages CM20253
We have briefly covered many aspects of language design And there are many more factors we could talk about in making choices of language The End There are many languages out there, both general purpose and specialist And there are many more factors we could talk about in making choices of language The End There are many languages out there, both general purpose and specialist We have briefly covered many aspects of language design The End There are many languages out there, both general purpose and specialist We have briefly covered many aspects of language design And there are many more factors we could talk about in making choices of language Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important For example, can you easily join together code written in Java and C? The End Or languages And then the interopability of languages becomes important For example, can you easily join together code written in Java and C? The End Or languages Often a single project can use several languages, each suited to its part of the project For example, can you easily join together code written in Java and C? The End Or languages Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important The End Or languages Often a single project can use several languages, each suited to its part of the project And then the interopability of languages becomes important For example, can you easily -

List of File Formats - Wikipedia, the Free Encyclopedia
List of file formats - Wikipedia, the free encyclopedia http://en.wikipedia.org/w/index.php?title=List_of_file_fo... List of file formats From Wikipedia, the free encyclopedia See also: List of file formats (alphabetical) This is a list of file formats organized by type, as can be found on computers. Filename extensions are usually noted in parentheses if they differ from the format name or abbreviation. In theory, using the basic Latin alphabet (A–Z) and an extension of up to three single-cased letters, 18,279 combinations can be made (263+262+261+260). When other acceptable characters are accepted, the maximum number is increased (very possibly to a number consisting of at least six digits). Many operating systems do not limit filenames to a single extension shorter than 4 characters, like what was common with some operating systems that supported the FAT file system. Examples of operating systems that don't have such a small limit include Unix-like systems. Also, Microsoft Windows NT, 95, 98, and Me don't have a three character limit on extensions for 32-bit or 64-bit applications on file systems other than pre-Windows 95/Windows NT 3.5 versions of the FAT file system. Some filenames are given extensions longer than three characters. Contents 1 Archive and compressed 1.1 Physical recordable media archiving 2 Computer-aided 2.1 Computer-aided design (CAD) 2.2 Electronic design automation (EDA) 2.3 Test technology 3 Database 4 Desktop publishing 5 Document 6 Font file 7 Geographic information system 8 Graphical information organizers -

Remote Electronic Monitor System Design for Distributed Application in Depending on Wide Network
جامعة حلب كلية الهندسة الكهربائية واﻻلكترونية قسم الهندسة اﻹلكترونية --------------------------------------------------------------------------------------------------------------------- ﻹ Remote Electronic Monitor System Design for Distributed Application in Depending on Wide Network Case Study: Cotton Marketing Organization أطروحة لنيل درجة الماجستير في الهندسة اﻹلكترونية اعداد المهندس : عبد القادر موالدي 7341 هـ / 6172 م جامعة حلب كلية الهندسة الكهربائية واﻻلكترونية قسم الهندسة اﻹلكترونية ----------------------------------------------------------------------------------------------------------------------- ﻹ Remote Electronic Monitor System Design for Distributed Application in Depending on Wide Network Case Study: Cotton Marketing Organization أطروحة لنيل درجة الماجستير في الهندسة اﻹلكترونية اعداد الطالب المهندس : عبد القادر موالدي الدكتور محمد المحمد رئيس قسم الهندسة اﻹلكترونية – مشرف رئيسي 7341 هـ / 6172 م قدمت هذه الرسالة استكماﻻً ملتلباا نيل درجة املاجستري يف قسم اهلدندسة اﻹلكرتونية ، كبية اهلدندسة الكهربائية واﻹلكرتونية ، جامعة حبب شهادة نشههههههههههد بههمو ال مههل الموطهههههههوف في هههث امطروحههة هو نتيجههة بحهه ع مي قههام بهه المرشههههههه املهدندس عاد القادر موالدي ، تحت اشراف الدكتور املهدندس حممد احملمد في قسم الهندسة اﻹلكترونية مو ك ي الهندسهههههههة الكهربائية واﻹلكترونية بجام ة ح ب ي وأو أي مراجع أخرى ثكرت في هثا البح موثقة في نص الرسالة . المرش المشرف الرئيسي المهندس عبد القادر موالدي الدكتور المهندس محمد المحمد Testimony We witness that the work described in this thesis is the result of scientific search conducted by the candidate Eng. Abdul Kader Mawaldi under the main supervision of Dr. Mohammad Al-Mohammad at the electronic department, faculty of Electrical and Electronic Engineering, University of Aleppo. Any other references mentioned in this work, have been documented in the thesis text. Candidate Main Supervision Eng. Abdul Kader Mawaldi Dr. Mohammad Al-Mohammad تصريح أطرح بمو هثا البح ب نواو: لم يسبق أو ق بل ل حطول ع ى أي شهادة ي وﻻ هو مقدم ل حطول ع ى أي شهادة أخرى . -

Modern Extensible Languages
Modern Extensible Languages Daniel Zingaro October 2007 SQRL Report 47 McMaster University Abstract Extensible languages are programming languages that allow a user to modify or add syntax, and associate the new syntactic forms with semantics. What are these languages good for? What kinds of features are easy to add, and which are not? Are they powerful enough to be taken seriously? In this survey we will attempt to answer such questions as we consider procedural, object-oriented, functional and general-purpose extensible languages. We are primarily interested in expressive power (regular, context-free), associated caveats (unhygienic, ambiguity) and ease of use of the various mechanisms. 1 What is an Extensible Language? Before beginning, it is essential to have an operational definition of what exactly constitutes an extensible language; this will dictate the flow of the remainder of the paper. Standish [23] gives a rather broad definition, stating simply: an extensible language allows users to define new language features. These features may include new notation or operations, new or modified control structures, or even elements from different programming paradigms. To facilitate discussion, it is helpful to adopt Standish's nomenclature, and divide this spectrum of features into three classes: paraphrase, orthophrase and metaphrase. Paraphrase refers to adding new features by relying on features already present in the language; a prototypical example is defining macros, which of course ultimately expand into the programming language's standard syntax. Orthophase refers to adding features not expressible in terms of available language primitives; for example, adding an I/O system to a language that lacks one. -
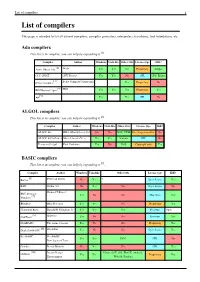
List of Compilers 1 List of Compilers
List of compilers 1 List of compilers This page is intended to list all current compilers, compiler generators, interpreters, translators, tool foundations, etc. Ada compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? [2] Aonix Object Ada Atego Yes Yes Yes Proprietary Eclipse GCC GNAT GNU Project Yes Yes No GPL GPS, Eclipse [3] Irvine Compiler Irvine Compiler Corporation Yes Proprietary No [4] IBM Rational Apex IBM Yes Yes Yes Proprietary Yes [5] A# Yes Yes GPL No ALGOL compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? ALGOL 60 RHA (Minisystems) Ltd No No DOS, CP/M Free for personal use No ALGOL 68G (Genie) Marcel van der Veer Yes Yes Various GPL No Persistent S-algol Paul Cockshott Yes No DOS Copyright only Yes BASIC compilers This list is incomplete; you can help by expanding it [1]. Compiler Author Windows Unix-like Other OSs License type IDE? [6] BaCon Peter van Eerten No Yes ? Open Source Yes BAIL Studio 403 No Yes No Open Source No BBC Basic for Richard T Russel [7] Yes No No Shareware Yes Windows BlitzMax Blitz Research Yes Yes No Proprietary Yes Chipmunk Basic Ronald H. Nicholson, Jr. Yes Yes Yes Freeware Open [8] CoolBasic Spywave Yes No No Freeware Yes DarkBASIC The Game Creators Yes No No Proprietary Yes [9] DoyleSoft BASIC DoyleSoft Yes No No Open Source Yes FreeBASIC FreeBASIC Yes Yes DOS GPL No Development Team Gambas Benoît Minisini No Yes No GPL Yes [10] Dream Design Linux, OSX, iOS, WinCE, Android, GLBasic Yes Yes Proprietary Yes Entertainment WebOS, Pandora List of compilers 2 [11] Just BASIC Shoptalk Systems Yes No No Freeware Yes [12] KBasic KBasic Software Yes Yes No Open source Yes Liberty BASIC Shoptalk Systems Yes No No Proprietary Yes [13] [14] Creative Maximite MMBasic Geoff Graham Yes No Maximite,PIC32 Commons EDIT [15] NBasic SylvaWare Yes No No Freeware No PowerBASIC PowerBASIC, Inc. -

Method of Paradigmatic Analysis of Programming Languages and Systems
Method of Paradigmatic Analysis of Programming Languages and Systems Lidia Gorodnyaya1,2[0000-0002-4639-9032] 1 A.P. Ershov Institute of Informatics Systems (IIS), 6, Acad. Lavrentjev pr., Novosibirsk 630090, Russia 2 Novosibirsk State University, Pirogov str., 2, Novosibirsk 630090, Russia [email protected] Abstract. The purpose of the article is to describe the method of comparison of programming languages, convenient for assessing the expressive power of languages and the complexity of the programming systems. The method is adapted to substantiate practical, objective criteria of program decomposition, which can be considered as an approach to solving the problem of factorization of very complicated definitions of programming languages and their support systems. In addition, the article presents the results of the analysis of the most well-known programming paradigms and outlines an approach to navigation in the modern expanding space of programming languages, based on the classification of paradigms on the peculiarities of problem statements and semantic characteristics of programming languages and systems with an emphasis on the criteria for the quality of programs and priorities in decision- making in their implementation. The proposed method can be used to assess the complexity of programming, especially if supplemented by dividing the requirements of setting tasks in the fields of application into academic and industrial, and by the level of knowledge into clear, developed and complicated difficult to certify requirements. Keywords: Definition of Programming Languages, Programming Paradigms, Definition Decomposition Criteria, Semantic Systems 1 Introduction Descriptions of modern programming languages (PL) usually contain a list of 5-10 predecessors and a number of programming paradigms (PP) supported by the language [1,2].