DOCSLIB.ORG

Section 6 : ISI & Pulse Shaping

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Section 6 : ISI & Pulse Shaping CS3282 Section 6 6.1 BMGC/ 25/08/06 University of Manchester School of Computer Science CS3282: Digital Communications ’05-06 Section 6: Inter-symbol interference and pulse shaping Rectangular symbols are not suitable for transmitting data at the highest possible bit-rates over band- limited channels. A rectangular pulse or any other shaped pulse which is time-limited (i.e. is non-zero for a finite period of time, say T seconds) will require infinite bandwidth if it is not to be distorted, possibly unrecognizably. A symbol with finite bandwidth must have, in theory, infinite time duration. Although using a symbol which really does exist from t = -∞ to t = +∞ to send a single “1” or a “0” (or maybe two or three of them if we are using multi-level signaling) may seem impossible in practice, we have to keep this in mind as an ideal and produce approximations to this form of signaling. The pulses we use in practice may not actually go on, and back in time for ever. But they must definitely be non- zero for considerably more than T seconds when the signaling rate is 1/T symbols per second. Inevitably this means that one symbol will run into the previous and next symbol, and significantly affect several more besides. The result could be “inter-symbol interference” (ISI) where the data conveyed by one symbol causes the data of other symbols to be misinterpreted. Although we cannot avoid the overlap of symbols in the time-domain, we must find ways of making sure that the data carried by the symbols is not affected by this overlap. The solution to this challenge lies in “pulse shaping” which means that we must carefully choose the time-domain shape of the symbols and hence their spectral shape. A convenient way of generating symbols with the time-domain shape we require is to generate an impulse of the appropriate strength for each symbol and then to shape this impulse by passing it through a “shaping” filter. The impulse-response of the shaping filter is the symbol shape we wish to launch into the channel. An FIR digital filter followed by a digital to analogue converter will do this job nicely. The channel will inevitably affect the shape of the symbol and noise will be added. At the receiver, to optimize the detection process, filtering tasks are required as illustrated below. Samples at A 3A -A intervals T Shaping Matched Equal- Channel T T Filter filter iser n(t) CS3282 Section 6 6.2 BMGC/ 25/08/06 Inter-symbol interference (ISI) can occur due to the ringing of one symbol into the next. However, ISI can be avoided if the transmitter's pulse shaping filter shapes the symbols so that zero-crossings at the output of the receiving filters occur T seconds, 2T seconds, and so on after (and before) the centre of the symbol. So when we sample at t=0, T, 2T, etc, we only see the centre of one symbol, all the other symbols being zero at those instants. This is nice in theory and possible to a fair degree in practice. If we combine the transmitter's shaping filter, the channel and the receiving filters (i.e. the matched filter and the equaliser) into a single frequency-response HN((ƒ)) say, then our goal is achieved if HN((ƒ)) is a “Nyquist frequency-response". To be a classed as a 'Nyquist frequency-response', as well as band- limiting from -1/T to 1/T Hz, HN((f)) must have a form of odd-symmetry about 1/(2T ) in that: * H N (( f )) + H N ()1/T − f = cons tant for 0 ≤ | f | ≤ 1 T Two purely real frequency-responses satisfying this property are shown below. It may be shown (Exercise 6.2 below) that this property guarantees that the impulse-response corresponding to HN((f)) , i.e. its inverse Fourier transform, has zero crossings at t = ±T, ±2T, ±3T, …. |HN((ƒ))| 1 0.5 ƒ -1/T -1/2T 0 1/4T 1/2T 3/4T 1/T 1 : | f |< 1/(2T) The “brick-wall” filter: H B (( f )) = 0 : | f |≥ 1/(2T) has the property of having a 'Nyquist frequency-response' and we already know that its impulse response is a sinc function with zero crossings at t = ±T, ±2T, etc. The 'brick-wall' frequency- response achieves the required zero-crossing property with the minimum possible bandwidth, but is difficult to deal with because the side-lobes of its "sinc" impulse response do not die away very quickly. To design a pulse-shaping filter with a reasonable approximation to this 'brick-wall' frequency-response, we would need a very long impulse-response and hence a high order FIR digital filter. Also, assuming we could implement a good enough approximation, if there is the slightest error in the timing of our sampling point, significant ISI will occur. CS3282 Section 6 6.3 BMGC/ 25/08/06 Raised cosine frequency response A commonly used family of Nyquist frequency-responses is a range of “raised cosine” frequency- responses parameterized by r (sometimes called α) and defined by the following formula: 1 : | f | ≤ (1− r) /(2T) H rc (( f )) = 0.5[1+ cos(πT{| f | −(1− r) /(2T)}/ r)] : (1− r) /(2T) ≤ | f | ≤ (1+ r) /(2T) 0 : (1+ r) /(2T) <| f | The impulse-response of a filter with such a frequency-response may be shown to be: sin c(t /T )cos(πrt /T) sin(πx) h(t) = where sinc(x) = lim T − 4r 2t 2 /T πx When r=0, this becomes the “brick-wall” filter mentioned earlier with the narrowest bandwidth of all the family: -1/(2T) to 1/(2T) Hz. When r = 0.5, Hrc(f) is as shown below, assuming T=0.001 seconds so that the symbol rate 1/T = 1 kHz.. From the general formula above, its spectrum is: 1 : | f | ≤ 250 Hz H rc (( f )) = 0.5[1+ cos(2π{| f | −250}/1000)] : 250 ≤ | f | ≤ 750 0 : 750 < | f | 1.2 1 50%RC spectrum 0.8 0.6 Modulus 0.4 0.2 0 Frequency -1000 -750 -500 -250 0 250 500 750 1000 In the graph above, drawn using "Microsoft Excel" , note the "odd-symmetry" about f=500 Hz for f >0 and about f = -500 Hz = - 1/(2T) for f <0. It may be shown that Hrc((f)) + H*rc(( 1000 - f ) ) = 1. CS3282 Section 6 6.4 BMGC/ 25/08/06 When r=1, Hrc((ƒ)) becomes a pure raised cosine shaped frequency-response with no “flat-top” and the widest bandwidth of the family: -1/T to 1/T Hz. With 1/T=1 kHz, the bandwidth would be -1000 to 1000 Hz. The impulse-responses hrc(t) corresponding to Hrc((ƒ)) with r=0 and r=1 are shown below taking T to be 10 seconds. Such graphs are easily drawn using a spreadsheet such as Microsoft Excel or MATLAB. Notice the reduction of side-lobe ripples when r=1, but this is at the expense of a doubling of the bandwidth. A raised cosine spectrally shaped pulse with a given value of r is called a "100r per- cent RC symbol" and has band-width from -(1+r)/T Hz to (1+r)/T. When r=0.5, we have a 50% RC spectrally shaped symbol (see spectrum above) with bandwidth from -750 Hz to 750 Hz if 1/T = 1 kHz.. This is 50% more than the absolute minimum band-width needed to avoid ISI with the techniques discussed up to now. The minimum bandwidth would be achieved with a 0% RC symbol which has a "brick-wall" spectrum from -1/(2T) to +1/(2T) Hz. Apart from the practical difficulties of generating a pulse with such a spectrum, the disadvantage of the brick-wall spectrum , as mentioned above, is that its time-domain shape is a "sinc" pulse which does not die away quickly enough for our liking. The 100% RC spectrum (r=1) produces a time-domain pulse which dies away much faster. So by increasing r from 0 to 1 we improve the rate of dying away at the expense of extra bandwidth. 0.1 0.08 0.06 h(t) for T=10, r=0 & 1 0.04 0.02 0 -40 -30 -20 -10 0 10 20 30 40 -0.02 t A good way to implement a shaping filter is to use an FIR digital filter with multiplier coefficients equal to samples of h(t). A succession of shaped pulses generated by a the transmission of a continuous bit-stream are often viewed on an oscilloscope as “eye-diagrams”. The oscilloscope is CS3282 Section 6 6.5 BMGC/ 25/08/06 triggered approximately at the beginning of each pulse, and an open eye is hopefully seen as each new shaped pulse is superimposed on the previous pulses. If noise is added, the eye is seen to close, making threshold comparisons for detection difficult. Remember that HN((ƒ)) is the required overall response of transmitting filter, channel and receiving filters. Within the receiver an equalising filter is introduced to cancel out the filtering effect of the channel. We discuss this later. If the overall symbol pulse shape as seen at the output of the receiving filters is to have a raised cosine spectrum and the receiving filters include a matched filter, it would not be correct for the transmitter to send symbols with raised cosine spectra. If we did send such a symbol its matched filter would have gain-response equal to the magnitude spectrum of the pulse, and the resulting output would have this spectrum squared.
Load more

Recommended publications
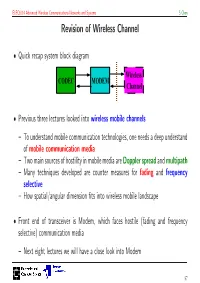
  • Revision of Wireless Channel
    ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Revision of Wireless Channel • Quick recap system block diagram Wireless CODEC MODEM Channel • Previous three lectures looked into wireless mobile channels – To understand mobile communication technologies, one needs a deep understand of mobile communication media – Two main sources of hostility in mobile media are Doppler spread and multipath – Many techniques developed are counter measures for fading and frequency selective – How spatial/angular dimension fits into wireless mobile landscape • Front end of transceiver is Modem, which faces hostile (fading and frequency selective) communication media – Next eight lectures we will have a close look into Modem 57 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Digital Modulation Overview In Digital Coding and Transmission, we learn schematic of MODEM (modulation and demodulation) • with its basic components: clock carrier pulse b(k) x(k) x(t) s(t) pulse Tx filter bits to modulat. symbols generator GT (f) clock carrier channel recovery recovery GC (f) ^ b(k) x(k)^x(t) ^s(t) ^ symbols sampler/ Rx filter AWGN demodul. + to bits decision GR (f) n(t) The purpose of MODEM: transfer the bit stream at required rate over the communication medium • reliably – Given system bandwidth and power resource 58 ELEC6214 Advanced Wireless Communications Networks and Systems S Chen Constellation Diagram • Digital modulation signal has finite states. This manifests in symbol (message) set: M = {m1, m2, ··· , mM }, where each symbol contains log2 M bits • Or in modulation signal set: S = {s1(t),s2(t), ··· sM (t)}. There is one-to-one relationship between two sets: modulation scheme M S ←→ Q • Example: BPSK, M = 2.
    [Show full text]
  • Pulse Shape Filtering in Wireless Communication-A Critical Analysis
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 2, No.3, March 2011 Pulse Shape Filtering in Wireless Communication-A Critical Analysis A. S Kang Vishal Sharma Assistant Professor, Deptt of Electronics and Assistant Professor, Deptt of Electronics and Communication Engg Communication Engg SSG Panjab University Regional Centre University Institute of Engineering and Technology Hoshiarpur, Punjab, INDIA Panjab University Chandigarh - 160014, INDIA [email protected] [email protected] Abstract—The goal for the Third Generation (3G) of mobile networks. The standard that has emerged is based on ETSI's communications system is to seamlessly integrate a wide variety Universal Mobile Telecommunication System (UMTS) and is of communication services. The rapidly increasing popularity of commonly known as UMTS Terrestrial Radio Access (UTRA) mobile radio services has created a series of technological [1]. The access scheme for UTRA is Direct Sequence Code challenges. One of this is the need for power and spectrally Division Multiple Access (DSCDMA). The information is efficient modulation schemes to meet the spectral requirements of spread over a band of approximately 5 MHz. This wide mobile communications. Pulse shaping plays a crucial role in bandwidth has given rise to the name Wideband CDMA or spectral shaping in the modern wireless communication to reduce WCDMA.[8-9] the spectral bandwidth. Pulse shaping is a spectral processing technique by which fractional out of band power is reduced for The future mobile systems should support multimedia low cost, reliable , power and spectrally efficient mobile radio services. WCDMA systems have higher capacity, better communication systems. It is clear that the pulse shaping filter properties for combating multipath fading, and greater not only reduces inter-symbol interference (ISI), but it also flexibility in providing multimedia services with defferent reduces adjacent channel interference.
    [Show full text]
  • Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
    Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse.
    [Show full text]
  • ECE 463 Lab 3: Pulse Shaping and Matched Filtering
    UIUC ECE 463 Digital Communication Laboratory Fall 2018 ECE 463 Lab 3: Pulse Shaping and Matched Filtering 1. Introduction The objective of this lab session is to introduce the basic concepts of pulse shaping, matched filter and pulse alignment. In digital communication, the message in digital must be converted into an analog signal to be transmitted. This conversion is done by the pulse shaping filter, which changes each symbol into a suitable analog pulse. Designing the pulse shape is important because the spectrum of the pulse dictates the spectrum of the whole transmission. However, to confine the spectrum, we have to smooth the pulse with slow transition. This requires the pulse extending beyond a symbol time, which introduces inter- symbol interference (ISI). Thus, there is a trade-off between the bandwidth and the ISI of the pulse shape. After transmission, the matched filter helps to recapture the symbols from the received pulses. The matched filter is aimed at reducing the sensitivity of noise by maximizing the signal-to-noise ratio (SNR) and minimizing the ISI at the receiver. In a more realistic channel model, the receiver never knows the precise arrival time of the pulse. Therefore, the receiver must know the exact symbol timing in order to correctly demodulate the transmitted symbols from the transmitter. 1.1. Contents 1. Introduction 2. Pulse Shaping 3. Matched Filtering 4. Pulse Alignment (Symbol Timing Recovery) 1.2. Report Submit the answers, figures and the discussions on all the questions. The report is due as a hard copy at the beginning of the next lab.
    [Show full text]
  • Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems
    Root Raised Cosine (RRC) Filters and Pulse Shaping in Communication Systems Erkin Cubukcu Abstract This presentation briefly discusses application of the Root Raised Cosine (RRC) pulse shaping in the space telecommunication. Use of the RRC filtering (i.e., pulse shaping) is adopted in commercial communications, such as cellular technology, and used extensively. However, its use in space communication is still relatively new. This will possibly change as the crowding of the frequency spectrum used in the space communication becomes a problem. The two conflicting requirements in telecommunication are the demand for high data rates per channel (or user) and need for more channels, i.e., more users. Theoretically as the channel bandwidth is increased to provide higher data rates the number of channels allocated in a fixed spectrum must be reduced. Tackling these two conflicting requirements at the same time led to the development of the RRC filters. More channels with wider bandwidth might be tightly packed in the frequency spectrum achieving the desired goals. A link model with the RRC filters has been developed and simulated. Using 90% power Bandwidth (BW) measurement definition showed that the RRC filtering might improve spectrum efficiency by more than 75%. Furthermore using the matching RRC filters both in the transmitter and receiver provides the improved Bit Error Rate (BER) performance. In this presentation the theory of three related concepts, namely pulse shaping, Inter Symbol Interference (ISI), and Bandwidth (BW) will be touched
    [Show full text]
  • Digital Phase Modulation: a Review of Basic Concepts
    Digital Phase Modulation: A Review of Basic Concepts James E. Gilley Chief Scientist Transcrypt International, Inc. [email protected] August , Introduction The fundamental concept of digital communication is to move digital information from one point to another over an analog channel. More specifically, passband dig- ital communication involves modulating the amplitude, phase or frequency of an analog carrier signal with a baseband information-bearing signal. By definition, fre- quency is the time derivative of phase; therefore, we may generalize phase modula- tion to include frequency modulation. Ordinarily, the carrier frequency is much greater than the symbol rate of the modulation, though this is not always so. In many digital communications systems, the analog carrier is at a radio frequency (RF), hundreds or thousands of MHz, with information symbol rates of many megabaud. In other systems, the carrier may be at an audio frequency, with symbol rates of a few hundred to a few thousand baud. Although this paper primarily relies on examples from the latter case, the concepts are applicable to the former case as well. Given a sinusoidal carrier with frequency: fc , we may express a digitally-modulated passband signal, S(t), as: S(t) A(t)cos(2πf t θ(t)), () = c + where A(t) is a time-varying amplitude modulation and θ(t) is a time-varying phase modulation. For digital phase modulation, we only modulate the phase of the car- rier, θ(t), leaving the amplitude, A(t), constant. BPSK We will begin our discussion of digital phase modulation with a review of the fun- damentals of binary phase shift keying (BPSK), the simplest form of digital phase modulation.
    [Show full text]
  • Spline Pulse Shaping with Isi-Free Matched Filter Receiver
    SPLINE PULSE SHAPING WITH ISI-FREE MATCHED FILTER RECEIVER Jes´usIb´a˜nez, Carlos Pantale´on, Jos´eDiez, Ignacio Santamar´ıa DICOM, ETSII y Telecomunicaci´on,Universidad de Cantabria. Avda Los Castros s.n., 39005 Santander, Spain. Tel: +34 942 201388; fax: +34 942 201488 e-mail:[email protected] ∗ ABSTRACT idea, in this paper we propose to interpolate the discrete se- Although the raised cosine pulse shaping filter is a well- quence of symbols using splines. In this way, we construct an established standard in digital communications, in many ISI-free signal when sampled at the symbol rate. Although practical systems simpler approaches are useful. In this any reconstruction technique from the communications sym- paper a new family of pulse shaping filters with zero in- bols that exactly goes through the symbols is a zero ISI tersymbol interference after matched filtering is proposed. communications signal, splines have a number of advantages The method, based on the spline interpolation of the symbol that make them an interesting choice when spectral con- data, exploits two properties of splines: that the B-spline tent as well as complexity are of concern. The main advan- coefficients can be efficiently obtained via digital filtering, tage is that any spline interpolation model of odd-order may and that the B-spline kernels of order n can be constructed be computed by filtering the sequence of symbols with two from the convolution of n + 1 rectangular pulses. These matched filters, so it is quite simple to design an optimal re- two facts suggest how to decompose the filtering operations ceiver.
    [Show full text]
  • PAM Communication System Impulse Modulator
    PAM Communication System {Ex: -3,-1,1,3} Binary Impulse Pulse message Mapping Modulation sequence Modulator Shaping π Cos(2 fct) Digital data transmission using pulse amplitude modulation (PAM) Bit rate Rd bits/sec Input bits are blocked into J-bit words and mapped into the sequence of symbols mk which are selected from an alphabet of M=2J distinct voltage levels fs=Rd/J is the symbol rate (baud rate) Impulse modulator Represent the symbol sequence by the Dirac impulse train The impulse modulator block forms this function. This impulse train is applied to a transmit pulse shaping filter so that the signal is band limited to the channel bandwidth. 1 Pulse Shaping and PAM When the message signal is digital, it must be converted into an analog signal in order to be transmitted. “pulse shaping” filter changes the symbol into a suitable analog pulse Each symbol w(kT) initiates an analog pulse that is scaled by the value of the signal Pulse Shaping Compose the analog pulse train entering the pulse shaping filter as which is w(kT) for t = kT and 0 for t = kT Pulse shaping filter output 2 Pulse Shaping 4-PAM symbol sequence triggering baud-spaced rectangular pulse Intersymbol Interference If the analog pulse is wider than the time between adjacent symbols, the outputs from adjacent symbols may overlap A problem called intersymbol interference (ISI) What kind of pulses minimize the ISI? Choose a shape that is one at time kT and zero at mT for all m≠k Then, the analog waveform contains only the value from the desired input symbol and no interference from other nearby input symbols.
    [Show full text]
  • ENSC327 Communications Systems 25: ISI and Pulse Shaping (Ch 6)
    ENSC327 Communications Systems 25: ISI and Pulse Shaping (Ch 6) Jie Liang School of Engineering Science Simon Fraser University 1 Outline Chapter 6: Baseband Data Transmission No modulation, sending pulse sequences directly Suitable for lowpass channels (eg, coaxial cables) (Chap 7 will study digital bandpass modulation, f or bandpass channels (eg, wireless) that need high-freq carrier) ISI and Pulse Shaping ISI Definition Zero ISI Condition Nyquist Pulse Shaping Condition Nyquist bandwidth Nyquist channel 2 Introduction A digital communication system involves the following operations: Transmitter: maps the digital information to analog electromagnetic energy. Receiver: records the analog electromagnetic energy, and recover the digital information. The system can introduces two kinds of distortions: Channel noise: due to random and unpredictable physical phenomena. Studied in Chap. 9 and 10. Intersymbol interference (ISI) : due to imperfections in the frequency response of the channel. The main issues is that previously transmitted symbols affect the current received symbol. 3 Studied in Chap. 6. 6.1 Baseband Transmission with PAM Input : binary data, bk = 0 or 1, with duration Tb. Bit rate: 1/T b bits/second. Line encoder (Chap. 5): electrical representation of the binary sequences, e.g., + ,1 bk = ,1 ak = b − ,1 k = .0 4 6.1 Baseband Transmission with PAM Transmit filter : use pulses of different amplitudes to represent one or more binary bits. The basic shape is represented by a filter g(t) or G(f) The output discrete PAM signal from the transmitter: 5 6.1 Baseband Transmission with PAM Channel : If the channel is ideal, no distortion will be introduced.
    [Show full text]
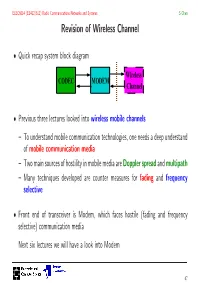
  • Revision of Wireless Channel
    ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Revision of Wireless Channel • Quick recap system block diagram Wireless CODEC MODEM Channel • Previous three lectures looked into wireless mobile channels – To understand mobile communication technologies, one needs a deep understand of mobile communication media – Two main sources of hostility in mobile media are Doppler spread and multipath – Many techniques developed are counter measures for fading and frequency selective • Front end of transceiver is Modem, which faces hostile (fading and frequency selective) communication media Next six lectures we will have a look into Modem 47 ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Digital Modulation Overview • Schematic of MODEM (modulation and demodulation) with its basic components: clock carrier pulse b(k) x(k) x(t) s(t) pulse Tx filter bits to modulat. symbols generator GT (f) clock carrier channel recovery recovery GC (f) ^ b(k) x(k)^x(t) ^s(t) ^ symbols sampler/ Rx filter AWGN demodul. + to bits decision GR (f) n(t) • The purpose of MODEM: transfer the bit stream at certain rate over the communication medium reliably 48 ELEC6014 (EZ412/612) Radio Communications Networks and Systems S Chen Constellation Diagram • Digital modulation signal has finite states. This manifests in symbol (message) set: M = {m1, m2, ··· , mM }, where each symbol contains log2 M bits • Or in modulation signal set: S = {s1(t),s2(t), ··· sM (t)}. There is one-to-one relationship between two sets: modulation scheme M
    [Show full text]
  • Digital Baseband Communication Systems for More Information: Read Chapters 1, 6 and 7 in Your Textbook Or Visit
    EE 421: Communications I Prof. Mohammed Hawa Introduction to Digital Baseband Communication Systems For more information: read Chapters 1, 6 and 7 in your textbook or visit http://wikipedia.org/. Remember that communication systems in general can be classified into four categories: Analog Baseband Systems, Analog Carrier Systems ( using analog modulation), Digital Baseband Systems and Digital Carrier Systems ( using digital modulation). Digital baseband and digital carrier transmission systems have many advantages over their analog counterparts. Some of these advantages are: 1. Digital transmission systems are more immune to noise due to threshold detection at the receiver; and the availability of regenerative repeaters, which can be used instead of analog amplifiers at intermediate points throughout the transmission channel. 2. Digital transmission systems allow multiplexing at both the baseband level (e.g., TDM) and carrier level (e.g., FDM, CDMA and OFDMA), which means we can easily carry multiple conversations (signals) on a single physical medium (channel). 3. The ability to use spread spectrum techniques in digital systems help overcome jamming and interference and allows us to hide the transmitted signal within noise if necessary. In addition, the use of orthogonality is easier and allows increasing the transmission rate by overcoming impairments such as fading. 4. The possibility of using channel coding techniques (i.e., error correcting codes) in digital communications reduces bit errors at the receiver (i.e., it effectively improves the signal-to-noise ratio (SNR)). 5. The possibility of using source coding techniques (i.e., compression) in digital communications reduces the amount of bits being transmitted, and hence, allows for more bandwidth efficiency.
    [Show full text]
  • Pulse Shaping and Matched Filtering
    LAB 4: PULSE SHAPING AND MATCHED FILTERING I. OVERVIEW The objective of this laboratory session is to introduce the basics of pulse shaping and matched filtering designs in digital communication systems. At the transmitter, we focus on pulse shaping; while at the receiver, we focus on matched filtering. Pulse shaping is the process of shaping pulses to be transmitted based on the symbols generated via modulation (Lab 3). The goal is to make the signal suitable to be transmitted through the communication channel mainly by limiting its effective bandwidth. In the first part of this lab, we build a pulse shaping virtual instrument (VI) that is capable of shaping pulses by lowpass filtering. In the second part, we build a matched filter to the pulse shape to maximize the signal to noise ratio before symbol detection. A general block diagram of a transmitter is given in Fig. 1 below: Fig. 1 – Transmitter block diagram A general block diagram of a receiver is given in Fig. 2 below: 1 Fig. 2 – Receiver block diagram In this lab session we implement the Pulse shaping part at the transmitter and the Matched filter part at the receiver. PART 1: PULSE SHAPING In communications, digital signals need to be mapped to an analog waveform in order to be transmitted over the channel. The mapping process is accomplished in two steps: (i) Mapping from source bits to complex symbols (also known as constellation points), which we learned about in Lab 3 – Part 1: Modulation. (ii) Mapping from complex symbols to analog pulse trains, which is studied in this part.
    [Show full text]