Euler's Formula and Trigonometry
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Integration in the Complex Plane (Zill & Wright Chapter
Integration in the Complex Plane (Zill & Wright Chapter 18) 1016-420-02: Complex Variables∗ Winter 2012-2013 Contents 1 Contour Integrals 2 1.1 Definition and Properties . 2 1.2 Evaluation . 3 1.2.1 Example: R z¯ dz ............................. 3 C1 1.2.2 Example: R z¯ dz ............................. 4 C2 R 2 1.2.3 Example: C z dz ............................. 4 1.3 The ML Limit . 5 1.4 Circulation and Flux . 5 2 The Cauchy-Goursat Theorem 7 2.1 Integral Around a Closed Loop . 7 2.2 Independence of Path for Analytic Functions . 8 2.3 Deformation of Closed Contours . 9 2.4 The Antiderivative . 10 3 Cauchy's Integral Formulas 12 3.1 Cauchy's Integral Formula . 12 3.1.1 Example #1 . 13 3.1.2 Example #2 . 13 3.2 Cauchy's Integral Formula for Derivatives . 14 3.3 Consequences of Cauchy's Integral Formulas . 16 3.3.1 Cauchy's Inequality . 16 3.3.2 Liouville's Theorem . 16 ∗Copyright 2013, John T. Whelan, and all that 1 Tuesday 18 December 2012 1 Contour Integrals 1.1 Definition and Properties Recall the definition of the definite integral Z xF X f(x) dx = lim f(xk) ∆xk (1.1) ∆xk!0 xI k We'd like to define a similar concept, integrating a function f(z) from some point zI to another point zF . The problem is that, since zI and zF are points in the complex plane, there are different ways to get between them, and adding up the value of the function along one path will not give the same result as doing it along another path, even if they have the same endpoints. -

Refresher Course Content
Calculus I Refresher Course Content 4. Exponential and Logarithmic Functions Section 4.1: Exponential Functions Section 4.2: Logarithmic Functions Section 4.3: Properties of Logarithms Section 4.4: Exponential and Logarithmic Equations Section 4.5: Exponential Growth and Decay; Modeling Data 5. Trigonometric Functions Section 5.1: Angles and Radian Measure Section 5.2: Right Triangle Trigonometry Section 5.3: Trigonometric Functions of Any Angle Section 5.4: Trigonometric Functions of Real Numbers; Periodic Functions Section 5.5: Graphs of Sine and Cosine Functions Section 5.6: Graphs of Other Trigonometric Functions Section 5.7: Inverse Trigonometric Functions Section 5.8: Applications of Trigonometric Functions 6. Analytic Trigonometry Section 6.1: Verifying Trigonometric Identities Section 6.2: Sum and Difference Formulas Section 6.3: Double-Angle, Power-Reducing, and Half-Angle Formulas Section 6.4: Product-to-Sum and Sum-to-Product Formulas Section 6.5: Trigonometric Equations 7. Additional Topics in Trigonometry Section 7.1: The Law of Sines Section 7.2: The Law of Cosines Section 7.3: Polar Coordinates Section 7.4: Graphs of Polar Equations Section 7.5: Complex Numbers in Polar Form; DeMoivre’s Theorem Section 7.6: Vectors Section 7.7: The Dot Product 8. Systems of Equations and Inequalities (partially included) Section 8.1: Systems of Linear Equations in Two Variables Section 8.2: Systems of Linear Equations in Three Variables Section 8.3: Partial Fractions Section 8.4: Systems of Nonlinear Equations in Two Variables Section 8.5: Systems of Inequalities Section 8.6: Linear Programming 10. Conic Sections and Analytic Geometry (partially included) Section 10.1: The Ellipse Section 10.2: The Hyperbola Section 10.3: The Parabola Section 10.4: Rotation of Axes Section 10.5: Parametric Equations Section 10.6: Conic Sections in Polar Coordinates 11. -
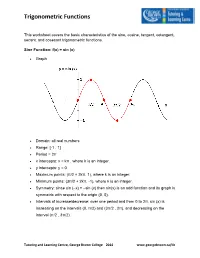
Trigonometric Functions
Trigonometric Functions This worksheet covers the basic characteristics of the sine, cosine, tangent, cotangent, secant, and cosecant trigonometric functions. Sine Function: f(x) = sin (x) • Graph • Domain: all real numbers • Range: [-1 , 1] • Period = 2π • x intercepts: x = kπ , where k is an integer. • y intercepts: y = 0 • Maximum points: (π/2 + 2kπ, 1), where k is an integer. • Minimum points: (3π/2 + 2kπ, -1), where k is an integer. • Symmetry: since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0). • Intervals of increase/decrease: over one period and from 0 to 2π, sin (x) is increasing on the intervals (0, π/2) and (3π/2 , 2π), and decreasing on the interval (π/2 , 3π/2). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Cosine Function: f(x) = cos (x) • Graph • Domain: all real numbers • Range: [–1 , 1] • Period = 2π • x intercepts: x = π/2 + k π , where k is an integer. • y intercepts: y = 1 • Maximum points: (2 k π , 1) , where k is an integer. • Minimum points: (π + 2 k π , –1) , where k is an integer. • Symmetry: since cos(–x) = cos(x) then cos (x) is an even function and its graph is symmetric with respect to the y axis. • Intervals of increase/decrease: over one period and from 0 to 2π, cos (x) is decreasing on (0 , π) increasing on (π , 2π). Tutoring and Learning Centre, George Brown College 2014 www.georgebrown.ca/tlc Trigonometric Functions Tangent Function : f(x) = tan (x) • Graph • Domain: all real numbers except π/2 + k π, k is an integer. -

Lecture 5: Complex Logarithm and Trigonometric Functions
LECTURE 5: COMPLEX LOGARITHM AND TRIGONOMETRIC FUNCTIONS Let C∗ = C \{0}. Recall that exp : C → C∗ is surjective (onto), that is, given w ∈ C∗ with w = ρ(cos φ + i sin φ), ρ = |w|, φ = Arg w we have ez = w where z = ln ρ + iφ (ln stands for the real log) Since exponential is not injective (one one) it does not make sense to talk about the inverse of this function. However, we also know that exp : H → C∗ is bijective. So, what is the inverse of this function? Well, that is the logarithm. We start with a general definition Definition 1. For z ∈ C∗ we define log z = ln |z| + i argz. Here ln |z| stands for the real logarithm of |z|. Since argz = Argz + 2kπ, k ∈ Z it follows that log z is not well defined as a function (it is multivalued), which is something we find difficult to handle. It is time for another definition. Definition 2. For z ∈ C∗ the principal value of the logarithm is defined as Log z = ln |z| + i Argz. Thus the connection between the two definitions is Log z + 2kπ = log z for some k ∈ Z. Also note that Log : C∗ → H is well defined (now it is single valued). Remark: We have the following observations to make, (1) If z 6= 0 then eLog z = eln |z|+i Argz = z (What about Log (ez)?). (2) Suppose x is a positive real number then Log x = ln x + i Argx = ln x (for positive real numbers we do not get anything new). -

1 the Complex Plane
Math 135A, Winter 2012 Complex numbers 1 The complex numbers C are important in just about every branch of mathematics. These notes present some basic facts about them. 1 The Complex Plane A complex number z is given by a pair of real numbers x and y and is written in the form z = x+iy, where i satisfies i2 = −1. The complex numbers may be represented as points in the plane, with the real number 1 represented by the point (1; 0), and the complex number i represented by the point (0; 1). The x-axis is called the \real axis," and the y-axis is called the \imaginary axis." For example, the complex numbers 1, i, 3 + 4i and 3 − 4i are illustrated in Fig 1a. 3 + 4i 6 + 4i 2 + 3i imag i 4 + i 1 real 3 − 4i Fig 1a Fig 1b Complex numbers are added in a natural way: If z1 = x1 + iy1 and z2 = x2 + iy2, then z1 + z2 = (x1 + x2) + i(y1 + y2) (1) It's just vector addition. Fig 1b illustrates the addition (4 + i) + (2 + 3i) = (6 + 4i). Multiplication is given by z1z2 = (x1x2 − y1y2) + i(x1y2 + x2y1) Note that the product behaves exactly like the product of any two algebraic expressions, keeping in mind that i2 = −1. Thus, (2 + i)(−2 + 4i) = 2(−2) + 8i − 2i + 4i2 = −8 + 6i We call x the real part of z and y the imaginary part, and we write x = Re z, y = Im z.(Remember: Im z is a real number.) The term \imaginary" is a historical holdover; it took mathematicians some time to accept the fact that i (for \imaginary," naturally) was a perfectly good mathematical object. -

An Appreciation of Euler's Formula
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 1 Article 17 An Appreciation of Euler's Formula Caleb Larson North Dakota State University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Larson, Caleb (2017) "An Appreciation of Euler's Formula," Rose-Hulman Undergraduate Mathematics Journal: Vol. 18 : Iss. 1 , Article 17. Available at: https://scholar.rose-hulman.edu/rhumj/vol18/iss1/17 Rose- Hulman Undergraduate Mathematics Journal an appreciation of euler's formula Caleb Larson a Volume 18, No. 1, Spring 2017 Sponsored by Rose-Hulman Institute of Technology Department of Mathematics Terre Haute, IN 47803 [email protected] a scholar.rose-hulman.edu/rhumj North Dakota State University Rose-Hulman Undergraduate Mathematics Journal Volume 18, No. 1, Spring 2017 an appreciation of euler's formula Caleb Larson Abstract. For many mathematicians, a certain characteristic about an area of mathematics will lure him/her to study that area further. That characteristic might be an interesting conclusion, an intricate implication, or an appreciation of the impact that the area has upon mathematics. The particular area that we will be exploring is Euler's Formula, eix = cos x + i sin x, and as a result, Euler's Identity, eiπ + 1 = 0. Throughout this paper, we will develop an appreciation for Euler's Formula as it combines the seemingly unrelated exponential functions, imaginary numbers, and trigonometric functions into a single formula. To appreciate and further understand Euler's Formula, we will give attention to the individual aspects of the formula, and develop the necessary tools to prove it. -

Appendix B. Random Number Tables
Appendix B. Random Number Tables Reproduced from Million Random Digits, used with permission of the Rand Corporation, Copyright, 1955, The Free Press. The publication is available for free on the Internet at http://www.rand.org/publications/classics/randomdigits. All of the sampling plans presented in this handbook are based on the assumption that the packages constituting the sample are chosen at random from the inspection lot. Randomness in this instance means that every package in the lot has an equal chance of being selected as part of the sample. It does not matter what other packages have already been chosen, what the package net contents are, or where the package is located in the lot. To obtain a random sample, two steps are necessary. First it is necessary to identify each package in the lot of packages with a specific number whether on the shelf, in the warehouse, or coming off the packaging line. Then it is necessary to obtain a series of random numbers. These random numbers indicate exactly which packages in the lot shall be taken for the sample. The Random Number Table The random number tables in Appendix B are composed of the digits from 0 through 9, with approximately equal frequency of occurrence. This appendix consists of 8 pages. On each page digits are printed in blocks of five columns and blocks of five rows. The printing of the table in blocks is intended only to make it easier to locate specific columns and rows. Random Starting Place Starting Page. The Random Digit pages numbered B-2 through B-8. -
The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs in first Year Calculus You Learned About the Formula: Z B 1 Dx = Ln |B| − Ln |A| a X
The Integral Resulting in a Logarithm of a Complex Number Dr. E. Jacobs In first year calculus you learned about the formula: Z b 1 dx = ln jbj ¡ ln jaj a x It is natural to want to apply this formula to contour integrals. If z1 and z2 are complex numbers and C is a path connecting z1 to z2, we would expect that: Z 1 dz = log z2 ¡ log z1 C z However, you are about to see that there is an interesting complication when we take the formula for the integral resulting in logarithm and try to extend it to the complex case. First of all, recall that if f(z) is an analytic function on a domain D and C is a closed loop in D then : I f(z) dz = 0 This is referred to as the Cauchy-Integral Theorem. So, for example, if C His a circle of radius r around the origin we may conclude immediately that 2 2 C z dz = 0 because z is an analytic function for all values of z. H If f(z) is not analytic then C f(z) dz is not necessarily zero. Let’s do an 1 explicit calculation for f(z) = z . If we are integrating around a circle C centered at the origin, then any point z on this path may be written as: z = reiθ H 1 iθ Let’s use this to integrate C z dz. If z = re then dz = ireiθ dθ H 1 Now, substitute this into the integral C z dz. -

Effects of a Prescribed Fire on Oak Woodland Stand Structure1
Effects of a Prescribed Fire on Oak Woodland Stand Structure1 Danny L. Fry2 Abstract Fire damage and tree characteristics of mixed deciduous oak woodlands were recorded after a prescription burn in the summer of 1999 on Mt. Hamilton Range, Santa Clara County, California. Trees were tagged and monitored to determine the effects of fire intensity on damage, recovery and survivorship. Fire-caused mortality was low; 2-year post-burn survey indicates that only three oaks have died from the low intensity ground fire. Using ANOVA, there was an overall significant difference for percent tree crown scorched and bole char height between plots, but not between tree-size classes. Using logistic regression, tree diameter and aspect predicted crown resprouting. Crown damage was also a significant predictor of resprouting with the likelihood increasing with percent scorched. Both valley and blue oaks produced crown resprouts on trees with 100 percent of their crown scorched. Although overall tree damage was low, crown resprouts developed on 80 percent of the trees and were found as shortly as two weeks after the fire. Stand structural characteristics have not been altered substantially by the event. Long term monitoring of fire effects will provide information on what changes fire causes to stand structure, its possible usefulness as a management tool, and how it should be applied to the landscape to achieve management objectives. Introduction Numerous studies have focused on the effects of human land use practices on oak woodland stand structure and regeneration. Studies examining stand structure in oak woodlands have shown either persistence or strong recruitment following fire (McClaran and Bartolome 1989, Mensing 1992). -

Complex Sinusoids Copyright C Barry Van Veen 2014
Complex Sinusoids Copyright c Barry Van Veen 2014 Feel free to pass this ebook around the web... but please do not modify any of its contents. Thanks! AllSignalProcessing.com Key Concepts 1) The real part of a complex sinusoid is a cosine wave and the imag- inary part is a sine wave. 2) A complex sinusoid x(t) = AejΩt+φ can be visualized in the complex plane as a vector of length A that is rotating at a rate of Ω radians per second and has angle φ relative to the real axis at time t = 0. a) The projection of the complex sinusoid onto the real axis is the cosine A cos(Ωt + φ). b) The projection of the complex sinusoid onto the imaginary axis is the cosine A sin(Ωt + φ). AllSignalProcessing.com 3) The output of a linear time invariant system in response to a com- plex sinusoid input is a complex sinusoid of the of the same fre- quency. The system only changes the amplitude and phase of the input complex sinusoid. a) Arbitrary input signals are represented as weighted sums of complex sinusoids of different frequencies. b) Then, the output is a weighted sum of complex sinusoids where the weights have been multiplied by the complex gain of the system. 4) Complex sinusoids also simplify algebraic manipulations. AllSignalProcessing.com 5) Real sinusoids can be expressed as a sum of a positive and negative frequency complex sinusoid. 6) The concept of negative frequency is not physically meaningful for real data and is an artifact of using complex sinusoids. -

Lesson 6: Trigonometric Identities
1. Introduction An identity is an equality relationship between two mathematical expressions. For example, in basic algebra students are expected to master various algbriac factoring identities such as a2 − b2 =(a − b)(a + b)or a3 + b3 =(a + b)(a2 − ab + b2): Identities such as these are used to simplifly algebriac expressions and to solve alge- a3 + b3 briac equations. For example, using the third identity above, the expression a + b simpliflies to a2 − ab + b2: The first identiy verifies that the equation (a2 − b2)=0is true precisely when a = b: The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry. Such identities can be used to simplifly complicated trigonometric expressions. This lesson contains several examples and exercises to demonstrate this type of procedure. Trigonometric identities can also used solve trigonometric equations. Equations of this type are introduced in this lesson and examined in more detail in Lesson 7. For student’s convenience, the identities presented in this lesson are sumarized in Appendix A 2. The Elementary Identities Let (x; y) be the point on the unit circle centered at (0; 0) that determines the angle t rad : Recall that the definitions of the trigonometric functions for this angle are sin t = y tan t = y sec t = 1 x y : cos t = x cot t = x csc t = 1 y x These definitions readily establish the first of the elementary or fundamental identities given in the table below. For obvious reasons these are often referred to as the reciprocal and quotient identities. -

CHAPTER 8. COMPLEX NUMBERS Why Do We Need Complex Numbers? First of All, a Simple Algebraic Equation Like X2 = −1 May Not Have
CHAPTER 8. COMPLEX NUMBERS Why do we need complex numbers? First of all, a simple algebraic equation like x2 = 1 may not have a real solution. − Introducing complex numbers validates the so called fundamental theorem of algebra: every polynomial with a positive degree has a root. However, the usefulness of complex numbers is much beyond such simple applications. Nowadays, complex numbers and complex functions have been developed into a rich theory called complex analysis and be- come a power tool for answering many extremely difficult questions in mathematics and theoretical physics, and also finds its usefulness in many areas of engineering and com- munication technology. For example, a famous result called the prime number theorem, which was conjectured by Gauss in 1849, and defied efforts of many great mathematicians, was finally proven by Hadamard and de la Vall´ee Poussin in 1896 by using the complex theory developed at that time. A widely quoted statement by Jacques Hadamard says: “The shortest path between two truths in the real domain passes through the complex domain”. The basic idea for complex numbers is to introduce a symbol i, called the imaginary unit, which satisfies i2 = 1. − In doing so, x2 = 1 turns out to have a solution, namely x = i; (actually, there − is another solution, namely x = i). We remark that, sometimes in the mathematical − literature, for convenience or merely following tradition, an incorrect expression with correct understanding is used, such as writing √ 1 for i so that we can reserve the − letter i for other purposes. But we try to avoid incorrect usage as much as possible.