Additive Combinatorics and Its Applications in Theoretical Computer Science
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HKUST Newsletter-Genesis
World’s first smart coating - NEWSLETTER GENESIS to fight infectious diseases Issue 8 2O1O 全球首創智能塗層 有效控制傳染病 Aeronautics guru lands on HKUST – New Provost Prof Wei Shyy 航天專家科大著陸- 新首席副校長史維教授 Welcome 3-3-4 迎接三三四 目錄 C ontents President’s Message 校長的話 Physics professor awarded Croucher Fellowship 22 物理學系教授榮膺裘槎基金會優秀科研者 President’s Message 2 校長的話 Prof Wang Wenxiong of Biology awarded 23 First Class Prize by China’s Ministry of Education 生物系王文雄教授獲國家教育部優秀成果獎 Eureka! - Our Search & Research 一等獎 雄雞鳴 天下白―科研成果 香港―我們的家 HKUST develops world’s first smart anti-microbial Local 4 coating to control infectious diseases 科大研發全球首創智能殺菌塗層 有效控制傳染病 We are ready for 3-3-4 24 科大為迎接「三三四」作好準備 An out of this world solution to the 8 energy crisis: The moon holds the answer Legendary gymnast Dr Li Ning 月球的清潔能源可望解決地球能源危機 27 shares his dream at HKUST 與李寧博士對談:成功源自一個夢想 HKUST achieves breakthrough in wireless 10 technology to facilitate network traffic Chow Tai Fook Cheng Yu Tung Fund 科大無線通訊突破 有效管理網絡交通 28 donates $90 million to HKUST 科大喜獲周大福鄭裕彤基金捐贈九千萬元 HKUST develops hair-based drug testing 12 科大頭髮驗毒提供快而準的測試 CN Innovations Ltd donates $5 million 30 to HKUST to support applied research 中南創發有限公司捐贈五百萬元 The answer is in the genes: HKUST joins high- 助科大發展應用研究 14 powered global team to decode cancer genome 科大參與國際聯盟破解癌症基因 Honorary Fellowship Presentation Ceremony - 31 trio honored for dual achievement: doing good Raising the Bar 又上一層樓 while doing well 科大頒授榮譽院士 表揚社會貢獻 Celebrating our students’ outstanding 16 achievements 學生獲著名大學研究院錄取 師生同慶 National 祖國―我們的根 HKUST puts on great performance -

Advances in Pure Mathematics Special Issue on Number Theory
Advances in Pure Mathematics Scientific Research Open Access ISSN Online: 2160-0384 Special Issue on Number Theory Call for Papers Number theory (arithmetic) is devoted primarily to the study of the integers. It is sometimes called "The Queen of Mathematics" because of its foundational place in the discipline. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers). In this special issue, we intend to invite front-line researchers and authors to submit original research and review articles on number theory. Potential topics include, but are not limited to: Elementary tools Analytic number theory Algebraic number theory Diophantine geometry Probabilistic number theory Arithmetic combinatorics Computational number theory Applications Authors should read over the journal’s For Authors carefully before submission. Prospective authors should submit an electronic copy of their complete manuscript through the journal’s Paper Submission System. Please kindly notice that the “Special Issue” under your manuscript title is supposed to be specified and the research field “Special Issue – Number Theory” should be chosen during your submission. According to the following timetable: Submission Deadline November 2nd, 2020 Publication Date January 2021 For publishing inquiries, please feel free to contact the Editorial Assistant at [email protected] APM Editorial Office Home | About SCIRP | Sitemap | Contact Us Copyright © 2006-2020 Scientific Research Publishing Inc. All rights reserved. Advances in Pure Mathematics Scientific Research Open Access ISSN Online: 2160-0384 [email protected] Home | About SCIRP | Sitemap | Contact Us Copyright © 2006-2020 Scientific Research Publishing Inc. -

FUNDAMENTALS of COMPUTING (2019-20) COURSE CODE: 5023 502800CH (Grade 7 for ½ High School Credit) 502900CH (Grade 8 for ½ High School Credit)
EXPLORING COMPUTER SCIENCE NEW NAME: FUNDAMENTALS OF COMPUTING (2019-20) COURSE CODE: 5023 502800CH (grade 7 for ½ high school credit) 502900CH (grade 8 for ½ high school credit) COURSE DESCRIPTION: Fundamentals of Computing is designed to introduce students to the field of computer science through an exploration of engaging and accessible topics. Through creativity and innovation, students will use critical thinking and problem solving skills to implement projects that are relevant to students’ lives. They will create a variety of computing artifacts while collaborating in teams. Students will gain a fundamental understanding of the history and operation of computers, programming, and web design. Students will also be introduced to computing careers and will examine societal and ethical issues of computing. OBJECTIVE: Given the necessary equipment, software, supplies, and facilities, the student will be able to successfully complete the following core standards for courses that grant one unit of credit. RECOMMENDED GRADE LEVELS: 9-12 (Preference 9-10) COURSE CREDIT: 1 unit (120 hours) COMPUTER REQUIREMENTS: One computer per student with Internet access RESOURCES: See attached Resource List A. SAFETY Effective professionals know the academic subject matter, including safety as required for proficiency within their area. They will use this knowledge as needed in their role. The following accountability criteria are considered essential for students in any program of study. 1. Review school safety policies and procedures. 2. Review classroom safety rules and procedures. 3. Review safety procedures for using equipment in the classroom. 4. Identify major causes of work-related accidents in office environments. 5. Demonstrate safety skills in an office/work environment. -

Ergodic Theory and Combinatorial Number Theory
Mathematisches Forschungsinstitut Oberwolfach Report No. 50/2012 DOI: 10.4171/OWR/2012/50 Arbeitsgemeinschaft: Ergodic Theory and Combinatorial Number Theory Organised by Vitaly Bergelson, Columbus Nikos Frantzikinakis, Heraklion Terence Tao, Los Angeles Tamar Ziegler, Haifa 7th October – 13th October 2012 Abstract. The aim of this Arbeitsgemeinschaft was to introduce young re- searchers with various backgrounds to the multifaceted and mutually perpet- uating connections between ergodic theory, topological dynamics, combina- torics, and number theory. Mathematics Subject Classification (2000): 05D10, 11K06, 11B25, 11B30, 27A45, 28D05, 28D15, 37A30, 37A45, 37B05. Introduction by the Organisers In 1977 Furstenberg gave an ergodic proof of the celebrated theorem of Sze- mer´edi on arithmetic progressions, hereby starting a new field, ergodic Ramsey theory. Over the years the methods of ergodic theory and topological dynamics have led to very impressive developments in the fields of arithmetic combinatorics and Ramsey theory. Furstenberg’s original approach has been enhanced with sev- eral deep structural results of measure preserving systems, equidistribution results on nilmanifolds, the use of ultrafilters etc. Several novel techniques have been de- veloped and opened new vistas that led to new deep results, including far reaching extensions of Szemer´edi’s theorem, results in Euclidean Ramsey theory, multiple recurrence results for non-abelian group actions, convergence results for multiple ergodic averages etc. These methods have also facilitated the recent spectacu- lar progress on patterns in primes. The field of ergodic theory has tremendously benefited, since the problems of combinatorial and number-theoretic nature have given a boost to the in depth study of recurrence and convergence problems. -

Number Theory
“mcs-ftl” — 2010/9/8 — 0:40 — page 81 — #87 4 Number Theory Number theory is the study of the integers. Why anyone would want to study the integers is not immediately obvious. First of all, what’s to know? There’s 0, there’s 1, 2, 3, and so on, and, oh yeah, -1, -2, . Which one don’t you understand? Sec- ond, what practical value is there in it? The mathematician G. H. Hardy expressed pleasure in its impracticality when he wrote: [Number theorists] may be justified in rejoicing that there is one sci- ence, at any rate, and that their own, whose very remoteness from or- dinary human activities should keep it gentle and clean. Hardy was specially concerned that number theory not be used in warfare; he was a pacifist. You may applaud his sentiments, but he got it wrong: Number Theory underlies modern cryptography, which is what makes secure online communication possible. Secure communication is of course crucial in war—which may leave poor Hardy spinning in his grave. It’s also central to online commerce. Every time you buy a book from Amazon, check your grades on WebSIS, or use a PayPal account, you are relying on number theoretic algorithms. Number theory also provides an excellent environment for us to practice and apply the proof techniques that we developed in Chapters 2 and 3. Since we’ll be focusing on properties of the integers, we’ll adopt the default convention in this chapter that variables range over the set of integers, Z. 4.1 Divisibility The nature of number theory emerges as soon as we consider the divides relation a divides b iff ak b for some k: D The notation, a b, is an abbreviation for “a divides b.” If a b, then we also j j say that b is a multiple of a. -
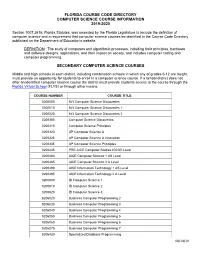
Florida Course Code Directory Computer Science Course Information 2019-2020
FLORIDA COURSE CODE DIRECTORY COMPUTER SCIENCE COURSE INFORMATION 2019-2020 Section 1007.2616, Florida Statutes, was amended by the Florida Legislature to include the definition of computer science and a requirement that computer science courses be identified in the Course Code Directory published on the Department of Education’s website. DEFINITION: The study of computers and algorithmic processes, including their principles, hardware and software designs, applications, and their impact on society, and includes computer coding and computer programming. SECONDARY COMPUTER SCIENCE COURSES Middle and high schools in each district, including combination schools in which any of grades 6-12 are taught, must provide an opportunity for students to enroll in a computer science course. If a school district does not offer an identified computer science course the district must provide students access to the course through the Florida Virtual School (FLVS) or through other means. COURSE NUMBER COURSE TITLE 0200000 M/J Computer Science Discoveries 0200010 M/J Computer Science Discoveries 1 0200020 M/J Computer Science Discoveries 2 0200305 Computer Science Discoveries 0200315 Computer Science Principles 0200320 AP Computer Science A 0200325 AP Computer Science A Innovation 0200335 AP Computer Science Principles 0200435 PRE-AICE Computer Studies IGCSE Level 0200480 AICE Computer Science 1 AS Level 0200485 AICE Computer Science 2 A Level 0200490 AICE Information Technology 1 AS Level 0200495 AICE Information Technology 2 A Level 0200800 IB Computer -

FROM HARMONIC ANALYSIS to ARITHMETIC COMBINATORICS: a BRIEF SURVEY the Purpose of This Note Is to Showcase a Certain Line Of
FROM HARMONIC ANALYSIS TO ARITHMETIC COMBINATORICS: A BRIEF SURVEY IZABELLA ÃLABA The purpose of this note is to showcase a certain line of research that connects harmonic analysis, speci¯cally restriction theory, to other areas of mathematics such as PDE, geometric measure theory, combinatorics, and number theory. There are many excellent in-depth presentations of the vari- ous areas of research that we will discuss; see e.g., the references below. The emphasis here will be on highlighting the connections between these areas. Our starting point will be restriction theory in harmonic analysis on Eu- clidean spaces. The main theme of restriction theory, in this context, is the connection between the decay at in¯nity of the Fourier transforms of singu- lar measures and the geometric properties of their support, including (but not necessarily limited to) curvature and dimensionality. For example, the Fourier transform of a measure supported on a hypersurface in Rd need not, in general, belong to any Lp with p < 1, but there are positive results if the hypersurface in question is curved. A classic example is the restriction theory for the sphere, where a conjecture due to E. M. Stein asserts that the Fourier transform maps L1(Sd¡1) to Lq(Rd) for all q > 2d=(d¡1). This has been proved in dimension 2 (Fe®erman-Stein, 1970), but remains open oth- erwise, despite the impressive and often groundbreaking work of Bourgain, Wol®, Tao, Christ, and others. We recommend [8] for a thorough survey of restriction theory for the sphere and other curved hypersurfaces. Restriction-type estimates have been immensely useful in PDE theory; in fact, much of the interest in the subject stems from PDE applications. -

Green-Tao Theorem in Function Fields 11
GREEN-TAO THEOREM IN FUNCTION FIELDS THAI´ HOANG` LE^ Abstract. We adapt the proof of the Green-Tao theorem on arithmetic progressions in primes to the setting of polynomials over a finite fields, to show that for every k, the irreducible polynomials in Fq[t] contains configurations of the form ff + P g : deg(P ) < kg; g 6= 0. 1. Introduction In [13], Green and Tao proved the following celebrated theorem now bearing their name: Theorem 1 (Green-Tao). The primes contain arithmetic progressions of arbitrarily length. Furthermore, the same conclusion is true for any subset of positive relative upper density of the primes. Subsequently, other variants of this theorem have been proved. Tao and Ziegler [26] proved the generalization for polynomial progressions a + p1(d); : : : ; a + pk(d), where pi 2 Z[x] and pi(0) = 0. Tao [24] proved the analog in the Gaussian integers. It is well known that the integers and the polynomials over a finite field share a lot of similarities in many aspects relevant to arithmetic combinatorics. Therefore, it is natural, as Green and Tao did, to suggest that the analog of this theorem should hold in the setting of function fields: Conjecture 1. For any finite field F, the monic irreducible polynomials in F[t] contain affine spaces of arbitrarily high dimension. We give an affirmative answer to this conjecture. More precisely, we will prove: Theorem 2 (Green-Tao for function fields). Let Fq be a finite field over q elements. Then for any k > 0, we can find polynomials f; g 2 Fq[t]; g 6= 0 such that the polynomials f + P g, where P runs over all polynomials P 2 Fq[t] of degree less than k, are all irreducible. -

Safety and Security Challenge
SAFETY AND SECURITY CHALLENGE TOP SUPERCOMPUTERS IN THE WORLD - FEATURING TWO of DOE’S!! Summary: The U.S. Department of Energy (DOE) plays a very special role in In fields where scientists deal with issues from disaster relief to the keeping you safe. DOE has two supercomputers in the top ten supercomputers in electric grid, simulations provide real-time situational awareness to the whole world. Titan is the name of the supercomputer at the Oak Ridge inform decisions. DOE supercomputers have helped the Federal National Laboratory (ORNL) in Oak Ridge, Tennessee. Sequoia is the name of Bureau of Investigation find criminals, and the Department of the supercomputer at Lawrence Livermore National Laboratory (LLNL) in Defense assess terrorist threats. Currently, ORNL is building a Livermore, California. How do supercomputers keep us safe and what makes computing infrastructure to help the Centers for Medicare and them in the Top Ten in the world? Medicaid Services combat fraud. An important focus lab-wide is managing the tsunamis of data generated by supercomputers and facilities like ORNL’s Spallation Neutron Source. In terms of national security, ORNL plays an important role in national and global security due to its expertise in advanced materials, nuclear science, supercomputing and other scientific specialties. Discovery and innovation in these areas are essential for protecting US citizens and advancing national and global security priorities. Titan Supercomputer at Oak Ridge National Laboratory Background: ORNL is using computing to tackle national challenges such as safe nuclear energy systems and running simulations for lower costs for vehicle Lawrence Livermore's Sequoia ranked No. -

Pure Mathematics
Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture. -

From Arithmetic to Algebra
From arithmetic to algebra Slightly edited version of a presentation at the University of Oregon, Eugene, OR February 20, 2009 H. Wu Why can’t our students achieve introductory algebra? This presentation specifically addresses only introductory alge- bra, which refers roughly to what is called Algebra I in the usual curriculum. Its main focus is on all students’ access to the truly basic part of algebra that an average citizen needs in the high- tech age. The content of the traditional Algebra II course is on the whole more technical and is designed for future STEM students. In place of Algebra II, future non-STEM would benefit more from a mathematics-culture course devoted, for example, to an understanding of probability and data, recently solved famous problems in mathematics, and history of mathematics. At least three reasons for students’ failure: (A) Arithmetic is about computation of specific numbers. Algebra is about what is true in general for all numbers, all whole numbers, all integers, etc. Going from the specific to the general is a giant conceptual leap. Students are not prepared by our curriculum for this leap. (B) They don’t get the foundational skills needed for algebra. (C) They are taught incorrect mathematics in algebra classes. Garbage in, garbage out. These are not independent statements. They are inter-related. Consider (A) and (B): The K–3 school math curriculum is mainly exploratory, and will be ignored in this presentation for simplicity. Grades 5–7 directly prepare students for algebra. Will focus on these grades. Here, abstract mathematics appears in the form of fractions, geometry, and especially negative fractions. -

A Logical Approach to Asymptotic Combinatorics I. First Order Properties
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector ADVANCES IN MATI-EMATlCS 65, 65-96 (1987) A Logical Approach to Asymptotic Combinatorics I. First Order Properties KEVIN J. COMPTON ’ Wesleyan University, Middletown, Connecticut 06457 INTRODUCTION We shall present a general framework for dealing with an extensive set of problems from asymptotic combinatorics; this framework provides methods for determining the probability that a large, finite structure, ran- domly chosen from a given class, will have a given property. Our main concern is the asymptotic probability: the limiting value as the size of the structure increases. For example, a common problem in elementary probability texts is to show that the asymptotic probabity that a per- mutation will have no fixed point is l/e. We shall say nothing about the closely related problem of determining rates of convergence, although the methods presented here may extend to such problems. To develop a general approach we must fix a language for specifying properties of structures. Thus, our approach is logical; logic is the branch of mathematics that deals with problems of language. In this paper we con- sider properties expressible in the language of first order logic and speak of probabilities of first order sentences rather than properties. In the sequel to this paper we consider properties expressible in the more general language of monadic second order logic. Clearly, we must restrict the classes of structures we consider in order for questions about asymptotic probabilities to be meaningful and significant. Therefore, we choose to consider only classes closed under disjoint unions and components (see Sect.