Regression Analyses of Migration with an Application to Selected Provinces in Thailand
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Eastern Seaboard Report
Eastern Seaboard Report October 2014 – Prepared by Mark Bowling, Chairman ESB Thailand's bearish automotive market has deterred two Japanese car makers, Mitsubishi Motors Corporation and Nissan Motor, from commencing production of their new eco- car. "Our parent company has not yet approved the exact time frame for production, as the domestic market has experienced weaker growth than was enjoyed in 2012," said Masahiko Ueki, president and chief executive of Mitsubishi Motors (Thailand). "Next year's prospects are unpredictable, as the economy and consumption will take time to recover," he said. Mitsubishi was one of the five companies that applied for Board of Investment (BoI) promotion for the second phase of the eco-car scheme. All eco-car production will be done at Mitsubishi's third plant in Laem Chabang Industrial Estate in Chon Buri province. The government confirmed changes to its high-speed development plan, adding a Bangkok-Rayong route and splitting the Nong Khai-Map Ta Phut route into two — Nong Khai-Nakhon Ratchasima and Nakhon Ratchasima-Bangkok-Map Ta Phut. The Nong Khai- Map Ta Phut route would cover 737 kilometres and cost 393 billion baht, while the Chiang Khong-Phachi route would be 655 km and cost 349 billion. Two high-speed rail routes costing a combined 741 billion baht would link Thailand with southern China. Bang Na-Trat office demand up - With office rents in Bangkok's central business district rising by 15% last year and nearly 6% more so far this year, more companies are considering Bang Na-Trat Road an alternative due to its competitive rents and convenient access to both the CBD and the Eastern Seaboard. -

Creating Curriculum of English for Conservative Tourism for Junior Guides to Promote Tourist Attractions in Thailand
English Language Teaching; Vol. 11, No. 3; 2018 ISSN 1916-4742 E-ISSN 1916-4750 Published by Canadian Center of Science and Education Creating Curriculum of English for Conservative Tourism for Junior Guides to Promote Tourist Attractions in Thailand Onsiri Wimontham1 1 English Education Curriculum, Nakhon Ratchasima Rajabhat University, Thailand Correspondence: Onsiri Wimontham, English Education Curriculum, Nakhon Ratchasima Rajabhat University, Thailand. E-mail: [email protected] Received: January 1, 2018 Accepted: February 13, 2018 Online Published: February 15, 2018 doi: 10.5539/elt.v11n3p67 URL: http://doi.org/10.5539/elt.v11n3p67 Abstract This research was supported the research fund of 2017 by Office of the Higher Education Commission of Thailand. The objectives of this research are listed below. 1). To form the model of teaching and learning English for local development by English curriculum (B. Ed.) students’ participation in training on out-of-classroom learning management, which focuses on the students’ English skills improvement along with developing the sense of love of their home towns. 2). To create curriculum of English training for conservative tourism for junior guides in Sung Noen District, Nakhon Ratchasima Province. 3). To promote conservative tourist attractions in Sung Noen District, Nakhon Ratchasima Province among foreign tourists, and to boost the local economy so that young generations can earn income and rely on themselves in the future. An interesting result from the research was more income gained from tourism in Sung Noen District, Nakhon Ratchasima Province between April 2016 and June in the same year. The junior guides’ ability to communicate and provide information about tourism in English was evaluated. -

Factors Associated with Quality of Life in the Elderly People with Ability in Sung Noen District, Nakhon Ratchasima Province
Review of Integrative Business and Economics Research, Vol. 6, NRRU special issue 238 Factors Associated with Quality of Life in the Elderly People with Ability in Sung Noen District, Nakhon Ratchasima Province Tanida Phatisena Varaporn Chatpahol Faculty of Public health, Nakhon Ratchasima Rajabhat University, Nakhon Ratchasima,Thailand ABSTRACT This objectives of this cross-sectional analytical research were to study the level of the quality of life and factors associated with quality of life in the elderly people with ability in Sung Noen distric, Nakhon Ratchasima province. The sample group consisted of 334 elderly people which selected by using multistage random sampling. Data collection was done by interview forms based upon the quality of life indicators by the WHO (WHOQOL_BREF_THAI) include 20 items within 4 components. The data was analysed by using percentage, mean, standard deviation and correlation tests: chi-square. The findings showed that overall the quality of life in the elderly people with ability was at a good level. Three components of physical domain, social relationships and the environment were rated at good level. A component of psychological domain was rated at a fair level. There was associations at 95% level of significance between the quality of life and health problems. Recommendation from this study was to the related organization should develop the quality of life of the elderly by promoting mental health and caring their own health care. Keywords : Quality of Life, Elderly, Ability 1. INTRODUCTION Thailand is currently facing an aging society resulting from change in population structure with the decrease in birth and death rate. This phenomena stem from the social and economic development in the previous decades bringing high technology in medicine and public health service, thus, expending the age of people. -

An Inventory and Assessment of National Urban Mobility in Thailand
Development of a National Urban Mobility Programme - an Inventory and Assessment of National Urban Mobility in Thailand A project of the Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) in collaboration with the Thai Office of Transport and Traffic Policy and Planning (OTP) Final Report November 2019 Development of a National Urban Mobility Programme Project Background Transport is the highest energy-consuming sector in 40% of all countries worldwide, and causes about a quarter of energy-related CO2 emissions. To limit global warming to two degrees, an extensive transformation and decarbonisation of transport is necessary. The TRANSfer project’s objective is to increase the efforts of developing countries and emerging economies for climate-friendly transport. The project acts as a mitigation action preparation facility and thus, specifically supports the implementation of the Nationally Determined Contributions (NDC) of the Paris Agreement. The project supports several countries (including Peru, Colombia, the Philippines, Thailand, Indonesia) in developing greenhouse gas mitigation measures in transport. The TRANSfer project is implemented by GIZ and funded by the International Climate Initiative (IKI) of the German Ministry for the Environment, Nature Conservation and Nuclear Safety (BMU) and operates on three levels. Mobilise Prepare Stimulate Facilitating the Preparation of Knowledge products, Training, MobiliseYourCity Mitigation Measures and Dialogue Partnership Standardised support Based on these experiences, TRANSfer The goal of the multi- packages (toolkits) are is sharing and disseminating best stakeholder partnership developed and used for the practises. This is achieved through the MobiliseYourCity, which is preparation of selected development of knowledge products, currently being supported by mitigation measures. As a the organisation of events and trainings, France, Germany and the result, measures can be and the contribution to an increasing European Commission, is that prepared more efficiently, level of ambition. -

Factsheet CENTRALPLAZA NAKHON RATCHASIMA
Factsheet CENTRALPLAZA NAKHON RATCHASIMA – Mahanakorn of Isan CentralPlaza Nakhon Ratchasima, CPN’s 31st shopping centre and the largest mixed-use project in the Northeastern region of Thailand under the concept of “Mahanakorn of Isan”. It includes a shopping center, hotel, convention hall, condominium, outdoor lifestyle market and park, altogether situated on 65 rai of land, with a total investment of 5,160 million baht on the gross area of approximately 114,000 square meters. Its world-class design, conceptualized under the theme “Seasons of Life”, is aimed at unifying diverse cultures and lifestyles through various interactive features that reflect the five seasons to create a “Center of Life”, a space and atmosphere suitable for everybody of all genders and age groups. Grand Opening 3rd November 2017 Location 65-rai plot of land located on Mitrapap Road in Nakhon Ratchasim municipal area, Muang District, Nakhon Ratchasima Province Positioning The largest mixed-use project in the Northeastern region under the concept of “Mahanakorn of ISAN. It includes a shopping center, hotel, convention hall, condominium, outdoor lifestyle market and park. Project Components Shopping Complex: G.F.A. of 114,000 sq.m. / 5 levels (G, 1-4) The lifestyle entertainment shopping complex houses • Central Department Store /1 • Think Space B2S – co-working space equipped with WiFi service, food & beverages by Class Café and B2S store under the concept of “Afterschool Community” • Specialized anchor stores – Tops Super Store, SuperSports, PowerBuy, and OfficeMate • Full-format world-class cinema • DragonWorld, the first in-mall, digitalized and interactive theme park and edutainment center Central Pattana Public Company Limited 1/8 Investor Relations Division / www.cpn.co.th • Over 500 retail shops featuring popular Thai and international brands. -

Final Stop of 2017 WWA Wake Park World Series Bulletin 1: 17Th March 2017 Final Stop of 2017 WWA Wake Park World Series
Final Stop of 2017 WWA Wake Park World Series Bulletin 1: 17th March 2017 Final Stop of 2017 WWA Wake Park World Series #WBWS @TheWWA Final Stop of 2017 WWA WPWS November 25-26, 2017 Final Stop of 2017 WWA Wake Park World Series #WBWS @TheWWA Address: THAI WAKE PARK KORAT, 322 Moo 7, Muang Nakhon Ratchasima, Nakhon Ratchasima, 30000 Thailand. tel: +66 (0) 2904 7722 email: [email protected] facebook: www.facebook.com/thaiwakepark.com The LAST STOP of 2017 Series. The final 2017 champion will be announced and celebrated here in Thailand! Cable Way: - 5 Towers running counter clockwise - Height & Length: 11.5 meters & 680 meters - Built by Rixen - Operating Time: 9:30-18:30 everyday Location: THAI WAKE PARK KORAT, or also known as “TWP Korat”, is located in 80th Birthday Stadium, Nakhon Ratchasima(Korat). It’s just 10 minutes out of Korat City, ideal place to hold the final stop of 2017 Wake Park World Series. Final Stop of 2017 WWA Wake Park World Series #WBWS @TheWWA Park Layout & Features Final Stop of 2017 WWA Wake Park World Series #WBWS @TheWWA Divisions Professional Division Amature Division - Professional Men - Open Men - Professional Features Only - Open Women - Professional Women - Open Wakeskate - Features Only-Women - Open Features Only - Professional Wakeskate Final Stop of 2017 WWA Wake Park World Series #WBWS @TheWWA Description of the Host City Nakhon Ratchasima, otherwise known as Korat, is the largest city in the northeastern province, and the inhabitants of the province are mainly engaged in agricultural activities, growing such diverse crops as rice, sugar cane, sesame, and fruit. -
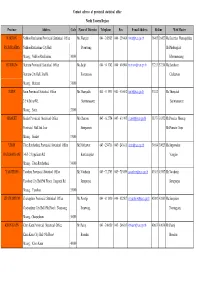
Province Address Code Name of Director Telephone Fax E-Mail
Contact adrress of provincial statistical office North Eastern Region Province Address Code Name of Director Telephone Fax E-mail AddressHotline Web Master NAKHON Nakhon Ratchasima Provincial Statistical Office Ms.Wanpen 044 - 242985 044 - 256406 [email protected] 36465 36427 Ms.Kanittha Wannapakdee RATCHASIMA Nakhon Ratchasima City Hall Poonwong Mr.Phadungkiat Muang , Nakhon Ratchasima 30000 Khmmamuang BURIRUM Burirum Provincial Statistical Office Ms.Saijit 044 - 611742 044 - 614904 [email protected] 37213 37214 Ms.Somboon Burirum City Hall, Jira Rd. Kootaranon Chaleewan Muang , Burirum 31000 SURIN Surin Provincial Statistical Office Ms.Thanyalak 044 - 511931 044 - 516062 [email protected] 37812 Ms.Thanyalak 2/5-6 Sirirat Rd. Surintarasaree Surintarasaree Muang , Surin 32000 SISAKET Sisaket Provincial Statistical Office Mr.Charoon 045 - 612754 045 - 611995 [email protected] 38373 38352 Mr.Preecha Meesup Provincial Hall 2nd floor Siengsanan Mr.Pramote Sopa Muang , Sisaket 33000 UBON Ubon Ratchathani Provincial Statistical Office Mr.Natthawat 045 - 254718 045 - 243811 [email protected] 39014 39023 Ms.Supawadee RATCHATHANI 146/1-2 Uppalisarn Rd. Kanthanaphat Vonglao Muang , Ubon Ratchathani 34000 YASOTHON Yasothon Provincial Statistical Office Mr.Vatcharin 045 - 712703 045 - 713059 [email protected] 43563 43567 Mr.Vatcharin Yasothon City Hall(5th Floor), Jangsanit Rd. Jermprapai Jermprapai Muang , Yasothon 35000 CHAIYAPHUM Chaiyaphum Provincial Statistical Office Ms.Porntip 044 - 811810 044 - 822507 [email protected] 42982 42983 Ms.Sanyakorn -

WHO Thailand Situation Report
Coronavirus disease 2019 (COVID-19) Data as reported by the CCSA mid-day press briefing 27 December 2020 WHO Thailand Situation Report THAILAND SITUATION 6,141 60 1,902 4,161 UPDATE Confirmed Deaths Hospitalized Recovered SPOTLIGHT • On the 27th of December 2020, 121 new cases of laboratory-confirmed COVID-19 were reported by the Ministry of Public Health. The total number of cases reported in Thailand is currently 6,141. • Of these cases, 68 % (4,161) have recovered, 1% (60) have died and 31 % (1,902) are still receiving treatment. No new deaths were reported. • The 121 laboratory-confirmed cases reported today include 8 individuals who entered the country recently and were diagnosed in quarantine facilities. A case is also reported in an individual who entered Thailand recently, but was not in Quarantine. There are 94 new cases classified as ‘domestic transmission’. The remaining 18 cases are in individuals in Samut Sakhon who have been identified through contact tracing and active case finding. • COVID-19 cases linked to the event in Samut Sakhon have now been reported in an additional 38 Provinces. o 18-21 December: Bangkok, Nakhon Pathom, Samut Prakan (3) o 22 December: Chachoengsao, Pathum Thani, Saraburi, Uttradit and Petchaburi (5) o 23 December: Petchabun, Krabi, Kampaeng Phet, Khon Kaen, Ayutthaya, Nakhon Ratchasima, Prachinburi, Phuket, Suphanburi (9) o 24 December: Samut Songkram, Chainat, Pichit, Ang Thong, Nakhon Sawan, Udon Tani, Chaiyaphum, Nakhon Si Thammarat, and Surat Thani (9) o 25 December: Ratchaburi, Chonburi, Loei, Ubon Ratchatani, Songkhla, Nonthaburi (6) o 26 December: Rayong, Trang, Satun, Sukhothai, Nakhon Nayok (5) • In total, 11,620 individuals have been tested through active cases finding / screening in Samut Sakhon, of ths total, 1356 (11.7%) have been confirmed infected with COVID-19. -

Native Burmese Pythons Exhibit Site Fidelity and Preference for Aquatic
www.nature.com/scientificreports OPEN Native Burmese pythons exhibit site fdelity and preference for aquatic habitats in an agricultural mosaic Samantha Nicole Smith1*, Max Dolton Jones1, Benjamin Michael Marshall1, Surachit Waengsothorn2, George A. Gale3 & Colin Thomas Strine1* Animal movement and resource use are tightly linked. Investigating these links to understand how animals use space and select habitats is especially relevant in areas afected by habitat fragmentation and agricultural conversion. We set out to explore the space use and habitat selection of Burmese pythons (Python bivittatus) in a heterogenous, agricultural landscape within the Sakaerat Biosphere Reserve, northeast Thailand. We used VHF telemetry to record the daily locations of seven Burmese pythons and created dynamic Brownian Bridge Movement Models to produce occurrence distributions and model movement extent and temporal patterns. To explore relationships between movement and habitat selection we used integrated step selection functions at both the individual and population level. Burmese pythons had a mean 99% occurrence distribution contour of 98.97 ha (range 9.05– 285.56 ha). Furthermore, our results indicated that Burmese pythons had low mean individual motion variance, indicating infrequent moves and long periods at a single location. In general, Burmese pythons restricted movement and selected aquatic habitats but did not avoid potentially dangerous land use types like human settlements. Although our sample is small, we suggest that Burmese pythons are capitalizing on human disturbed landscapes. Studying and understanding animal movement allows scientists insight into animal behavior1, revealing species’ natural and life histories such as migratory or movement patterns, breeding grounds and seasons, and foraging strategies2–4. -

Measurement of NORM in Building Materials to Assess Radiological
atmosphere Article Measurement of NORM in Building Materials to Assess Radiological Hazards to Human Health and Develop the Standard Guidelines for Residents in Thailand: Case Study in Sand Samples Collected from Seven Northeastern Thailand Provinces Phachirarat Sola 1, Uthaiwan Injarean 1, Roppon Picha 1,*, Chutima Kranrod 2,3 , Chunyapuk Kukusamude 1 and Shinji Tokonami 2,* 1 Thailand Institute of Nuclear Technology (Public Organization), Nakhon Nayok 26120, Thailand; [email protected] (P.S.); [email protected] (U.I.); [email protected] (C.K.) 2 Institute of Radiation Emergency Medicine, Hirosaki University, 66-1 Honcho, Aomori, Hirosaki 036-8564, Japan; [email protected] 3 Natural Radiation Survey and Analysis Research Unit, Department of Nuclear Engineering, Faculty of Engineering, Chulalongkorn University, Bangkok 10330, Thailand * Correspondence: [email protected] (R.P.); [email protected] (S.T.); Tel.: +66-614027945 (R.P.); +172-39-5404 (S.T.) Citation: Sola, P.; Injarean, U.; Picha, R.; Kranrod, C.; Kukusamude, C.; Abstract: A total of 223 sand samples collected from seven provinces in Northeastern Thailand were Tokonami, S. Measurement of NORM analyzed for their gamma radioactivity from naturally occurring radioactive materials (NORMs), in Building Materials to Assess and the data were used to calculate the concentrations of Ra-226, Th-232, and K-40. Radiological Radiological Hazards to Human safety indicators such as the indoor external dose rates (Din), the annual indoor effective dose (Ein), Health and Develop the Standard the activity concentration index (I), the radium equivalent activity (Raeq), the external hazard index Guidelines for Residents in Thailand: Case Study in Sand Samples (Hex), the internal haphazard index (Hin), and the excess lifetime cancer risk (ELCR) were calculated. -

Comprehensive Planning of Eurasian Transport Corridors
Thailand Country Presentation Workshop on Strengthening Transport Connectivity among CLMV-T 9-10 October 2018, Yangon, Myanmar Outline • Greater Mekong Sub region Economic Corridor & Other Economic Corridor • National Strategies for Transport Development & R3B R3A Transport’s Infrastructure Development Plans • Current status of Land Transportation between R R Thailand & Neighbor Countries 9 2 R 1 2 Greater Mekong Sub region Economic Corridor & Other Economic Corridor 3 GMS Economic Corridors GMS Route in Thailand Southern Economic Corridor (SEC) R1 Central Subcorridor Bangkok- Aranyaprathet - Phnom Penh-Ho Chi Minh City-Vung Tau 81 km. R10 Southern Coastal Subcorridor Bangkok-Trat-Koh Kong-Kampot-Ha Tien-Ca Mau City-Nam Can R3B R3A East-West Economic Corridor (EWEC) 1,450 km R2 (R9) : Mawlamyine-Myawaddy - Mae Sot- Phitsanulok-Khon Kaen-Kalasin-Mukdahan - R9 R2 Savannakhet-Dansavanh-Lao Bao-Hue-Dong Ha-Da Nang North-South Economic Corridor (NSEC) R3 R1 R3A: 4th Thailand - Laos friendship bridge Chiang Khong – Huai Xai – Louangnamtha – Mo Han – Boten –Jing Hong – Yuxi - Kunming (1,140 km.) R3B: Chiang Rai (Mae Sai check point) -Ta Chi Leick - Chiang Tung –Jing Hong-Kunming (1,040 km.) 5 New Configuration of EWEC, NSEC, SEC Changes in the Configuration of Economic Corridors The following changes in the configuration of the GMS economic corridors are recommended based on the foregoing discussion on the realignment and/or extension of the economic corridors: (i) Include an extension at the western end of EWEC to Yangon–Thilawa using the Myawaddy–Kawkareik–Eindu–Hpa-An– Thaton–Kyaikto–Payagi– Bago–Yangon–Thilawa route, with a possible extension to Pathein. -

Bangkok-Chiang Mai HSR Project (672 Km)
4-year Performance The Ministry of Transport (MOT) under my leadership has been striving to enhance the quality of life through improved transportation systems. The MOT is developing transport networks across the country to provide multimodal interconnection for safer and more convenient travel and boosting economic activities. In this pursuit, the MOT proposed the eight-year These infrastructure schemes aim to facilitate rapid Thailand’s Transport Infrastructure Development Strategy and convenient mobility, improve living conditions and boost (2015-2022) to define the framework for development of Thailand’s competitiveness. The projects will help to unlock transport networks in five aspects, namely intercity railway national economic potential and forge better connectivity in networks, public transit systems for addressing traffic the region. I have emphasized that all responsible agencies issues, highway networks for providing links between major must operate with great efficiency and transparency and that production bases and with neighboring countries, water the fiscal budget should be allocated fairly and regularly as transport systems, and aviation enhancement. planned. General Prayut Chan-o-cha Prime Minister 2 -year Performance of Ministry of Transport 4For Happiness of Thai People In line with the Prime Minister’s policies, the Ministry of Transport (MOT) has been implementing infrastructure development to make Thailand a leading member of the Association of Southeast Asian Nations (ASEAN). This has included the development of land, rail, water and aviation systems at domestic and cross-border levels to facilitate safe, convenient and inclusive transport and logistical measures generally. This will help to enhance incomes, contentment and quality of life for the Thai people as well as empower national economic competitiveness and upgrade Thailand into a regional transport hub.