Plotting the Graph of a Function
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Plotting, Derivatives, and Integrals for Teaching Calculus in R
Plotting, Derivatives, and Integrals for Teaching Calculus in R Daniel Kaplan, Cecylia Bocovich, & Randall Pruim July 3, 2012 The mosaic package provides a command notation in R designed to make it easier to teach and to learn introductory calculus, statistics, and modeling. The principle behind mosaic is that a notation can more effectively support learning when it draws clear connections between related concepts, when it is concise and consistent, and when it suppresses extraneous form. At the same time, the notation needs to mesh clearly with R, facilitating students' moving on from the basics to more advanced or individualized work with R. This document describes the calculus-related features of mosaic. As they have developed histori- cally, and for the main as they are taught today, calculus instruction has little or nothing to do with statistics. Calculus software is generally associated with computer algebra systems (CAS) such as Mathematica, which provide the ability to carry out the operations of differentiation, integration, and solving algebraic expressions. The mosaic package provides functions implementing he core operations of calculus | differen- tiation and integration | as well plotting, modeling, fitting, interpolating, smoothing, solving, etc. The notation is designed to emphasize the roles of different kinds of mathematical objects | vari- ables, functions, parameters, data | without unnecessarily turning one into another. For example, the derivative of a function in mosaic, as in mathematics, is itself a function. The result of fitting a functional form to data is similarly a function, not a set of numbers. Traditionally, the calculus curriculum has emphasized symbolic algorithms and rules (such as xn ! nxn−1 and sin(x) ! cos(x)). -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -
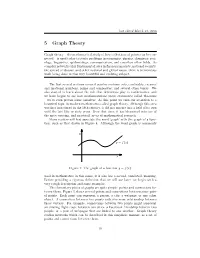
5 Graph Theory
last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples. -

Lecture 11: Graphs of Functions Definition If F Is a Function With
Lecture 11: Graphs of Functions Definition If f is a function with domain A, then the graph of f is the set of all ordered pairs f(x; f(x))jx 2 Ag; that is, the graph of f is the set of all points (x; y) such that y = f(x). This is the same as the graph of the equation y = f(x), discussed in the lecture on Cartesian co-ordinates. The graph of a function allows us to translate between algebra and pictures or geometry. A function of the form f(x) = mx+b is called a linear function because the graph of the corresponding equation y = mx + b is a line. A function of the form f(x) = c where c is a real number (a constant) is called a constant function since its value does not vary as x varies. Example Draw the graphs of the functions: f(x) = 2; g(x) = 2x + 1: Graphing functions As you progress through calculus, your ability to picture the graph of a function will increase using sophisticated tools such as limits and derivatives. The most basic method of getting a picture of the graph of a function is to use the join-the-dots method. Basically, you pick a few values of x and calculate the corresponding values of y or f(x), plot the resulting points f(x; f(x)g and join the dots. Example Fill in the tables shown below for the functions p f(x) = x2; g(x) = x3; h(x) = x and plot the corresponding points on the Cartesian plane. -
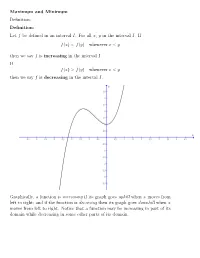
Maximum and Minimum Definition
Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing. -

Chapter 3. Linearization and Gradient Equation Fx(X, Y) = Fxx(X, Y)
Oliver Knill, Harvard Summer School, 2010 An equation for an unknown function f(x, y) which involves partial derivatives with respect to at least two variables is called a partial differential equation. If only the derivative with respect to one variable appears, it is called an ordinary differential equation. Examples of partial differential equations are the wave equation fxx(x, y) = fyy(x, y) and the heat Chapter 3. Linearization and Gradient equation fx(x, y) = fxx(x, y). An other example is the Laplace equation fxx + fyy = 0 or the advection equation ft = fx. Paul Dirac once said: ”A great deal of my work is just playing with equations and see- Section 3.1: Partial derivatives and partial differential equations ing what they give. I don’t suppose that applies so much to other physicists; I think it’s a peculiarity of myself that I like to play about with equations, just looking for beautiful ∂ mathematical relations If f(x, y) is a function of two variables, then ∂x f(x, y) is defined as the derivative of the function which maybe don’t have any physical meaning at all. Sometimes g(x) = f(x, y), where y is considered a constant. It is called partial derivative of f with they do.” Dirac discovered a PDE describing the electron which is consistent both with quan- respect to x. The partial derivative with respect to y is defined similarly. tum theory and special relativity. This won him the Nobel Prize in 1933. Dirac’s equation could have two solutions, one for an electron with positive energy, and one for an electron with ∂ antiparticle One also uses the short hand notation fx(x, y)= ∂x f(x, y). -

2.8 the Derivative As a Function
2 Derivatives Copyright © Cengage Learning. All rights reserved. 2.8 The Derivative as a Function Copyright © Cengage Learning. All rights reserved. The Derivative as a Function We have considered the derivative of a function f at a fixed number a: Here we change our point of view and let the number a vary. If we replace a in Equation 1 by a variable x, we obtain 3 The Derivative as a Function Given any number x for which this limit exists, we assign to x the number f′(x). So we can regard f′ as a new function, called the derivative of f and defined by Equation 2. We know that the value of f′ at x, f′(x), can be interpreted geometrically as the slope of the tangent line to the graph of f at the point (x, f(x)). The function f′ is called the derivative of f because it has been “derived” from f by the limiting operation in Equation 2. The domain of f′ is the set {x | f′(x) exists} and may be smaller than the domain of f. 4 Example 1 – Derivative of a Function given by a Graph The graph of a function f is given in Figure 1. Use it to sketch the graph of the derivative f′. Figure 1 5 Example 1 – Solution We can estimate the value of the derivative at any value of x by drawing the tangent at the point (x, f(x)) and estimating its slope. For instance, for x = 5 we draw the tangent at P in Figure 2(a) and estimate its slope to be about , so f′(5) ≈ 1.5. -

Laplace Transforms SCHOOL of ENGINEERING & BUILT
SCHOOL OF ENGINEERING & BUILT ENVIRONMENT Mathematics Laplace Transforms 1. Introduction ……………………………………. 1 2. Definition ………………………………………. 2 3. Properties of the Laplace Transform …………… 4 4. Inverse Laplace Transforms …………………… 6 5. Using Laplace Transforms to Solve ODEs ……. 9 6. The Step Function ……………………………... 11 7. The Dirac Delta Function ……………………… 20 8. Convolution ……………………………………. 25 9. A Note on Control Theory …………………….. 26 Tutorial Exercises ……………………………… 27 Answers to Tutorial Exercises …………………. 33 1 Laplace Transforms 1) Introduction The idea of transforming a “difficult” problem into an “easier” problem is one that is used widely in mathematics. Diagrammatically we have Problem Transform Transformed Problem Difficult Solve Solution Transformed Inverse Solution Transform There are many types of transforms available to mathematicians, engineers and scientists. We are going to examine one such transformation, the Laplace transform, which can be used to solve certain types of differential equations and also has applications in control theory. 2) Definition The Laplace transform operates on functions of t . Given a function f (t ) we define its Laplace transform as ∞ L[ f (t ) ] = f (t ) e − s t dt 0 where s is termed the Laplace variable. We sometimes denote the Laplace transform by F ( s ) or f . We start off with a function of t and end up with a function of s ; s is, in fact, a complex variable, but this need not concern us too much. Because the function of t is often some form of time signal, we often talk about moving from the time domain to the Laplace domain when we perform a Laplace transformation. Note: Laplace transforms are only concerned with functions where t ≥ 0. -

3.2 the Graph of a Function
✎ ✍3.2 ✌ The graph of a function Introduction A very useful pictorial representation of a function is the graph. On this leaflet we remind you of important conventions when graph plotting. 1. The graph of a function Consider the function f(x)=5x +4. We can choose several values for the input and calculate the corresponding outputs. We have done this for integer values of x between −3 and 3 and the results are shown in the table. x −3 −2 −10123 f(x) −11 −6 −1491419 To plot the graph we first draw a pair of axes - a vertical axis and a horizontal axis. These are drawn at right-angles to each other and intersect at the origin O as shown below. y = f(x) y =5x +4 vertical axis 15 10 The point with coordinates (2, 14) 5 -3 -2 -1 O 123x -5 horizontal axis -10 Each pair of input and output values can be represented on a graph by a single point. The input values are measured along the horizontal axis and the output values along the vertical axis. A uniform scale is drawn on each axis sufficient to accommodate all the required points. The points plotted in this way are then joined together, in this case by a straight line. This is the graph of the function. Each point on the graph can be represented by a pair of coordinates in the form (x, f(x)). Each axis should be labelled to show its variable. 2. Dependent and independent variables The horizontal axis is often called the x axis. -

The Laplace Transform (Intro)
24 The Laplace Transform (Intro) The Laplace transform is a mathematical tool based on integration that has a number of appli- cations. It particular, it can simplify the solving of many differential equations. We will find it particularly useful when dealing with nonhomogeneous equations in which the forcing func- tions are not continuous. This makes it a valuable tool for engineers and scientists dealing with “real-world” applications. By the way, the Laplace transform is just one of many “integral transforms” in general use. Conceptually and computationally, it is probably the simplest. If you understand the Laplace transform, then you will find it much easier to pick up the other transforms as needed. 24.1 Basic Definition and Examples Definition, Notation and Other Basics Let f be a ‘suitable’ function (more on that later). The Laplace transform of f , denoted by either F or L[ f ] , is the function given by ∞ st F(s) L[ f ] f (t)e− dt . (24.1) = |s = Z0 !◮Example 24.1: For our first example, let us use 1 if t 2 f (t) ≤ . = ( 0 if 2 < t This is the relatively simple discontinuous function graphed in figure 24.1a. To compute the Laplace transform of this function, we need to break the integral into two parts: ∞ st F(s) L[ f ] f (t)e− dt = |s = Z0 2 st ∞ st f (t) e− dt f (t) e− dt = 0 + 2 Z 1 Z 0 2 2 |{zst} ∞ |{z} st e− dt 0 dt e− dt . = + = Z0 Z2 Z0 471 472 The Laplace Transform 2 1 1 0 1 2 T 2 S (a) (b) Figure 24.1: The graph of (a) the discontinuous function f (t) from example 24.1 and (b) its Laplace transform F(s) . -

Integration Not for Sale
Not for Sale 5 Integration Chapter Preview We are now at a critical point in the calculus story. Many would 5.1 Approximating Areas argue that this chapter is the cornerstone of calculus because it explains the relationship under Curves between the two processes of calculus: differentiation and integration. We begin by ex- 5.2 Definite Integrals plaining why finding the area of regions bounded by the graphs of functions is such an important problem in calculus. Then you will see how antiderivatives lead to definite in- 5.3 Fundamental Theorem tegrals, which are used to solve the area problem. But there is more to the story. You will of Calculus also see the remarkable connection between derivatives and integrals, which is expressed 5.4 Working with Integrals in the Fundamental Theorem of Calculus. In this chapter, we develop key properties of 5.5 Substitution Rule definite integrals, investigate a few of their many applications, and present the first of sev- eral powerful techniques for evaluating definite integrals. 5.1 Approximating Areas under Curves The derivative of a function is associated with rates of change and slopes of tangent lines. We also know that antiderivatives (or indefinite integrals) reverse the derivative operation. Figure 5.1 summarizes our current understanding and raises the question: What is the geo- metric meaning of the integral? The following example reveals a clue. f(x) f Ј(x) ͵ f (x)dx Slopes of ??? tangent lines Figure 5.1 Area under a Velocity Curve Consider an object moving along a line with a known position function. -

Infinitesimal Methods in Mathematical Economics
Infinitesimal Methods in Mathematical Economics Robert M. Anderson1 Department of Economics and Department of Mathematics University of California at Berkeley Berkeley, CA 94720, U.S.A. and Department of Economics Johns Hopkins University Baltimore, MD 21218, U.S.A. January 20, 2008 1The author is grateful to Marc Bettz¨uge, Don Brown, Hung- Wen Chang, G´erard Debreu, Eddie Dekel-Tabak, Greg Engl, Dmitri Ivanov, Jerry Keisler, Peter Loeb, Paul MacMillan, Mike Magill, Andreu Mas-Colell, Max Stinchcombe, Cathy Wein- berger and Bill Zame for their helpful comments. Financial sup- port from Deutsche Forschungsgemeinschaft, Gottfried-Wilhelm- Leibniz-F¨orderpreis is gratefully acknowledged. Contents 0Preface v 1 Nonstandard Analysis Lite 1 1.1 When is Nonstandard Analysis Useful? . 1 1.1.1 Large Economies . 2 1.1.2 Continuum of Random Variables . 4 1.1.3 Searching For Elementary Proofs . 4 1.2IdealElements................. 5 1.3Ultraproducts.................. 6 1.4InternalandExternalSets........... 9 1.5NotationalConventions............. 11 1.6StandardModels................ 12 1.7 Superstructure Embeddings . 14 1.8AFormalLanguage............... 16 1.9TransferPrinciple................ 16 1.10Saturation.................... 18 1.11InternalDefinitionPrinciple.......... 19 1.12 Nonstandard Extensions, or Enough Already with the Ultraproducts . 20 1.13HyperfiniteSets................. 21 1.14 Nonstandard Theorems Have Standard Proofs 22 2 Nonstandard Analysis Regular 23 2.1 Warning: Do Not Read this Chapter . 23 i ii CONTENTS 2.2AFormalLanguage............... 23 2.3 Extensions of L ................. 25 2.4 Assigning Truth Value to Formulas . 28 2.5 Interpreting Formulas in Superstructure Em- beddings..................... 32 2.6TransferPrinciple................ 33 2.7InternalDefinitionPrinciple.......... 34 2.8NonstandardExtensions............ 35 2.9TheExternalLanguage............. 36 2.10TheConservationPrinciple.......... 37 3RealAnalysis 39 3.1Monads..................... 39 3.2OpenandClosedSets............. 44 3.3Compactness.................