DOCSLIB.ORG

Stat 520 Forecasting and Time Series

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Stat 520 Forecasting and Time Series STAT 520 FORECASTING AND TIME SERIES Fall, 2013 Lecture Notes Joshua M. Tebbs Department of Statistics University of South Carolina TABLE OF CONTENTS STAT 520, J. TEBBS Contents 1 Introduction and Examples 1 2 Fundamental Concepts 20 2.1 Summary of important distribution theory . 20 2.1.1 Univariate random variables . 20 2.1.2 Bivariate random vectors . 22 2.1.3 Multivariate extensions and linear combinations . 26 2.1.4 Miscellaneous . 27 2.2 Time series and stochastic processes . 28 2.3 Means, variances, and covariances . 29 2.4 Some (named) stochastic processes . 29 2.5 Stationarity . 38 3 Modeling Deterministic Trends 44 3.1 Introduction . 44 3.2 Estimation of a constant mean . 46 3.3 Regression methods . 51 3.3.1 Straight line regression . 51 3.3.2 Polynomial regression . 57 3.3.3 Seasonal means model . 61 3.3.4 Cosine trend model . 64 3.4 Interpreting regression output . 68 3.5 Residual analysis (model diagnostics) . 70 3.5.1 Assessing normality . 71 3.5.2 Assessing independence . 73 3.5.3 Sample autocorrelation function . 76 i TABLE OF CONTENTS STAT 520, J. TEBBS 4 Models for Stationary Time Series 80 4.1 Introduction . 80 4.2 Moving average processes . 81 4.2.1 MA(1) process . 81 4.2.2 MA(2) process . 85 4.2.3 MA(q) process . 87 4.3 Autoregressive processes . 88 4.3.1 AR(1) process . 89 4.3.2 AR(2) process . 94 4.3.3 AR(p) process . 103 4.4 Invertibility . 105 4.5 Autoregressive moving average (ARMA) processes . 107 5 Models for Nonstationary Time Series 113 5.1 Introduction . 113 5.2 Autoregressive integrated moving average (ARIMA) models . 118 5.2.1 IMA(1,1) process . 122 5.2.2 IMA(2,2) process . 123 5.2.3 ARI(1,1) process . 125 5.2.4 ARIMA(1,1,1) process . 125 5.3 Constant terms in ARIMA models . 127 5.4 Transformations . 129 6 Model Specification 136 6.1 Introduction . 136 6.2 The sample autocorrelation function . 136 6.3 The partial autocorrelation function . 143 6.4 The extended autocorrelation function . 155 ii TABLE OF CONTENTS STAT 520, J. TEBBS 6.5 Nonstationarity . 163 6.6 Other model selection methods . 170 6.7 Summary . 173 7 Estimation 175 7.1 Introduction . 175 7.2 Method of moments . 176 7.2.1 Autoregressive models . 176 7.2.2 Moving average models . 178 7.2.3 Mixed ARMA models . 179 7.2.4 White noise variance . 179 7.2.5 Examples . 180 7.3 Least squares estimation . 185 7.3.1 Autoregressive models . 185 7.3.2 Moving average models . 187 7.3.3 Mixed ARMA models . 188 7.3.4 White noise variance . 189 7.3.5 Examples . 189 7.4 Maximum likelihood estimation . 197 7.4.1 Large-sample properties of MLEs . 200 7.4.2 Examples . 202 8 Model Diagnostics 208 8.1 Introduction . 208 8.2 Residual analysis . 209 8.2.1 Normality and independence . 211 8.2.2 Residual ACF . 215 8.3 Overfitting . 228 iii TABLE OF CONTENTS STAT 520, J. TEBBS 9 Forecasting 231 9.1 Introduction . 231 9.2 Deterministic trend models . 233 9.3 ARIMA models . 237 9.3.1 AR(1) . 238 9.3.2 MA(1) . 244 9.3.3 ARMA(p; q).............................. 248 9.3.4 Nonstationary models . 253 9.4 Prediction intervals . 258 9.4.1 Deterministic trend models . 259 9.4.2 ARIMA models . 261 9.5 Forecasting transformed series . 263 9.5.1 Differencing . 263 9.5.2 Log-transformed series . 265 10 Seasonal ARIMA Models 267 10.1 Introduction . 267 10.2 Purely seasonal (stationary) ARMA models . 269 10.2.1 MA(Q)s ................................ 269 10.2.2 AR(P )s ................................ 274 10.2.3 ARMA(P; Q)s ............................. 278 10.3 Multiplicative seasonal (stationary) ARMA models . 280 10.4 Nonstationary seasonal ARIMA (SARIMA) models . 290 10.5 Additional topics . 306 iv CHAPTER 1 STAT 520, J. TEBBS 1 Introduction and Examples Complementary reading: Chapter 1 (CC). TERMINOLOGY :A time series is a sequence of ordered data. The \ordering" refers generally to time, but other orderings could be envisioned (e.g., over space, etc.). In this class, we will be concerned exclusively with time series that are • measured on a single continuous random variable Y • equally spaced in discrete time; that is, we will have a single realization of Y at each second, hour, day, month, year, etc. UBIQUITY : Time series data arise in a variety of fields. Here are just a few examples. • In business, we observe daily stock prices, weekly interest rates, quarterly sales, monthly supply figures, annual earnings, etc. • In agriculture, we observe annual yields (e.g., crop production), daily crop prices, annual herd sizes, etc. • In engineering, we observe electric signals, voltage measurements, etc. • In natural sciences, we observe chemical yields, turbulence in ocean waves, earth tectonic plate positions, etc. • In medicine, we observe EKG measurements on patients, drug concentrations, blood pressure readings, etc. • In epidemiology, we observe the number of flu cases per day, the number of health-care clinic visits per week, annual tuberculosis counts, etc. • In meteorology, we observe daily high temperatures, annual rainfall, hourly wind speeds, earthquake frequency, etc. • In social sciences, we observe annual birth and death rates, accident frequencies, crime rates, school enrollments, etc. PAGE 1 CHAPTER 1 STAT 520, J. TEBBS Global temperature deviations Global temperature −0.4 −0.2 0.0 0.2 0.4 1860 1880 1900 1920 1940 1960 1980 2000 Year Figure 1.1: Global temperature data. The data are a combination of land-air average temperature anomalies, measured in degrees Centigrade. Example 1.1. Global temperature data. \Global warming" refers to an increase in the average temperature of the Earth's near-surface air and oceans since the mid-20th century and its projected continuation. The data in Figure 1.1 are annual temperature deviations (1856-1997) in deg C, measured from a baseline average. • Data file: globaltemps • There are n = 142 observations. • Measurements are taken each year. • What are the noticeable patterns? • Predictions? (Are we doomed?) PAGE 2 CHAPTER 1 STAT 520, J. TEBBS Amount of milk produced 1300 1400 1500 1600 1700 1994 1996 1998 2000 2002 2004 2006 Year Figure 1.2: United States milk production data. Monthly production figures, measured in millions of pounds, from January, 1994 to December, 2005. Example 1.2. Milk production data. Commercial dairy farming produces the vast majority of milk in the United States. The data in Figure 1.2 are the monthly U.S. milk production (in millions of pounds) from January, 1994 to December, 2005. • Data file: milk (TSA) • There are n = 144 observations. • Measurements are taken each month. • What are the noticeable patterns? • Predictions? PAGE 3 CHAPTER 1 STAT 520, J. TEBBS CREF stock values 170 180 190 200 210 220 0 100 200 300 400 500 Time Figure 1.3: CREF stock data. Daily values of one unit of CREF stock values: August 26, 2004 to August 15, 2006. Example 1.3. CREF stock data. TIAA-CREF is the leading provider of retirement accounts and products to employees in academic, research, medical, and cultural in- stitutions. The data in Figure 1.3 are daily values of one unit of the CREF (College Retirement Equity Fund) stock fund from 8/26/04 to 8/15/06. • Data file: CREF (TSA) • There are n = 501 observations. • Measurements are taken each trading day. • What are the noticeable patterns? • Predictions? (My retirement depends on these!) PAGE 4 CHAPTER 1 STAT 520, J. TEBBS Number of homeruns 50 100 150 200 1920 1940 1960 1980 2000 Year Figure 1.4: Homerun data. Number of homeruns hit by the Boston Red Sox each year during 1909-2010. Example 1.4. Homerun data. The Boston Red Sox are a professional baseball team based in Boston, Massachusetts, and a member of the Major League Baseball's American League Eastern Division. The data in Figure 1.4 are the number of homeruns hit by the team each year from 1909 to 2010. Source: Ted Hornback (Spring, 2010). • Data file: homeruns • There are n = 102 observations. • Measurements are taken each year. • What are the noticeable patterns? • Predictions? PAGE 5 CHAPTER 1 STAT 520, J. TEBBS Number of earthquakes (7.0 or greater) 5 10 15 20 25 30 35 40 1900 1920 1940 1960 1980 2000 Year Figure 1.5: Earthquake data. Number of \large" earthquakes per year from 1900-1998. Example 1.5. Earthquake data. An earthquake occurs when there is a sudden release of energy in the Earth's crust. Earthquakes are caused mostly by rupture of geological faults, but also by other events such as volcanic activity, landslides, mine blasts, and nuclear tests. The data in Figure 1.5 are the number of global earthquakes annually (with intensities of 7.0 or greater) during 1900-1998. Source: Craig Whitlow (Spring, 2010). • Data file: earthquake • There are n = 99 observations. • Measurements are taken each year. • What are the noticeable patterns? • Predictions? PAGE 6 CHAPTER 1 STAT 520, J. TEBBS USC Columbia fall enrollment USC Columbia fall 5000 10000 15000 20000 25000 1960 1970 1980 1990 2000 2010 Year Figure 1.6: University of South Carolina fall enrollment data. Number of students reg- istered for classes.
Load more

Recommended publications
  • Chapter 2 Time Series and Forecasting
    Chapter 2 Time series and Forecasting 2.1 Introduction Data are frequently recorded at regular time intervals, for instance, daily stock market indices, the monthly rate of inflation or annual profit figures. In this Chapter we think about how to display and model such data. We will consider how to detect trends and seasonal effects and then use these to make forecasts. As well as review the methods covered in MAS1403, we will also consider a class of time series models known as autore- gressive moving average models. Why is this topic useful? Well, making forecasts allows organisations to make better decisions and to plan more efficiently. For instance, reliable forecasts enable a retail outlet to anticipate demand, hospitals to plan staffing levels and manufacturers to keep appropriate levels of inventory. 2.2 Displaying and describing time series A time series is a collection of observations made sequentially in time. When observations are made continuously, the time series is said to be continuous; when observations are taken only at specific time points, the time series is said to be discrete. In this course we consider only discrete time series, where the observations are taken at equal intervals. The first step in the analysis of time series is usually to plot the data against time, in a time series plot. Suppose we have the following four–monthly sales figures for Turner’s Hangover Cure as described in Practical 2 (in thousands of pounds): Jan–Apr May–Aug Sep–Dec 2006 8 10 13 2007 10 11 14 2008 10 11 15 2009 11 13 16 We could enter these data into a single column (say column C1) in Minitab, and then click on Graph–Time Series Plot–Simple–OK; entering C1 in Series and then clicking OK gives the graph shown in figure 2.1.
    [Show full text]
  • Demand Forecasting
    BIZ2121 Production & Operations Management Demand Forecasting Sung Joo Bae, Associate Professor Yonsei University School of Business Unilever Customer Demand Planning (CDP) System Statistical information: shipment history, current order information Demand-planning system with promotional demand increase, and other detailed information (external market research, internal sales projection) Forecast information is relayed to different distribution channel and other units Connecting to POS (point-of-sales) data and comparing it to forecast data is a very valuable ways to update the system Results: reduced inventory, better customer service Forecasting Forecasts are critical inputs to business plans, annual plans, and budgets Finance, human resources, marketing, operations, and supply chain managers need forecasts to plan: ◦ output levels ◦ purchases of services and materials ◦ workforce and output schedules ◦ inventories ◦ long-term capacities Forecasting Forecasts are made on many different variables ◦ Uncertain variables: competitor strategies, regulatory changes, technological changes, processing times, supplier lead times, quality losses ◦ Different methods are used Judgment, opinions of knowledgeable people, average of experience, regression, and time-series techniques ◦ No forecast is perfect Constant updating of plans is important Forecasts are important to managing both processes and supply chains ◦ Demand forecast information can be used for coordinating the supply chain inputs, and design of the internal processes (especially
    [Show full text]
  • Generalized Linear Models and Generalized Additive Models
    00:34 Friday 27th February, 2015 Copyright ©Cosma Rohilla Shalizi; do not distribute without permission updates at http://www.stat.cmu.edu/~cshalizi/ADAfaEPoV/ Chapter 13 Generalized Linear Models and Generalized Additive Models [[TODO: Merge GLM/GAM and Logistic Regression chap- 13.1 Generalized Linear Models and Iterative Least Squares ters]] [[ATTN: Keep as separate Logistic regression is a particular instance of a broader kind of model, called a gener- chapter, or merge with logis- alized linear model (GLM). You are familiar, of course, from your regression class tic?]] with the idea of transforming the response variable, what we’ve been calling Y , and then predicting the transformed variable from X . This was not what we did in logis- tic regression. Rather, we transformed the conditional expected value, and made that a linear function of X . This seems odd, because it is odd, but it turns out to be useful. Let’s be specific. Our usual focus in regression modeling has been the condi- tional expectation function, r (x)=E[Y X = x]. In plain linear regression, we try | to approximate r (x) by β0 + x β. In logistic regression, r (x)=E[Y X = x] = · | Pr(Y = 1 X = x), and it is a transformation of r (x) which is linear. The usual nota- tion says | ⌘(x)=β0 + x β (13.1) · r (x) ⌘(x)=log (13.2) 1 r (x) − = g(r (x)) (13.3) defining the logistic link function by g(m)=log m/(1 m). The function ⌘(x) is called the linear predictor. − Now, the first impulse for estimating this model would be to apply the transfor- mation g to the response.
    [Show full text]
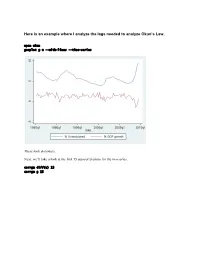
  • Here Is an Example Where I Analyze the Lags Needed to Analyze Okun's
    Here is an example where I analyze the lags needed to analyze Okun’s Law. open okun gnuplot g u --with-lines --time-series These look stationary. Next, we’ll take a look at the first 15 autocorrelations for the two series. corrgm diff(u) 15 corrgm g 15 These are autocorrelated and so are these. I would expect that a simple regression will not be sufficient to model this relationship. Let’s try anyway. Run a simple regression and look at the residuals ols diff(u) const g series ehat=$uhat gnuplot ehat --with-lines --time-series These look positively autocorrelated to me. Notice how the residuals fall below zero for a while, then rise above for a while, and repeat this pattern. Take a look at the correlogram. The first autocorrelation is significant. More lags of D.u or g will probably fix this. LM test of residuals smpl 1985.2 2009.3 ols diff(u) const g modeltab add modtest 1 --autocorr --quiet modtest 2 --autocorr --quiet modtest 3 --autocorr --quiet modtest 4 --autocorr --quiet Breusch-Godfrey test for first-order autocorrelation Alternative statistic: TR^2 = 6.576105, with p-value = P(Chi-square(1) > 6.5761) = 0.0103 Breusch-Godfrey test for autocorrelation up to order 2 Alternative statistic: TR^2 = 7.922218, with p-value = P(Chi-square(2) > 7.92222) = 0.019 Breusch-Godfrey test for autocorrelation up to order 3 Alternative statistic: TR^2 = 11.200978, with p-value = P(Chi-square(3) > 11.201) = 0.0107 Breusch-Godfrey test for autocorrelation up to order 4 Alternative statistic: TR^2 = 11.220956, with p-value = P(Chi-square(4) > 11.221) = 0.0242 Yep, that’s not too good.
    [Show full text]
  • Moving Average Filters
    CHAPTER 15 Moving Average Filters The moving average is the most common filter in DSP, mainly because it is the easiest digital filter to understand and use. In spite of its simplicity, the moving average filter is optimal for a common task: reducing random noise while retaining a sharp step response. This makes it the premier filter for time domain encoded signals. However, the moving average is the worst filter for frequency domain encoded signals, with little ability to separate one band of frequencies from another. Relatives of the moving average filter include the Gaussian, Blackman, and multiple- pass moving average. These have slightly better performance in the frequency domain, at the expense of increased computation time. Implementation by Convolution As the name implies, the moving average filter operates by averaging a number of points from the input signal to produce each point in the output signal. In equation form, this is written: EQUATION 15-1 Equation of the moving average filter. In M &1 this equation, x[ ] is the input signal, y[ ] is ' 1 % y[i] j x [i j ] the output signal, and M is the number of M j'0 points used in the moving average. This equation only uses points on one side of the output sample being calculated. Where x[ ] is the input signal, y[ ] is the output signal, and M is the number of points in the average. For example, in a 5 point moving average filter, point 80 in the output signal is given by: x [80] % x [81] % x [82] % x [83] % x [84] y [80] ' 5 277 278 The Scientist and Engineer's Guide to Digital Signal Processing As an alternative, the group of points from the input signal can be chosen symmetrically around the output point: x[78] % x[79] % x[80] % x[81] % x[82] y[80] ' 5 This corresponds to changing the summation in Eq.
    [Show full text]
  • Stochastic Process - Introduction
    Stochastic Process - Introduction • Stochastic processes are processes that proceed randomly in time. • Rather than consider fixed random variables X, Y, etc. or even sequences of i.i.d random variables, we consider sequences X0, X1, X2, …. Where Xt represent some random quantity at time t. • In general, the value Xt might depend on the quantity Xt-1 at time t-1, or even the value Xs for other times s < t. • Example: simple random walk . week 2 1 Stochastic Process - Definition • A stochastic process is a family of time indexed random variables Xt where t belongs to an index set. Formal notation, { t : ∈ ItX } where I is an index set that is a subset of R. • Examples of index sets: 1) I = (-∞, ∞) or I = [0, ∞]. In this case Xt is a continuous time stochastic process. 2) I = {0, ±1, ±2, ….} or I = {0, 1, 2, …}. In this case Xt is a discrete time stochastic process. • We use uppercase letter {Xt } to describe the process. A time series, {xt } is a realization or sample function from a certain process. • We use information from a time series to estimate parameters and properties of process {Xt }. week 2 2 Probability Distribution of a Process • For any stochastic process with index set I, its probability distribution function is uniquely determined by its finite dimensional distributions. •The k dimensional distribution function of a process is defined by FXX x,..., ( 1 x,..., k ) = P( Xt ≤ 1 ,..., xt≤ X k) x t1 tk 1 k for anyt 1 ,..., t k ∈ I and any real numbers x1, …, xk .
    [Show full text]
  • Parameters Estimation for Asymmetric Bifurcating Autoregressive Processes with Missing Data
    Electronic Journal of Statistics ISSN: 1935-7524 Parameters estimation for asymmetric bifurcating autoregressive processes with missing data Benoîte de Saporta Université de Bordeaux, GREThA CNRS UMR 5113, IMB CNRS UMR 5251 and INRIA Bordeaux Sud Ouest team CQFD, France e-mail: [email protected] and Anne Gégout-Petit Université de Bordeaux, IMB, CNRS UMR 525 and INRIA Bordeaux Sud Ouest team CQFD, France e-mail: [email protected] and Laurence Marsalle Université de Lille 1, Laboratoire Paul Painlevé, CNRS UMR 8524, France e-mail: [email protected] Abstract: We estimate the unknown parameters of an asymmetric bi- furcating autoregressive process (BAR) when some of the data are missing. In this aim, we model the observed data by a two-type Galton-Watson pro- cess consistent with the binary Bee structure of the data. Under indepen- dence between the process leading to the missing data and the BAR process and suitable assumptions on the driven noise, we establish the strong con- sistency of our estimators on the set of non-extinction of the Galton-Watson process, via a martingale approach. We also prove a quadratic strong law and the asymptotic normality. AMS 2000 subject classifications: Primary 62F12, 62M09; secondary 60J80, 92D25, 60G42. Keywords and phrases: least squares estimation, bifurcating autoregres- sive process, missing data, Galton-Watson process, joint model, martin- gales, limit theorems. arXiv:1012.2012v3 [math.PR] 27 Sep 2011 1. Introduction Bifurcating autoregressive processes (BAR) generalize autoregressive (AR) pro- cesses, when the data have a binary tree structure. Typically, they are involved in modeling cell lineage data, since each cell in one generation gives birth to two offspring in the next one.
    [Show full text]
  • Autocovariance Function Estimation Via Penalized Regression
    Autocovariance Function Estimation via Penalized Regression Lina Liao, Cheolwoo Park Department of Statistics, University of Georgia, Athens, GA 30602, USA Jan Hannig Department of Statistics and Operations Research, University of North Carolina, Chapel Hill, NC 27599, USA Kee-Hoon Kang Department of Statistics, Hankuk University of Foreign Studies, Yongin, 449-791, Korea Abstract The work revisits the autocovariance function estimation, a fundamental problem in statistical inference for time series. We convert the function estimation problem into constrained penalized regression with a generalized penalty that provides us with flexible and accurate estimation, and study the asymptotic properties of the proposed estimator. In case of a nonzero mean time series, we apply a penalized regression technique to a differenced time series, which does not require a separate detrending procedure. In penalized regression, selection of tuning parameters is critical and we propose four different data-driven criteria to determine them. A simulation study shows effectiveness of the tuning parameter selection and that the proposed approach is superior to three existing methods. We also briefly discuss the extension of the proposed approach to interval-valued time series. Some key words: Autocovariance function; Differenced time series; Regularization; Time series; Tuning parameter selection. 1 1 Introduction Let fYt; t 2 T g be a stochastic process such that V ar(Yt) < 1, for all t 2 T . The autoco- variance function of fYtg is given as γ(s; t) = Cov(Ys;Yt) for all s; t 2 T . In this work, we consider a regularly sampled time series f(i; Yi); i = 1; ··· ; ng. Its model can be written as Yi = g(i) + i; i = 1; : : : ; n; (1.1) where g is a smooth deterministic function and the error is assumed to be a weakly stationary 2 process with E(i) = 0, V ar(i) = σ and Cov(i; j) = γ(ji − jj) for all i; j = 1; : : : ; n: The estimation of the autocovariance function γ (or autocorrelation function) is crucial to determine the degree of serial correlation in a time series.
    [Show full text]
  • LECTURES 2 - 3 : Stochastic Processes, Autocorrelation Function
    LECTURES 2 - 3 : Stochastic Processes, Autocorrelation function. Stationarity. Important points of Lecture 1: A time series fXtg is a series of observations taken sequentially over time: xt is an observation recorded at a specific time t. Characteristics of times series data: observations are dependent, become available at equally spaced time points and are time-ordered. This is a discrete time series. The purposes of time series analysis are to model and to predict or forecast future values of a series based on the history of that series. 2.2 Some descriptive techniques. (Based on [BD] x1.3 and x1.4) ......................................................................................... Take a step backwards: how do we describe a r.v. or a random vector? ² for a r.v. X: 2 d.f. FX (x) := P (X · x), mean ¹ = EX and variance σ = V ar(X). ² for a r.vector (X1;X2): joint d.f. FX1;X2 (x1; x2) := P (X1 · x1;X2 · x2), marginal d.f.FX1 (x1) := P (X1 · x1) ´ FX1;X2 (x1; 1) 2 2 mean vector (¹1; ¹2) = (EX1; EX2), variances σ1 = V ar(X1); σ2 = V ar(X2), and covariance Cov(X1;X2) = E(X1 ¡ ¹1)(X2 ¡ ¹2) ´ E(X1X2) ¡ ¹1¹2. Often we use correlation = normalized covariance: Cor(X1;X2) = Cov(X1;X2)=fσ1σ2g ......................................................................................... To describe a process X1;X2;::: we define (i) Def. Distribution function: (fi-di) d.f. Ft1:::tn (x1; : : : ; xn) = P (Xt1 · x1;:::;Xtn · xn); i.e. this is the joint d.f. for the vector (Xt1 ;:::;Xtn ). (ii) First- and Second-order moments. ² Mean: ¹X (t) = EXt 2 2 2 2 ² Variance: σX (t) = E(Xt ¡ ¹X (t)) ´ EXt ¡ ¹X (t) 1 ² Autocovariance function: γX (t; s) = Cov(Xt;Xs) = E[(Xt ¡ ¹X (t))(Xs ¡ ¹X (s))] ´ E(XtXs) ¡ ¹X (t)¹X (s) (Note: this is an infinite matrix).
    [Show full text]
  • A University of Sussex Phd Thesis Available Online Via Sussex
    A University of Sussex PhD thesis Available online via Sussex Research Online: http://sro.sussex.ac.uk/ This thesis is protected by copyright which belongs to the author. This thesis cannot be reproduced or quoted extensively from without first obtaining permission in writing from the Author The content must not be changed in any way or sold commercially in any format or medium without the formal permission of the Author When referring to this work, full bibliographic details including the author, title, awarding institution and date of the thesis must be given Please visit Sussex Research Online for more information and further details NON-STATIONARY PROCESSES AND THEIR APPLICATION TO FINANCIAL HIGH-FREQUENCY DATA Mailan Trinh A thesis submitted for the degree of Doctor of Philosophy University of Sussex March 2018 UNIVERSITY OF SUSSEX MAILAN TRINH A THESIS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY NON-STATIONARY PROCESSES AND THEIR APPLICATION TO FINANCIAL HIGH-FREQUENCY DATA SUMMARY The thesis is devoted to non-stationary point process models as generalizations of the standard homogeneous Poisson process. The work can be divided in two parts. In the first part, we introduce a fractional non-homogeneous Poisson process (FNPP) by applying a random time change to the standard Poisson process. We character- ize the FNPP by deriving its non-local governing equation. We further compute moments and covariance of the process and discuss the distribution of the arrival times. Moreover, we give both finite-dimensional and functional limit theorems for the FNPP and the corresponding fractional non-homogeneous compound Poisson process. The limit theorems are derived by using martingale methods, regular vari- ation properties and Anscombe's theorem.
    [Show full text]
  • Regularity of Solutions and Parameter Estimation for Spde’S with Space-Time White Noise
    REGULARITY OF SOLUTIONS AND PARAMETER ESTIMATION FOR SPDE’S WITH SPACE-TIME WHITE NOISE by Igor Cialenco A Dissertation Presented to the FACULTY OF THE GRADUATE SCHOOL UNIVERSITY OF SOUTHERN CALIFORNIA In Partial Fulfillment of the Requirements for the Degree DOCTOR OF PHILOSOPHY (APPLIED MATHEMATICS) May 2007 Copyright 2007 Igor Cialenco Dedication To my wife Angela, and my parents. ii Acknowledgements I would like to acknowledge my academic adviser Prof. Sergey V. Lototsky who introduced me into the Theory of Stochastic Partial Differential Equations, suggested the interesting topics of research and guided me through it. I also wish to thank the members of my committee - Prof. Remigijus Mikulevicius and Prof. Aris Protopapadakis, for their help and support. Last but certainly not least, I want to thank my wife Angela, and my family for their support both during the thesis and before it. iii Table of Contents Dedication ii Acknowledgements iii List of Tables v List of Figures vi Abstract vii Chapter 1: Introduction 1 1.1 Sobolev spaces . 1 1.2 Diffusion processes and absolute continuity of their measures . 4 1.3 Stochastic partial differential equations and their applications . 7 1.4 Ito’sˆ formula in Hilbert space . 14 1.5 Existence and uniqueness of solution . 18 Chapter 2: Regularity of solution 23 2.1 Introduction . 23 2.2 Equations with additive noise . 29 2.2.1 Existence and uniqueness . 29 2.2.2 Regularity in space . 33 2.2.3 Regularity in time . 38 2.3 Equations with multiplicative noise . 41 2.3.1 Existence and uniqueness . 41 2.3.2 Regularity in space and time .
    [Show full text]
  • Variance Function Regressions for Studying Inequality
    Variance Function Regressions for Studying Inequality The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Western, Bruce and Deirdre Bloome. 2009. Variance function regressions for studying inequality. Working paper, Department of Sociology, Harvard University. Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:2645469 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Open Access Policy Articles, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#OAP Variance Function Regressions for Studying Inequality Bruce Western1 Deirdre Bloome Harvard University January 2009 1Department of Sociology, 33 Kirkland Street, Cambridge MA 02138. E-mail: [email protected]. This research was supported by a grant from the Russell Sage Foundation. Abstract Regression-based studies of inequality model only between-group differ- ences, yet often these differences are far exceeded by residual inequality. Residual inequality is usually attributed to measurement error or the in- fluence of unobserved characteristics. We present a regression that in- cludes covariates for both the mean and variance of a dependent variable. In this model, the residual variance is treated as a target for analysis. In analyses of inequality, the residual variance might be interpreted as mea- suring risk or insecurity. Variance function regressions are illustrated in an analysis of panel data on earnings among released prisoners in the Na- tional Longitudinal Survey of Youth. We extend the model to a decomposi- tion analysis, relating the change in inequality to compositional changes in the population and changes in coefficients for the mean and variance.
    [Show full text]