DOCSLIB.ORG

Geometry Notes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry Notes Geometry Notes Paul Yiu Department of Mathematics Florida Atlantic University July 31, 2004 Contents 1 Triangle centers 1 1.1 December 1, 1999: X500 ........................... 1 1.2 May 20, 2000: Orthocentroidal circle . ................... 2 1.2.1 The Evans conic . .......................... 5 1.2.2 The type of the Evans conic . ................... 5 1.2.3 . ................................. 7 1.3 January 13, 2001: The bridge points . ................... 8 1.4 October 24, 2001 . .......................... 10 1.5 November 19, 2001: Tatiana Emelyanov on the Feuerbach point . 12 1.6 December 12, 2001: Edward Brisses’ construction of the Steiner point . 15 1.7 March 19, 2002: Taylor center . ................... 16 1.8 May 9, 2002: On X184 ............................ 16 1.9 ........................................ 16 1.10 May 11, 2002: Points on cubic . ................... 17 1.11 November 28, 2002 . .......................... 17 1.12 January 3, 2003: Bogomolny’s conjecture . ............ 18 1.13 January 22, 2003: Nikolaos Dergiades’ problem . ............ 19 1.14 February 26, 2003: Arnold’s Theorem ................... 20 1.15 March 5, 2003: Coordinates of the foci of Steiner in-ellipse ........ 21 1.16 March 12, 2003: Lev Emelyanov . ................... 21 1.16.1 March 14, 2003 . .......................... 22 1.17 March 13, 2003: David Wilson on X647 ................... 23 1.18 March 15, 2003: Malfatti-Rabinowitz points . ............ 23 1.19 June 8, 2003: ................................. 24 1.20 June 14, 2003: Steiner point and the nine-point center . ........ 24 1.21 September 29, 2003: APH and ED . ................... 24 1.22 October, 25, 2003: X1337 and X1338 ..................... 25 1.23 November 3, 2003: Eric Danneels . ................... 25 1.24 November 6, 2003 . .......................... 26 1.25 November 11, 2003: X1113 and X1822 .................... 26 1.26 December 1, 2003: JPE on two Lemoine centers . ............ 27 1.27 December 3, 2003: Darij Grinberg on generalization of orthocenter . 28 1.28 December 8, 2003: . .......................... 28 1.29 January 6, 2004: Eric Danneels . ................... 29 iv CONTENTS 1.30 January 20, 2004: Darij Grinberg’s Mittenpunkt note . ...... 29 1.31 February 11, 2004 . ........................ 29 1.32 February 14, 2004: Barycentric cube of Euler infinite point . ...... 29 1.33 February 26, 2004: Eric Danneels . ................. 30 1.34 March 19, 2004: Discrepancies with ETC ................. 30 1.35 March 21, 2004: X2028 and X2029 ...................... 31 1.36 March 22, 2004: Eric Daaneels . ................. 32 1.37 March 23, 2004: ............................... 33 1.37.1 JPE, Hyacinthos 6333, corrected in Hyacinthos 6337 . ...... 33 1.37.2 DG, Hyacinthos 7164 . ........................ 34 1.38 April 3, 2004: . ............................... 34 1.39 April 7, 2004: . ............................... 34 1.40 April 14, 2004: (Hyacinthos 9687) Symmedian point of the Apollonius triangle . ............................... 34 1.41 May 12, 2004: X57 = perspector of orthic triangle of intouch triangle . 35 1.42 May 28, 2004: ETC description of X552 and X553 ............. 35 1.43 June 2, 2004: Symmedian point . ................. 36 1.44 July 1, 2004: Edward Brisse on X(557) .................. 36 1.45 July 2, 2004: Eric Danneels . ........................ 36 1.46 July 16, 2004: Stevanovic . ........................ 37 1.47 July 17, 2004: X1157 ............................. 39 1.48 July 17, 2004: The deLongchamps point . ................. 39 1.49 July 21, 2004: APH on eight circumcenters ................. 40 1.50 July 24, 2004: Circumcenters tangential and Kosnita triangle . ...... 41 1.51 July 24, 2004: . ............................... 41 2 Homothetic triangles 43 2.1 March 11, 2000: Two Pairs of Poristic Conics Associated with parallel intercepts . ............................... 43 2.1.1 The conic CP ............................. 43 2.1.2 The center of the conic CP ...................... 44 2.1.3 The conic inscribed in the hexagon W (P ) .............. 45 2.1.4 Another hexagon AC BACB .................... 46 2.1.5 Examples ............................... 47 2.2 March 18, 2000: A quadruple of homothetic triangles with four collinear centers of similitude . ........................ 48 2.3 March 21, 2000: Homothetic Centers . ................. 51 2.3.1 The Euler and Carnot triangles . ................. 52 2.4 April 8, 2004: . ............................... 53 2.5 July 24, 2004: Gob homothetic center . ................. 54 3 Parallelians 55 3.1 March 9, 2000: Lemoine’s Problem . ................. 55 3.2 January 18, 2002: Parallelian Hyacinthos 4667 . ............. 57 3.3 June 19, 2002: Conic through the endpoints of parallelians through P ... 59 CONTENTS v 3.4 September 6, 2002: Parallelians . ................... 60 4 Pedal triangles 61 4.1 January 5, 2001: Perspectivity of pedal triangle and anticevian triangle . 61 4.2 August 31, 2002: Pedal residuals . ................... 61 4.3 June 2, 2004: Pedal triangle . ................... 61 4.3.1 A variation . .......................... 62 5 Operations 63 5.1 October 16, 1999: APH’s product . ................... 63 5.2 April 5, 2000: Harmon of desmic systems . ............ 66 5.3 October 24, 2001 . .......................... 68 5.4 October 27, 2001 . .......................... 70 5.5 February 18, 2002: Isoscelizers . ................... 71 5.6 October 26, 2002: Orthogonal quadrisection of a triangle . ........ 72 5.7 January 22, 2003: Euler’s quadrisection problem . ............ 72 5.8 January 24, 2003: Darij Grinberg’s isotome complement . ........ 73 5.9 February 13, 2003: Myakishev’s cevasix note . ............ 74 5.10 March 6, 2003: Isoscelizers . ................... 74 5.11 March 9, 2003: Left and right isoscelizers . ............ 78 5.12 October 24, 2003: Bernard’s AOC paper . ............ 79 5.13 November 4, 2003: . .......................... 81 5.13.1 . ................................. 81 5.14 November 8, 2003: The barycentric cube of an infinite point ........ 82 5.15 November 14, 2003: APH’s symmetrologic triangles ............ 82 5.16 November 15, 2003: Euler quartic . ................... 83 5.17 November 19, 2003: Paper from Turkey . ............ 84 5.18 November 23, 2003: Intersections of circles and lines . ........ 87 5.19 December 4, 2003: Least square line . ................... 88 5.20 February 6, 2004: APH circumcevian triangle problem . ........ 88 5.21 April 5, 2004: An interesting distance formula . ............ 89 5.22 April 19, Abu-Saymeh and Hajji . ................... 89 5.23 April 28, 2004: Isogonal conjugate of the inferior . ............ 89 5.24 June 2, 2004: JPE’s Hyacinthos 10000 ................... 89 5.25 June 10, 2004: Michel Garitte . ................... 90 5.26 July 29, 2004: APH’s second and third orthocorrespondences . 90 6 Euler lines 93 6.1 January 22, 2004: . .......................... 93 6.2 January 28, 2004: Final touches on the concurrent Euler lines paper . 94 6.3 January 30, 2004 . .......................... 97 6.4 July 25, 2004: Euler line . .......................... 97 vi CONTENTS 7 Residuals 99 7.1 November 20, 2002: Mario Dalc´in..................... 99 7.2 December 3, 2002: Mario Dalcin . ................. 99 8 Orthology 101 8.1 May 20, 2004: Orthology . ........................101 8.2 May 26, 2004: orthology . ........................102 8.3 June 4, 2004: APH, Hyacinthos 9858 . .................102 8.3.1 A variation . ........................102 8.4 July 11, 2004: . ...............................102 8.5 July 27, 2004: JPE on orthologic triangles .................102 8.6 July 30, 2004: JPE on orthology centers . .................104 9 Transformation of coordinates 105 9.1 May 17, 2002: Transformation of coordinates . .............105 9.1.1 McCay cubic with reference to the excentral triangle . ......105 10 Cevian nests 107 10.1 February 28, 2002: FvL, Hyacinthos 4839 .................107 10.2 September 15, 2003: The cevian nest theorem . .............108 10.3 March 18 2004: Cevian quotients . .................109 10.3.1 G/P .................................109 10.3.2 H/P .................................109 10.4 March 26, 2004: ...............................110 11 Reflections 113 11.1 October 19, 1999: Musselman’s theorem . .................113 11.2 December 9, 2000: Reflections . .................115 11.3 September 28, 2001: Reflection triangle . .................121 11.4 Gilles Bouttes, Hyacinthos 3997 (9/28/01) .................123 11.5 October 26, 2001: Reflection triangles . .................123 11.6 June 1, 2002: Scimemi’s paper . .................125 11.7 August 9, 2002. Paper folding the roots of a cubic equation . ......127 11.8 January 18, 2003: Musselman’s 1940 Monthly paper . ......129 11.9 March 1, 2003: Reflections . ........................130 11.10 September 24, 2003: JPE on reflections of a point in its cevian triangle . 131 11.11 December 30, 2003: Hatzipolakis reflection point X1986 ..........132 11.12 December 31, 2003: Reflections of circumcircles of pedal residuals . 133 11.13 January 8, 2004: D. Moody Bailey . .................135 11.14 January 31, 2004: . ........................135 11.15 February 9, 2004: . ........................136 11.16 February 17, 2004: Reflections in altitudes .................136 11.17 February 17, 2004: . ........................137 11.18 March 18, 2004: Reflection conjugates . .................138 11.19 March 26, 2004: Review on Simson and reflection lines . ......138 CONTENTS vii 11.19.1 Simson lines of antipodal points ...................139
Load more

Recommended publications
  • Investigating Centers of Triangles: the Fermat Point
    Investigating Centers of Triangles: The Fermat Point A thesis submitted to the Miami University Honors Program in partial fulfillment of the requirements for University Honors with Distinction by Katherine Elizabeth Strauss May 2011 Oxford, Ohio ABSTRACT INVESTIGATING CENTERS OF TRIANGLES: THE FERMAT POINT By Katherine Elizabeth Strauss Somewhere along their journey through their math classes, many students develop a fear of mathematics. They begin to view their math courses as the study of tricks and often seemingly unsolvable puzzles. There is a demand for teachers to make mathematics more useful and believable by providing their students with problems applicable to life outside of the classroom with the intention of building upon the mathematics content taught in the classroom. This paper discusses how to integrate one specific problem, involving the Fermat Point, into a high school geometry curriculum. It also calls educators to integrate interesting and challenging problems into the mathematics classes they teach. In doing so, a teacher may show their students how to apply the mathematics skills taught in the classroom to solve problems that, at first, may not seem directly applicable to mathematics. The purpose of this paper is to inspire other educators to pursue similar problems and investigations in the classroom in order to help students view mathematics through a more useful lens. After a discussion of the Fermat Point, this paper takes the reader on a brief tour of other useful centers of a triangle to provide future researchers and educators a starting point in order to create relevant problems for their students. iii iv Acknowledgements First of all, thank you to my advisor, Dr.
    [Show full text]
  • Configurations on Centers of Bankoff Circles 11
    CONFIGURATIONS ON CENTERS OF BANKOFF CIRCLES ZVONKO CERINˇ Abstract. We study configurations built from centers of Bankoff circles of arbelos erected on sides of a given triangle or on sides of various related triangles. 1. Introduction For points X and Y in the plane and a positive real number λ, let Z be the point on the segment XY such that XZ : ZY = λ and let ζ = ζ(X; Y; λ) be the figure formed by three mj utuallyj j tangenj t semicircles σ, σ1, and σ2 on the same side of segments XY , XZ, and ZY respectively. Let S, S1, S2 be centers of σ, σ1, σ2. Let W denote the intersection of σ with the perpendicular to XY at the point Z. The figure ζ is called the arbelos or the shoemaker's knife (see Fig. 1). σ σ1 σ2 PSfrag replacements X S1 S Z S2 Y XZ Figure 1. The arbelos ζ = ζ(X; Y; λ), where λ = jZY j . j j It has been the subject of studies since Greek times when Archimedes proved the existence of the circles !1 = !1(ζ) and !2 = !2(ζ) of equal radius such that !1 touches σ, σ1, and ZW while !2 touches σ, σ2, and ZW (see Fig. 2). 1991 Mathematics Subject Classification. Primary 51N20, 51M04, Secondary 14A25, 14Q05. Key words and phrases. arbelos, Bankoff circle, triangle, central point, Brocard triangle, homologic. 1 2 ZVONKO CERINˇ σ W !1 σ1 !2 W1 PSfrag replacements W2 σ2 X S1 S Z S2 Y Figure 2. The Archimedean circles !1 and !2 together.
    [Show full text]
  • Cevians, Symmedians, and Excircles Cevian Cevian Triangle & Circle
    10/5/2011 Cevians, Symmedians, and Excircles MA 341 – Topics in Geometry Lecture 16 Cevian A cevian is a line segment which joins a vertex of a triangle with a point on the opposite side (or its extension). B cevian C A D 05-Oct-2011 MA 341 001 2 Cevian Triangle & Circle • Pick P in the interior of ∆ABC • Draw cevians from each vertex through P to the opposite side • Gives set of three intersecting cevians AA’, BB’, and CC’ with respect to that point. • The triangle ∆A’B’C’ is known as the cevian triangle of ∆ABC with respect to P • Circumcircle of ∆A’B’C’ is known as the evian circle with respect to P. 05-Oct-2011 MA 341 001 3 1 10/5/2011 Cevian circle Cevian triangle 05-Oct-2011 MA 341 001 4 Cevians In ∆ABC examples of cevians are: medians – cevian point = G perpendicular bisectors – cevian point = O angle bisectors – cevian point = I (incenter) altitudes – cevian point = H Ceva’s Theorem deals with concurrence of any set of cevians. 05-Oct-2011 MA 341 001 5 Gergonne Point In ∆ABC find the incircle and points of tangency of incircle with sides of ∆ABC. Known as contact triangle 05-Oct-2011 MA 341 001 6 2 10/5/2011 Gergonne Point These cevians are concurrent! Why? Recall that AE=AF, BD=BF, and CD=CE Ge 05-Oct-2011 MA 341 001 7 Gergonne Point The point is called the Gergonne point, Ge. Ge 05-Oct-2011 MA 341 001 8 Gergonne Point Draw lines parallel to sides of contact triangle through Ge.
    [Show full text]
  • Kaleidoscopic Symmetries and Self-Similarity of Integral Apollonian Gaskets
    Kaleidoscopic Symmetries and Self-Similarity of Integral Apollonian Gaskets Indubala I Satija Department of Physics, George Mason University , Fairfax, VA 22030, USA (Dated: April 28, 2021) Abstract We describe various kaleidoscopic and self-similar aspects of the integral Apollonian gaskets - fractals consisting of close packing of circles with integer curvatures. Self-similar recursive structure of the whole gasket is shown to be encoded in transformations that forms the modular group SL(2;Z). The asymptotic scalings of curvatures of the circles are given by a special set of quadratic irrationals with continued fraction [n + 1 : 1; n] - that is a set of irrationals with period-2 continued fraction consisting of 1 and another integer n. Belonging to the class n = 2, there exists a nested set of self-similar kaleidoscopic patterns that exhibit three-fold symmetry. Furthermore, the even n hierarchy is found to mimic the recursive structure of the tree that generates all Pythagorean triplets arXiv:2104.13198v1 [math.GM] 21 Apr 2021 1 Integral Apollonian gaskets(IAG)[1] such as those shown in figure (1) consist of close packing of circles of integer curvatures (reciprocal of the radii), where every circle is tangent to three others. These are fractals where the whole gasket is like a kaleidoscope reflected again and again through an infinite collection of curved mirrors that encodes fascinating geometrical and number theoretical concepts[2]. The central themes of this paper are the kaleidoscopic and self-similar recursive properties described within the framework of Mobius¨ transformations that maps circles to circles[3]. FIG. 1: Integral Apollonian gaskets.
    [Show full text]
  • Control Point Based Representation of Inellipses of Triangles∗
    Annales Mathematicae et Informaticae 40 (2012) pp. 37–46 http://ami.ektf.hu Control point based representation of inellipses of triangles∗ Imre Juhász Department of Descriptive Geometry, University of Miskolc, Hungary [email protected] Submitted April 12, 2012 — Accepted May 20, 2012 Abstract We provide a control point based parametric description of inellipses of triangles, where the control points are the vertices of the triangle themselves. We also show, how to convert remarkable inellipses defined by their Brianchon point to control point based description. Keywords: inellipse, cyclic basis, rational trigonometric curve, Brianchon point MSC: 65D17, 68U07 1. Introduction It is well known from elementary projective geometry that there is a two-parameter family of ellipses that are within a given non-degenerate triangle and touch its three sides. Such ellipses can easily be constructed in the traditional way (by means of ruler and compasses), or their implicit equation can be determined. We provide a method using which one can determine the parametric form of these ellipses in a fairly simple way. Nowadays, in Computer Aided Geometric Design (CAGD) curves are repre- sented mainly in the form n g (u) = j=0 Fj (u) dj δ Fj :[a, b] R, u [a, b] R, dj R , δ 2 P→ ∈ ⊂ ∈ ≥ ∗This research was carried out as a part of the TAMOP-4.2.1.B-10/2/KONV-2010-0001 project with support by the European Union, co-financed by the European Social Fund. 37 38 I. Juhász where dj are called control points and Fj (u) are blending functions. (The most well-known blending functions are Bernstein polynomials and normalized B-spline basis functions, cf.
    [Show full text]
  • Automated Study of Isoptic Curves: a New Approach with Geogebra∗
    Automated study of isoptic curves: a new approach with GeoGebra∗ Thierry Dana-Picard1 and Zoltan Kov´acs2 1 Jerusalem College of Technology, Israel [email protected] 2 Private University College of Education of the Diocese of Linz, Austria [email protected] March 7, 2018 Let C be a plane curve. For a given angle θ such that 0 ≤ θ ≤ 180◦, a θ-isoptic curve of C is the geometric locus of points in the plane through which pass a pair of tangents making an angle of θ.If θ = 90◦, the isoptic curve is called the orthoptic curve of C. For example, the orthoptic curves of conic sections are respectively the directrix of a parabola, the director circle of an ellipse, and the director circle of a hyperbola (in this case, its existence depends on the eccentricity of the hyperbola). Orthoptics and θ-isoptics can be studied for other curves than conics, in particular for closed smooth strictly convex curves,as in [1]. An example of the study of isoptics of a non-convex non-smooth curve, namely the isoptics of an astroid are studied in [2] and of Fermat curves in [3]. The Isoptics of an astroid present special properties: • There exist points through which pass 3 tangents to C, and two of them are perpendicular. • The isoptic curve are actually union of disjoint arcs. In Figure 1, the loops correspond to θ = 120◦ and the arcs connecting them correspond to θ = 60◦. Such a situation has been encountered already for isoptics of hyperbolas. These works combine geometrical experimentation with a Dynamical Geometry System (DGS) GeoGebra and algebraic computations with a Computer Algebra System (CAS).
    [Show full text]
  • Strophoids, a Family of Cubic Curves with Remarkable Properties
    Hellmuth STACHEL STROPHOIDS, A FAMILY OF CUBIC CURVES WITH REMARKABLE PROPERTIES Abstract: Strophoids are circular cubic curves which have a node with orthogonal tangents. These rational curves are characterized by a series or properties, and they show up as locus of points at various geometric problems in the Euclidean plane: Strophoids are pedal curves of parabolas if the corresponding pole lies on the parabola’s directrix, and they are inverse to equilateral hyperbolas. Strophoids are focal curves of particular pencils of conics. Moreover, the locus of points where tangents through a given point contact the conics of a confocal family is a strophoid. In descriptive geometry, strophoids appear as perspective views of particular curves of intersection, e.g., of Viviani’s curve. Bricard’s flexible octahedra of type 3 admit two flat poses; and here, after fixing two opposite vertices, strophoids are the locus for the four remaining vertices. In plane kinematics they are the circle-point curves, i.e., the locus of points whose trajectories have instantaneously a stationary curvature. Moreover, they are projections of the spherical and hyperbolic analogues. For any given triangle ABC, the equicevian cubics are strophoids, i.e., the locus of points for which two of the three cevians have the same lengths. On each strophoid there is a symmetric relation of points, so-called ‘associated’ points, with a series of properties: The lines connecting associated points P and P’ are tangent of the negative pedal curve. Tangents at associated points intersect at a point which again lies on the cubic. For all pairs (P, P’) of associated points, the midpoints lie on a line through the node N.
    [Show full text]
  • The Vertex-Midpoint-Centroid Triangles
    Forum Geometricorum b Volume 4 (2004) 97–109. bbb FORUM GEOM ISSN 1534-1178 The Vertex-Midpoint-Centroid Triangles Zvonko Cerinˇ Abstract. This paper explores six triangles that have a vertex, a midpoint of a side, and the centroid of the base triangle ABC as vertices. They have many in- teresting properties and here we study how they monitor the shape of ABC. Our results show that certain geometric properties of these six triangles are equivalent to ABC being either equilateral or isosceles. Let A, B, C be midpoints of the sides BC, CA, AB of the triangle ABC and − let G be its centroid (i.e., the intersection of medians AA, BB , CC ). Let Ga , + − + − + Ga , Gb , Gb , Gc , Gc be triangles BGA , CGA , CGB , AGB , AGC , BGC (see Figure 1). C − + Gb Ga B A G + − Gb Ga − + Gc Gc ABC Figure 1. Six vertex–midpoint–centroid triangles of ABC. This set of six triangles associated to the triangle ABC is a special case of the cevasix configuration (see [5] and [7]) when the chosen point is the centroid G.It has the following peculiar property (see [1]). Theorem 1. The triangle ABC is equilateral if and only if any three of the trian- = { − + − + − +} gles from the set σG Ga ,Ga ,Gb ,Gb ,Gc ,Gc have the same either perime- ter or inradius. In this paper we wish to show several similar results. The idea is to replace perimeter and inradius with other geometric notions (like k-perimeter and Brocard angle) and to use various central points (like the circumcenter and the orthocenter – see [4]) of these six triangles.
    [Show full text]
  • HYPERBOLA HYPERBOLA a Conic Is Said to Be a Hyperbola If Its Eccentricity Is Greater Than One
    HYPERBOLA HYPERBOLA A Conic is said to be a hyperbola if its eccentricity is greater than one. If S ax22 hxy by 2 2 gx 2 fy c 0 represents a hyperbola then h2 ab 0 and 0 2 2 If S ax2 hxy by 2 gx 2 fy c 0 represents a rectangular hyperbola then h2 ab 0 , 0 and a b 0 x2 y 2 Hyperbola: Equation of the hyperbola in standard form is 1. a2 b2 Hyperbola is symmetric about both the axes. Hyperbola does not passing through the origin and does not meet the Y - axis. Hyperbola curve does not exist between the lines x a and x a . x2 y 2 xx yy x2 y 2 x x y y Notation: S 1 , S1 1 1, S1 1 1, S1 2 1 2 1. a2 b 2 1 a2 b 2 11 a2 b 2 12 a2 b 2 Rectangular hyperbola (or) Equilateral hyperbola : In a hyperbola if the length of the transverse axis (2a) is equal to the length of the conjugate axis (2b) , then the hyperbola is called a rectangular hyperbola or an equilateral hyperbola. The eccentricity of a rectangular hyperbola is 2 . Conjugate hyperbola : The hyperbola whose transverse and conjugate axes are respectively the conjugate and transverse axes of a given hyperbola is called the conjugate hyperbola of the given hyperbola. 2 2 1 x y The equation of the hyperbola conjugate to S 0 is S 1 0 . a2 b 2 If e1 and e2 be the eccentricities of the hyperbola and its conjugate hyperbola then 1 1 2 2 1.
    [Show full text]
  • Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points arXiv:2101.02592v1 [math.HO] 6 Jan 2021 in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron.
    [Show full text]
  • A Special Conic Associated with the Reuleaux Negative Pedal Curve
    INTERNATIONAL JOURNAL OF GEOMETRY Vol. 10 (2021), No. 2, 33–49 A SPECIAL CONIC ASSOCIATED WITH THE REULEAUX NEGATIVE PEDAL CURVE LILIANA GABRIELA GHEORGHE and DAN REZNIK Abstract. The Negative Pedal Curve of the Reuleaux Triangle w.r. to a pedal point M located on its boundary consists of two elliptic arcs and a point P0. Intriguingly, the conic passing through the four arc endpoints and by P0 has one focus at M. We provide a synthetic proof for this fact using Poncelet’s porism, polar duality and inversive techniques. Additional interesting properties of the Reuleaux negative pedal w.r. to pedal point M are also included. 1. Introduction Figure 1. The sides of the Reuleaux Triangle R are three circular arcs of circles centered at each Reuleaux vertex Vi; i = 1; 2; 3. of an equilateral triangle. The Reuleaux triangle R is the convex curve formed by the arcs of three circles of equal radii r centered on the vertices V1;V2;V3 of an equilateral triangle and that mutually intercepts in these vertices; see Figure1. This triangle is mostly known due to its constant width property [4]. Keywords and phrases: conic, inversion, pole, polar, dual curve, negative pedal curve. (2020)Mathematics Subject Classification: 51M04,51M15, 51A05. Received: 19.08.2020. In revised form: 26.01.2021. Accepted: 08.10.2020 34 Liliana Gabriela Gheorghe and Dan Reznik Figure 2. The negative pedal curve N of the Reuleaux Triangle R w.r. to a point M on its boundary consist on an point P0 (the antipedal of M through V3) and two elliptic arcs A1A2 and B1B2 (green and blue).
    [Show full text]
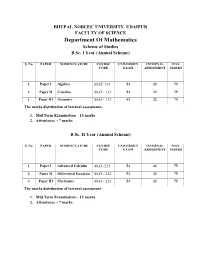
  • Department of Mathematics Scheme of Studies B.Sc
    BHUPAL NOBLES` UNIVERSITY, UDAIPUR FACULTY OF SCIENCE Department Of Mathematics Scheme of Studies B.Sc. I Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Algebra MAT-111 53 22 75 2. Paper II Calculus MAT- 112 53 22 75 3. Paper III Geometry MAT- 113 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. II Year (Annual Scheme) S. No. PAPER NOMENCLATURE COURSE UNIVERSITY INTERNAL MAX. CODE EXAM ASSESSMENT MARKS 1. Paper I Advanced Calculus MAT-221 53 22 75 2. Paper II Differential Equation MAT- 222 53 22 75 3. Paper III Mechanics MAT- 223 53 22 75 The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks B.Sc. III Year (Annual Scheme) S. PAPER NOMENCLATURE COURSE CODE UNIVERSITY INTERNAL MAX. No. EXAM ASSESSMENT MARKS 1. Paper I Real Analysis MAT-331 53 22 75 2. Paper II Advanced Algebra MAT- 332 53 22 75 3. Paper Numerical Analysis MAT-333 (A) 53 22 75 III Mathematical MAT-333 (B) Quantitative Techniques Mathematical MAT-333 (C) Statistics The marks distribution of internal assessment- 1. Mid Term Examination – 15 marks 2. Attendance – 7 marks BHUPAL NOBLES’ UNIVERSITY, UDAIPUR Department of Mathematics Syllabus 2017 -2018 (COMMON FOR THE FACULTIES OF ARTS & SCIENCE) B.A. / B. Sc. FIRST YEAR EXAMINATIONS 2017-2020 MATHEMATICS Theory Papers Name Papers Code Papers Maximum Papers hours/ Marks BA/ week B.Sc. Paper I ALGEBRA MAT-111 3 75 Paper II CALCULUS MAT-112 3 75 Paper III GEOMETRY MAT-113 3 75 Total Marks 225 NOTE: 1.
    [Show full text]