Squaring a Frame, Version 3.0
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Extra Long Screwdriver Bits Kit Box Tool Holders
EXTRA LONG PHILLIPS® EXTRA LONG BITS 150MM 150mm long Phillips® screwdriver bits in three SCREWDRIVER BITS sizes No.1, 2 and 3. Bit Size Order Ref. Price EXTRA LONG TORX® EXTRA LONG POZI® Phillips® No. 1 SNAP/PH/1A £5.00 BITS 150MM BITS 150MM Phillips® No. 2 SNAP/PH/2A £5.00 Phillips® No. 3 SNAP/PH/3A £5.00 150mm long Torx® screw driver bits with round 150mm long Pozi® Screwdriver bits in three shafts. Can be used with T-Star® screws. sizes No.1, 2 and 3. EXTRA LONG Bit Size Machine Screw Order Ref. Price Bit Size Order Ref. Price SQUARE DRIVE BITS ® ® Torx T10 M3 SNAP/TX/10A £5.00 Pozi No. 1 SNAP/PZ/1A £5.00 Two lengths of No.2 Robertson square drive Torx® T15 M3.5 SNAP/TX/15A £5.00 Pozi® No. 2 SNAP/PZ/2A £5.00 bits. 75mm (3”) and 150mm (6”) for use with Torx® T20 M4 SNAP/TX/20A £5.00 Pozi® No. 3 SNAP/PZ/3A £6.00 Pocket Hole Jig. Torx® T25 M5 SNAP/TX/25A £5.00 Bit Size Order Ref. Price Torx® T30 M6 SNAP/TX/30A £5.00 Robertson® No. 2 (3”) SNAP/SQ/2A £4.00 Robertson® No. 2 (6”) SNAP/SQ/2B £5.00 KIT BOX 19 PIECE METRIC KIT BOX Standard Quick Chuck 1, 2, 3, 4, 5, 7 and 7mm drills. No.6, 8 and 10 drill bit guide. No. 4, 6, 8, 10 and 12 drill countersinks and Pozi® No.1, 2 and 3 50mm screwdriver bits. -

1. Hand Tools 3. Related Tools 4. Chisels 5. Hammer 6. Saw Terminology 7. Pliers Introduction
1 1. Hand Tools 2. Types 2.1 Hand tools 2.2 Hammer Drill 2.3 Rotary hammer drill 2.4 Cordless drills 2.5 Drill press 2.6 Geared head drill 2.7 Radial arm drill 2.8 Mill drill 3. Related tools 4. Chisels 4.1. Types 4.1.1 Woodworking chisels 4.1.1.1 Lathe tools 4.2 Metalworking chisels 4.2.1 Cold chisel 4.2.2 Hardy chisel 4.3 Stone chisels 4.4 Masonry chisels 4.4.1 Joint chisel 5. Hammer 5.1 Basic design and variations 5.2 The physics of hammering 5.2.1 Hammer as a force amplifier 5.2.2 Effect of the head's mass 5.2.3 Effect of the handle 5.3 War hammers 5.4 Symbolic hammers 6. Saw terminology 6.1 Types of saws 6.1.1 Hand saws 6.1.2. Back saws 6.1.3 Mechanically powered saws 6.1.4. Circular blade saws 6.1.5. Reciprocating blade saws 6.1.6..Continuous band 6.2. Types of saw blades and the cuts they make 6.3. Materials used for saws 7. Pliers Introduction 7.1. Design 7.2.Common types 7.2.1 Gripping pliers (used to improve grip) 7.2 2.Cutting pliers (used to sever or pinch off) 2 7.2.3 Crimping pliers 7.2.4 Rotational pliers 8. Common wrenches / spanners 8.1 Other general wrenches / spanners 8.2. Spe cialized wrenches / spanners 8.3. Spanners in popular culture 9. Hacksaw, surface plate, surface gauge, , vee-block, files 10. -

Punching Tools
TruServices Punching Tools Order easily – with the correct specifica- tions for the right tool. Have you thought of everything? Machine type Machine number Tool type Dimensions or drawings in a conventional CAD format (e.g. DXF) Sheet thickness Material Quantity Desired delivery date Important ordering specifications ! Please observe the "Important ordering specifications" on each product page as well. Order your punching tools securely and conveniently 24 hours a day, 7 days a week in our E-Shop at: www.trumpf.com/mytrumpf Alternatively, practical inquiry and order forms are available to you in the chapter "Order forms". TRUMPF Werkzeugmaschinen GmbH + Co. KG International Sales Punching Tools Hermann-Dreher-Strasse 20 70839 Gerlingen Germany E-mail: [email protected] Homepage: www.trumpf.com Content Order easily – with the correct specifica- General information tions for the right tool. TRUMPF System All-round Service Industry 4.0 MyTRUMPF 4 Have you thought of everything? Machine type Punching Machine number Classic System MultiTool Tool type Cluster tools MultiUse Dimensions or drawings in a conventional CAD format (e.g. DXF) 12 Sheet thickness Material Cutting Quantity Slitting tool Film slitting tool Desired delivery date MultiShear 44 Important ordering specifications ! Please observe the "Important ordering specifications" on each product page as well. Forming Countersink tool Thread forming tool Extrusion tool Cup tool 58 Marking Order your punching tools securely and conveniently 24 hours a day, 7 days a week in our E-Shop at: Center punch tool Marking tool Engraving tool Embossing tool www.trumpf.com/mytrumpf 100 Alternatively, practical inquiry and order forms are available to you in the chapter "Order forms". -

Chisel Quilts
1501 Easy Chisel Quilts REQUIRED GO! Baby Friendly Twelve Star Quilt Quilt 49” x 61” Finished Block SizeSize 11½”11½” Teresa Varnes Amie Potter Long Braid Tablee RunneRunnerr 14” x 102” Finished Width ooff BrBraidaid 6” Eleanor Burns Judy Jackson Medium Length Braid Table Runner 14” x 54” 2 Select from a Star Lap Robe or Braid Table Runer in two sizes featuring AccuQuilt® Die #55039 for Chisels. The Star also uses Die #55009 for Half Square Triangles. This die is #3 from the 6” Mix and Match series. The Chisel die cuts two shapes at a time. Chisels #55039 The Half Square Half Square Triangle Triangle die cuts four #55009 shapes at a time. Carefully follow cutting instructions, because they are not the same for both projects. Chisels for Star Lap Robe are cut from strips placed right side up. Chisels for Braid Table Runner are cut from strips placed wrong sides together in pairs. 3 Fabric Selection Decide on the theme or era of your projects, such as Civil War, Depression, Traditional, Modern, Juvenile, or Holiday. It's easy to select from a line that a designer put together in a variety of prints and solids, or ones that appear solid. A total of eighteen fat quar- ters is enough for both projects, including two Table Runners in the medium length. Select twelve medium to dark print fat quarters in a variety of values, colors, and scales. Select six Background prints in similar values but different textures that appear solid and do not distract from prints. Twelve Fat Quarters Six Backgrounds In additional, purchase fabric listed on page 5 for finishing your project. -

Bandsaw Puzzle Cubes
Bandsaw Puzzle Cubes How’s that scrap pile in the corner of the shop coming along? Getting any smaller? Here’s one way to put some of your cherished chunks of thick stock to good use, producing casual gifts of irresistible appeal to young and old alike. Kids under ten can reassemble these puzzles in 30 seconds, grown-ups in only three or four minutes if they’re sharp. Make sure your bandsaw blade is square to the table, both left & right and fore & aft. The larger the puzzle cube, the less error you can get away with. Kerf width forgives some inaccuracy, but not much. Start off by milling up a cube — any size will do, but bigger is bet- ter: 3” x 3” or 4” x 4” makes a good puzzle blank. Put a 1/8” or 1/16” blade on your bandsaw, and don’t think about any claims you might have seen that you can’t cut thick stock with a very nar- row blade. Cool Blocks™ lateral guides are essential for 1/16”s and mighty useful for controlling 1/8” blades, too. Orient the cube so you’ll start cut- ting across the grain, and cut a ran- domly invented jigsaw puzzle pattern across the block. Make a fairly simple pattern. Push gently, using just your fingertips. Let the saw take its time working throughthe stock, so the blade stays vertical and your curves are consistent throughout.You’ll notice that sawing with the grain is much slower than across it; be ready for significant changes in speed and back pressure as you turn the block. -

Magnetic Tip Tape Measures
malco tool book | better ideas for the real world. Magnetic Tip Tape Measures Magnetic Attraction! At last, the obvious! Malco’s “Magnetic Tip” tape measure is ideal for every ferrous metalworking project! Use it for HVAC ductwork installations, ceiling grid applications, metal stud framing and more. A powerful magnet and self-supporting 1” wide blade makes Powerful Magnets! Ideal for working with metal! 1-person measurements and measuring elevations an easy task. The magnetic tip and big standout blade can even be used as a Zero Commencement: pick-up tool! A double riveted tip connection, abrasion-resistant, When Hanging and pulling magnet, nylon coated blade and rubber-clad housing and blade stop assure deduct 1/16” from measurement. lasting performance. T416M T425M A MULTITUDE OF JOB SITE USES: Metal Ductwork | Ceiling Grids T430M | Metal Stud Framing Measuring Elevations | One-Person Measurements | Extended blade tip even works as pick-up tool! Non-Magnetic Tape Measures • Non Magnetic 1” Tape Measures • Double Riveted Tip Connection • Rubber-Clad Housing CT430 CT425 Specifications Catalog Net Wt. Number Description oz. (g) T416M 1” x 16’ Magnetic Tip Tape Measure 10 (284) T425M 1” x 25’ Magnetic Tip Tape Measure 14 (397) T430M 1” x 30’ Magnetic Tip Tape Measure 17 (482) CT425 1” x 25’ Tape Measure 13 (369) CT430 1” x 30’ Tape Measure 16 (454) 122 Malco Products Inc. Est. 1950 malco tool book | www.malcotools.com 48AR Aluminum Straight Edge Rule Made from .125 thickness extruded aluminum. This 48” rule is 2” wide. Large and clear, easy to read, thermo-bonded red markings on gray finish. -

Vertical Panel Saws Innovative Carts
Vertical Panel Innovative Saws Carts ANYTHING OTHER THAN A SAW TRAX JUST DOESN’T CUT IT... SAW TRAX CARTS DOLLY MAX ALL TERRAIN yel-Low DOLLY SERIES VARIABLE LOADING HEIGHT PANEL EXPRESS SELF ADJUSTING SCOOP DOLLY REPLACES FORKLIFT WE DIDN’T REINVENT THE WHEEL, JUST THE DOLLY... Vertical Panel Saws Product Description: The Basic Series panel saws include only the standard equipment (see below) and Basic are ideal for cost-conscious customers. A Universal Saw Insert Plate is provided, so SERIES the user can mount nearly any 7 ¼ inch circular saw and can be inserted vertical- ly or horizontally. This series is ideal for customers that need to break down full size sheet goods that are less than 1¾ inches thick. Although basic, this panel saw model can be enhanced. Want to use a router or a utility knife in this unit? You can add a Floating Router Insert Plate or a Pivoting Universal Saw Insert Plate Knife Cutter Insert. Choose from the optional Wall Mount Kit or optional COMPACT Folding Stand for even more versatility! Our unique Accu-Glide sealed roller bearing system provides for smoother carriage action and tighter tolerances. Available Compact Model: 52” Cross Cut Model# C52B MSRP: $1399 Sealed Steel Roller Bearings Available Full Size Model: 64” Cross Cut Model# FS64B MSRP: $2399 FULL SIZE Standard Equipment: Package Includes: Optional Accessories: Patented Alignment System Powder Coated Steel Frame Saw not included Folding Stand 11 Gauge Steel Guide Tubes Universal Saw Insert Plate Transport Wheels Accu-Glide Sealed Bearing System Full Mid-Fence Quick Release Carriage System Floating Router Insert Plate Retraction Mechanism Wall Mounting System Cord Holder Full Builder’s Extensions Center Support Step Laser Pointer Rip Pointers Our patented Accu-Square alignment system assures that your Stop Bar machine will never go out of square. -

The Starrett Combination Square Introduction, Assembly & Applications Congratulations on Your Purchase of a Starrett Combinaton Square
Applications: Combination Square Center Head The Starrett Combination Square Introduction, Assembly & Applications Congratulations on your purchase of a Starrett Combinaton Square. Starrett was the first and is still the best combination square available. Invented by our Laroy S. Starrett, in 1877, the combination square was literally the driving force in the founding of The L.S. Starrett Company in 1880. After more than 130 years, this practical and versatile tool is still commonly utilized in a wide variety of applications. Laroy S. Starrett (1836-1922) Applications: Combination Square Protractor Head Description and Components The combination square includes a hardened steel graduated rule and movable combination square and miter head with spirit level and scriber. The square head has a precision ground 90° square face and a 45° miter face. It is a highly versatile layout tool for scribing right angles and parallel lines, and a measuring tool that can be used as a tri-square, miter, depth gage, height gage, and level. The Center Head is an available attachment that provides an easy means of accurately locating the center of cylindrical or square work. The Protractor Head is another available attachment. It has revolving turrets with direct-reading double graduations, a full 0 to 180° in opposite directions. This permits accurate and quick direct reading of angles above or below the blade. Complete Sets are available including the rule and all three heads in a fitted case. Tips for Using Squares and Center Heads Scriber • Ensure that the square is clean and located against a flat surface – irregularities Spirit Level (Reverse Side) such as burrs on metal or knots on wood adversely effect accuracy. -

3/8" Magnetic Corner Chisel 50S01.01
3/8" Magnetic Corner Chisel 50S01.01 The Veritas® Magnetic Corner Chisel is designed for squaring off the corners of routed hinge gains. The 3/8" square chisel is guided by the anodized aluminum guide block containing two embedded rare-earth magnets. The chisel is made from A2 tool steel hardened to Rc60 and comes honed with a 35° bevel on each face. Guide Block Chisel Instructions Figure 1: The corner chisel. Though it can be used on its own, greater accuracy is ensured by use of the 2" tall guide block. Its two rare-earth magnets hold the chisel square, while the outside faces of the block register against the routed pocket. Slide the corner chisel into the routed corner, with the body against the end and side of the pocket. Hold in position and tap the top of the chisel with a hammer. The Hinge Gain result is perfectly located square score marks. The routed corner can then be pared with a chisel, producing a neat, square corner. Figure 2: Cutting corners. Resharpening You will come to appreciate the fine edge that the chisel came with and the long-wearing properties of A2 tool steel once you finally have to resharpen it, as sharpening corner chisels is never an easy task! The difficulty lies in honing the two cutting edges right into the corner while keeping both edges straight and at 90° to the chisel. This is best done using a fine hone that has abrasive only on a single face (most diamond hones are made this way). -

ICS Wood Boring Tools Catalog
REVISED OCT 2020 ICS CUTTING TOOLS, INC 511 Main Street • Casco, WI 54205-0125 USA (920) 837-2526 • Fax (920) 837-2530 www.icscuttingtools.com • [email protected] TABLE OF CONTENTS Auger Bits Drills Dual Auger (Stud) ............................................................19 Brad Point Hand Drive Screw Eye ....................................................28 1/2" Shank ..................................................................14 Impact Wrench 3/8" Shank ..................................................................10 Quick Change Hex Shank ............................................26 Straight Shank .............................................................10 Square Socket (Female) ..............................................28 Pipe .................................................................................23 Center Drills .................................................................17 SDS Shank ......................................................................28 Machine Drills - 1/2" Shank .......................................12 Ship Auger Multi-Angle Drills ...........................................................6 6" Length .....................................................................24 Silver & Deming Drills - 1/2" Shank - Brad Point ........11 8" Length .....................................................................24 Drill Point Center Drills ...................................................18 18" Length ...................................................................24 -

Sawing Basics V63WCWO3 Operator Variables That Aid Sawing Performance When Making Blade Recommendations, There Are a Few Questions We Need to Answer
Sawing Basics V63WCWO3 Operator Variables That Aid Sawing Performance When making blade recommendations, there are a few questions we need to answer: • Which blade do we use? • Which tooth pitch do we use? • Which blade speed should we use? • Which feed rate should we use? • What is the relationship between feed & speed? • Why do we need a cutting fluid? • Why do we need blade break‐in? Which blade do we use? Items that influence selection • Machine type—Low cost, low performance machines will not allow a band saw blade to function optimally. • For low performance machines, select blades that can withstand higher shock, chatter, or • The better the feed system on a machine, the higher performance blade that can be used effectively. • Production Rate– The more cuts per hour or the longer the run time the higher the performance blades will be needed. • Cost Per Cut‐To lower the cost per cut, move to a higher performance blade. What Blade Do We Use? Items That Influence Selection Material Machinability‐ Machinability is generally rated from 0 to 100% (SAE1112, rated at 100%, is considered free cutting) • Alloy type (Carbon vs. Nickel‐based, etc.), hardness (Heat‐Treated or aged), and material shape all affect material machinability • The higher the alloy, the lower the machinability rating • The higher the material hardness, the lower the machinability • Complex material shapes will lower the machinability rating due to increase shock Abrasiveness‐ Abrasive material or coatings will reduce the life of a band saw blade‐ consider carbide tipped -
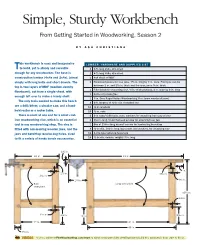
Simple, Sturdy Workbench from Getting Started in Woodworking, Season 2
Simple, Sturdy Workbench From Getting Started in Woodworking, Season 2 BY ASA CHRISTIANA his workbench is easy and inexpensive LUMBER, HARDWARE AND SUPPLIES LIST Tto build, yet is sturdy and versatile 4 8-ft.-long 2x4s, kiln-dried enough for any woodworker. The base is 2 8-ft.-long 4x4s, kiln-dried construction lumber (4x4s and 2x4s), joined 1 4x8 sheet of MDF simply with long bolts and short dowels. The 2 Hardwood pieces for vise jaws, 71/2 in. long by 3 in. wide. Front jaw can be top is two layers of MDF (medium-density between 1 in. and 11/2 in. thick and the rear jaw is 3/4 in. thick. 1 Filler block for mounting vise, 3/4-in.-thick plywood, 4 in. wide by 6 in. long fiberboard), cut from a single sheet, with 1 bottle of yellow glue enough left over to make a handy shelf. 1 7-in. Groz Rapid-Action Woodworking Vise (www.woodcraft.com) The only tools needed to make this bench 4 6-ft. lengths of 3⁄8-in.-dia. threaded rod are a drill/driver, a circular saw, and a hand- 16 3⁄8-in. washers held router or a router table. 16 3⁄8-in. nuts There is room at one end for a small cast- 2 2-in.-long 1/4-20 bolts, nuts, washers for attaching front jaw of vise iron woodworking vise, which is an essential 2 11/2-in.-long, 1/4-20 flathead screws for attaching rear jaw tool in any woodworking shop.