Using Asteroseismology to Characterise Exoplanet Host Stars
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Exomoon Habitability Constrained by Illumination and Tidal Heating
submitted to Astrobiology: April 6, 2012 accepted by Astrobiology: September 8, 2012 published in Astrobiology: January 24, 2013 this updated draft: October 30, 2013 doi:10.1089/ast.2012.0859 Exomoon habitability constrained by illumination and tidal heating René HellerI , Rory BarnesII,III I Leibniz-Institute for Astrophysics Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany, [email protected] II Astronomy Department, University of Washington, Box 951580, Seattle, WA 98195, [email protected] III NASA Astrobiology Institute – Virtual Planetary Laboratory Lead Team, USA Abstract The detection of moons orbiting extrasolar planets (“exomoons”) has now become feasible. Once they are discovered in the circumstellar habitable zone, questions about their habitability will emerge. Exomoons are likely to be tidally locked to their planet and hence experience days much shorter than their orbital period around the star and have seasons, all of which works in favor of habitability. These satellites can receive more illumination per area than their host planets, as the planet reflects stellar light and emits thermal photons. On the contrary, eclipses can significantly alter local climates on exomoons by reducing stellar illumination. In addition to radiative heating, tidal heating can be very large on exomoons, possibly even large enough for sterilization. We identify combinations of physical and orbital parameters for which radiative and tidal heating are strong enough to trigger a runaway greenhouse. By analogy with the circumstellar habitable zone, these constraints define a circumplanetary “habitable edge”. We apply our model to hypothetical moons around the recently discovered exoplanet Kepler-22b and the giant planet candidate KOI211.01 and describe, for the first time, the orbits of habitable exomoons. -

BRAS Newsletter August 2013
www.brastro.org August 2013 Next meeting Aug 12th 7:00PM at the HRPO Dark Site Observing Dates: Primary on Aug. 3rd, Secondary on Aug. 10th Photo credit: Saturn taken on 20” OGS + Orion Starshoot - Ben Toman 1 What's in this issue: PRESIDENT'S MESSAGE....................................................................................................................3 NOTES FROM THE VICE PRESIDENT ............................................................................................4 MESSAGE FROM THE HRPO …....................................................................................................5 MONTHLY OBSERVING NOTES ....................................................................................................6 OUTREACH CHAIRPERSON’S NOTES .........................................................................................13 MEMBERSHIP APPLICATION .......................................................................................................14 2 PRESIDENT'S MESSAGE Hi Everyone, I hope you’ve been having a great Summer so far and had luck beating the heat as much as possible. The weather sure hasn’t been cooperative for observing, though! First I have a pretty cool announcement. Thanks to the efforts of club member Walt Cooney, there are 5 newly named asteroids in the sky. (53256) Sinitiere - Named for former BRAS Treasurer Bob Sinitiere (74439) Brenden - Named for founding member Craig Brenden (85878) Guzik - Named for LSU professor T. Greg Guzik (101722) Pursell - Named for founding member Wally Pursell -

The Ubvri and Infrared Colour Indices of the Sun and Sun-Like Stars
The 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun Edited by G. A. Feiden THE UBVRI AND INFRARED COLOUR INDICES OF THE SUN AND SUN-LIKE STARS Mehmet TANRIVER1, Ferhat Fikri ÖZEREN1 1 Erciyes University, Astronomy and Space Sciences Department, 38039, Kayseri, Turkey Abstract The Sun is not a point source, the photometric observational techniques that are utilised for observing other stars cannot be utilised for the Sun, meaning that it is dicult to derive its colours accurately for astronomical work from direct measurements in dierent passbands. The solar twins are the best choices because they are the stars that are ideally the same as the Sun in all parameters, and also, their colours are highly similar to those of the Sun. From the 60 articles on the Sun and Sun-like stars in the literature from 1964 until today, the solar colour indices in the optic and infrared regions have been estimated. 1 INTRODUCTION Table 1: The obtained average colour indices values of the The Sun is an average-low-mass star in the main sequence Sun with standart deviation (±σ)( Tanrıver (2012), Tanrıver of the Hertzsprung-Russell diagram. Moreover, the Sun is (2014a), Tanrıver (2014b) ). not a point source, the photometric observational techniques that are utilised for observing other stars cannot be utilised B-V 0.6457 ± 0.0421 V-J 1.1413 ± 0.1063 for the Sun. Therefore, the colours and colour indices of the H-K 0.0572 ± 0.0351 U-B 0.1463 ± 0.0596 sun-like stars are used in order to determine the sun’s colour V-H 1.4613 ± 0.1183 J-K 0.3777 ± 0.0494 indices. -

Multiple Star Systems Observed with Corot and Kepler
Multiple star systems observed with CoRoT and Kepler John Southworth Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK Abstract. The CoRoT and Kepler satellites were the first space platforms designed to perform high-precision photometry for a large number of stars. Multiple systems dis- play a wide variety of photometric variability, making them natural benefactors of these missions. I review the work arising from CoRoT and Kepler observations of multiple sys- tems, with particular emphasis on eclipsing binaries containing giant stars, pulsators, triple eclipses and/or low-mass stars. Many more results remain untapped in the data archives of these missions, and the future holds the promise of K2, TESS and PLATO. 1 Introduction The CoRoT and Kepler satellites represent the first generation of astronomical space missions capable of large-scale photometric surveys. The large quantity – and exquisite quality – of the data they pro- vided is in the process of revolutionising stellar and planetary astrophysics. In this review I highlight the immense variety of the scientific results from these concurrent missions, as well as the context provided by their precursors and implications for their successors. CoRoT was led by CNES and ESA, launched on 2006/12/27,and retired in June 2013 after an irre- trievable computer failure in November 2012. It performed 24 observing runs, each lasting between 21 and 152days, with a field of viewof 2×1.3◦ ×1.3◦, obtaining light curves of 163000 stars [42]. Kepler was a NASA mission, launched on 2009/03/07and suffering a critical pointing failure on 2013/05/11. It observed the same 105deg2 sky area for its full mission duration, obtaining high-precision light curves of approximately 191000 stars. -

Magnetism, Dynamo Action and the Solar-Stellar Connection
Living Rev. Sol. Phys. (2017) 14:4 DOI 10.1007/s41116-017-0007-8 REVIEW ARTICLE Magnetism, dynamo action and the solar-stellar connection Allan Sacha Brun1 · Matthew K. Browning2 Received: 23 August 2016 / Accepted: 28 July 2017 © The Author(s) 2017. This article is an open access publication Abstract The Sun and other stars are magnetic: magnetism pervades their interiors and affects their evolution in a variety of ways. In the Sun, both the fields themselves and their influence on other phenomena can be uncovered in exquisite detail, but these observations sample only a moment in a single star’s life. By turning to observa- tions of other stars, and to theory and simulation, we may infer other aspects of the magnetism—e.g., its dependence on stellar age, mass, or rotation rate—that would be invisible from close study of the Sun alone. Here, we review observations and theory of magnetism in the Sun and other stars, with a partial focus on the “Solar-stellar connec- tion”: i.e., ways in which studies of other stars have influenced our understanding of the Sun and vice versa. We briefly review techniques by which magnetic fields can be measured (or their presence otherwise inferred) in stars, and then highlight some key observational findings uncovered by such measurements, focusing (in many cases) on those that offer particularly direct constraints on theories of how the fields are built and maintained. We turn then to a discussion of how the fields arise in different objects: first, we summarize some essential elements of convection and dynamo theory, includ- ing a very brief discussion of mean-field theory and related concepts. -

Habitability on Local, Galactic and Cosmological Scales
Habitability on local, Galactic and cosmological scales Luigi Secco1 • Marco Fecchio1 • Francesco Marzari1 Abstract The aim of this paper is to underline con- detectable studying our site. The Climatic Astronom- ditions necessary for the emergence and development ical Theory is introduced in sect.5 in order to define of life. They are placed at local planetary scale, at the circumsolar habitable zone (HZ) (sect.6) while the Galactic scale and within the cosmological evolution, translation from Solar to extra-Solar systems leads to a as pointed out by the Anthropic Cosmological Princi- generalized circumstellar habitable zone (CHZ) defined ple. We will consider the circumstellar habitable zone in sect.7 with some exemplifications to the Gliese-667C (CHZ) for planetary systems and a Galactic Habitable and the TRAPPIST-1 systems; some general remarks Zone (GHZ) including also a set of strong cosmologi- follow (sect.8). A first conclusion related to CHZ is cal constraints to allow life (cosmological habitability done moving toward GHZ and COSH (sect.9). The (COSH)). Some requirements are specific of a single conditions for the development of life are indeed only scale and its related physical phenomena, while others partially connected to the local scale in which a planet are due to the conspired effects occurring at more than is located. A strong interplay between different scales one scale. The scenario emerging from this analysis is exists and each single contribution to life from individ- that all the habitability conditions here detailed must ual scales is difficult to be isolated. However we will at least be met. -

___... -.:: GEOCITIES.Ws
__ __ _____ _____ _____ _____ ____ _ __ / / / / /_ _/ / ___/ /_ _/ / __ ) / _ \ | | / / / /__/ / / / ( ( / / / / / / / /_) / | |/ / / ___ / / / \ \ / / / / / / / _ _/ | _/ / / / / __/ / ____) ) / / / /_/ / / / \ \ / / /_/ /_/ /____/ /_____/ /_/ (_____/ /_/ /_/ /_/ _____ _____ _____ __ __ _____ / __ ) / ___/ /_ _/ / / / / / ___/ / / / / / /__ / / / /__/ / / /__ / / / / / ___/ / / / ___ / / ___/ / /_/ / / / / / / / / / / /___ (_____/ /_/ /_/ /_/ /_/ /_____/ _____ __ __ _____ __ __ ____ _____ / ___/ / / / / /_ _/ / / / / / _ \ / ___/ / /__ / / / / / / / / / / / /_) / / /__ / ___/ / / / / / / / / / / / _ _/ / ___/ / / / /_/ / / / / /_/ / / / \ \ / /___ /_/ (_____/ /_/ (_____/ /_/ /_/ /_____/ A TIMELINE OF THE MULTIVERSE Version 1.21 By K. Bradley Washburn "The Historian" ______________ | __ | | \| /\ / | | |/_/ / | | |\ \/\ / | | |_\/ \/ | |______________| K. Bradley Washburn HISTORY OF THE FUTURE Page 2 of 2 FOREWARD Relevant Notes WARNING: THIS FILE IS HAZARDOUS TO YOUR PRINTER'S INK SUPPLY!!! [*Story(Time Before:Time Transpired:Time After)] KEY TO ABBREVIATIONS AS--The Amazing Stories AST--Animated Star Trek B5--Babylon 5 BT--The Best of Trek DS9--Deep Space Nine EL--Enterprise Logs ENT--Enterprise LD--The Lives of Dax NE--New Earth NF--New Frontier RPG--Role-Playing Games S.C.E.--Starfleet Corps of Engineers SA--Starfleet Academy SNW--Strange New Worlds sQ--seaQuest ST--Star Trek TNG--The Next Generation TNV--The New Voyages V--Voyager WLB—Gateways: What Lay Beyond Blue italics - Completely canonical. Animated and live-action movies, episodes, and their novelizations. Green italics - Officially canonical. Novels, comics, and graphic novels. Red italics – Marginally canonical. Role-playing material, source books, internet sources. For more notes, see the AFTERWORD K. Bradley Washburn HISTORY OF THE FUTURE Page 3 of 3 TIMELINE circa 13.5 billion years ago * The Big Bang. -

A Basic Requirement for Studying the Heavens Is Determining Where In
Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short). -

The Maunder Minimum and the Variable Sun-Earth Connection
The Maunder Minimum and the Variable Sun-Earth Connection (Front illustration: the Sun without spots, July 27, 1954) By Willie Wei-Hock Soon and Steven H. Yaskell To Soon Gim-Chuan, Chua Chiew-See, Pham Than (Lien+Van’s mother) and Ulla and Anna In Memory of Miriam Fuchs (baba Gil’s mother)---W.H.S. In Memory of Andrew Hoff---S.H.Y. To interrupt His Yellow Plan The Sun does not allow Caprices of the Atmosphere – And even when the Snow Heaves Balls of Specks, like Vicious Boy Directly in His Eye – Does not so much as turn His Head Busy with Majesty – ‘Tis His to stimulate the Earth And magnetize the Sea - And bind Astronomy, in place, Yet Any passing by Would deem Ourselves – the busier As the Minutest Bee That rides – emits a Thunder – A Bomb – to justify Emily Dickinson (poem 224. c. 1862) Since people are by nature poorly equipped to register any but short-term changes, it is not surprising that we fail to notice slower changes in either climate or the sun. John A. Eddy, The New Solar Physics (1977-78) Foreword By E. N. Parker In this time of global warming we are impelled by both the anticipated dire consequences and by scientific curiosity to investigate the factors that drive the climate. Climate has fluctuated strongly and abruptly in the past, with ice ages and interglacial warming as the long term extremes. Historical research in the last decades has shown short term climatic transients to be a frequent occurrence, often imposing disastrous hardship on the afflicted human populations. -
![Arxiv:2010.13762V1 [Astro-Ph.EP] 26 Oct 2020](https://docslib.b-cdn.net/cover/3118/arxiv-2010-13762v1-astro-ph-ep-26-oct-2020-523118.webp)
Arxiv:2010.13762V1 [Astro-Ph.EP] 26 Oct 2020
Draft version October 27, 2020 Typeset using LATEX default style in AASTeX63 A Framework for Relative Biosignature Yields from Future Direct Imaging Missions Noah W. Tuchow 1 and Jason T. Wright 1 1Department of Astronomy & Astrophysics and Center for Exoplanets and Habitable Worlds and Penn State Extraterrestrial Intelligence Center 525 Davey Laboratory The Pennsylvania State University University Park, PA, 16802, USA ABSTRACT Future exoplanet direct imaging missions, such as HabEx and LUVOIR, will select target stars to maximize the number of Earth-like exoplanets that can have their atmospheric compositions charac- terized. Because one of these missions' aims is to detect biosignatures, they should also consider the expected biosignature yield of planets around these stars. In this work, we develop a method of computing relative biosignature yields among potential target stars, given a model of habitability and biosignature genesis, and using a star's habitability history. As an illustration and first application of this method, we use MESA stellar models to calculate the time evolution of the habitable zone, and examine three simple models for biosignature genesis to calculate the relative biosignature yield for different stars. We find that the relative merits of K stars versus F stars depend sensitively on model choice. In particular, use of the present-day habitable zone as a proxy for biosignature detectability favors young, luminous stars lacking the potential for long-term habitability. Biosignature yields are also sensitive to whether life can arise on Cold Start exoplanets that enter the habitable zone after formation, an open question deserving of more attention. Using the case study of biosignature yields calculated for θ Cygni and 55 Cancri, we find that robust mission design and target selection for HabEx and LUVOIR depends on: choosing a specific model of biosignature appearance with time; the terrestrial planet occurrence rate as a function of orbital separation; precise knowledge of stellar properties; and accurate stellar evolutionary histories. -
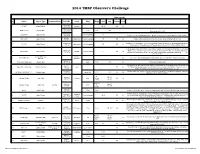
2014 Observers Challenge List
2014 TMSP Observer's Challenge Atlas page #s # Object Object Type Common Name RA, DEC Const Mag Mag.2 Size Sep. U2000 PSA 18h31m25s 1 IC 1287 Bright Nebula Scutum 20'.0 295 67 -10°47'45" 18h31m25s SAO 161569 Double Star 5.77 9.31 12.3” -10°47'45" Near center of IC 1287 18h33m28s NGC 6649 Open Cluster 8.9m Integrated 5' -10°24'10" Can be seen in 3/4d FOV with above. Brightest star is 13.2m. Approx 50 stars visible in Binos 18h28m 2 NGC 6633 Open Cluster Ophiuchus 4.6m integrated 27' 205 65 Visible in Binos and is about the size of a full Moon, brightest star is 7.6m +06°34' 17h46m18s 2x diameter of a full Moon. Try to view this cluster with your naked eye, binos, and a small scope. 3 IC 4665 Open Cluster Ophiuchus 4.2m Integrated 60' 203 65 +05º 43' Also check out “Tweedle-dee and Tweedle-dum to the east (IC 4756 and NGC 6633) A loose open cluster with a faint concentration of stars in a rich field, contains about 15-20 stars. 19h53m27s Brightest star is 9.8m, 5 stars 9-11m, remainder about 12-13m. This is a challenge obJect to 4 Harvard 20 Open Cluster Sagitta 7.7m integrated 6' 162 64 +18°19'12" improve your observation skills. Can you locate the miniature coathanger close by at 19h 37m 27s +19d? Constellation star Corona 5 Corona Borealis 55 Trace the 7 stars making up this constellation, observe and list the colors of each star asterism Borealis 15H 32' 55” Theta Corona Borealis Double Star 4.2m 6.6m .97” 55 Theta requires about 200x +31° 21' 32” The direction our Sun travels in our galaxy. -

Exoplanet Community Report
JPL Publication 09‐3 Exoplanet Community Report Edited by: P. R. Lawson, W. A. Traub and S. C. Unwin National Aeronautics and Space Administration Jet Propulsion Laboratory California Institute of Technology Pasadena, California March 2009 The work described in this publication was performed at a number of organizations, including the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (NASA). Publication was provided by the Jet Propulsion Laboratory. Compiling and publication support was provided by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not constitute or imply its endorsement by the United States Government, or the Jet Propulsion Laboratory, California Institute of Technology. © 2009. All rights reserved. The exoplanet community’s top priority is that a line of probeclass missions for exoplanets be established, leading to a flagship mission at the earliest opportunity. iii Contents 1 EXECUTIVE SUMMARY.................................................................................................................. 1 1.1 INTRODUCTION...............................................................................................................................................1 1.2 EXOPLANET FORUM 2008: THE PROCESS OF CONSENSUS BEGINS.....................................................2