Efficient Unbiased Rendering of Thin Participating Media
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017
ENGINEERING SOFTWARE DEVELOPMENT MADE EASY Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017 www.amcbridge.com Cloud Renderer for Autodesk Revit User Guide Contents Contents .................................................................................................................................................... 2 Welcome to Cloud Renderer for Autodesk Revit ...................................................................................... 3 Requirements and Installation .................................................................................................................. 5 Functionality.............................................................................................................................................. 8 Cloud Renderer Plug-in ......................................................................................................................... 8 Basic Settings ..................................................................................................................................... 8 Advanced Settings ........................................................................................................................... 10 Session manager ............................................................................................................................. 15 Single session view .......................................................................................................................... 17 Cloud Renderer on Microsoft® Azure® platfrom ............................................................................... -
3D Rendering Software Free Download Full Version Download 3 D Rendering - Best Software & Apps
3d rendering software free download full version Download 3 D Rendering - Best Software & Apps. NVIDIA Control Panel is a Windows utility tool, which lets users access critical functions of the NVIDIA drivers. With a comprehensive set of dropdown menus. OpenGL. An open-source graphics library. OpenGL is an open-source graphics standard for generating vector graphics in 2D as well as 3D. The cross-language Windows application has numerous functions. Autodesk Maya. Powerful 3D modeling, animation and rendering solution. Autodesk Maya is a highly professional solution for 3D modeling, animation and rendering in one complete and very powerful package.It has won several awards. Bring Your Models To Life With Powerful Rendering Tools. V-Ray is 3D model rendering software, usable with many different modelling programs but particularly compatible with SketchUp, Maya, Blender and others for. Envisioneer Express. Free 3D home design tool. Envisioneer Express is a multimedia application from Cadsoft. It is a free graphic design program that allows users to create plans for any residential. Virtual Lab. Discover the micro world with this virtual microscope. I was always fascinated by the science laboratory hours at school, when we had to use microscopes to literally discover new words, and test chemical. An extremely powerful 3D animation tool. modo has long been the application of choice for animation studios like Pixar Studios and Industrial Light and Magic. The latest update to modo improves upon. Voyager - Buy Bitcoin Crypto. A free program for Android, by Voyager Digital LLC. Voyager is a free software for Android, that belongs to the category 'Finance'. -

Indigo Manual
Contents Overview.............................................................................................4 About Indigo Renderer...........................................................................5 Licensing Indigo...................................................................................9 Indigo Licence activation......................................................................11 System Requirements..........................................................................14 About Installation................................................................................16 Installation on Windows.......................................................................17 Installation on Macintosh......................................................................19 Installation on Linux............................................................................20 Installing exporters for your modelling package........................................21 Working with the Indigo Interface Getting to know Indigo........................................................................23 Resolution.........................................................................................28 Tone Mapping.....................................................................................29 White balance....................................................................................36 Light Layers.......................................................................................37 Aperture Diffraction.............................................................................39 -

Probabilistic Connections for Bidirectional Path Tracing
Eurographics Symposium on Rendering 2015 Volume 34 (2015), Number 4 J. Lehtinen and D. Nowrouzezahrai (Guest Editors) Probabilistic Connections for Bidirectional Path Tracing Stefan Popov 1 Ravi Ramamoorthi 2 Fredo Durand 3 George Drettakis 1 1 Inria 2 UC San Diego 3 MIT CSAIL Bidirectional Path Tracing Probabilistic Connections for Bidirectional Path Tracing Figure 1: Our Probabilistic Connections for Bidirectional Path Tracing approach importance samples connections to an eye sub-path, and greatly reduces variance, by considering and reusing multiple light sub-paths at once. Our approach (right) achieves much higher quality than bidirectional path-tracing on the left for the same computation time (~8.4 min). Abstract Bidirectional path tracing (BDPT) with Multiple Importance Sampling is one of the most versatile unbiased ren- dering algorithms today. BDPT repeatedly generates sub-paths from the eye and the lights, which are connected for each pixel and then discarded. Unfortunately, many such bidirectional connections turn out to have low con- tribution to the solution. Our key observation is that we can importance sample connections to an eye sub-path by considering multiple light sub-paths at once and creating connections probabilistically. We do this by storing light paths, and estimating probability mass functions of the discrete set of possible connections to all light paths. This has two key advantages: we efficiently create connections with low variance by Monte Carlo sampling, and we reuse light paths across different eye paths. We also introduce a caching scheme by deriving an approxima- tion to sub-path contribution which avoids high-dimensional path distance computations. Our approach builds on caching methods developed in the different context of VPLs. -
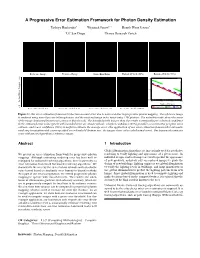
A Progressive Error Estimation Framework for Photon Density Estimation
A Progressive Error Estimation Framework for Photon Density Estimation Toshiya Hachisuka∗ Wojciech Jaroszy;∗ Henrik Wann Jensen∗ ∗UC San Diego yDisney Research Zurich¨ Reference Image Rendered Image Noise/Bias Ratio Bounded Pixels (50%) Bounded Pixels (90%) 5 . 0 1.0 s e g a m I 0.1 r o r r E l a u t c 0.01 10 100 1000 8000 A Number of Iterations 0 . 0 actual error 90% 50% Error Threshold: 0.5 Error Threshold: 0.25 Error Threshold: 0.125 Error Threshold: 0.0625 Figure 1: Our error estimation framework takes into account error due to noise and bias in progressive photon mapping. The reference image is rendered using more than one billion photons, and the rendered image is the result using 15M photons. The noise/bias ratio shows the areas of the image dominated by noise (in green) or bias (in red). The bounded pixels images show the results corresponding to a desired confidence in the estimated error value (pixels with bounded error are shown yellow): a higher confidence (90%) provides a conservative per pixel error estimate, and lower confidence (50%) is useful to estimate the average error. One application of our error estimation framework is automatic rendering termination with a user-specified error threshold (bottom row: the images show color-coded actual error). Our framework estimates error without any input from a reference image. Abstract 1 Introduction Global illumination algorithms are increasingly used for predictive We present an error estimation framework for progressive photon rendering to verify lighting and appearance of a given scene. -

Reweighting Firefly Samples for Improved Finite-Sample Monte
Volume xx (200y), Number z, pp. 1–10 Reweighting Firefly Samples for Improved Finite-Sample Monte Carlo Estimates Tobias Zirr, Johannes Hanika, and Carsten Dachsbacher Karlsruhe Institute of Technology Abstract Samples with high contribution but low probability density, often called fireflies, occur in all practical Monte Carlo estima- tors and are part of computing unbiased estimates. For finite-sample estimates, however, they can lead to excessive variance. Rejecting all samples classified as outliers, as suggested in previous work, leads to estimates that are too low and can cause undesirable artifacts. In this paper, we show how samples can be reweighted depending on their contribution and sampling frequency such that the finite-sample estimate gets closer to the correct expected value and the variance can be controlled. For this, we first derive a theory for how samples should ideally be reweighted and that this would require the probability density function of the optimal sampling strategy. As this PDF is generally unknown, we show how the discrepancy between the optimal and the actual sampling strategy can be estimated and used for reweighting in practice. We describe an efficient algorithm that allows for the necessary analysis of per-pixel sample distributions in the context of Monte Carlo Rendering without storing any individual samples, with only minimal changes to the rendering algorithm. It causes negligible runtime overhead, works in constant memory, and is well-suited for parallel and progressive rendering. The reweighting runs as a fast postprocess, can be controlled interactively, and our approach is non-destructive in that the unbiased result can be reconstructed at any time. -

Path Tracing Estimators for Refractive Radiative Transfer
Path Tracing Estimators for Refractive Radiative Transfer ADITHYA PEDIREDLA, YASIN KARIMI CHALMIANI, MATTEO GIUSEPPE SCOPELLITI, MAYSAM CHAMAN- ZAR, SRINIVASA NARASIMHAN, and IOANNIS GKIOULEKAS, Carnegie Mellon University, USA Real capture Bidirectional path tracing (ours) Photon mapping Horizontal cross-section at center Real data BDPT (ours) PM Normalized Intensity Horizontal distance (in mm) Fig. 1. Simulating refractive radiative transfer using bidrectional path tracing. Our technique enables path tracing estimators such as particle tracing, next-event estimation, bidirectional path tracing (BDPT) for heterogeneous refractive media. Unlike photon mapping (PM), path tracing estimators are unbiased and do not introduce artifacts besides noise. The above teaser shows that the proposed path tracing technique matches the real data acquired from an acousto-optic setup (ultrasound frequency: 813 kHz, 3 mean free paths, anisotropy 6 = 0.85) more accurately compared to photon mapping. Notice the complex caustics formed in a scattering medium whose refractive index field is altered using ultrasound. For more details and the reasons behind capture system imperfections, see Section 7.2. Our renderer can accelerate developments in acousto-optics, photo-acoustics, and schlieren imaging applications. The rendering time for BDPT and PM is 2.6 hrs on a cluster of 100 72-core (AWS c5n.18xlarge) machines. Rendering radiative transfer through media with a heterogeneous refractive imaging, and acousto-optic imaging, and can facilitate the development of index is challenging because the continuous refractive index variations re- inverse rendering techniques for related applications. sult in light traveling along curved paths. Existing algorithms are based on photon mapping techniques, and thus are biased and result in strong arti- CCS Concepts: • Computing methodologies → Computational pho- facts. -

Multiresolution Radiosity Caching for Efficient Preview and Final Quality
Multiresolution Radiosity Caching for Efficient Preview and Final Quality Global Illumination in Movies Per H. Christensen George Harker Jonathan Shade Brenden Schubert Dana Batali Pixar Technical Memo #12-06 — July, 2012 Pixar Animation Studios Figure 1: Two scenes from the CG movie ‘Monsters University’. Top row: direct illumination. Bottom row: global illumination — images such as these render more than 30 times faster with radiosity caching. c Disney/Pixar. Abstract 1 Introduction We present a multiresolution radiosity caching method that allows Recently there has been a surge in the use of global illumination global illumination to be computed efficiently in a single pass in (“color bleeding”) in CG movies and special effects, motivated by complex CG movie production scenes. the faster lighting design and more realistic lighting that it enables. The most widely used methods are distribution ray tracing, path For distribution ray tracing in production scenes, the bottleneck is tracing, and point-based global illumination; for an overview of the time spent evaluating complex shaders at the ray hit points. We these please see the course notes by Krivˇ anek´ et al. [2010]. speed up this shader evaluation time for global illumination by sep- arating out the view-independent component and caching its result The ray-traced global illumination methods (distribution ray tracing — the radiosity. Our cache contains three resolutions of the radios- and path tracing) are slow if the scenes have not only very complex ity; the resolution used for a given ray is selected using the ray’s base geometry but also very complex and programmable displace- differential. -

Efficient Sampling of Products of Functions Using Wavelets M.S. Thesis
Efficient sampling of products of functions using wavelets M.S. Thesis Petrik Clarberg Department of Computer Science Lund University Advisor: Tomas Akenine-M¨oller Department of Computer Science Lund University March 2005 Abstract This thesis presents a novel method for importance sampling the product of two- dimensional functions. The functions are represented as wavelets, which enables rapid computation of the product as well as efficient compression. The sampling is done by computing wavelet coefficients for the product on-the-fly, and hierarchically sampling the wavelet tree. The wavelet multiplication is guided by the sampling distribution. Hence, the proposed method is very efficient as it avoids a full computation of the prod- uct. The generated sampling distribution is superior to previous methods, as it exactly matches the probability density of the product of the two functions. As an application, the method is applied to the problem of rendering a virtual scene with realistic mea- sured materials under complex direct illumination provided by a high-dynamic range environment map. i ii Contents 1 Introduction 1 1.1 Previous Work . 2 1.2 Outline . 3 2 Wavelets 5 2.1 The Haar Basis . 5 2.2 The 2D Haar Basis . 6 2.3 Lossy Compression . 7 2.4 2D Wavelet Product . 7 2.5 Optimized Product . 9 2.6 Implementation . 9 3 Sampling 11 3.1 Monte Carlo Integration . 11 3.2 Importance Sampling . 12 3.3 Distribution of Samples . 12 3.4 Wavelet Importance Sampling . 13 3.4.1 Preliminaries . 13 3.4.2 Random Sampling – Single Sample . 14 3.4.3 Random Sampling – Multiple Samples . -

Physically Based 3D Rendering Using Unbiased Ray Tracing Render Engine
Vadim Morozov PHYSICALLY BASED 3D RENDERING USING UNBIASED RAY TRACING RENDER ENGINE Bachelor’s thesis Information Technology 2019 Author (authors) Degree Time Vadim Morozov Bachelor of October 2019 Engineering Thesis title 50 Pages Physically based 3D rendering using 4 Pages of aPPendices unbiased ray tracing render engine Commissioned by Supervisor Matti Juutilainen Abstract The thesis covered the toPic of 3D rendering. The main focus was on the Physically based rendering workflow that allows creating Photorealistic 3D graPhics. The objective of the thesis was to Prove that the technology evolved and develoPed so that almost any user with a Personal computer and essential knowledge is caPable for creating Photorealistic and Physically accurate images. The main research methods were an online research on different resources and Professional literature. The study covered main concePts and terms of lighting and materials in Physically based 3D rendering. Also, the main PrinciPles and technologies of rendering and the market of render engines was reviewed and analyzed. The goal of the Practical Part was to test the theory introduced and create the computer generated imagery in order to Prove the main ProPosition of the study. It included working in a dedicated software for 3D modeling and using AMD Radeon™ ProRender as main rendering software. The implementation Part consisted of detailed descriPtion of every steP of the Project creation. The whole Process from modeling to the final image outPut was explained. The final results of the study were 8 computer generated images that indicate the implementation was successful, the goal of the study was reached and it is Proved the initial ProPosition. -

Kerkythea 2008: Rendering, Iluminação E Materiais Recolha De Informação Sobre Rendering Em Kerkythea
Kerkythea 2008: Rendering, Iluminação e Materiais Recolha de informação sobre Rendering em Kerkythea. Fautl. 52013 Victor Ferreira Lista geral de Tutoriais: http://www.kerkythea.net/forum/viewtopic.php?f=16&t=5720 Luzes Tipos de luzes do Kerkythea: Omni, spot, IES e Projection (projeção). Omni: é uma luz multidireccional, que emite raios do centro para todos os lados, como o sol ou a luz de uma simples lâmpada incadescente. Spot: é uma luz direcional, como um foco, com um ângulo mais largo ou mais estreito de iluminação. IES: é um tipo de luz que tem propriedades físicas de intensidade e distribuição da luz descritas em um arquivo com extensão .ies. O resultado é mais realista do que as Omni ou Spotlight simples. O KT fornece um arquivo como um exemplo, mas você pode encontrar muitos ficheiros IES na web. Muitos fabricantes partilham os arquivos 3D das suas luminárias juntamente com o ficheiro IES respectivo. Também se pode encontrar programas gratuitos que permitem uma visualização rápida da forma da luz IES sem precisar de a inserir no Kerkythea Controlo de edição visual: a posição e o raio de luz podem ser geridos também com o controlador que você pode encontrar no canto superior direito da janela. O controle deslizante assume funções diferentes dependendo do tipo de luz que for seleccionado: o raio para a omni. HotSpot/falloff para a spot e largura/altura para projetor. Atenção: Quando se selecciona uma luz (Omni ou IES) aparece uma esfera amarela,que representa a dimensão do emissor. Isto depende do valor do raio, expresso em metros. -

Probabilistic Connections for Bidirectional Path Tracing
Eurographics Symposium on Rendering 2015 Volume 34 (2015), Number 4 J. Lehtinen and D. Nowrouzezahrai (Guest Editors) Probabilistic Connections for Bidirectional Path Tracing Stefan Popov 1 Ravi Ramamoorthi 2 Fredo Durand 3 George Drettakis 1 1 Inria 2 UC San Diego 3 MIT CSAIL Bidirectional Path Tracing Probabilistic Connections for Bidirectional Path Tracing Figure 1: Our Probabilistic Connections for Bidirectional Path Tracing approach importance samples connections to an eye sub-path, and greatly reduces variance, by considering and reusing multiple light sub-paths at once. Our approach (right) achieves much higher quality than bidirectional path-tracing on the left for the same computation time (~8.4 min). Abstract Bidirectional path tracing (BDPT) with Multiple Importance Sampling is one of the most versatile unbiased ren- dering algorithms today. BDPT repeatedly generates sub-paths from the eye and the lights, which are connected for each pixel and then discarded. Unfortunately, many such bidirectional connections turn out to have low con- tribution to the solution. Our key observation is that we can importance sample connections to an eye sub-path by considering multiple light sub-paths at once and creating connections probabilistically. We do this by storing light paths, and estimating probability mass functions of the discrete set of possible connections to all light paths. This has two key advantages: we efficiently create connections with low variance by Monte Carlo sampling, and we reuse light paths across different eye paths. We also introduce a caching scheme by deriving an approxima- tion to sub-path contribution which avoids high-dimensional path distance computations. Our approach builds on caching methods developed in the different context of VPLs.