A Physically Plausible Model for Rendering Highly Scattering Fluorescent Participating Media
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Path Tracing
Path Tracing Steve Rotenberg CSE168: Rendering Algorithms UCSD, Spring 2017 Irradiance Circumference of a Circle • The circumference of a circle of radius r is 2πr • In fact, a radian is defined as the angle you get on an arc of length r • We can represent the circumference of a circle as an integral 2휋 푐푖푟푐 = 푟푑휑 0 • This is essentially computing the length of the circumference as an infinite sum of infinitesimal segments of length 푟푑휑, over the range from 휑=0 to 2π Area of a Hemisphere • We can compute the area of a hemisphere by integrating ‘rings’ ranging over a second angle 휃, which ranges from 0 (at the north pole) to π/2 (at the equator) • The area of a ring is the circumference of the ring times the width 푟푑휃 • The circumference is going to be scaled by sin휃 as the rings are smaller towards the top of the hemisphere 휋 2 2휋 2 2 푎푟푒푎 = sin 휃 푟 푑휑 푑휃 = 2휋푟 0 0 Hemisphere Integral 휋 2 2휋 2 푎푟푒푎 = sin 휃 푟 푑휑 푑휃 0 0 • We are effectively computing an infinite summation of tiny rectangular area elements over a two dimensional domain. Each element has dimensions: sin 휃 푟푑휑 × 푟푑휃 Irradiance • Now, let’s assume that we are interested in computing the total amount of light arriving at some point on a surface • We are essentially integrating over all possible directions in the hemisphere above the surface (assuming it’s opaque and we’re not receiving translucent light from below the surface) • We are integrating the light intensity (or radiance) coming in from every direction • The total incoming radiance over all directions in the hemisphere -

Adjoints and Importance in Rendering: an Overview
IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS, VOL. 9, NO. 3, JULY-SEPTEMBER 2003 1 Adjoints and Importance in Rendering: An Overview Per H. Christensen Abstract—This survey gives an overview of the use of importance, an adjoint of light, in speeding up rendering. The importance of a light distribution indicates its contribution to the region of most interest—typically the directly visible parts of a scene. Importance can therefore be used to concentrate global illumination and ray tracing calculations where they matter most for image accuracy, while reducing computations in areas of the scene that do not significantly influence the image. In this paper, we attempt to clarify the various uses of adjoints and importance in rendering by unifying them into a single framework. While doing so, we also generalize some theoretical results—known from discrete representations—to a continuous domain. Index Terms—Rendering, adjoints, importance, light, ray tracing, global illumination, participating media, literature survey. æ 1INTRODUCTION HE use of importance functions started in neutron importance since it indicates how much the different parts Ttransport simulations soon after World War II. Im- of the domain contribute to the solution at the most portance was used (in different disguises) from 1983 to important part. Importance is also known as visual accelerate ray tracing [2], [16], [27], [78], [79]. Smits et al. [67] importance, view importance, potential, visual potential, value, formally introduced the use of importance for global -

Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017
ENGINEERING SOFTWARE DEVELOPMENT MADE EASY Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017 www.amcbridge.com Cloud Renderer for Autodesk Revit User Guide Contents Contents .................................................................................................................................................... 2 Welcome to Cloud Renderer for Autodesk Revit ...................................................................................... 3 Requirements and Installation .................................................................................................................. 5 Functionality.............................................................................................................................................. 8 Cloud Renderer Plug-in ......................................................................................................................... 8 Basic Settings ..................................................................................................................................... 8 Advanced Settings ........................................................................................................................... 10 Session manager ............................................................................................................................. 15 Single session view .......................................................................................................................... 17 Cloud Renderer on Microsoft® Azure® platfrom ............................................................................... -
3D Rendering Software Free Download Full Version Download 3 D Rendering - Best Software & Apps
3d rendering software free download full version Download 3 D Rendering - Best Software & Apps. NVIDIA Control Panel is a Windows utility tool, which lets users access critical functions of the NVIDIA drivers. With a comprehensive set of dropdown menus. OpenGL. An open-source graphics library. OpenGL is an open-source graphics standard for generating vector graphics in 2D as well as 3D. The cross-language Windows application has numerous functions. Autodesk Maya. Powerful 3D modeling, animation and rendering solution. Autodesk Maya is a highly professional solution for 3D modeling, animation and rendering in one complete and very powerful package.It has won several awards. Bring Your Models To Life With Powerful Rendering Tools. V-Ray is 3D model rendering software, usable with many different modelling programs but particularly compatible with SketchUp, Maya, Blender and others for. Envisioneer Express. Free 3D home design tool. Envisioneer Express is a multimedia application from Cadsoft. It is a free graphic design program that allows users to create plans for any residential. Virtual Lab. Discover the micro world with this virtual microscope. I was always fascinated by the science laboratory hours at school, when we had to use microscopes to literally discover new words, and test chemical. An extremely powerful 3D animation tool. modo has long been the application of choice for animation studios like Pixar Studios and Industrial Light and Magic. The latest update to modo improves upon. Voyager - Buy Bitcoin Crypto. A free program for Android, by Voyager Digital LLC. Voyager is a free software for Android, that belongs to the category 'Finance'. -

Indigo Manual
Contents Overview.............................................................................................4 About Indigo Renderer...........................................................................5 Licensing Indigo...................................................................................9 Indigo Licence activation......................................................................11 System Requirements..........................................................................14 About Installation................................................................................16 Installation on Windows.......................................................................17 Installation on Macintosh......................................................................19 Installation on Linux............................................................................20 Installing exporters for your modelling package........................................21 Working with the Indigo Interface Getting to know Indigo........................................................................23 Resolution.........................................................................................28 Tone Mapping.....................................................................................29 White balance....................................................................................36 Light Layers.......................................................................................37 Aperture Diffraction.............................................................................39 -

LIGHT TRANSPORT SIMULATION in REFLECTIVE DISPLAYS By
LIGHT TRANSPORT SIMULATION IN REFLECTIVE DISPLAYS by Zhanpeng Feng, B.S.E.E., M.S.E.E. A Dissertation In ELECTRICAL ENGINEERING DOCTOR OF PHILOSOPHY Dr. Brian Nutter Chair of the Committee Dr. Sunanda Mitra Dr. Tanja Karp Dr. Richard Gale Dr. Peter Westfall Peggy Gordon Miller Dean of the Graduate School May, 2012 Copyright 2012, Zhanpeng Feng Texas Tech University, Zhanpeng Feng, May 2012 ACKNOWLEDGEMENTS The pursuit of my Ph.D. has been a rather long journey. The journey started when I came to Texas Tech ten years ago, then took a change in direction when I went to California to work for Qualcomm in 2006. Over the course, I am privileged to have met the most amazing professionals in Texas Tech and Qualcomm. Without them I would have never been able to finish this dissertation. I begin by thanking my advisor, Dr. Brian Nutter, for introducing me to the brilliant world of research, and teaching me hands on skills to actually get something done. Dr. Nutter sets an example of excellence that inspired me to work as an engineer and researcher for my career. I would also extend my thanks to Dr. Mitra for her breadth and depth of knowledge; to Dr. Karp for her scientific rigor; to Dr. Gale for his expertise in color science and sense of humor; and to Dr. Westfall, for his great mind in statistics. They have provided me invaluable advice throughout the research. My colleagues and supervisors in Qualcomm also gave tremendous support and guidance along the path. Tom Fiske helped me establish my knowledge in optics from ground up and taught me how to use all the tools for optical measurements. -

The Photon Mapping Method
7 The Photon Mapping Method “I get by with a little help from my friends.” —John Lennon, 1940–1980 HOTON mapping is a practical approach for computing global illumination within complex P environments. Much like irradiance caching methods, photon mapping caches and reuses illumination information in the scene for efficiency. Photon mapping has also been successfully applied for computing lighting within, and in the presence of, participating media. In this chapter we briefly introduce the photon mapping technique. This sets the foundation for our contributions in the next chapter, which make volumetric photon mapping practical. 7.1 Algorithm Overview Photon mapping, introduced by Jensen[1995; 1996; 1997; 1998; 2001], is a practical approach for computing global illumination. At a high level, the algorithm consists of two main steps: Algorithm 7.1:PHOTONMAPPING() 1 PHOTONTRACING(); 2 RENDERUSINGPHOTONMAP(); In the first step, a lighting simulation is performed by tracing packets of energy, or photons, from light sources and storing these photons as they scatter within the scene. This processes 119 120 Algorithm 7.2:PHOTONTRACING() 1 n 0; e Æ 2 repeat 3 (l, pdf (l)) = CHOOSELIGHT(); 4 (xp , ~!p , ©p ) = GENERATEPHOTON(l ); ©p 5 TRACEPHOTON(xp , ~!p , pdf (l) ); 6 n 1; e ÅÆ 7 until photon map full ; 1 8 Scale power of all photons by ; ne results in a set of photon maps, which can be used to efficiently query lighting information. In the second pass, the final image is rendered using Monte Carlo ray tracing. This rendering step is made more efficient by exploiting the lighting information cached in the photon map. -

Lighting - the Radiance Equation
CHAPTER 3 Lighting - the Radiance Equation Lighting The Fundamental Problem for Computer Graphics So far we have a scene composed of geometric objects. In computing terms this would be a data structure representing a collection of objects. Each object, for example, might be itself a collection of polygons. Each polygon is sequence of points on a plane. The ‘real world’, however, is ‘one that generates energy’. Our scene so far is truly a phantom one, since it simply is a description of a set of forms with no substance. Energy must be generated: the scene must be lit; albeit, lit with virtual light. Computer graphics is concerned with the construction of virtual models of scenes. This is a relatively straightforward problem to solve. In comparison, the problem of lighting scenes is the major and central conceptual and practical problem of com- puter graphics. The problem is one of simulating lighting in scenes, in such a way that the computation does not take forever. Also the resulting 2D projected images should look as if they are real. In fact, let’s make the problem even more interesting and challenging: we do not just want the computation to be fast, we want it in real time. Image frames, in other words, virtual photographs taken within the scene must be produced fast enough to keep up with the changing gaze (head and eye moves) of Lighting - the Radiance Equation 35 Great Events of the Twentieth Century35 Lighting - the Radiance Equation people looking and moving around the scene - so that they experience the same vis- ual sensations as if they were moving through a corresponding real scene. -

CS 184: Problems and Questions on Rendering
CS 184: Problems and Questions on Rendering Ravi Ramamoorthi Problems 1. Define the terms Radiance and Irradiance, and give the units for each. Write down the formula (inte- gral) for irradiance at a point in terms of the illumination L(ω) incident from all directions ω. Write down the local reflectance equation, i.e. express the net reflected radiance in a given direction as an integral over the incident illumination. 2. Make appropriate approximations to derive the radiosity equation from the full rendering equation. 3. Match the surface material to the formula (and goniometric diagram shown in class). Also, give an example of a real material that reasonably closely approximates the mathematical description. Not all materials need have a corresponding diagram. The materials are ideal mirror, dark glossy, ideal diffuse, retroreflective. The formulae for the BRDF fr are 4 ka(R~ · V~ ), kb(R~ · V~ ) , kc/(N~ · V~ ), kdδ(R~), ke. 4. Consider the Cornell Box (as in the radiosity lecture, assume for now that this is essentially a room with only the walls, ceiling and floor. Assume for now, there are no small boxes or other furniture in the room, and that all surfaces are Lambertian. The box also has a small rectangular white light source at the center of the ceiling.) Assume we make careful measurements of the light source intensity and dimensions of the room, as well as the material properties of the walls, floor and ceiling. We then use these as inputs to our simple OpenGL renderer. Assuming we have been completely accurate, will the computer-generated picture be identical to a photograph of the same scene from the same location? If so, why? If not, what will be the differences? Ignore gamma correction and other nonlinear transfer issues. -

Probabilistic Connections for Bidirectional Path Tracing
Eurographics Symposium on Rendering 2015 Volume 34 (2015), Number 4 J. Lehtinen and D. Nowrouzezahrai (Guest Editors) Probabilistic Connections for Bidirectional Path Tracing Stefan Popov 1 Ravi Ramamoorthi 2 Fredo Durand 3 George Drettakis 1 1 Inria 2 UC San Diego 3 MIT CSAIL Bidirectional Path Tracing Probabilistic Connections for Bidirectional Path Tracing Figure 1: Our Probabilistic Connections for Bidirectional Path Tracing approach importance samples connections to an eye sub-path, and greatly reduces variance, by considering and reusing multiple light sub-paths at once. Our approach (right) achieves much higher quality than bidirectional path-tracing on the left for the same computation time (~8.4 min). Abstract Bidirectional path tracing (BDPT) with Multiple Importance Sampling is one of the most versatile unbiased ren- dering algorithms today. BDPT repeatedly generates sub-paths from the eye and the lights, which are connected for each pixel and then discarded. Unfortunately, many such bidirectional connections turn out to have low con- tribution to the solution. Our key observation is that we can importance sample connections to an eye sub-path by considering multiple light sub-paths at once and creating connections probabilistically. We do this by storing light paths, and estimating probability mass functions of the discrete set of possible connections to all light paths. This has two key advantages: we efficiently create connections with low variance by Monte Carlo sampling, and we reuse light paths across different eye paths. We also introduce a caching scheme by deriving an approxima- tion to sub-path contribution which avoids high-dimensional path distance computations. Our approach builds on caching methods developed in the different context of VPLs. -
A Progressive Error Estimation Framework for Photon Density Estimation
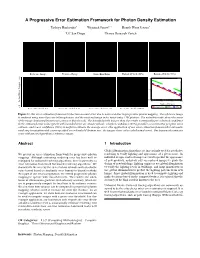
A Progressive Error Estimation Framework for Photon Density Estimation Toshiya Hachisuka∗ Wojciech Jaroszy;∗ Henrik Wann Jensen∗ ∗UC San Diego yDisney Research Zurich¨ Reference Image Rendered Image Noise/Bias Ratio Bounded Pixels (50%) Bounded Pixels (90%) 5 . 0 1.0 s e g a m I 0.1 r o r r E l a u t c 0.01 10 100 1000 8000 A Number of Iterations 0 . 0 actual error 90% 50% Error Threshold: 0.5 Error Threshold: 0.25 Error Threshold: 0.125 Error Threshold: 0.0625 Figure 1: Our error estimation framework takes into account error due to noise and bias in progressive photon mapping. The reference image is rendered using more than one billion photons, and the rendered image is the result using 15M photons. The noise/bias ratio shows the areas of the image dominated by noise (in green) or bias (in red). The bounded pixels images show the results corresponding to a desired confidence in the estimated error value (pixels with bounded error are shown yellow): a higher confidence (90%) provides a conservative per pixel error estimate, and lower confidence (50%) is useful to estimate the average error. One application of our error estimation framework is automatic rendering termination with a user-specified error threshold (bottom row: the images show color-coded actual error). Our framework estimates error without any input from a reference image. Abstract 1 Introduction Global illumination algorithms are increasingly used for predictive We present an error estimation framework for progressive photon rendering to verify lighting and appearance of a given scene. -

Light (Technical)
Chapter 21 Light (technical) In this chapter we will describe in more detail how light and reflections are properly measured and represented. These concepts may not be necessary for doing casual com- puter graphics, but they can become important in order to do high quality rendering. Such high quality rendering is often done using stand alone software and does not use the same rendering pipeline as OpenGL. We will cover some of this material, as it is perhaps the most developed part of advanced computer graphics. This chapter will be covering material at a more advanced level than the rest of this book. For an even more detailed treatment of this material, see Jim Arvo’s PhD thesis [3] and Eric Veach’s PhD thesis [71]. There are two steps needed to understand high quality light simulation. First of all, one needs to understand the proper units needed to measure light and reflection. This understanding directly leads to equations which model how light behaves in a scene. Secondly, one needs algorithms that compute approximate solutions to these equations. These algorithms make heavy use of the ray tracing infrastructure described in Chapter 20. In this chapter we will focuson the more fundamental aspect of deriving the appropriate equations, and only touch on the subsequent algorithmic issues. For more on such issues, the interested reader should see [71, 30]. Our basic mental model of light is that of “geometric optics”. We think of light as a field of photons flying through space. In free space, each photon flies unmolested in a straight line, and each moves at the same speed.