DOCSLIB.ORG

Pathtracinginproduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pathtracinginproduction Path tracing in Production Part 1: Modern Path Tracing Luca F������� (Organizer) Johannes H����� (Organizer) Weta Digital Weta Digital Daniel H��������� Christopher K���� Marc D����� Jorge S����������� Animal Logic Sony Imageworks Weta Digital Weta Digital SIGGRAPH 2019 Course Notes Imagery from recent movie productions, featuring difficult light transport, massive geometric complexity, intricate material detail, as well as volumetric effects. The LEGO Movie 2: The Second Part Image courtesy of Animal Logic, ©2019 Warner Bros. Entertainment Inc. ©The LEGO Group. All rights reserved. Spiderman: Homecoming ©2017 CTMG, Inc. All rights reserved. Alita: Battle Angel ©2018 Twentieth Century Fox Film Corporation. All rights reserved. Permission to make digital or hard copies of part or all of this work for personal or class- room use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for third-party components of this work must be honored. For all other uses, con- tact the Owner/Author. Copyright is held by the owner/author(s). SIGGRAPH ’19 Courses, July 28 - August 01, 2019, Los Angeles, CA, USA ACM 978-1-4503-6307-5/19/07. 10.1145/3305366.3328079 P��� ������� �� P��������� Abstract In the past few years the movie industry has switched over from stochastic rasterisation approaches to using phys- ically based light transport simulation: path tracing in production has become ubiquitous across studios. The new approach came with undisputed advantages such as consistent lighting,progressive previews,and fresh code bases. But also abandoning 30 years of experience meant some hard cuts affecting all stages such as lighting, look devel- opment, geometric modelling, scene description formats, the way we schedule for multi-threading, just to name a few. This means there is a rich set of people involved and as an expert in either one of these aspects it is easy to lose track of the big picture. This is part I of a full-day course,and it focuses on the necessary background knowledge. In this part,we would like to provide context for everybody interested in understanding the challenges behind writing renderers intended for movie production work. In particular we will give an insight into movie production requirements for new students and academic researchers. On the other side we will lay a solid mathematical foundation to develop new ideas to solve problems in this context. To further illustrate, part II of the course will focus on materials (acquisition and production requirements) and showcase practical efforts by prominent professionals in the field,pointing out unexpected challenges encountered in new shows and unsolved problems as well as room for future work wherever appropriate. SIGGRAPH 2019 Course Notes: Path tracing in Production — Part 1 Page 2 / 105 P��� ������� �� P��������� Contents 1 Introduction to path tracing and Monte Carlo sampling 4 1.1 Transport equations ........................................ 4 1.1.1 Assumptions ....................................... 4 1.1.2 Counting photons ..................................... 4 1.1.3 Events that change photon count ............................. 6 1.1.4 The radiative transfer equation .............................. 8 1.2 The path space ........................................... 9 1.3 The Monte Carlo method ...................................... 11 1.4 Colour formation in a renderer ................................... 12 1.4.1 Colour reproduction ................................... 12 1.4.2 Where to get input spectra from .............................. 13 1.4.3 Colour noise ........................................ 14 1.4.4 Importance sampling ................................... 14 1.4.5 Radiometry vs. Photometry ................................ 15 1.5 Path construction techniques .................................... 16 1.5.1 Path tracing ........................................ 16 1.5.2 Next event estimation ................................... 16 1.5.3 Light tracing ........................................ 16 1.5.4 Photon mapping-based approaches ............................ 17 1.5.5 Markov chain-based methods ............................... 17 1.6 Conclusion ............................................. 18 2 Monte Carlo integration 22 2.1 Introduction: a holistic look at integration theory ......................... 22 2.2 Problem statement ......................................... 23 2.2.1 The Riemann integral ................................... 23 2.2.2 Integrable functions .................................... 24 2.2.3 Interlude: the Fundamental Theorem of Calculus ..................... 26 2.2.4 The Lebesgue integral ................................... 26 2.2.5 A topological interlude .................................. 28 2.2.6 Integrals in higher dimensions .............................. 30 2.3 Numerical integration ....................................... 31 2.3.1 Lagrange interpolation .................................. 32 2.3.2 Improving convergence for numerical quadrature .................... 34 2.3.3 Integrals in higher dimensions .............................. 35 2.4 Monte Carlo integration ...................................... 36 2.4.1 Estimation error in Monte Carlo integration ....................... 36 2.4.2 Interlude: random number generation .......................... 37 2.4.3 Variance reduction techniques .............................. 37 2.4.4 Quasi-Random sequences and Monte Carlo ....................... 39 2.4.5 A quality metric on sequences ............................... 40 2.4.6 Error bounds ....................................... 41 2.5 Markov chain Monte Carlo ..................................... 42 2.5.1 Discussion ......................................... 43 Appendices 43 2.A Riemann on Riemann’s integral ................................... 43 SIGGRAPH 2019 Course Notes: Path tracing in Production — Part 1 Page 1 / 105 P��� ������� �� P��������� 3 A modular path sampling framework 47 3.1 Path integral formulation including participating media ...................... 47 3.2 Computing the integral ....................................... 49 3.2.1 The Monte Carlo approach ................................ 49 3.2.2 Multiple Importance Sampling .............................. 50 3.2.3 Practical MIS ....................................... 50 3.3 Path sampling technique zoo .................................... 52 3.3.1 Path extensions ...................................... 52 3.3.2 Splitting .......................................... 53 3.3.3 Shift mappings ....................................... 54 3.3.4 Markov-Chain methods et al. ............................... 54 3.3.5 Multi spectral sampling .................................. 55 3.3.6 Local techniques - path guiding .............................. 55 3.3.7 Discussion ......................................... 55 3.4 Modular light transport via the vertex graph ............................ 56 3.4.1 Path extensions ...................................... 56 3.4.2 Shift techniques ...................................... 57 3.4.3 Volumes and Transparency ................................ 58 3.4.4 Photon mapping / VCM .................................. 58 3.4.5 Memory management ................................... 60 3.4.6 Discussion ......................................... 60 4 Finding good paths 64 4.1 Path reconnection techniques for stereoscopic rendering and distribution effects ......... 64 4.1.1 Multi-view rendering ................................... 65 4.1.2 Primary path reconnection ................................ 65 4.1.3 Higher dimensions .................................... 66 4.1.4 Motion Blur ........................................ 67 4.1.5 Computing path throughput ............................... 67 4.1.6 Adapting to projected velocity ............................... 68 4.1.7 Depth of Field ....................................... 69 4.1.8 Simultaneous effects .................................... 70 4.1.9 Summary ......................................... 70 4.2 Efficient next-event estimation in Manuka ............................. 70 4.2.1 A history of NEE in Manuka ............................... 71 4.2.2 Building a light hierarchy ................................. 72 4.2.3 Sampling the light hierarchy ................................ 74 4.2.4 Occlusion and radiance biasing .............................. 76 4.2.5 Product sampling ..................................... 78 4.2.6 Summary ......................................... 79 5 Volumes 81 5.1 Intersecting Rays with Volumes .................................. 81 5.1.1 Dealing with Overlap ................................... 82 5.1.2 Aggregate Volumes .................................... 83 5.1.3 Boundary Driven Volumes ................................ 83 5.2 Light Transport in Volumes .................................... 84 5.2.1 Sampling homogeneous transmittance .......................... 85 5.2.2 Sampling heterogeneous transmittance .......................... 87 5.2.3 Next Event Estimation in Volumes ............................ 90 5.2.4 Beyond single scattering .................................. 92 5.2.5 Emissive Volumes ..................................... 94 SIGGRAPH 2019 Course Notes: Path tracing in Production — Part 1 Page 2 / 105 P��� ������� �� P��������� 5.3 Production Features ........................................ 95 5.3.1 Large Datasets ....................................... 95 5.3.2
Load more

Recommended publications
  • Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017
    ENGINEERING SOFTWARE DEVELOPMENT MADE EASY Cloud Renderer for Autodesk® Revit® User Guide June 21, 2017 www.amcbridge.com Cloud Renderer for Autodesk Revit User Guide Contents Contents .................................................................................................................................................... 2 Welcome to Cloud Renderer for Autodesk Revit ...................................................................................... 3 Requirements and Installation .................................................................................................................. 5 Functionality.............................................................................................................................................. 8 Cloud Renderer Plug-in ......................................................................................................................... 8 Basic Settings ..................................................................................................................................... 8 Advanced Settings ........................................................................................................................... 10 Session manager ............................................................................................................................. 15 Single session view .......................................................................................................................... 17 Cloud Renderer on Microsoft® Azure® platfrom ...............................................................................
    [Show full text]
  • 3D Rendering Software Free Download Full Version Download 3 D Rendering - Best Software & Apps
    3d rendering software free download full version Download 3 D Rendering - Best Software & Apps. NVIDIA Control Panel is a Windows utility tool, which lets users access critical functions of the NVIDIA drivers. With a comprehensive set of dropdown menus. OpenGL. An open-source graphics library. OpenGL is an open-source graphics standard for generating vector graphics in 2D as well as 3D. The cross-language Windows application has numerous functions. Autodesk Maya. Powerful 3D modeling, animation and rendering solution. Autodesk Maya is a highly professional solution for 3D modeling, animation and rendering in one complete and very powerful package.It has won several awards. Bring Your Models To Life With Powerful Rendering Tools. V-Ray is 3D model rendering software, usable with many different modelling programs but particularly compatible with SketchUp, Maya, Blender and others for. Envisioneer Express. Free 3D home design tool. Envisioneer Express is a multimedia application from Cadsoft. It is a free graphic design program that allows users to create plans for any residential. Virtual Lab. Discover the micro world with this virtual microscope. I was always fascinated by the science laboratory hours at school, when we had to use microscopes to literally discover new words, and test chemical. An extremely powerful 3D animation tool. modo has long been the application of choice for animation studios like Pixar Studios and Industrial Light and Magic. The latest update to modo improves upon. Voyager - Buy Bitcoin Crypto. A free program for Android, by Voyager Digital LLC. Voyager is a free software for Android, that belongs to the category 'Finance'.
    [Show full text]
  • Indigo Manual
    Contents Overview.............................................................................................4 About Indigo Renderer...........................................................................5 Licensing Indigo...................................................................................9 Indigo Licence activation......................................................................11 System Requirements..........................................................................14 About Installation................................................................................16 Installation on Windows.......................................................................17 Installation on Macintosh......................................................................19 Installation on Linux............................................................................20 Installing exporters for your modelling package........................................21 Working with the Indigo Interface Getting to know Indigo........................................................................23 Resolution.........................................................................................28 Tone Mapping.....................................................................................29 White balance....................................................................................36 Light Layers.......................................................................................37 Aperture Diffraction.............................................................................39
    [Show full text]
  • Physically Based Rendering of Synthetic Objects in Real Environments
    Linköping studies in science and technology. Dissertation, No. 1717 PHYSICALLY BASED RENDERING OF SYNTHETIC OBJECTS IN REAL ENVIRONMENTS Joel Kronander Division of Media and Information Technology Department of Science and Technology Linköping University, SE-601 74 Norrköping, Sweden Norrköping, December 2015 Description of the cover image Rendering of virtual furniture illuminated with spatially varying real world illumination captured in a physical environment at IKEA Communications AB. The virtual scene was modeled by Sören and Per Larsson. Physically based rendering of synthetic objects in real environments Copyright © 2015 Joel Kronander (unless otherwise noted) Division of Media and Information Technology Department of Science and Technology Campus Norrköping, Linköping University SE-601 74 Norrköping, Sweden ISBN: 978-91-7685-912-4 ISSN: 0345-7524 Printed in Sweden by LiU-Tryck, Linköping, 2015 Abstract This thesis presents methods for photorealistic rendering of virtual objects so that they can be seamlessly composited into images of the real world. To generate predictable and consistent results, we study physically based methods, which simulate how light propagates in a mathematical model of the augmented scene. This computationally challenging problem demands both efficient and accurate simulation of the light transport in the scene, as well as detailed modeling of the geometries, illumination conditions, and material properties. In this thesis, we discuss and formulate the challenges inherent in these steps and present several methods to make the process more efficient. In particular, the material contained in this thesis addresses four closely related areas: HDR imaging, IBL, reflectance modeling, and efficient rendering. The thesis presents a new, statistically motivated algorithm for HDR reconstruction from raw camera data combining demosaicing, denoising, and HDR fusion in a single processing operation.
    [Show full text]
  • Probabilistic Connections for Bidirectional Path Tracing
    Eurographics Symposium on Rendering 2015 Volume 34 (2015), Number 4 J. Lehtinen and D. Nowrouzezahrai (Guest Editors) Probabilistic Connections for Bidirectional Path Tracing Stefan Popov 1 Ravi Ramamoorthi 2 Fredo Durand 3 George Drettakis 1 1 Inria 2 UC San Diego 3 MIT CSAIL Bidirectional Path Tracing Probabilistic Connections for Bidirectional Path Tracing Figure 1: Our Probabilistic Connections for Bidirectional Path Tracing approach importance samples connections to an eye sub-path, and greatly reduces variance, by considering and reusing multiple light sub-paths at once. Our approach (right) achieves much higher quality than bidirectional path-tracing on the left for the same computation time (~8.4 min). Abstract Bidirectional path tracing (BDPT) with Multiple Importance Sampling is one of the most versatile unbiased ren- dering algorithms today. BDPT repeatedly generates sub-paths from the eye and the lights, which are connected for each pixel and then discarded. Unfortunately, many such bidirectional connections turn out to have low con- tribution to the solution. Our key observation is that we can importance sample connections to an eye sub-path by considering multiple light sub-paths at once and creating connections probabilistically. We do this by storing light paths, and estimating probability mass functions of the discrete set of possible connections to all light paths. This has two key advantages: we efficiently create connections with low variance by Monte Carlo sampling, and we reuse light paths across different eye paths. We also introduce a caching scheme by deriving an approxima- tion to sub-path contribution which avoids high-dimensional path distance computations. Our approach builds on caching methods developed in the different context of VPLs.
    [Show full text]
  • Production Rendering Ian Stephenson (Ed.) Production Rendering
    Production Rendering Ian Stephenson (Ed.) Production Rendering Design and Implementation 12 3 Ian Stephenson, DPhil National Centre for Computer Animation, Bournemouth, UK British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library Library of Congress Cataloging-in-Publication Data A catalog record for this book is available from the Library of Congress Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms of licences issued by the Copyright Licensing Agency. Enquiries concerning reproduction outside those terms should be sent to the publishers. ISBN 1-85233-821-0 Springer-Verlag London Berlin Heidelberg Springer ScienceϩBusiness Media springeronline.com © Springer London Limited 2005 Printed in the United States of America The use of registered names, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant laws and regulations and therefore free for general use. The publisher makes no representation, express or implied, with regard to the accuracy of the information contained in this book and cannot accept any legal responsibility or liability for any errors or omissions that may be made. Typeset by Gray Publishing, Tunbridge Wells, UK Printed and bound in the United States of America 34/3830-543210 Printed on acid-free paper SPIN 10951729 We dedicate this book to: Amanda Rochfort, Cheryl M.
    [Show full text]
  • A Progressive Error Estimation Framework for Photon Density Estimation
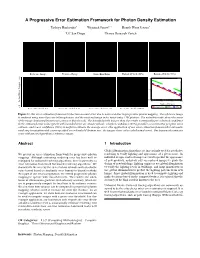
    A Progressive Error Estimation Framework for Photon Density Estimation Toshiya Hachisuka∗ Wojciech Jaroszy;∗ Henrik Wann Jensen∗ ∗UC San Diego yDisney Research Zurich¨ Reference Image Rendered Image Noise/Bias Ratio Bounded Pixels (50%) Bounded Pixels (90%) 5 . 0 1.0 s e g a m I 0.1 r o r r E l a u t c 0.01 10 100 1000 8000 A Number of Iterations 0 . 0 actual error 90% 50% Error Threshold: 0.5 Error Threshold: 0.25 Error Threshold: 0.125 Error Threshold: 0.0625 Figure 1: Our error estimation framework takes into account error due to noise and bias in progressive photon mapping. The reference image is rendered using more than one billion photons, and the rendered image is the result using 15M photons. The noise/bias ratio shows the areas of the image dominated by noise (in green) or bias (in red). The bounded pixels images show the results corresponding to a desired confidence in the estimated error value (pixels with bounded error are shown yellow): a higher confidence (90%) provides a conservative per pixel error estimate, and lower confidence (50%) is useful to estimate the average error. One application of our error estimation framework is automatic rendering termination with a user-specified error threshold (bottom row: the images show color-coded actual error). Our framework estimates error without any input from a reference image. Abstract 1 Introduction Global illumination algorithms are increasingly used for predictive We present an error estimation framework for progressive photon rendering to verify lighting and appearance of a given scene.
    [Show full text]
  • Reweighting Firefly Samples for Improved Finite-Sample Monte
    Volume xx (200y), Number z, pp. 1–10 Reweighting Firefly Samples for Improved Finite-Sample Monte Carlo Estimates Tobias Zirr, Johannes Hanika, and Carsten Dachsbacher Karlsruhe Institute of Technology Abstract Samples with high contribution but low probability density, often called fireflies, occur in all practical Monte Carlo estima- tors and are part of computing unbiased estimates. For finite-sample estimates, however, they can lead to excessive variance. Rejecting all samples classified as outliers, as suggested in previous work, leads to estimates that are too low and can cause undesirable artifacts. In this paper, we show how samples can be reweighted depending on their contribution and sampling frequency such that the finite-sample estimate gets closer to the correct expected value and the variance can be controlled. For this, we first derive a theory for how samples should ideally be reweighted and that this would require the probability density function of the optimal sampling strategy. As this PDF is generally unknown, we show how the discrepancy between the optimal and the actual sampling strategy can be estimated and used for reweighting in practice. We describe an efficient algorithm that allows for the necessary analysis of per-pixel sample distributions in the context of Monte Carlo Rendering without storing any individual samples, with only minimal changes to the rendering algorithm. It causes negligible runtime overhead, works in constant memory, and is well-suited for parallel and progressive rendering. The reweighting runs as a fast postprocess, can be controlled interactively, and our approach is non-destructive in that the unbiased result can be reconstructed at any time.
    [Show full text]
  • Path Tracing Estimators for Refractive Radiative Transfer
    Path Tracing Estimators for Refractive Radiative Transfer ADITHYA PEDIREDLA, YASIN KARIMI CHALMIANI, MATTEO GIUSEPPE SCOPELLITI, MAYSAM CHAMAN- ZAR, SRINIVASA NARASIMHAN, and IOANNIS GKIOULEKAS, Carnegie Mellon University, USA Real capture Bidirectional path tracing (ours) Photon mapping Horizontal cross-section at center Real data BDPT (ours) PM Normalized Intensity Horizontal distance (in mm) Fig. 1. Simulating refractive radiative transfer using bidrectional path tracing. Our technique enables path tracing estimators such as particle tracing, next-event estimation, bidirectional path tracing (BDPT) for heterogeneous refractive media. Unlike photon mapping (PM), path tracing estimators are unbiased and do not introduce artifacts besides noise. The above teaser shows that the proposed path tracing technique matches the real data acquired from an acousto-optic setup (ultrasound frequency: 813 kHz, 3 mean free paths, anisotropy 6 = 0.85) more accurately compared to photon mapping. Notice the complex caustics formed in a scattering medium whose refractive index field is altered using ultrasound. For more details and the reasons behind capture system imperfections, see Section 7.2. Our renderer can accelerate developments in acousto-optics, photo-acoustics, and schlieren imaging applications. The rendering time for BDPT and PM is 2.6 hrs on a cluster of 100 72-core (AWS c5n.18xlarge) machines. Rendering radiative transfer through media with a heterogeneous refractive imaging, and acousto-optic imaging, and can facilitate the development of index is challenging because the continuous refractive index variations re- inverse rendering techniques for related applications. sult in light traveling along curved paths. Existing algorithms are based on photon mapping techniques, and thus are biased and result in strong arti- CCS Concepts: • Computing methodologies → Computational pho- facts.
    [Show full text]
  • Pencil Light Transport
    Pencil Light Transport by Mauro Steigleder A thesis presented to the University of Waterloo in fulfilment of the thesis requirement for the degree of Doctor of Philosophy in Computer Science Waterloo, Ontario, Canada, 2005 c Mauro Steigleder 2005 AUTHOR’S DECLARATION FOR ELECTRONIC SUBMISSION OF A THESIS I hereby declare that I am the sole author of this thesis. This is a true copy of the thesis, including any required final revisions, as accepted by my examiners. I understand that my thesis may be made electronically available to the public. ii Abstract Global illumination is an important area of computer graphics, having direct applications in architectural visualization, lighting design and entertainment. Indirect illumination ef- fects such as soft shadows, color bleeding, caustics and glossy reflections provide essential visual information about the interaction of different regions of the environment. Global illumination is a research area that deals with these illumination effects. Interactivity is also a desirable feature for many computer graphics applications, especially with unre- stricted manipulation of the environment and lighting conditions. However, the design of methods that can handle both unrestricted interactivity and global illumination effects on environments of reasonable complexity is still an open challenge. We present a new formulation of the light transport equation, called pencil light trans- port, that makes progress towards this goal by exploiting graphics hardware rendering features. The proposed method performs the transport of radiance over a scene using sets of pencils. A pencil object consists of a center of projection and some associated di- rectional data. We show that performing the radiance transport using pencils is suitable for implementation on current graphics hardware.
    [Show full text]
  • Multiresolution Radiosity Caching for Efficient Preview and Final Quality
    Multiresolution Radiosity Caching for Efficient Preview and Final Quality Global Illumination in Movies Per H. Christensen George Harker Jonathan Shade Brenden Schubert Dana Batali Pixar Technical Memo #12-06 — July, 2012 Pixar Animation Studios Figure 1: Two scenes from the CG movie ‘Monsters University’. Top row: direct illumination. Bottom row: global illumination — images such as these render more than 30 times faster with radiosity caching. c Disney/Pixar. Abstract 1 Introduction We present a multiresolution radiosity caching method that allows Recently there has been a surge in the use of global illumination global illumination to be computed efficiently in a single pass in (“color bleeding”) in CG movies and special effects, motivated by complex CG movie production scenes. the faster lighting design and more realistic lighting that it enables. The most widely used methods are distribution ray tracing, path For distribution ray tracing in production scenes, the bottleneck is tracing, and point-based global illumination; for an overview of the time spent evaluating complex shaders at the ray hit points. We these please see the course notes by Krivˇ anek´ et al. [2010]. speed up this shader evaluation time for global illumination by sep- arating out the view-independent component and caching its result The ray-traced global illumination methods (distribution ray tracing — the radiosity. Our cache contains three resolutions of the radios- and path tracing) are slow if the scenes have not only very complex ity; the resolution used for a given ray is selected using the ray’s base geometry but also very complex and programmable displace- differential.
    [Show full text]
  • Efficient Sampling of Products of Functions Using Wavelets M.S. Thesis
    Efficient sampling of products of functions using wavelets M.S. Thesis Petrik Clarberg Department of Computer Science Lund University Advisor: Tomas Akenine-M¨oller Department of Computer Science Lund University March 2005 Abstract This thesis presents a novel method for importance sampling the product of two- dimensional functions. The functions are represented as wavelets, which enables rapid computation of the product as well as efficient compression. The sampling is done by computing wavelet coefficients for the product on-the-fly, and hierarchically sampling the wavelet tree. The wavelet multiplication is guided by the sampling distribution. Hence, the proposed method is very efficient as it avoids a full computation of the prod- uct. The generated sampling distribution is superior to previous methods, as it exactly matches the probability density of the product of the two functions. As an application, the method is applied to the problem of rendering a virtual scene with realistic mea- sured materials under complex direct illumination provided by a high-dynamic range environment map. i ii Contents 1 Introduction 1 1.1 Previous Work . 2 1.2 Outline . 3 2 Wavelets 5 2.1 The Haar Basis . 5 2.2 The 2D Haar Basis . 6 2.3 Lossy Compression . 7 2.4 2D Wavelet Product . 7 2.5 Optimized Product . 9 2.6 Implementation . 9 3 Sampling 11 3.1 Monte Carlo Integration . 11 3.2 Importance Sampling . 12 3.3 Distribution of Samples . 12 3.4 Wavelet Importance Sampling . 13 3.4.1 Preliminaries . 13 3.4.2 Random Sampling – Single Sample . 14 3.4.3 Random Sampling – Multiple Samples .
    [Show full text]