A Linear-Time Self-Interpreter of a Reversible Imperative Language
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Engineering Definitional Interpreters
Reprinted from the 15th International Symposium on Principles and Practice of Declarative Programming (PPDP 2013) Engineering Definitional Interpreters Jan Midtgaard Norman Ramsey Bradford Larsen Department of Computer Science Department of Computer Science Veracode Aarhus University Tufts University [email protected] [email protected] [email protected] Abstract In detail, we make the following contributions: A definitional interpreter should be clear and easy to write, but it • We investigate three styles of semantics, each of which leads to may run 4–10 times slower than a well-crafted bytecode interpreter. a family of definitional interpreters. A “family” is characterized In a case study focused on implementation choices, we explore by its representation of control contexts. Our best-performing ways of making definitional interpreters faster without expending interpreter, which arises from a natural semantics, represents much programming effort. We implement, in OCaml, interpreters control contexts using control contexts of the metalanguage. based on three semantics for a simple subset of Lua. We com- • We evaluate other implementation choices: how names are rep- pile the OCaml to 86 native code, and we systematically inves- x resented, how environments are represented, whether the inter- tigate hundreds of combinations of algorithms and data structures. preter has a separate “compilation” step, where intermediate re- In this experimental context, our fastest interpreters are based on sults are stored, and how loops are implemented. natural semantics; good algorithms and data structures make them 2–3 times faster than na¨ıve interpreters. Our best interpreter, cre- • We identify combinations of implementation choices that work ated using only modest effort, runs only 1.5 times slower than a well together. -

Open Programming Language Interpreters
Open Programming Language Interpreters Walter Cazzolaa and Albert Shaqiria a Università degli Studi di Milano, Italy Abstract Context: This paper presents the concept of open programming language interpreters, a model to support them and a prototype implementation in the Neverlang framework for modular development of programming languages. Inquiry: We address the problem of dynamic interpreter adaptation to tailor the interpreter’s behaviour on the task to be solved and to introduce new features to fulfil unforeseen requirements. Many languages provide a meta-object protocol (MOP) that to some degree supports reflection. However, MOPs are typically language-specific, their reflective functionality is often restricted, and the adaptation and application logic are often mixed which hardens the understanding and maintenance of the source code. Our system overcomes these limitations. Approach: We designed a model and implemented a prototype system to support open programming language interpreters. The implementation is integrated in the Neverlang framework which now exposes the structure, behaviour and the runtime state of any Neverlang-based interpreter with the ability to modify it. Knowledge: Our system provides a complete control over interpreter’s structure, behaviour and its runtime state. The approach is applicable to every Neverlang-based interpreter. Adaptation code can potentially be reused across different language implementations. Grounding: Having a prototype implementation we focused on feasibility evaluation. The paper shows that our approach well addresses problems commonly found in the research literature. We have a demon- strative video and examples that illustrate our approach on dynamic software adaptation, aspect-oriented programming, debugging and context-aware interpreters. Importance: Our paper presents the first reflective approach targeting a general framework for language development. -

A Hybrid Approach of Compiler and Interpreter Achal Aggarwal, Dr
International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 1022 ISSN 2229-5518 A Hybrid Approach of Compiler and Interpreter Achal Aggarwal, Dr. Sunil K. Singh, Shubham Jain Abstract— This paper essays the basic understanding of compiler and interpreter and identifies the need of compiler for interpreted languages. It also examines some of the recent developments in the proposed research. Almost all practical programs today are written in higher-level languages or assembly language, and translated to executable machine code by a compiler and/or assembler and linker. Most of the interpreted languages are in demand due to their simplicity but due to lack of optimization, they require comparatively large amount of time and space for execution. Also there is no method for code minimization; the code size is larger than what actually is needed due to redundancy in code especially in the name of identifiers. Index Terms— compiler, interpreter, optimization, hybrid, bandwidth-utilization, low source-code size. —————————— —————————— 1 INTRODUCTION order to reduce the complexity of designing and building • Compared to machine language, the notation used by Icomputers, nearly all of these are made to execute relatively programming languages closer to the way humans simple commands (but do so very quickly). A program for a think about problems. computer must be built by combining some very simple com- • The compiler can spot some obvious programming mands into a program in what is called machine language. mistakes. Since this is a tedious and error prone process most program- • Programs written in a high-level language tend to be ming is, instead, done using a high-level programming lan- shorter than equivalent programs written in machine guage. -
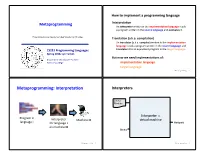
Metaprogramming: Interpretaaon Interpreters
How to implement a programming language Metaprogramming InterpretaAon An interpreter wriDen in the implementaAon language reads a program wriDen in the source language and evaluates it. These slides borrow heavily from Ben Wood’s Fall ‘15 slides. TranslaAon (a.k.a. compilaAon) An translator (a.k.a. compiler) wriDen in the implementaAon language reads a program wriDen in the source language and CS251 Programming Languages translates it to an equivalent program in the target language. Spring 2018, Lyn Turbak But now we need implementaAons of: Department of Computer Science Wellesley College implementaAon language target language Metaprogramming 2 Metaprogramming: InterpretaAon Interpreters Source Program Interpreter = Program in Interpreter Machine M virtual machine language L for language L Output on machine M Data Metaprogramming 3 Metaprogramming 4 Metaprogramming: TranslaAon Compiler C Source x86 Target Program C Compiler Program if (x == 0) { cmp (1000), $0 Program in Program in x = x + 1; bne L language A } add (1000), $1 A to B translator language B ... L: ... x86 Target Program x86 computer Output Interpreter Machine M Thanks to Ben Wood for these for language B Data and following pictures on machine M Metaprogramming 5 Metaprogramming 6 Interpreters vs Compilers Java Compiler Interpreters No work ahead of Lme Source Target Incremental Program Java Compiler Program maybe inefficient if (x == 0) { load 0 Compilers x = x + 1; ifne L } load 0 All work ahead of Lme ... inc See whole program (or more of program) store 0 Time and resources for analysis and opLmizaLon L: ... (compare compiled C to compiled Java) Metaprogramming 7 Metaprogramming 8 Compilers... whose output is interpreted Interpreters.. -

Bioinformatics: a Practical Guide to the Analysis of Genes and Proteins, Second Edition Andreas D
BIOINFORMATICS A Practical Guide to the Analysis of Genes and Proteins SECOND EDITION Andreas D. Baxevanis Genome Technology Branch National Human Genome Research Institute National Institutes of Health Bethesda, Maryland USA B. F. Francis Ouellette Centre for Molecular Medicine and Therapeutics Children’s and Women’s Health Centre of British Columbia University of British Columbia Vancouver, British Columbia Canada A JOHN WILEY & SONS, INC., PUBLICATION New York • Chichester • Weinheim • Brisbane • Singapore • Toronto BIOINFORMATICS SECOND EDITION METHODS OF BIOCHEMICAL ANALYSIS Volume 43 BIOINFORMATICS A Practical Guide to the Analysis of Genes and Proteins SECOND EDITION Andreas D. Baxevanis Genome Technology Branch National Human Genome Research Institute National Institutes of Health Bethesda, Maryland USA B. F. Francis Ouellette Centre for Molecular Medicine and Therapeutics Children’s and Women’s Health Centre of British Columbia University of British Columbia Vancouver, British Columbia Canada A JOHN WILEY & SONS, INC., PUBLICATION New York • Chichester • Weinheim • Brisbane • Singapore • Toronto Designations used by companies to distinguish their products are often claimed as trademarks. In all instances where John Wiley & Sons, Inc., is aware of a claim, the product names appear in initial capital or ALL CAPITAL LETTERS. Readers, however, should contact the appropriate companies for more complete information regarding trademarks and registration. Copyright ᭧ 2001 by John Wiley & Sons, Inc. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic or mechanical, including uploading, downloading, printing, decompiling, recording or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without the prior written permission of the Publisher. -

From Interpreter to Compiler and Virtual Machine: a Functional Derivation Basic Research in Computer Science
BRICS Basic Research in Computer Science BRICS RS-03-14 Ager et al.: From Interpreter to Compiler and Virtual Machine: A Functional Derivation From Interpreter to Compiler and Virtual Machine: A Functional Derivation Mads Sig Ager Dariusz Biernacki Olivier Danvy Jan Midtgaard BRICS Report Series RS-03-14 ISSN 0909-0878 March 2003 Copyright c 2003, Mads Sig Ager & Dariusz Biernacki & Olivier Danvy & Jan Midtgaard. BRICS, Department of Computer Science University of Aarhus. All rights reserved. Reproduction of all or part of this work is permitted for educational or research use on condition that this copyright notice is included in any copy. See back inner page for a list of recent BRICS Report Series publications. Copies may be obtained by contacting: BRICS Department of Computer Science University of Aarhus Ny Munkegade, building 540 DK–8000 Aarhus C Denmark Telephone: +45 8942 3360 Telefax: +45 8942 3255 Internet: [email protected] BRICS publications are in general accessible through the World Wide Web and anonymous FTP through these URLs: http://www.brics.dk ftp://ftp.brics.dk This document in subdirectory RS/03/14/ From Interpreter to Compiler and Virtual Machine: a Functional Derivation Mads Sig Ager, Dariusz Biernacki, Olivier Danvy, and Jan Midtgaard BRICS∗ Department of Computer Science University of Aarhusy March 2003 Abstract We show how to derive a compiler and a virtual machine from a com- positional interpreter. We first illustrate the derivation with two eval- uation functions and two normalization functions. We obtain Krivine's machine, Felleisen et al.'s CEK machine, and a generalization of these machines performing strong normalization, which is new. -

Ahs: Automatic Heterogeneous Supercomputing) H
Purdue University Purdue e-Pubs ECE Technical Reports Electrical and Computer Engineering 1-1-1993 WOULD YOU RUN IT HERE ... OR THERE? (AHS: AUTOMATIC HETEROGENEOUS SUPERCOMPUTING) H. G. Dietz Purdue University School of Electrical Engineering W. E. Cohen Purdue University School of Electrical Engineering B. K. Grant Purdue University School of Electrical Engineering Follow this and additional works at: http://docs.lib.purdue.edu/ecetr Dietz, H. G.; Cohen, W. E.; and Grant, B. K., "WOULD YOU RUN IT HERE ... OR THERE? (AHS: AUTOMATIC HETEROGENEOUS SUPERCOMPUTING)" (1993). ECE Technical Reports. Paper 216. http://docs.lib.purdue.edu/ecetr/216 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. WOULD YOU RUN IT HERE... OR THERE? (AHS: AUTOMATIC HETEROGENEOUS SUPERCOMPUTING) TR-EE 93-5 JANUARY 1993 AHS: Auto Heterogeneous Supercomputing Table of Contents 1. Introducxion .......................................................................................................................... 2. The MIlbiX Language ........................................................................................................ 2.1. Syntax .................................................................................................................... 2.2. Data Declarations ................................................................................................... 2.3. Communication And Synchmnization .................................................................. -

Multi-Threading in IDL
Multi-Threading in IDL Copyright © 2001-2007 ITT Visual Information Solutions All Rights Reserved http://www.ittvis.com/ IDL® is a registered trademark of ITT Visual Information Solutions for the computer software described herein and its associated documentation. All other product names and/or logos are trademarks of their respective owners. Multi-Threading in IDL Table of Contents I. Introduction 3 Introduction to Multi-Threading in IDL 3 What is Multi-Threading? 3 Why Apply Multi-Threading to IDL? 5 A Related Concept: Distributed Processing 5 II. The Thread Pool 7 Design and Implementation of the Thread Pool 7 The IDL Thread Pool 7 Why The Thread Pool Beats Alternatives 9 Re-Architecture of IDL 9 Automatically Parallelizing Compilers 10 Threading at the User Level 11 III. Performance of the Thread Pool 13 Your Mileage May Vary 13 Amdahl’s Law 13 Interpreting TIME_THREAD Plots 15 Example System Results 17 Platform Comparisons 31 IV. Conclusions 36 Summary 36 Advice (So What Should I Buy?) 37 V. Appendices 39 Appendix A: IDL Routines that use the Thread Pool 39 Appendix B: Additional Benchmark Results 41 Appendix C: Glossary 53 ITT Visual Information Solutions • 4990 Pearl East Circle Boulder, CO 80301 P: 303.786.9900 • F: 303.786.9909 • www.ittvis.com Page 2 of 54 Multi-Threading in IDL Introduction Introduction to Multi-Threading in IDL ITT-VIS has added support for using threads internally in IDL to accelerate specific numerical computations on multi-processor systems. Multi-processor capable hardware has finally become cheap and widely available. Most operating systems have support for SMP (Symmetric Multi-Processing), and IDL users are beginning to own such hardware. -

Programming, Languages
Programming, Languages A programming language is a language; an abstraction of thought applied to a specific domain. Alan Turing pioneered the idea of a programming language in his 1936 paper “On Computable Numbers, with an Application to the Entscheidungsproblem”. There he developed the idea of a notational system that could represent any other system by writing, erasing and storing a limited number of symbols; a 'universal computing machine'. Programming, Languages A programming language is a way to abstract the features of a problem from the implementation of the solution. It is a way of telling a machine what to do. The need to precisely tell a computer what to do and the desire to make the instructions easily readable to a human being are difficult to reconcile. Today, programming languages are used and developed mostly for specific applications, but research continues into novel forms of thought representation. Programming languages have also entered the cultural domain. With the ability to wrestle with the language in which they are written, just as much contemporary literature does, programming languages are recognized as a form of cultural expression. Programming, Languages The only language that a computer can understand is machine language. Machine language is of a set of basic operations whose execution is implemented in the hardware of the processor. High level programming languages provide a machine-independent level of abstraction that is higher than the machine language. They are more adapted to a human-machine interaction. But this also implies that there is a sort of translator between the high level programming language and the machine languages. -

Programming with a Differentiable Forth Interpreter
Programming with a Differentiable Forth Interpreter Matko Bosnjakˇ 1 Tim Rocktaschel¨ 2 Jason Naradowsky 3 Sebastian Riedel 1 Abstract partial procedural background knowledge: one may know the rough structure of the program, or how to implement Given that in practice training data is scarce for all but a small set of problems, a core question is how to incorporate several subroutines that are likely necessary to solve the prior knowledge into a model. In this paper, we consider task. For example, in programming by demonstration (Lau the case of prior procedural knowledge for neural networks, et al., 2001) or query language programming (Neelakantan such as knowing how a program should traverse a sequence, et al., 2015a) a user establishes a larger set of conditions on but not what local actions should be performed at each the data, and the model needs to set out the details. In all step. To this end, we present an end-to-end differentiable interpreter for the programming language Forth which these scenarios, the question then becomes how to exploit enables programmers to write program sketches with slots various types of prior knowledge when learning algorithms. that can be filled with behaviour trained from program input-output data. We can optimise this behaviour directly To address the above question we present an approach that through gradient descent techniques on user-specified enables programmers to inject their procedural background objectives, and also integrate the program into any larger knowledge into a neural network. In this approach, the neural computation graph. We show empirically that our programmer specifies a program sketch (Solar-Lezama interpreter is able to effectively leverage different levels et al., 2005) in a traditional programming language. -

Programming Paradigms Compilation Or Interpretation
Programming Computer programming is the iterative process of writing or editing source code. Editing source code involves testing, analyzing, and refining, and sometimes coordinating with other programmers on a jointly developed program. A person who practices this skill is referred to as a computer programmer, software developer or coder. The sometimes lengthy process of computer programming is usually referred to as software development. The term software engineering is becoming popular as the process is seen as an engineering discipline. Paradigms Computer programs can be categorized by the programming language paradigm used to produce them. Two of the main paradigms are imperative and declarative. Programs written using an imperative language specify an algorithm using declarations, expressions, and statements. A declaration couples a variable name to a datatype. For example: var x: integer; . An expression yields a value. For example: 2 + 2 yields 4. Finally, a statement might assign an expression to a variable or use the value of a variable to alter the program's control flow. For example: x := 2 + 2; if x = 4 then do_something(); One criticism of imperative languages is the side effect of an assignment statement on a class of variables called non-local variables. Programs written using a declarative language specify the properties that have to be met by the output. They do not specify details expressed in terms of the control flow of the executing machine but of the mathematical relations between the declared objects and their properties. Two broad categories of declarative languages are functional languages and logical languages. The principle behind functional languages (like Haskell) is to not allow side effects, which makes it easier to reason about programs like mathematical functions. -

The Bioperl Toolkit: Perl Modules for the Life Sciences
Resource The Bioperl Toolkit: Perl Modules for the Life Sciences Jason E. Stajich,1,18,19 David Block,2,18 Kris Boulez,3 Steven E. Brenner,4 Stephen A. Chervitz,# Chris Dagdigian,% Georg Fuellen,( James G.R. Gilbert,8 Ian Korf,9 Hilmar Lapp,10 Heikki Lehva1slaiho,11 Chad Matsalla,12 Chris J. Mungall,13 Brian I. Osborne,14 Matthew R. Pocock,8 Peter Schattner,15 Martin Senger,11 Lincoln D. Stein,16 Elia Stupka,17 Mark D. Wilkinson,2 and Ewan Birney11 1University Program in Genetics, Duke University, Durham, North Carolina 27710, USA; 2National Research Council of Canada, Plant Biotechnology Institute, Saskatoon, SK S7N &'( Canada; )AlgoNomics, # 9052 Gent, Belgium; +Department of Plant and Molecular Biology, University of California, Berkeley, California 94720, USA; *Affymetrix, Inc., Emeryville, California 94608, USA; 1Open Bioinformatics Foundation, Somerville, Massachusetts 02144, USA; 7Integrated Functional Genomics, IZKF, University Hospital Muenster, 48149 Muenster, Germany; 2The Welcome Trust Sanger Institute, Welcome Trust Genome Campus, Hinxton, Cambridge, CB10 1SA UK; (Department of Computer Science, Washington University, St. Louis, Missouri 63130, USA; 10Genomics Institute of the Novartis Research Foundation (GNF), San Diego, California 92121, USA; 11European Bioinformatics Institute, Welcome Trust Genome Campus, Hinxton, Cambridge CB10 1SD UK; 12Agriculture and Agri-Food Canada, Saskatoon Research Centre, Saskatoon SK, S7N 0X2 Canada; 13Berkeley Drosophila Genome Project, University of California, Berkeley, California 94720,