Simple Graphs and Trees Benjamin Cosman, Patrick Lin and Mahesh Viswanathan Fall 2020
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
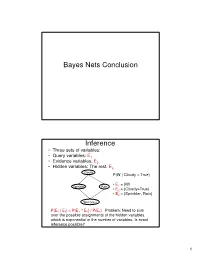
Bayes Nets Conclusion Inference
Bayes Nets Conclusion Inference • Three sets of variables: • Query variables: E1 • Evidence variables: E2 • Hidden variables: The rest, E3 Cloudy P(W | Cloudy = True) • E = {W} Sprinkler Rain 1 • E2 = {Cloudy=True} • E3 = {Sprinkler, Rain} Wet Grass P(E 1 | E 2) = P(E 1 ^ E 2) / P(E 2) Problem: Need to sum over the possible assignments of the hidden variables, which is exponential in the number of variables. Is exact inference possible? 1 A Simple Case A B C D • Suppose that we want to compute P(D = d) from this network. A Simple Case A B C D • Compute P(D = d) by summing the joint probability over all possible values of the remaining variables A, B, and C: P(D === d) === ∑∑∑ P(A === a, B === b,C === c, D === d) a,b,c 2 A Simple Case A B C D • Decompose the joint by using the fact that it is the product of terms of the form: P(X | Parents(X)) P(D === d) === ∑∑∑ P(D === d | C === c)P(C === c | B === b)P(B === b | A === a)P(A === a) a,b,c A Simple Case A B C D • We can avoid computing the sum for all possible triplets ( A,B,C) by distributing the sums inside the product P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a 3 A Simple Case A B C D This term depends only on B and can be written as a 2- valued function fA(b) P(D === d) === ∑∑∑ P(D === d | C === c)∑∑∑P(C === c | B === b)∑∑∑P(B === b| A === a)P(A === a) c b a A Simple Case A B C D This term depends only on c and can be written as a 2- valued function fB(c) === === === === === === P(D d) ∑∑∑ P(D d | C c)∑∑∑P(C c | B b)f A(b) c b …. -

Tree Structures
Tree Structures Definitions: o A tree is a connected acyclic graph. o A disconnected acyclic graph is called a forest o A tree is a connected digraph with these properties: . There is exactly one node (Root) with in-degree=0 . All other nodes have in-degree=1 . A leaf is a node with out-degree=0 . There is exactly one path from the root to any leaf o The degree of a tree is the maximum out-degree of the nodes in the tree. o If (X,Y) is a path: X is an ancestor of Y, and Y is a descendant of X. Root X Y CSci 1112 – Algorithms and Data Structures, A. Bellaachia Page 1 Level of a node: Level 0 or 1 1 or 2 2 or 3 3 or 4 Height or depth: o The depth of a node is the number of edges from the root to the node. o The root node has depth zero o The height of a node is the number of edges from the node to the deepest leaf. o The height of a tree is a height of the root. o The height of the root is the height of the tree o Leaf nodes have height zero o A tree with only a single node (hence both a root and leaf) has depth and height zero. o An empty tree (tree with no nodes) has depth and height −1. o It is the maximum level of any node in the tree. CSci 1112 – Algorithms and Data Structures, A. -

A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width
Introduction Preliminary Definitions Pathwidth Algorithm Summary A Simple Linear-Time Algorithm for Finding Path-Decompostions of Small Width Kevin Cattell Michael J. Dinneen Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. Canada V8W 3P6 Information Processing Letters 57 (1996) 197–203 Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Pathwidth Algorithm Summary Outline 1 Introduction Motivation History 2 Preliminary Definitions Boundaried graphs Path-decompositions Topological tree obstructions 3 Pathwidth Algorithm Main result Linear-time algorithm Proof of correctness Other results Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary Motivation Pathwidth is related to several VLSI layout problems: vertex separation link gate matrix layout edge search number ... Usefullness of bounded treewidth in: study of graph minors (Robertson and Seymour) input restrictions for many NP-complete problems (fixed-parameter complexity) Kevin Cattell, Michael J. Dinneen, Michael R. Fellows Linear-Time Path-Decomposition Algorithm Introduction Preliminary Definitions Motivation Pathwidth Algorithm History Summary History General problem(s) is NP-complete Input: Graph G, integer t Question: Is tree/path-width(G) ≤ t? Algorithmic development (fixed t): O(n2) nonconstructive treewidth algorithm by Robertson and Seymour (1986) O(nt+2) treewidth algorithm due to Arnberg, Corneil and Proskurowski (1987) O(n log n) treewidth algorithm due to Reed (1992) 2 O(2t n) treewidth algorithm due to Bodlaender (1993) O(n log2 n) pathwidth algorithm due to Ellis, Sudborough and Turner (1994) Kevin Cattell, Michael J. Dinneen, Michael R. -

Blast Domination for Mycielski's Graph of Graphs
International Journal of Engineering and Advanced Technology (IJEAT) ISSN: 2249 – 8958, Volume-8, Issue-6S3, September 2019 Blast Domination for Mycielski’s Graph of Graphs K. Ameenal Bibi, P.Rajakumari AbstractThe hub of this article is a search on the behavior of is the minimum cardinality of a distance-2 dominating set in the Blast domination and Blast distance-2 domination for 퐺. Mycielski’s graph of some particular graphs and zero divisor graphs. Definition 2.3[7] A non-empty subset 퐷 of 푉 of a connected graph 퐺 is Key Words:Blast domination number, Blast distance-2 called a Blast dominating set, if 퐷 is aconnected dominating domination number, Mycielski’sgraph. set and the induced sub graph < 푉 − 퐷 >is triple connected. The minimum cardinality taken over all such Blast I. INTRODUCTION dominating sets is called the Blast domination number of The concept of triple connected graphs was introduced by 퐺and is denoted by tc . Paulraj Joseph et.al [9]. A graph is said to be triple c (G) connected if any three vertices lie on a path in G. In [6] the Definition2.4 authors introduced triple connected domination number of a graph. A subset D of V of a nontrivial graph G is said to A non-empty subset 퐷 of vertices in a graph 퐺 is a blast betriple connected dominating set, if D is a dominating set distance-2 dominating set if every vertex in 푉 − 퐷 is within and <D> is triple connected. The minimum cardinality taken distance-2 of atleast one vertex in 퐷. -

Determination and Testing the Domination Numbers of Tadpole Graph, Book Graph and Stacked Book Graph Using MATLAB Ayhan A
College of Basic Education Researchers Journal Vol. 10, No. 1 Determination and Testing the Domination Numbers of Tadpole Graph, Book Graph and Stacked Book Graph Using MATLAB Ayhan A. khalil Omar A.Khalil Technical College of Mosul -Foundation of Technical Education Received: 11/4/2010 ; Accepted: 24/6/2010 Abstract: A set is said to be dominating set of G if for every there exists a vertex such that . The minimum cardinality of vertices among dominating set of G is called the domination number of G denoted by . We investigate the domination number of Tadpole graph, Book graph and Stacked Book graph. Also we test our theoretical results in computer by introducing a matlab procedure to find the domination number , dominating set S and draw this graph that illustrates the vertices of domination this graphs. It is proved that: . Keywords: Dominating set, Domination number, Tadpole graph, Book graph, stacked graph. إﯾﺟﺎد واﺧﺗﺑﺎر اﻟﻌدد اﻟﻣﮭﯾﻣن(اﻟﻣﺳﯾطر)Domination number ﻟﻠﺑﯾﺎﻧﺎت ﺗﺎدﺑول (Tadpole graph)، ﺑﯾﺎن ﺑوك (Book graph) وﺑﯾﺎن ﺳﺗﺎﻛﯾت ﺑوك (Stacked Book graph) ﺑﺎﺳﺗﻌﻣﺎل اﻟﻣﺎﺗﻼب أﯾﮭﺎن اﺣﻣد ﺧﻠﯾل ﻋﻣر اﺣﻣد ﺧﻠﯾل اﻟﻛﻠﯾﺔ اﻟﺗﻘﻧﯾﺔ-ﻣوﺻل- ھﯾﺋﺔ اﻟﺗﻌﻠﯾم اﻟﺗﻘﻧﻲ ﻣﻠﺧص اﻟﺑﺣث : ﯾﻘﺎل ﻷﯾﺔ ﻣﺟﻣوﻋﺔ ﺟزﺋﯾﺔ S ﻣن ﻣﺟﻣوﻋﺔ اﻟرؤوس V ﻓﻲ ﺑﯾﺎن G ﺑﺄﻧﻬﺎ ﻣﺟﻣوﻋﺔ ﻣﻬﯾﻣﻧﺔ Dominating set إذا ﻛﺎن ﻟﻛل أرس v ﻓﻲ اﻟﻣﺟﻣوﻋﺔ V-S ﯾوﺟد أرس u ﻓﻲS ﺑﺣﯾث uv ﺿﻣن 491 Ayhan A. & Omar A. ﺣﺎﻓﺎت اﻟﺑﯾﺎن،. وﯾﻌرف اﻟﻌدد اﻟﻣﻬﯾﻣن Domination number ﺑﺄﻧﻪ أﺻﻐر ﻣﺟﻣوﻋﺔ أﺳﺎﺳﯾﺔ ﻣﻬﯾﻣﻧﺔ Domination. ﻓﻲ ﻫذا اﻟﺑﺣث ﺳوف ﻧدرس اﻟﻌدد اﻟﻣﻬﯾﻣن Domination number ﻟﺑﯾﺎن ﺗﺎدﺑول (Tadpole graph) ، ﺑﯾﺎن ﺑوك (Book graph) وﺑﯾﺎن ﺳﺗﺎﻛﯾت ﺑوك ( Stacked Book graph). -

Lowest Common Ancestors in Trees and Directed Acyclic Graphs1
Lowest Common Ancestors in Trees and Directed Acyclic Graphs1 Michael A. Bender2 3 Martín Farach-Colton4 Giridhar Pemmasani2 Steven Skiena2 5 Pavel Sumazin6 Version: We study the problem of finding lowest common ancestors (LCA) in trees and directed acyclic graphs (DAGs). Specifically, we extend the LCA problem to DAGs and study the LCA variants that arise in this general setting. We begin with a clear exposition of Berkman and Vishkin’s simple optimal algorithm for LCA in trees. The ideas presented are not novel theoretical contributions, but they lay the foundation for our work on LCA problems in DAGs. We present an algorithm that finds all-pairs-representative : LCA in DAGs in O~(n2 688 ) operations, provide a transitive-closure lower bound for the all-pairs-representative-LCA problem, and develop an LCA-existence algorithm that preprocesses the DAG in transitive-closure time. We also present a suboptimal but practical O(n3) algorithm for all-pairs-representative LCA in DAGs that uses ideas from the optimal algorithms in trees and DAGs. Our results reveal a close relationship between the LCA, all-pairs-shortest-path, and transitive-closure problems. We conclude the paper with a short experimental study of LCA algorithms in trees and DAGs. Our experiments and source code demonstrate the elegance of the preprocessing-query algorithms for LCA in trees. We show that for most trees the suboptimal Θ(n log n)-preprocessing Θ(1)-query algorithm should be preferred, and demonstrate that our proposed O(n3) algorithm for all- pairs-representative LCA in DAGs performs well in both low and high density DAGs. -

Trees a Tree Is a Graph Which Is (A) Connected and (B) Has No Cycles (Acyclic)
Trees A tree is a graph which is (a) Connected and (b) has no cycles (acyclic). 1 Lemma 1 Let the components of G be C1; C2; : : : ; Cr, Suppose e = (u; v) 2= E, u 2 Ci; v 2 Cj. (a) i = j ) !(G + e) = !(G). (b) i 6= j ) !(G + e) = !(G) − 1. (a) v u (b) u v 2 Proof Every path P in G + e which is not in G must contain e. Also, !(G + e) ≤ !(G): Suppose (x = u0; u1; : : : ; uk = u; uk+1 = v; : : : ; u` = y) is a path in G + e that uses e. Then clearly x 2 Ci and y 2 Cj. (a) follows as now no new relations x ∼ y are added. (b) Only possible new relations x ∼ y are for x 2 Ci and y 2 Cj. But u ∼ v in G + e and so Ci [ Cj becomes (only) new component. 2 3 Lemma 2 G = (V; E) is acyclic (forest) with (tree) components C1; C2; : : : ; Ck. jV j = n. e = (u; v) 2= E, u 2 Ci; v 2 Cj. (a) i = j ) G + e contains a cycle. (b) i 6= j ) G + e is acyclic and has one less com- ponent. (c) G has n − k edges. 4 (a) u; v 2 Ci implies there exists a path (u = u0; u1; : : : ; u` = v) in G. So G + e contains the cycle u0; u1; : : : ; u`; u0. u v 5 (a) v u Suppose G + e contains the cycle C. e 2 C else C is a cycle of G. C = (u = u0; u1; : : : ; u` = v; u0): But then G contains the path (u0; u1; : : : ; u`) from u to v – contradiction. -

Constructing Arbitrarily Large Graphs with a Specified Number Of
Electronic Journal of Graph Theory and Applications 4 (1) (2019), 1–8 Constructing Arbitrarily Large Graphs with a Specified Number of Hamiltonian Cycles Michael Haythorpea aSchool of Computer Science, Engineering and Mathematics, Flinders University, 1284 South Road, Clovelly Park, SA 5042, Australia michael.haythorpe@flinders.edu.au Abstract A constructive method is provided that outputs a directed graph which is named a broken crown graph, containing 5n − 9 vertices and k Hamiltonian cycles for any choice of integers n ≥ k ≥ 4. The construction is not designed to be minimal in any sense, but rather to ensure that the graphs produced remain non-trivial instances of the Hamiltonian cycle problem even when k is chosen to be much smaller than n. Keywords: Hamiltonian cycles, Graph Construction, Broken Crown Mathematics Subject Classification : 05C45 1. Introduction The Hamiltonian cycle problem (HCP) is a famous NP-complete problem in which one must determine whether a given graph contains a simple cycle traversing all vertices of the graph, or not. Such a simple cycle is called a Hamiltonian cycle (HC), and a graph containing at least one arXiv:1902.10351v1 [math.CO] 27 Feb 2019 Hamiltonian cycle is said to be a Hamiltonian graph. Typically, randomly generated graphs (such as Erdos-R˝ enyi´ graphs), if connected, are Hamil- tonian and contain many Hamiltonian cycles. Although HCP is an NP-complete problem, for these graphs it is often fairly easy for a sophisticated heuristic (e.g. see Concorde [1], Keld Helsgaun’s LKH [4] or Snakes-and-ladders Heuristic [2]) to discover one of the multitude of Hamiltonian cy- cles through a clever search. -
![Arxiv:1901.04560V1 [Math.CO] 14 Jan 2019 the flexibility That Makes Hypergraphs Such a Versatile Tool Complicates Their Analysis](https://docslib.b-cdn.net/cover/7775/arxiv-1901-04560v1-math-co-14-jan-2019-the-exibility-that-makes-hypergraphs-such-a-versatile-tool-complicates-their-analysis-817775.webp)
Arxiv:1901.04560V1 [Math.CO] 14 Jan 2019 the flexibility That Makes Hypergraphs Such a Versatile Tool Complicates Their Analysis
MINIMALLY CONNECTED HYPERGRAPHS MARK BUDDEN, JOSH HILLER, AND ANDREW PENLAND Abstract. Graphs and hypergraphs are foundational structures in discrete mathematics. They have many practical applications, including the rapidly developing field of bioinformatics, and more generally, biomathematics. They are also a source of interesting algorithmic problems. In this paper, we define a construction process for minimally connected r-uniform hypergraphs, which captures the intuitive notion of building a hypergraph piece-by-piece, and a numerical invariant called the tightness, which is independent of the construc- tion process used. Using these tools, we prove some fundamental properties of minimally connected hypergraphs. We also give bounds on their chromatic numbers and provide some results involving edge colorings. We show that ev- ery connected r-uniform hypergraph contains a minimally connected spanning subhypergraph and provide a polynomial-time algorithm for identifying such a subhypergraph. 1. Introduction Graphs and hypergraphs provide many beautiful results in discrete mathemat- ics. They are also extremely useful in applications. Over the last six decades, graphs and their generalizations have been used for modeling many biological phenomena, ranging in scale from protein-protein interactions, individualized cancer treatments, carcinogenesis, and even complex interspecial relationships [12, 15, 16, 19, 22]. In the last few years in particular, hypergraphs have found an increasingly prominent position in the biomathematical literature, as they allow scientists and practitioners to model complex interactions between arbitrarily many actors [22]. arXiv:1901.04560v1 [math.CO] 14 Jan 2019 The flexibility that makes hypergraphs such a versatile tool complicates their analysis. Because of this, many different algorithms and metrics have been devel- oped to assist with their application [18, 23]. -

Dominating Cycles in Halin Graphs*
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Discrete Mathematics 86 (1990) 215-224 215 North-Holland DOMINATING CYCLES IN HALIN GRAPHS* Mirosiawa SKOWRONSKA Institute of Mathematics, Copernicus University, Chopina 12/18, 87-100 Torun’, Poland Maciej M. SYStO Institute of Computer Science, University of Wroclaw, Przesmyckiego 20, 51-151 Wroclaw, Poland Received 2 December 1988 A cycle in a graph is dominating if every vertex lies at distance at most one from the cycle and a cycle is D-cycle if every edge is incident with a vertex of the cycle. In this paper, first we provide recursive formulae for finding a shortest dominating cycle in a Hahn graph; minor modifications can give formulae for finding a shortest D-cycle. Then, dominating cycles and D-cycles in a Halin graph H are characterized in terms of the cycle graph, the intersection graph of the faces of H. 1. Preliminaries The various domination problems have been extensively studied. Among them is the problem whether a graph has a dominating cycle. All graphs in this paper have no loops and multiple edges. A dominating cycle in a graph G = (V(G), E(G)) is a subgraph C of G which is a cycle and every vertex of V(G) \ V(C) is adjacent to a vertex of C. There are graphs which have no dominating cycles, and moreover, determining whether a graph has a dominating cycle on at most 1 vertices is NP-complete even in the class of planar graphs [7], chordal, bipartite and split graphs [3]. -

Section 11.1 Introduction to Trees Definition
Section 11.1 Introduction to Trees Definition: A tree is a connected undirected graph with no simple circuits. : A circuit is a path of length >=1 that begins and ends a the same vertex. d d Tournament Trees A common form of tree used in everyday life is the tournament tree, used to describe the outcome of a series of games, such as a tennis tournament. Alice Antonia Alice Anita Alice Abigail Abigail Alice Amy Agnes Agnes Angela Angela Angela Audrey A Family Tree Much of the tree terminology derives from family trees. Gaea Ocean Cronus Phoebe Zeus Poseidon Demeter Pluto Leto Iapetus Persephone Apollo Atlas Prometheus Ancestor Tree An inverted family tree. Important point - it is a binary tree. Iphigenia Clytemnestra Agamemnon Leda Tyndareus Aerope Atreus Catreus Forest Graphs containing no simple circuits that are not connected, but each connected component is a tree. Theorem An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices. Rooted Trees Once a vertex of a tree has been designated as the root of the tree, it is possible to assign direction to each of the edges. Rooted Trees g a e f e c b b d a d c g f root node a internal vertex parent of g b c d e f g leaf siblings h i a b c d e f g h i h i ancestors of and a b c d e f g subtree with b as its h i root subtree with c as its root m-ary trees A rooted tree is called an m-ary tree if every internal vertex has no more than m children. -

On the Number of Cycles in a Graph with Restricted Cycle Lengths
On the number of cycles in a graph with restricted cycle lengths D´anielGerbner,∗ Bal´azsKeszegh,y Cory Palmer,z Bal´azsPatk´osx October 12, 2016 Abstract Let L be a set of positive integers. We call a (directed) graph G an L-cycle graph if all cycle lengths in G belong to L. Let c(L; n) be the maximum number of cycles possible in an n-vertex L-cycle graph (we use ~c(L; n) for the number of cycles in directed graphs). In the undirected case we show that for any fixed set L, we have k=` c(L; n) = ΘL(nb c) where k is the largest element of L and 2` is the smallest even element of L (if L contains only odd elements, then c(L; n) = ΘL(n) holds.) We also give a characterization of L-cycle graphs when L is a single element. In the directed case we prove that for any fixed set L we have ~c(L; n) = (1 + n 1 k 1 o(1))( k−1 ) − , where k is the largest element of L. We determine the exact value of ~c(fkg; n−) for every k and characterize all graphs attaining this maximum. 1 Introduction In this paper we examine graphs that contain only cycles of some prescribed lengths (where the length of a cycle or a path is the number of its edges). Let L be a set of positive integers. We call a graph G an L-cycle graph if all cycle lengths in G belong to L.