DOCSLIB.ORG

RR Lyrae Light Curve Decomposition and the Oosterhoff Dichotomy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
RR Lyrae Light Curve Decomposition and the Oosterhoff Dichotomy RR Lyrae light curve decomposition and the Oosterhoff dichotomy A. Arellano Ferro Instituto de Astronomía Universidad Nacional Autónoma de México collaborators: Sunetra Giridhar, IIA, India Carlos Lázaro; M.J. Arévalo, IAC, Spain Victoria Rojas, IA-UNAM, México P. Rosenzweig; G. García Lugo, U. Los Andes, Venezuela Daniel Bramich; Cambridge University, UK Indian Institute of Astrophysics may 2006 The Oosterhoff types of clusters Oosterhoff (1930) The Observatory, 62, 104. noticed that periods of RR Lyraes differe and are grouped in two families: Oo I <Pab>=0.55 d <Pc>=0.32d Oo II <Pab>=0.64 d <Pc>=0.36d Oo II's are more metal poor that Oo I's and Oo II's have higher rate of RRc's than Oo I's Diagramas C-M de NGC 6934 Kaluzny, Olech & Stanek, 2001, ApJ, 121, 1533 Evolution of the Horizontal Branch (Rood 1973, ApJ 184, 815) M3 The metallicities and distances of the globular clusters are of Globular Cluster relevance in the contexts stellar evolution and galactic dynamics. The structure of the Horizontal Branch (HB) and the role of metallicity can be studied in detail if accurate metallicities, temperatures and luminosities can be determined. PROBLEM: Accurate metallicities from high resolution spectroscopy do exist for stars with V~ 11-12 In the HB V~13.5 for the nearest clusters. Only very recently, with telescope of the 8m–10m-class, good results can be obtained for V~16-17 mag. with good S/N (e.g. James et al. 2004 Astron. Astrophys., 427, 825-838 (2004) for NGC 6752 (others examples see next slide) • Gratton , et al. (2005) Astron. Astrophys., 440, 901-908 NGCHigh 6752: ResolutionFLAMES at VLT2 allowe ind Globularto obtain spectra centred Clusters: on Hα at a resolutionsome of examplesR=6000 and 5<S/N<50 for 120 stars near the turn-off with GIRAFFE from a single 1300 seconds exposure. The same exposure provided UVES spectra of seven stars near the red giant branch bump at a resolution of 40000 and 20<S/N<40. • Yong et al. (2005) Astron. Astrophys., 438, 875-888 Elemental abundance ratios [X/Fe] for 20 elements in 38 bright giants of NGC 6752 with UVES on the VLT at resolutions 110 000 and 60 000 with S/N = 250-150 • Cohen & Melendez, (2005) Astron. J., 129, 303-329 38 stars distributed from the tip to the base of the red giant branch (RGB) in M3 and M13: HIRES at the Keck Observatory, with resolution of 35,000 with S/N > 75 exp times from 200 s for V~12.5 to 7500 s for V ~ 17.5 ALTERNATIVE APPROACH (more efficient, more accessible) AccurateAccurate CCDCCD PhotometryPhotometry ++ FourierFourier DescompositionDescomposition ofof lightlight curvescurves ++ SemiempiricalSemiempirical calibrationscalibrations NGC 4147 Μ2 We shall illustrate some results on these two clusters DANDIA: A differential imaging package Bramich, D. M., et al. 2005, MNRAS, 359, 1096 ● Procedure involves the matching of a high quality reference image to each image in ●the time series, by solving for a spatially-varying convolution kernel and differential ●sky background function. ●Difference images are constructed via the subtraction of the convolved reference image ●from the time series images. Photometry on the difference images yields differential ●fluxes for each star relative to the flux from the reference image. Conversion of the ●light curves to magnitudes requires an accurate measurement of the reference flux. ●We measured the stellar fluxes on the reference frame using DAOPhot (Stetson 1987). Curvas de luz de RR Lyraes en NGC 4147 V6 in NGC4147 V2 in NGC4147 V2 en M2 P= 69.7 d M2: known variables New variables in M2 RRab Known RR Lyraes in M2 RRc Light curves of new variables •Light Curve Fourier decomposition m(t) = Ao +Σ Ακ cos (2πk(t-E)/P + φκ) ●The Fourier parameters are defined as: φij=j φi-i φj Rij = Ai / Aj •The shape of the light curve can be quantified in terms of low order harmonics φ1j=j φ1 - φj R1j = A1 / Aj (j=1,2,3,4) Empirical Calibrations of Physical Parameters RRc • log M = 0.52 log P -0.11 φ31 + 0.39 • log L = 1.04 log P -0.058 φ31 + 2.41 Simon & Clement (1993) • log Teff = 3.265 -0.3026 log P - 0.1777 log M + 0.2402 + log L • log Y = -20.26 + 4.935 log Teff -0.2638 log M + 0.3318 + log L •Mv= 1.261 –0.961 P –0.044 φ21 – 4.447 A4 Kovács (1998) • [Fe/H] = 3.702 log P ^2 + 0.124 φ(c)31^2 – 0.845 φ(c)31 – 1.023 φ(c)31log P - 2.620 Morgan et al. (2005) RRab • [Fe/H] = -5.038 - 5.394 P 1.345 φ31 Jurcsik & Kovács (1996), •Mv = 1.221 -1.369 P -0.477 A1 + 0.103 φ31 Kovács & Jurcsik (1996; 1997) Jurcsik (1998) • log Teff = 3.9291 -0.1112 (V-K)o - 0.0032 [Fe/H] Results for RRc stars in M2 Results for RRab stars in M2 Determination of the radii • Given log L/Lo and Teff one can get the redius log R/Ro (LT) • Marconi et al. (2005) offer a P-R-Z relationship log Z = [Fe/H] – 1.70 + log(0.638 f + 0.362) with f being the α enhacement factor (=1 Salarsis et al. 1993). the one can determin the radius log R/Ro (PRZ) from individual measurements of [Fe/H]. RR Lyraes in M2 on the HR Diagram Instability strips: Bono et al. (1995); models Jurcsic (1998); 272 RRab’s Two luminosities for RRc’s from two calibrations. ZAHB models are from Lee & Demarque (1990). Physical parameters of globular clusters from RRc Fourier light curve decomposition Physical parameters of globular clusters from RRab Fourier light curve decomposition General trends in globular clusters from RRc stars log M/Mo = -(0.10+/-0.019)[Fe/H] - (0.381+/-0.032) log L/Lo = -(0.111+/-0.009)[Fe/H] + (1.554+/-0.016) log Teff = +(0.013+/-0.001)[Fe/H] + (3.882+/-0.002) General Trends in Globular Clusters From RRab Stars Log Teff = +(0.032+/-0.005)[Fe/H] + (3.852+/-0.008) Mv = +(0.191+/-0.037)[Fe/H] + (1.032+/-0.054) Conclusions from Globular Cluster Trends The RR Lyrae stars in Oo II clusters are: more massive more luminous cooler than in OoI clusters Thus OoII’s are more evolved than Oo I’s MMV –– [Fe/H]:[Fe/H thethe RRRR LyraeLyrae distancedistance scalescale • This correlation has been broadly studied in the past. • Evidences are given that it is not lineal (Caputo 2000) • The average relationship as obtained from assorted approaches is MV = (0.23 +/- 0.04) [Fe/H] + (0.93 +/- 0.12) (Chavoyer 1999) • Our average for the RRc and RRab in M2 is: MV = (0.22 +/- 0.03) [Fe/H] + (0.86 +/- 0.05) This relation predicts: MV = 0.53 +/- 0.08 for [Fe/H] = -1.5 • This is in good agreement with the results: MV = 0.58 +/- 0.04 (Cacciari 2003) obtained from assorted methods MV = 0.61 +/- 0.11 weighted mean of 7 clusters (Chavoyer 1999) (both for [Fe/H] = -1.5) Conclusions • Accurate CCD photometry of globular clusters and Fourier decomposition of the RR Lyrae stars light curves, lead to physical parameters of astrophysical relevance, and to general trends of these key physical parameters. These trends offer insight to the origin of the Oosterhoff groups and the structure of the Horiozontal Branch. • This technique offers an independent approach to the determination of the zero point in the RR Lyrae distance scale. • It provides the opportunity to discover and parametrize the Blazhko effect in RR Lyrae stars. • New image subtraction techniques allow finding new variables, even in very crowded fields like globular clusters core regions. OngoingOngoing workwork Presently our team has data, mostly taken in Hanle by Prof. Sunetra Giridhar, on the globular clusters: NGC 5466 [Fe/H] = -2.22: (19): masters thesis of Victoria Rojas, Mexico NGC 1904 [Fe/H] = -1.57: (3): under analysis during my visit to the IIA NGC 2419 [Fe/H] = -2.12: (35): under analysis during my visit to the IIA NGC 5053 [Fe/H] = -2.29: (9): to be reduced NGC 6981 [Fe/H] = -1.40: (28): to be reduced NGC 7492 [Fe/H] = -1.51: (3): to be reduced.
Load more

Recommended publications
  • Globular Clusters by Steve Gottlieb
    Southern Globulars 6/27/04 9:19 PM Nebula Filters by Andover Ngc 60 Telestar NCG-60 $148 Meade NGC60 For viewing emission and Find, compare and buy 60mm Computer Guided Refractor Telescope $181 planetary nebulae. Telescopes! Simply Fast Telescope! Includes 4 eye Free Shipping. Affiliate. Narrowband and O-III types Savings www.amazon.com pieces - Affiliate www.andcorp.com www.Shopping.com www.walmart.com Observing Down Under: Part I - Globular Clusters by Steve Gottlieb Omega Centauri - HST This is the first part in a series based on my trip to Australia last summer, covering observations of a few southern showpiece objects. The other parts in the series are: Southern Planetaries Southern Galaxies Two Southern Galaxy Groups These observing notes were made in early July while my family was staying at the Magellan Observatory (astronomical farmstead) for eight nights. The observatory is in the southern tablelands of New South Wales between Goulburn and Canberra (roughly 3.5 hrs from Sydney) and is hosted by Zane Hammond and his wife Fiona. Viewing the showpiece southern globulars was high on my observing priorities for Australia. Because the center of the Milky Way wheels overhead from -35° latitude, the globular system is much better placed and several of the best globulars in the sky which are completely inaccessible from the north are well placed. In the August issue of S&T, Les Dalrymple (who I observed with one evening), ranked M13 no better than 8th among the best globulars visible from Australia. I'd still jack up its ranking a couple of notches, but it's just one of the weak runnerups to 47 Tucana and Omega Centauri viewed over 75° up in the sky and behind NGC 6752, 6397 and M22.
    [Show full text]
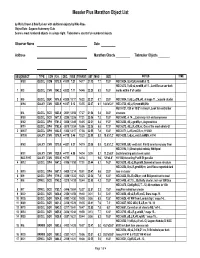
  • Messier Plus Marathon Text
    Messier Plus Marathon Object List by Wally Brown & Bob Buckner with additional objects by Mike Roos Object Data - Saguaro Astronomy Club Score is most numbered objects in a single night. Tiebreaker is count of un-numbered objects Observer Name Date Address Marathon Obects __________ Tiebreaker Objects ________ SEQ OBJECT TYPE CON R.A. DEC. RISE TRANSIT SET MAG SIZE NOTES TIME M 53 GLOCL COM 1312.9 +1810 7:21 14:17 21:12 7.7 13.0' NGC 5024, !B,vC,iR,vvmbM,st 12.. NGC 5272, !!,eB,vL,vsmbM,st 11.., Lord Rosse-sev dark 1 M 3 GLOCL CVN 1342.2 +2822 7:11 14:46 22:20 6.3 18.0' marks within 5' of center 2 M 5 GLOCL SER 1518.5 +0205 10:17 16:22 22:27 5.7 23.0' NGC 5904, !!,vB,L,eCM,eRi, st mags 11...;superb cluster M 94 GALXY CVN 1250.9 +4107 5:12 13:55 22:37 8.1 14.4'x12.1' NGC 4736, vB,L,iR,vsvmbM,BN,r NGC 6121, Cl,8 or 10 B* in line,rrr, Look for central bar M 4 GLOCL SCO 1623.6 -2631 12:56 17:27 21:58 5.4 36.0' structure M 80 GLOCL SCO 1617.0 -2258 12:36 17:21 22:06 7.3 10.0' NGC 6093, st 14..., Extremely rich and compressed M 62 GLOCL OPH 1701.2 -3006 13:49 18:05 22:21 6.4 15.0' NGC 6266, vB,L,gmbM,rrr, Asymmetrical M 19 GLOCL OPH 1702.6 -2615 13:34 18:06 22:38 6.8 17.0' NGC 6273, vB,L,R,vCM,rrr, One of the most oblate GC 3 M 107 GLOCL OPH 1632.5 -1303 12:17 17:36 22:55 7.8 13.0' NGC 6171, L,vRi,vmC,R,rrr, H VI 40 M 106 GALXY CVN 1218.9 +4718 3:46 13:23 22:59 8.3 18.6'x7.2' NGC 4258, !,vB,vL,vmE0,sbMBN, H V 43 M 63 GALXY CVN 1315.8 +4201 5:31 14:19 23:08 8.5 12.6'x7.2' NGC 5055, BN, vsvB stell.
    [Show full text]
  • Ghost Hunt Challenge 2020
    Virtual Ghost Hunt Challenge 10/21 /2020 (Sorry we can meet in person this year or give out awards but try doing this challenge on your own.) Participant’s Name _________________________ Categories for the competition: Manual Telescope Electronically Aided Telescope Binocular Astrophotography (best photo) (if you expect to compete in more than one category please fill-out a sheet for each) ** There are four objects on this list that may be beyond the reach of beginning astronomers or basic telescopes. Therefore, we have marked these objects with an * and provided alternate replacements for you just below the designated entry. We will use the primary objects to break a tie if that’s needed. Page 1 TAS Ghost Hunt Challenge - Page 2 Time # Designation Type Con. RA Dec. Mag. Size Common Name Observed Facing West – 7:30 8:30 p.m. 1 M17 EN Sgr 18h21’ -16˚11’ 6.0 40’x30’ Omega Nebula 2 M16 EN Ser 18h19’ -13˚47 6.0 17’ by 14’ Ghost Puppet Nebula 3 M10 GC Oph 16h58’ -04˚08’ 6.6 20’ 4 M12 GC Oph 16h48’ -01˚59’ 6.7 16’ 5 M51 Gal CVn 13h30’ 47h05’’ 8.0 13.8’x11.8’ Whirlpool Facing West - 8:30 – 9:00 p.m. 6 M101 GAL UMa 14h03’ 54˚15’ 7.9 24x22.9’ 7 NGC 6572 PN Oph 18h12’ 06˚51’ 7.3 16”x13” Emerald Eye 8 NGC 6426 GC Oph 17h46’ 03˚10’ 11.0 4.2’ 9 NGC 6633 OC Oph 18h28’ 06˚31’ 4.6 20’ Tweedledum 10 IC 4756 OC Ser 18h40’ 05˚28” 4.6 39’ Tweedledee 11 M26 OC Sct 18h46’ -09˚22’ 8.0 7.0’ 12 NGC 6712 GC Sct 18h54’ -08˚41’ 8.1 9.8’ 13 M13 GC Her 16h42’ 36˚25’ 5.8 20’ Great Hercules Cluster 14 NGC 6709 OC Aql 18h52’ 10˚21’ 6.7 14’ Flying Unicorn 15 M71 GC Sge 19h55’ 18˚50’ 8.2 7’ 16 M27 PN Vul 20h00’ 22˚43’ 7.3 8’x6’ Dumbbell Nebula 17 M56 GC Lyr 19h17’ 30˚13 8.3 9’ 18 M57 PN Lyr 18h54’ 33˚03’ 8.8 1.4’x1.1’ Ring Nebula 19 M92 GC Her 17h18’ 43˚07’ 6.44 14’ 20 M72 GC Aqr 20h54’ -12˚32’ 9.2 6’ Facing West - 9 – 10 p.m.
    [Show full text]
  • Astronomy 2008 Index
    Astronomy Magazine Article Title Index 10 rising stars of astronomy, 8:60–8:63 1.5 million galaxies revealed, 3:41–3:43 185 million years before the dinosaurs’ demise, did an asteroid nearly end life on Earth?, 4:34–4:39 A Aligned aurorae, 8:27 All about the Veil Nebula, 6:56–6:61 Amateur astronomy’s greatest generation, 8:68–8:71 Amateurs see fireballs from U.S. satellite kill, 7:24 Another Earth, 6:13 Another super-Earth discovered, 9:21 Antares gang, The, 7:18 Antimatter traced, 5:23 Are big-planet systems uncommon?, 10:23 Are super-sized Earths the new frontier?, 11:26–11:31 Are these space rocks from Mercury?, 11:32–11:37 Are we done yet?, 4:14 Are we looking for life in the right places?, 7:28–7:33 Ask the aliens, 3:12 Asteroid sleuths find the dino killer, 1:20 Astro-humiliation, 10:14 Astroimaging over ancient Greece, 12:64–12:69 Astronaut rescue rocket revs up, 11:22 Astronomers spy a giant particle accelerator in the sky, 5:21 Astronomers unearth a star’s death secrets, 10:18 Astronomers witness alien star flip-out, 6:27 Astronomy magazine’s first 35 years, 8:supplement Astronomy’s guide to Go-to telescopes, 10:supplement Auroral storm trigger confirmed, 11:18 B Backstage at Astronomy, 8:76–8:82 Basking in the Sun, 5:16 Biggest planet’s 5 deepest mysteries, The, 1:38–1:43 Binary pulsar test affirms relativity, 10:21 Binocular Telescope snaps first image, 6:21 Black hole sets a record, 2:20 Black holes wind up galaxy arms, 9:19 Brightest starburst galaxy discovered, 12:23 C Calling all space probes, 10:64–10:65 Calling on Cassiopeia, 11:76 Canada to launch new asteroid hunter, 11:19 Canada’s handy robot, 1:24 Cannibal next door, The, 3:38 Capture images of our local star, 4:66–4:67 Cassini confirms Titan lakes, 12:27 Cassini scopes Saturn’s two-toned moon, 1:25 Cassini “tastes” Enceladus’ plumes, 7:26 Cepheus’ fall delights, 10:85 Choose the dome that’s right for you, 5:70–5:71 Clearing the air about seeing vs.
    [Show full text]
  • Global Fitting of Globular Cluster Age Indicators
    A&A 456, 1085–1096 (2006) Astronomy DOI: 10.1051/0004-6361:20065133 & c ESO 2006 Astrophysics Global fitting of globular cluster age indicators F. Meissner1 and A. Weiss1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany e-mail: [meissner;weiss]@mpa-garching.mpg.de Received 3 March 2006 / Accepted 12 June 2006 ABSTRACT Context. Stellar models and the methods for the age determinations of globular clusters are still in need of improvement. Aims. We attempt to obtain a more objective method of age determination based on cluster diagrams, avoiding the introduction of biases due to the preference of one single age indicator. Methods. We compute new stellar evolutionary tracks and derive the dependence of age indicating points along the tracks and isochrone – such as the turn-off or bump location – as a function of age and metallicity. The same critical points are identified in the colour-magnitude diagrams of globular clusters from a homogeneous database. Several age indicators are then fitted simultaneously, and the overall best-fitting isochrone is selected to determine the cluster age. We also determine the goodness-of-fit for different sets of indicators to estimate the confidence level of our results. Results. We find that our isochrones provide no acceptable fit for all age indicators. In particular, the location of the bump and the brightness of the tip of the red giant branch are problematic. On the other hand, the turn-off region is very well reproduced, and restricting the method to indicators depending on it results in trustworthy ages. Using an alternative set of isochrones improves the situation, but neither leads to an acceptable global fit.
    [Show full text]
  • Distances and Ages of NGC 6397, NGC 6752 and 47 Tuc?
    A&A 408, 529–543 (2003) Astronomy DOI: 10.1051/0004-6361:20031003 & c ESO 2003 Astrophysics Distances and ages of NGC 6397, NGC 6752 and 47 Tuc? R. G. Gratton1, A. Bragaglia2, E. Carretta1, G. Clementini2,S.Desidera1, F. Grundahl3, and S. Lucatello1;4 1 INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy 2 INAF-Osservatorio Astronomico di Bologna, Via Ranzani 1, 40127 Bologna, Italy 3 Institute of Physics and Astronomy, Aarhus University, Ny Munkegade, 8000 Aarhus C, Denmark 4 Dipartimento di Astronomia, Universit`a di Padova, Italy, Vicolo dell’Osservatorio 2, 35122 Padova, Italy Received 28 April 2003 / Accepted 23 June 2003 Abstract. New improved distances and absolute ages for the Galactic globular clusters NGC 6397, NGC 6752, and 47 Tuc are obtained using the Main Sequence Fitting Method. We derived accurate estimates of reddening and metal abundance for these three clusters using a strictly differential procedure, where the Johnson B V and Str¨omgren b y colours and UVES high resolution spectra of turn-off stars and early subgiants belonging to the clusters− were compared to− similar data for field subdwarfs with accurate parallaxes measured by Hipparcos. The use of a reddening free temperature indicator (the profile of Hα) allowed us to reduce the error bars in reddening determinations to about 0.005 mag, and in metal abundances to 0.04 dex, in the scales defined by the local subdwarfs. Error bars in distances are then reduced to about 0.07 mag for each cluster, yielding ages with typical random errors of about 1 Gyr.
    [Show full text]
  • Introduction No. 104 July 2020
    No. 104 July 2020 Introduction I hope you are in good health as July’s Binocular Sky Newsletter reaches you. Although it is primarily targeted at binocular (and small telescope) observers in the UK, this particular community extends well south of the Equator. So welcome! Astronomical darkness, albeit short, return for locations south of about 53.5°N this month and, as binocular observers with our combination of maximum portability and minimal set-up time, we are well suited to take advantage of what this darkness reveals. I hesitate to write this, given recent history of our dashed expectations of “promising” comets, but we have another one, C/2020 F3 (NEOWISE). It’s visible in SOHO images and might just live up to expectations. (But it might not!) The binocular planets, Uranus and Neptune are becoming visible in the pre-dawn sky, as is Ceres but the short darkness means that there is only one suitable lunar occultations of a star, a dark-limb reappearance. If you would like to receive the newsletter automatically each month, please complete and submit the subscription form. You can get “between the newsletters” alerts, etc. via and . Binocular Sky Newsletter – July 2020 The Deep Sky (Hyperlinks will take you to finder charts and more information on the objects.) The all-sky chart on the next page reveals a lot about the structure of the Milky Way galaxy. Running in a strip down the middle, coinciding with the Milky Way itself, is the orange band of open clusters. Here, we are looking along the plane of the spiral arms which, of course, is where the star-forming (and, hence, open cluster forming) regions are.
    [Show full text]
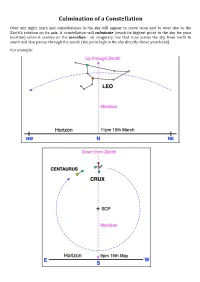
  • Culmination of a Constellation
    Culmination of a Constellation Over any night, stars and constellations in the sky will appear to move from east to west due to the Earth’s rotation on its axis. A constellation will culminate (reach its highest point in the sky for your location) when it centres on the meridian - an imaginary line that runs across the sky from north to south and also passes through the zenith (the point high in the sky directly above your head). For example: When to Observe Constellations The taBle shows the approximate time (AEST) constellations will culminate around the middle (15th day) of each month. Constellations will culminate 2 hours earlier for each successive month. Note: add an hour to the given time when daylight saving time is in effect. The time “12” is midnight. Sunrise/sunset times are rounded off to the nearest half an hour. Sun- Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Rise 5am 5:30 6am 6am 7am 7am 7am 6:30 6am 5am 4:30 4:30 Set 7pm 6:30 6pm 5:30 5pm 5pm 5pm 5:30 6pm 6pm 6:30 7pm And 5am 3am 1am 11pm 9pm Aqr 5am 3am 1am 11pm 9pm Aql 4am 2am 12 10pm 8pm Ara 4am 2am 12 10pm 8pm Ari 5am 3am 1am 11pm 9pm Aur 10pm 8pm 4am 2am 12 Boo 3am 1am 11pm 9pm 7pm Cnc 1am 11pm 9pm 7pm 3am CVn 3am 1am 11pm 9pm 7pm CMa 11pm 9pm 7pm 3am 1am Cap 5am 3am 1am 11pm 9pm 7pm Car 2am 12 10pm 8pm 6pm Cen 4am 2am 12 10pm 8pm 6pm Cet 4am 2am 12 10pm 8pm Cha 3am 1am 11pm 9pm 7pm Col 10pm 8pm 4am 2am 12 Com 3am 1am 11pm 9pm 7pm CrA 3am 1am 11pm 9pm 7pm CrB 4am 2am 12 10pm 8pm Crv 3am 1am 11pm 9pm 7pm Cru 3am 1am 11pm 9pm 7pm Cyg 5am 3am 1am 11pm 9pm 7pm Del
    [Show full text]
  • Caldwell Catalogue - Wikipedia, the Free Encyclopedia
    Caldwell catalogue - Wikipedia, the free encyclopedia Log in / create account Article Discussion Read Edit View history Caldwell catalogue From Wikipedia, the free encyclopedia Main page Contents The Caldwell Catalogue is an astronomical catalog of 109 bright star clusters, nebulae, and galaxies for observation by amateur astronomers. The list was compiled Featured content by Sir Patrick Caldwell-Moore, better known as Patrick Moore, as a complement to the Messier Catalogue. Current events The Messier Catalogue is used frequently by amateur astronomers as a list of interesting deep-sky objects for observations, but Moore noted that the list did not include Random article many of the sky's brightest deep-sky objects, including the Hyades, the Double Cluster (NGC 869 and NGC 884), and NGC 253. Moreover, Moore observed that the Donate to Wikipedia Messier Catalogue, which was compiled based on observations in the Northern Hemisphere, excluded bright deep-sky objects visible in the Southern Hemisphere such [1][2] Interaction as Omega Centauri, Centaurus A, the Jewel Box, and 47 Tucanae. He quickly compiled a list of 109 objects (to match the number of objects in the Messier [3] Help Catalogue) and published it in Sky & Telescope in December 1995. About Wikipedia Since its publication, the catalogue has grown in popularity and usage within the amateur astronomical community. Small compilation errors in the original 1995 version Community portal of the list have since been corrected. Unusually, Moore used one of his surnames to name the list, and the catalogue adopts "C" numbers to rename objects with more Recent changes common designations.[4] Contact Wikipedia As stated above, the list was compiled from objects already identified by professional astronomers and commonly observed by amateur astronomers.
    [Show full text]
  • A. L. Observing Programs Object Duplications
    A. L. OBSERVING PROGRAMS OBJECT DUPLICATIONS Compiled by Bill Warren Note: This report is limited to the following A. L. observing programs: Arp Peculiar Galaxies; Binocular Messier; Caldwell; Deep Sky Binocular; Galaxy Groups & Clusters; Globular Cluster; Herschel 400; Herschel II; Lunar; Messier; Open Cluster; Planetary Nebula; Universe Sampler; and Urban. It does not include the other A. L. observing programs, none of which contain duplicated objects. Like the A. L. itself, I’m using constellation names, not genitives (e.g., Orion, not Orionis) with double stars as an aid for beginners who might be referencing this. -Bill Warren Considerable duplication exists among the various A.L. observing programs. In fact, no less than 228 objects (8 lunar, 14 double stars and 206 deep-sky) appear in more than one program. For example, M42 is on the lists of the Messier, Binocular Messier, Universe Sampler and Urban Program. Duplication is important because, with certain exceptions noted below, if you observe an object once you can use that same observation in other A. L. programs in which that object appears. Of the 110 Messiers, 102 of them are also on the Binocular Messier list (18x50 version). To qualify for a Binocular Messier pin, you need only to find any 70 of them. Of course, they are duplicates only when you observe them in binocs; otherwise, they must be observed separately. Among its 100 targets, the Urban Program contains 41 Messiers, 14 Double Stars and 27 other deep-sky objects that appear on other lists. However, they are duplicates only if they are observed under light-polluted conditions; otherwise, they must be observed separately.
    [Show full text]
  • Cycle 9 Approved Programs
    Cycle 9 Approved Programs TYPE OF SCIENCE FIRST NAME LAST NAME INSTITUTION COUNTRY TITLE PROPOSAL CATEGORY A Morphological and Multicolor HST Survey for Ultrafaint Quasars, Sampling A Scott Anderson AR University of Washington United States AGN Broad Redshift Range Antonio Aparicio GO Instituto de Astrofi sica de Canarias Spain GAL Phoenix: "halo/disk" structures in dwarf galaxies John Bahcall GO Institute for Advanced Study United States HS Observing the next nearby supernova Ultraviolet Spectroscopy of Hot Horizontal-Branch Stars in the Globular Cluster Bradford Behr GO California Institute of Technology United States HS M13 David Bennett GO University of Notre Dame United States SP Confirmation of Black Hole, Planetary, and Binary Microlensing Events Klaus P. Beuermann GO Universitaets-Sternwarte Goettingen Germany HS FGS parallaxes of magnetic CVs Luciana Bianchi GO The Johns Hopkins University United States SP The Massive Star Content of NGC 6822 Torsten Boeker SNAP Space Telescope Science Institute United States GAL A Census of Nuclear Star Clusters in Late-Type Spiral Galaxies Ann Boesgaard GO Institute for Astronomy, University of Hawaii United States CS The Nucleosynthesis of Boron - Benchmarks for the Galactic Disk Howard Bond GO Space Telescope Science Institute United States CS WFPC2 Observations of Astrophysically Important Visual Binaries Howard Bond GO Space Telescope Science Institute United States HS Sakurai's Novalike Object: Real-Time Monitoring of a Stellar Thermal Pulse Amanda Bosh AR Lowell Observatory United States
    [Show full text]
  • SIAC Newsletter October 2013
    SOUTHEASTERN IOWA ASTRONOMY CLUB THE SIDEREAL TIMES OCTOBER 2013 A M EMBER SOCIETY OF THE ASTRONOMICAL LEAGUE CLUB OFFICERS : MINUTES SEPTEMBER 20, 2013 President Jim Hilkin called the meeting to is meeting night. Jim Hilkin gave an up- Executive Committee order with the following members in attend- date on the following maintenance President Jim Hilkin items: some additional dirt was added to Vice President Libby Snipes ance: Judy Smithson, Libby Snipes, Jim Treasurer Vicki Philabaum Wilt, Ray Reineke, Duane Gerling, Claus the east end of the berm to help block Secretary David Philabaum Benninghoven, Dave Philabaum, John Ton- headlights from cars coming from the Chief Observer David Philabaum ey, and Paul Sly. Vicki Philabaum conduct- beach and area E; the viburnum bushes Members-at-Large Claus Benninghoven ed a tour of the facility for a group from on the north side of the classroom were Duane Gerling Great River Christian School during the removed as they were getting too big for Blake Stumpf meeting. Libby moved to approve the the space; Jim has installed cabinet Board of Directors minutes as published, seconded by Jim Wilt, doors and created a storage area in the Chair Judy Hilkin motion passed. Jim Hilkin read the Treasur- Stone-Kelly dome; the new doors for Vice Chair Ray Reineke er's report from Vicki. Checks were written the Prugh-Carver Observatory are in, Secretary David Philabaum for the phone bill and to Ray for the new but there has been no word from SCC Members-at-Large David Martin about painting them so Barngrover's will Blake Stumpf motor for the Fecker telescope.
    [Show full text]