31151027790710.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CHAPTER 6 PICTORIAL SKETCHING 6-1Four Types of Projections
CHAPTER 6 PICTORIAL SKETCHING 6-1Four Types of Projections Types of Projections 6-2 Axonometric Projection As shown in figure below, axonometric projections are classified as isometric projection (all axes equally foreshortened), dimetric projection (two axes equally shortened), and trimetric projection (all three axes foreshortened differently, requiring different scales for each axis). (cont) Figures below show the contrast between an isometric sketch (i.e., drawing) and an isometric projection. The isometric projection is about 25% larger than the isometric projection, but the pictorial value is obviously the same. When you create isometric sketches, you do not always have to make accurate measurements locating each point in the sketch exactly. Instead, keep your sketch in proportion. Isometric pictorials are great for showing piping layouts and structural designs. Step by Step 6.1. Isometric Sketching 6-4 Normal and Inclined Surfaces in Isometric View Making an isometric sketch of an object having normal surfaces is shown in figure below. Notice that all measurements are made parallel to the main edges of the enclosing box – that is, parallel to the isometric axes. (cont) Making an isometric sketch of an object that has inclined surfaces (and oblique edges) is shown below. Notice that inclined surfaces are located by offset, or coordinate measurements along the isometric lines. For example, distances E and F are used to locate the inclined surface M, and distances A and B are used to locate surface N. 6-5 Oblique Surfaces in Isometric View Oblique surfaces in isometric view may be drawn by finding the intersections of the oblique surfaces with isometric planes. -

Technical Drawing School of Art, Design and Architecture Sarah Adeel | Nust – Spring 2011 the Ability to ’Document Imagination’
technical drawing school of art, design and architecture sarah adeel | nust – spring 2011 the ability to ’document imagination’. a mean to design reasoning spring 2011 perspective drawings technical drawing - perspective What is perspective drawing? Perspective originally comes from Latin word per meaning “through” and specere which means “to look.” These are combined to mean “to look through” or “to look at.” Intro to technical drawing perspective technical drawing - perspective What is perspective drawing? The “art definition” of perspective specifically describes creating the appearance of distance into our art. With time, the most typical “art definition” of perspective has evolved into “the technique of representing a three-dimensional image on a two-dimensional Intro to technical drawing surface.” perspective technical drawing - perspective What is perspective drawing? Perspective is about establishing “an eye” in art through which the audience sees. By introducing a sense of depth, space and an extension of reality into art is created, enhancing audience’s participation with it. When things appear more real, they become real to the senses. Intro to technical drawing perspective technical drawing - perspective What are the ingredients of perspective drawing? Any form consists of only three basic things: • it has size or amount • it covers distance • it extends in different directions Intro to technical drawing perspective technical drawing - perspective Everyday examples of perspective drawing Photography is an example of perspectives. In photos scenes are captured having depth, height and distance. Intro to technical drawing perspective technical drawing - perspective What is linear perspective drawing? Linear Perspective: Based on the way the human eye sees the world. -

Orthographic and Perspective Projection—Part 1 Drawing As
I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S From 3D to 2D: Orthographic and Perspective Projection—Part 1 •History • Geometrical Constructions 3D Viewing I • Types of Projection • Projection in Computer Graphics Andries van Dam September 15, 2005 3D Viewing I Andries van Dam September 15, 2005 3D Viewing I 1/38 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Drawing as Projection Early Examples of Projection • Plan view (orthographic projection) from Mesopotamia, 2150 BC: earliest known technical • Painting based on mythical tale as told by Pliny the drawing in existence Elder: Corinthian man traces shadow of departing lover Carlbom Fig. 1-1 • Greek vases from late 6th century BC show perspective(!) detail from The Invention of Drawing, 1830: Karl Friedrich • Roman architect Vitruvius published specifications of plan / elevation drawings, perspective. Illustrations Schinkle (Mitchell p.1) for these writings have been lost Andries van Dam September 15, 2005 3D Viewing I 2/38 Andries van Dam September 15, 2005 3D Viewing I 3/38 1 I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S I N T R O D U C T I O N T O C O M P U T E R G R A P H I C S Most Striking Features of Linear Early Perspective Perspective • Ways of invoking three dimensional space: shading • || lines converge (in 1, 2, or 3 axes) to vanishing point suggests rounded, volumetric forms; converging lines suggest spatial depth -

Indirect Proof
95698_ch02_067-120.qxp 9/5/13 4:53 PM Page 76 76 CHAPTER 2 ■ PARALLEL LINES In Exercises 28 to 30, write a formal proof of each theorem. 34. Given: Triangle MNQ with M obtuse ∠MNQ 28. If two parallel lines are cut by a transversal, then the pairs Construct: NE Ќ MQ, with E of alternate exterior angles are congruent. on MQ. N Q 29. If two parallel lines are cut by a transversal, then the pairs 35. Given: Triangle MNQ with of exterior angles on the same side of the transversal are Exercises 34, 35 obtuse ∠MNQ supplementary. Construct: MR Ќ NQ 30. If a transversal is perpendicular to one of two parallel lines, (HINT: Extend NQ.) then it is also perpendicular to the other line. 36. Given: A line m and a point T not on m 31. Suppose that two lines are cut by a transversal in such a way that the pairs of corresponding angles are not congruent. T Can those two lines be parallel? 32. Given: Line ᐍ and point P P m not on ᐍ —! Suppose that you do the following: Construct: PQ Ќ ᐍ i) Construct a perpendicular line r from T to line m. ii) Construct a line s perpendicular to line r at point T. 33. Given: Triangle ABC with B three acute angles What is the relationship between lines s and m? Construct: BD Ќ AC, with D on AC. A C 2.2 Indirect Proof KEY CONCEPTS Conditional Contrapositive Indirect Proof Converse Law of Negative Inverse Inference Let P S Q represent the conditional statement “If P, then Q.” The following statements are related to this conditional statement (also called an implication). -

Cylindrical Anamorphic Images –A Digital Method of Generation
ANDRZEJ ZDZIARSKI, MARCIN JONAK* CYLINDRICAL ANAMORPHIC IMAGES –A DIGITAL METHOD OF GENERATION CYFROWA METODA GENEROWANIA ANAMORFICZNYCH OBRAZÓW WALCOWYCH Abstract The aim of this paper is to present a practical construction for some cylindrical anamorphic images. The method is based on the analytic properties of reflective anamorphic image construction – topics which have been discussed in previous papers. This time, the authors deal with the analytical analysis of a transformation that is applied in order to obtain an anamorphic image, and provide an innovative digital notation of the reflective transformation discussed. The analytical model described here allows us to generate a cylindrical anamorphic image of any object that is represented in the form of a set of parametric equations. Some example anamorphic images together with their counter-images reflected in the surface of a cylindrical mirror will be presented here. The method of construction described enables the development of any design project of an anamorphic image in the urban planning environment and within the interiors of public spaces. Keywords: transformation, anamorphic image, visualization of an anamorphic image, reflective cylinder Streszczenie Niniejszy artykuł przedstawia praktyczną metodę konstruowania obrazów anamorficznych w oparciu o własności analityczne dla anamorf refleksyjnych. Praca jest kontynuacją zagadnień związanych z okre- śleniem geometrycznych zasad powstawania obrazów anamorficznych na bazie obrazu rzeczywistego, na- tomiast prezentuje ona analityczne przekształcenie oraz innowacyjny cyfrowy zapis takich obrazów. Tak więc opracowany model analityczny pozwala generować obrazy anamorficzne dowolnych projektowanych obiektów zapisanych w formie równań parametrycznych. Przykładowe anamorfy zaprezentowano wraz z ich obrazami restytuowanymi za pomocą prototypowego zwierciadła walcowego. Powyższe rozwiązania dają możliwość precyzyjnego projektowania obrazów anamorficznych w zurbanizowanej przestrzeni miej- skiej oraz architektonicznych wnętrzach przestrzeni publicznej. -

From 3D to 2D: Orthographic and Perspective Projection—Part 1
INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS From 3D to 2D: Orthographic and Perspective Projection—Part 1 Drawing as Projection • A painting based on a mythical tale as told by Pliny the Elder: a Corinthian maiden traces the shadow of her departing lover. • History • Geometrical Constructions • Types of Projection • Projection in Computer Graphics detail from The Invention of Drawing, 1830: Karl Friedrich Schinkle (Mitchell p.1) Andries van Dam September 17, 1998 3D Viewing I 1/31 Andries van Dam September 17, 1998 3D Viewing I 2/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Early Examples of Projection Early Perspective • Plan from Mesopotamia, 2150BC is earliest • Ways of invoking three dimensional space: known technical drawing in existence. rounded, volumetric forms suggested by shading, spatial depth of room suggested by • Greek vases from late 6th century BC show converging lines. perspective(!) • Not systematic—lines do not converge to a • Vitruvius, a Roman architect published single “vanishing” point. specifications of plan and elevation drawings, and perspective. Illustrations for these writings have been lost. Giotto, Confirmation of the rule of Saint Francis, c.1325 (Kemp p.8) Carlbom Fig. 1-1 Andries van Dam September 17, 1998 3D Viewing I 3/31 Andries van Dam September 17, 1998 3D Viewing I 4/31 INTRODUCTION TO COMPUTER GRAPHICS INTRODUCTION TO COMPUTER GRAPHICS Setting for “Invention” of Brunelleschi Perspective Projection • Invented systematic method of determining perspective projections in early 1400’s. • The Renaissance: new emphasis on Evidence that he created demonstration importance of individual point of view and panels, with specific viewing constraints for interpretation of world, power of complete accuracy of reproduction. -

Icons of Mathematics an EXPLORATION of TWENTY KEY IMAGES Claudi Alsina and Roger B
AMS / MAA DOLCIANI MATHEMATICAL EXPOSITIONS VOL 45 Icons of Mathematics AN EXPLORATION OF TWENTY KEY IMAGES Claudi Alsina and Roger B. Nelsen i i “MABK018-FM” — 2011/5/16 — 19:53 — page i — #1 i i 10.1090/dol/045 Icons of Mathematics An Exploration of Twenty Key Images i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page ii — #2 i i c 2011 by The Mathematical Association of America (Incorporated) Library of Congress Catalog Card Number 2011923441 Print ISBN 978-0-88385-352-8 Electronic ISBN 978-0-88385-986-5 Printed in the United States of America Current Printing (last digit): 10987654321 i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page iii — #3 i i The Dolciani Mathematical Expositions NUMBER FORTY-FIVE Icons of Mathematics An Exploration of Twenty Key Images Claudi Alsina Universitat Politecnica` de Catalunya Roger B. Nelsen Lewis & Clark College Published and Distributed by The Mathematical Association of America i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page iv — #4 i i DOLCIANI MATHEMATICAL EXPOSITIONS Committee on Books Frank Farris, Chair Dolciani Mathematical Expositions Editorial Board Underwood Dudley, Editor Jeremy S. Case Rosalie A. Dance Tevian Dray Thomas M. Halverson Patricia B. Humphrey Michael J. McAsey Michael J. Mossinghoff Jonathan Rogness Thomas Q. Sibley i i i i i i “MABK018-FM” — 2011/5/16 — 19:53 — page v — #5 i i The DOLCIANI MATHEMATICAL EXPOSITIONS series of the Mathematical As- sociation of America was established through a generous gift to the Association from Mary P. -

The Baroque in Games: a Case Study of Remediation
San Jose State University SJSU ScholarWorks Master's Theses Master's Theses and Graduate Research Spring 2020 The Baroque in Games: A Case Study of Remediation Stephanie Elaine Thornton San Jose State University Follow this and additional works at: https://scholarworks.sjsu.edu/etd_theses Recommended Citation Thornton, Stephanie Elaine, "The Baroque in Games: A Case Study of Remediation" (2020). Master's Theses. 5113. DOI: https://doi.org/10.31979/etd.n9dx-r265 https://scholarworks.sjsu.edu/etd_theses/5113 This Thesis is brought to you for free and open access by the Master's Theses and Graduate Research at SJSU ScholarWorks. It has been accepted for inclusion in Master's Theses by an authorized administrator of SJSU ScholarWorks. For more information, please contact [email protected]. THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION A Thesis Presented to The Faculty of the Department of Art History and Visual Culture San José State University In Partial Fulfillment of the Requirements for the Degree Masters of Arts By Stephanie E. Thornton May 2020 © 2020 Stephanie E. Thornton ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION by Stephanie E. Thornton APPROVED FOR THE DEPARTMENT OF ART HISTORY AND VISUAL CULTURE SAN JOSÉ STATE UNIVERSITY May 2020 Dore Bowen, Ph.D. Department of Art History and Visual Culture Anthony Raynsford, Ph.D. Department of Art History and Visual Culture Anne Simonson, Ph.D. Emerita Professor, Department of Art History and Visual Culture Christy Junkerman, Ph. D. Emerita Professor, Department of Art History and Visual Culture ABSTRACT THE BAROQUE IN GAMES: A CASE STUDY OF REMEDIATION by Stephanie E. -
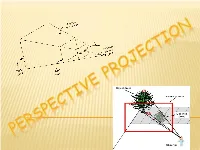
Perpective Presentation2.Pdf
Projections transform points in n-space to m-space, where m<n. Projection is 'formed' on the view plane (planar geometric projection) rays (projectors) projected from the center of projection pass through each point of the models and intersect projection plane. In 3-D, we map points from 3-space to the projection plane (PP) (image plane) along projectors (viewing rays) emanating from the center of projection (COP): TYPES OF PROJECTION There are two basic types of projections: Perspective – center of projection is located at a finite point in three space Parallel – center of projection is located at infinity, all the projectors are parallel Plane geometric projection Parallel Perspective Orthographic Axonometric Oblique Cavalier Cabinet Trimetric Dimetric Single-point Two-point Three-point Isometric PARALLEL PROJECTION • center of projection infinitely far from view plane • projectors will be parallel to each other • need to define the direction of projection (vector) • 3 sub-types Orthographic - direction of projection is normal to view plane Axonometric – constructed by manipulating object using rotations and translations Oblique - direction of projection not normal to view plane • better for drafting / CAD applications ORTHOGRAPHIC PROJECTIONS Orthographic projections are drawings where the projectors, the observer or station point remain parallel to each other and perpendicular to the plane of projection. Orthographic projections are further subdivided into axonom etric projections and multi-view projections. Effective in technical representation of objects AXONOMETRIC The observer is at infinity & the projectors are parallel to each other and perpendicular to the plane of projection. A key feature of axonometric projections is that the object is inclined toward the plane of projection showing all three surfaces in one view. -

Simple Andi Complete K-Points in Continuous and in Modular Projective Spaces
SIMPLE ANDI COMPLETE K-POINTS IN CONTINUOUS AND IN MODULAR PROJECTIVE SPACES by Beulah Armstrong Submitted to the Department of Mathematica and the faculty of the Graduate School of the University of Kansas in partial fulfillment.of I the requirements for the degree of Master of Arts. · Approved . 'UI/;~ _ Depar.tment of~ B I B L I ·o G R A P H Y. Allman, G.J. - Greek Geometry from Thales to Euclid - Longmans, Green & Co., London - 1889. Beman, W.W. and Smith, D.E. - Kls.in's Famous. Problems in ·Elementary Geometry - Ginn & Co., Boston - 1897. , , n Cantor, Moritz - Vorlesungen Uber Geschichte der Math- ematik - B.G. !l:eubner - Leipzig - 1894. Daviesf Iviathematical Dictionary and Cyclopedia of Math- ematical ~cieilce - A.s. Barnes & Co., New. York - 1855. Eisenlohr, Augu.st - Mathematisches Hendbuch der Alten Aegypter, Erst er Band - j. c. Hinrich, Le~pzig - 1877/ . _ Gow, James - A Short History of Greek Mathematics, University Press, Cambridge - 1884. Heath, T.L. - The i;chirteen Books of Euclid 1 s Elements, University Press; Cambridge - 1908. Lachlan, R. :.. Modern Pure Geometry - MacMillan & Co., New York - 1893. Tropfke, Johannes, Gesohichte der E1ementar Mathematik, Veit und Comp, Leipzig, 1903. Veblen and Young - Projective Geometry - Ginn & Co., New York - 1910. Young, J.W.A. - Monographs on Modern Mathematics, ·Longmans, Green & Co., New York - 1911. 1. INTRODUCTION. It is the pil:rpose of this paper, (1) ¥0 trace the development of the concepts of the simple· k-point ·and the complete k-point as they appear in mathematical literature and to £ormulate their definitions in a modular or an ordinary projective n-space (Se.ctioris 1 and 2); and (2) To determine the number of complete k-points in a modular projective plane (Section 3). -

Have You Ever Used Two Picture Planes to Draw a Single Perspective View?
G e n e r a l a r t i c l e have you ever used Two Picture Planes to Draw a Single Perspective View? T o m á S G arc í A S A l gad o Apparently, the use of two picture planes to draw a single view has be a more versatile plane that in addition to representing not been attempted before. Most perspective methods, after Alberti, the appearance of 3D objects would also serve to measure take for granted the use of a single picture plane, disregarding its likely real dimensions? Such a plane, in Modular Perspective [3], use in dual positions. What if two picture planes are necessary to ABSTRACT draw a single view—for example, given a lack of spatial references at can be called the perspective plane (PPL). On the PPL one can ground level to estimate the distance between two objects? This article measure and draw directly the three modular coordinates of demonstrates that to draw the interior of a building from which another all points of interest of any given object in space. In other building can be seen about 190 m away, where the projection of such words, the PPL is a true three-dimensional plane, despite building on the first picture plane would be imprecise, it may be wise to actually being two-dimensional. use a second picture plane. This leads to consideration of how objects In addition, the PPL can be of any size, since all points are change shape as they move away from the viewer. -

Polygrammal Symmetries in Bio-Macromolecules: Heptagonal Poly D(As4t) . Poly D(As4t) and Heptameric -Hemolysin
Polygrammal Symmetries in Bio-macromolecules: Heptagonal Poly d(As4T) . poly d(As4T) and Heptameric -Hemolysin A. Janner * Institute for Theoretical Physics, University of Nijmegen, Toernooiveld, 6525 ED Nijmegen The Netherlands Polygrammal symmetries, which are scale-rotation transformations of star polygons, are considered in the heptagonal case. It is shown how one can get a faithful integral 6-dimensional representation leading to a crystallographic approach for structural prop- erties of single molecules with a 7-fold point symmetry. Two bio-macromolecules have been selected in order to demonstrate how these general concepts can be applied: the left-handed Z-DNA form of the nucleic acid poly d(As4T) . poly d(As4T) which has the line group symmetry 7622, and the heptameric transmembrane pore protein ¡ -hemolysin. Their molecular forms are consistent with the crystallographic restrictions imposed on the combination of scaling transformations with 7-fold rotations. This all is presented in a 2-dimensional description which is natural because of the axial symmetry. 1. Introduction ture [4,6]. In a previous paper [1] a unifying general crystallography has The interest for the 7-fold case arose from the very nice axial been de®ned, characterized by the possibility of point groups of view of ¡ -hemolysin appearing in the cover picture of the book in®nite order. Crystallography then becomes applicable even to on Macromolecular Structures 1997 [7] which shows a nearly single molecules, allowing to give a crystallographic interpre- perfect 7-fold scale-rotation symmetry of the heptamer. In or- tation of structural relations which extend those commonly de- der to distinguish between law and accident, nucleic acids have noted as 'non-crystallographic' in protein crystallography.