Segmentation Meets Densest Subgraph Discovery
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Aluekartoitus HÄME C2 (05)
Aluekartoitus HÄME C2 (05) Lahti 9.11.2019 Pirkanmaa A Keltainen Pirkanmaa B Punainen 1 Aku Karvala Ilves 1 Henri Karppinen TAPPARA 30 Jimi Kuivila Ilves 30 Elmeri Pääsky TAPPARA 2 Vili Haapala Ilves 2 Akseli Kaartinen TAPPARA 3 Kalle Keinonen Ilves 3 Niko Korkola TAPPARA 4 Vili Majuri Ilves 4 Paavo Kulo HC Nokia 5 Kai Maunu Ilves 5 Tobias Nordlund TAPPARA 6 Nemo Pajula Ilves 6 Rasmus Ruusunen HC Nokia 7 Akusti Peltonen Ilves 7 Patrik Soikkeli TAPPARA 8 Topi Tikkanen Ilves 8 Viljami Vesto TAPPARA 9 Jirko Tukiainen Ilves 9 Jusa Vilppola HC Nokia 10 Tino Ilves Ilves 10 Joona Ala-Salmi HC Nokia 11 Emil Järventie Ilves 11 Joakim Almi TAPPARA 12 Kalle Kaipainen Ilves 12 Anton Dmitriev TAPPARA 13 Nooa Lamu Ilves 13 Konsta Frantsila HC Nokia 14 Juho Nyppeli Ilves 14 Sampo Heine TAPPARA 15 Leevi Pelkonen Ilves 15 Jesse Hietanen TAPPARA 16 Onni Puikkonen Ilves 16 Axel Koivula HC Nokia 17 Benjamin Rautiainen Ilves 17 Oskari Koppelojärvi TAPPARA 18 Jere Siiki Ilves 18 Dani Mikkonen TAPPARA 19 Otto Solin Ilves 19 Jonne Niemelä HC Nokia 20 Miko Uutela Ilves 20 Oiva Niininen TAPPARA 21 Eemil Virtanen Ilves 21 Timi Teuho-Markkola TAPPARA Päijät-Häme Sininen Kanta-Häme Valkoinen 1 Niklas Nikkilä Pelicans 1 Aaro Rintanen HPK 30 Jasper Lattu Pelicans 30 Topias Tuomisto VaPS 2 Jimi Junkkari Pelicans 2 Daniel Kemppainen HPK 3 Lauri Mattila Pelicans 3 Akseli Ketonen HPK 4 Riku Ylinen Pelicans 4 Eero Muhonen HPK 5 Henri Mattila Pelicans 5 Akseli Niskanen HPK 6 Jerry Hyvärinen Pelicans 26 Peetu Nurminen HPK 7 Miso Vihavainen Pelicans 7 Jimi Säteri HPK 8 Akseli -

Scheduling a Professional Sports League Using the PEAST Algorithm
Proceedings of the International MultiConference of Engineers and Computer Scientists 2014 Vol II, IMECS 2014, March 12 - 14, 2014, Hong Kong Scheduling a Professional Sports League using the PEAST Algorithm Kimmo Nurmi, Jari Kyngäs, Dries Goossens, Nico Kyngäs relaxed. If a team plays two home or two away games in Abstract— Generating a schedule for a professional sports two consecutive rounds, it is said to have a break. In league is an extremely demanding task. Good schedules have general, for reasons of fairness, breaks are to be avoided. many benefits for the league, such as higher incomes, lower However, a team can prefer to have two or more costs and more interesting and fairer seasons. This paper consecutive away games if its stadium is located far from presents the format played in the Finnish major ice hockey league in the 2013-2014 season. The format is very complicated the opponent’s venues, and the venues of these opponents requiring computational intelligence to generate an acceptable are close to each other. A series of consecutive away games schedule. We have used the PEAST algorithm to schedule the is called an away tour. league since the 2008-2009 season. We report our In a round robin tournament each team plays against each computational results especially for the 2013-2014 season. other team a fixed number of times. Most sports leagues play a double round robin tournament (2RR), where the Index Terms— sports scheduling; real-world scheduling; PEAST algorithm teams meet twice (once at home, once away), but quadruple round robin tournaments (4RR) are also quite common. -

Jääkiekon Liiga-Organisaatioiden Kannattavuus Ja Vakavaraisuus
Jääkiekon Liiga-organisaatioiden kannattavuus ja vakavaraisuus Laskentatoimi Maisterin tutkinnon tutkielma Olli Lähdesmäki 2014 Laskentatoimen laitos Aalto-yliopisto Kauppakorkeakoulu Powered by TCPDF (www.tcpdf.org) Aalto-yliopisto, PL 11000, 00076 AALTO www.aalto.fi Maisterintutkinnon tutkielman tiivistelmä Työn nimi Jääkiekon Liiga-organisaatioiden kannattavuus ja vakavaraisuus Tutkinto Kauppatieteiden maisteri Koulutusohjelma Laskentatoimi Työn ohjaaja Teemu Malmi Hyväksymisvuosi 2014 Sivumäärä 97 Kieli Suomi Tiivistelmä Tutkielman tavoitteena on tutkia jääkiekon Liiga-organisaatioiden kannattavuutta sekä vakavaraisuutta, niihin vaikuttavia tekijöitä sekä syitä niiden taustalla. Työssä on tarkasteltu urheilujohtamisen ja -liiketoiminnan lähtökohtia, kulmakiviä, sekä haasteita toimintaympäristössä. Tutkimuksessa on tarkasteltu Liiga-organisaatioiden taloudellista toimintaa aikavälillä 2000 - 2012 tilinpäätösanalyysien kautta. Analyysin tukena on toiminut Liiga-organisaatioiden johtohenkilöille tehdyt teemahaastattelut. Tutkielmassa kotimaisen jääkiekko-organisaation liiketoimintaa on verrattu pohjoisamerikkalaisten NHL:n organisaatioiden liiketoimintamalliin ja on analysoitu niiden keskeisimpiä eroja, pohjoisamerikkalaisten urheiluorganisaatioiden liiketoimintamallia on tarkasteltu kirjallisuuden pohjalta, sekä neljän NHL-organisaation johtotehtävissä olleelle Brian Burkelle tehdyllä teemahaastattelulla. Lisäksi on tarkasteltu Liigan ja sen organisaatioiden liiketoimintatason jalostamisen mahdollisuuksia ja suuntavaihtoehtoja, sekä -

0-2-0-0, T-7Th Atlantic Division
0-2-0-0, T-7th Atlantic Division NEED TO KNOW TODAY ● This is the fourth time in the last eight years Providence has started the season 0-2-0-0. The previous two times, the team went on to make the postseason. ● Cameron Hughes had his first career multipoint game Saturday vs Laval. ● Mark McNeill has scored goals in each of the team’s first two games of the season. ● Urho Vaakanainen, who was sent to Providence prior to their season opener, scored his first career point vs Hartford last Friday. ● After needing 47 games to score his first goal last season, Jeremy Lauzon scored a goal just two games into his sophomore campaign for the P-Bruins. ● Last season, McIntyre became the first P-Bruin ever to lead the AHL in shutouts (7). He is two shutouts away from tying Tim Thomas and Hannu Toivonen’s Providence record of 11 shutouts wearing the “Spoked P”. McIntyre is also six wins from tying John Grahame’s franchise record with 67 victories in net. ● If Szwarz has a 20-goal season, he will be the fifth player in team history with three 20+ goal seasons in a Providence uniform (Cameron Mann, Sergejs Zoltoks, Andy Hilbert and Craig Cunningham). TO VIEW THESE GAME NOTES ONLINE VISIT ProvidenceBruins.com/gamenotes SKATERS GOALTENDERS SPECIAL TEAMS SCORING BY PERIOD Goals McNeill (2) Games Vladar (2) PP% 12.5% Period 1 2 3 OT SO TOT Assists Hughes (2) Minutes Vladar (105:04) PK% 75% Points McNeill (3) GAA Vladar (1.71) PP Goals McNeill (1) 1 0 3 0 0 4 Rating Hughes/Lauzon (+1) SV% Vladar (92.9%) SH Goals Fyten (1) PRO PIM Fyten (7) Wins None -

Televisio SM-Liigassa – Historia Ja Nykypäivä
Santeri Seppälä Televisio SM-liigassa – historia ja nykypäivä Metropolia Ammattikorkeakoulu Medianomi AMK Elokuvan ja television koulutusohjelma Opinnäytetyö 2017 Tiivistelmä Tekijä(t) Santeri Seppälä Otsikko Media SM-liigassa – historia ja nykypäivä Sivumäärä 39 sivua Aika 5.5.2017 Tutkinto Medianomi AMK Koulutusohjelma Elokuvan ja television koulutusohjelma Suuntautumisvaihtoehto Televisio- ja radiotyö Ohjaaja(t) TV-työn lehtori Aura Neuvonen Tässä työssä tarkastellaan median, varsinkin television, roolia suomalaisen jääkiekkoilun pääsarjassa, Liigassa. Aihetta tutkitaan sekä televisiointihistorian että jääkiekkotoimittajien näkökulmasta selvittäen samalla suomalaisen jääkiekkoilun ja Liigan historian vaiheita. Työ on kolmiosainen. Ensimmäinen ja toinen luku käsittelevät suomalaisen jääkiekkoilun historiaa ja jääkiekon vaiheita Suomessa sekä Suomen jääkiekon pääsarjan Liigan tarinaa. Toinen osuus käsittelee median, etenkin television, suhdetta Liigaan. Tässä osuudessa selvitetään, mitkä asiat ovat johtaneet nykyiseen tilanteeseen eli mahdollisuuteen televisi- oida kauden jokainen ottelu suorana lähetyksenä. Osuudessa pureudutaan televisiointioi- keuksien lisäksi käytäntöihin ja katsojalukuihin. Kolmas osa perustuu Liigan parissa aiemmin tai nykyisin työskentelevien toimittajien haas- tatteluihin. Osuudessa pyritään selvittämään, mikä on median suhde Liigaan ja millainen rooli medialla on Suomen suosituimmassa palloilusarjassa. Opinnäytetyössä selviää, millainen on suomalaisen jääkiekkoilun historia ja millä tavalla media on historian -

COMPETITIVE BALANCE in VEIKKAUSLIIGA and LIIGA Roope
COMPETITIVE BALANCE IN VEIKKAUSLIIGA AND LIIGA Roope Töllikkö Master’s Thesis Sport and Exercise Promotion Faculty of Sport and Health Sciences University of Jyväskylä 2020 UNIVERSITY OF JYVÄSKYLÄ Faculty of Sport and Health Sciences TÖLLIKKÖ, ROOPE: Competitive balance in Veikkausliiga and Liiga ABSTRACT Master’s Thesis, 77 pages Social Sciences of Sport 2020 ----------------------------------------------------------------------------------------------------------------- Since the nominal paper by Simon Rottenberg in 1956, in which he discussed the notion of competitive balance for the first time, the theory has been a backbone in team sport economics. However, recent empirical evidence shows a clear trend of decrease in the levels of competitive balance across different leagues and sports around the world. A clear gap in the evidence exists in the Finnish sporting context and therefore this thesis aims to determine the current levels of competitive balance in Veikkausliiga and Liiga and how these levels have evolved throughout the last 30 years (1990-2019). The theoretical framework of this thesis can be traced to Simon Rottenberg’s theory of competitive balance and uncertainty of outcome, which is widely considered as the kick-start for team sport economics. The theory states that in order for a sport league to thrive, to attract spectators and thus be more profitable, the teams must be of approximately similar strength. Dominance, or in other words, a monopoly position of one or a few teams would harm the league, the main product itself. In order to measure the levels of competitive balance in the two leagues, a series of widely established measurement methods were used. The tools included the Herfindahl-Index, Gini Coefficient, standard deviation and historical winning percentages. -

Have Dynamic Capabilities Developed for Ostrobothnia's
Filip Sjöholm, c115610 Have Dynamic Capabilities Developed for Ostrobothnia’s Sports Teams during COVID-19? Master’s Thesis in Strategic Business Development VAASA 2021 1 CONTENTS LIST OF FIGURES AND TABLES 4 ABSTRACT 6 1. INTRODUCTION 8 1.1. Thesis structure 11 2. LITERATURE REVIEW 12 2.1. Stream 1: Dynamic Capabilities 12 2.1.1. History and Background of Dynamic Capabilities 12 2.1.2. Definitions of Dynamic Capabilities 15 2.1.3. Processes of Dynamic Capabilities 16 2.2. Stream 2: Sports Industry 27 2.2.1. Broadly about the topic (history, background) 29 2.2.2. Processes of the Sports Industry 31 2.2.3. Sports Management and Administration 35 2.2.4. Sports Industry in Finland 37 2.3. Synthesis and introduction of four-part framework 41 3. METHODOLOGY 44 3.1. Research strategy and method 44 3.2. Case selection Process 45 3.3. Data collection 46 3.4. Data analysis 47 2 3.5 Assessment of the quality of the data 48 4. FINDINGS 50 4.1. Within-Case Description and Analysis 50 4.1.1. Hockey-Team Vaasan Sport 50 4.1.2. FF Jaro 61 4.2. Cross-Case Analysis 71 4.2.1. Pattern 1, structuring lay-offs and re-negotiating contracts 72 4.2.2. Pattern 2, Digital advancements 73 4.2.3 Pattern 3, Psychological improvement 73 4.3. Synthesis 74 5. DISCUSSION 76 5.1. Theoretical implications 77 5.2. Managerial implications 78 5.3. Suggestions for future research 80 5.4. Limitations 82 REFERENCES 84 APPENDICES 89 Appendix1. -

Jotain Uutta, Paljon Perinteistä, Vähän Väriä
JOTAIN UUTTA, PALJON PERINTEISTÄ, VÄHÄN VÄRIÄ SOSIAALISEN MEDIAN HYÖDYNTÄMINEN JÄÄKIEKON SM-LIIGASSA JENNI JORMANAINEN | ESSI HILLGREN | JAAKKO HALTIA | HARRI JALONEN TURUN AMMATTIKORKEAKOULUN RAPORTTEJA 230 Turun ammattikorkeakoulu Turku 2016 Taitto: Etusivupaja ISBN 978-952-216-634-0 (painettu) ISSN 1457-7925 (painettu) Painopaikka: Suomen Yliopistopaino – Juvenes print Oy, Tampere 2016 ISBN 978-952-216-635-7 (pdf) ISSN 1459-7764 (elektroninen) Jakelu: loki.turkuamk.fi SISÄLLYS Johdanto ............................................................4 Tulokset pähkinänkuoressa .....................................5 Luokittelukriteeristö ................................................6 Sosiaalinen media haastaa liigajoukkueiden kommunikointikäytännöt ........................................7 Joukkuekohtaiset analyysit Blues .............................................................8 HIFK .............................................................9 HPK ............................................................10 Jenni Jormanainen, Essi Hillgren, Jaakko Haltia & Harri Jalonen Ilves ............................................................11 JYP .............................................................12 KalPa ..........................................................13 KooKoo .......................................................14 JOTAIN UUTTA, PALJON Kärpät .........................................................15 Lukko ..........................................................16 PERINTEISTÄ, VÄHÄN VÄRIÄ Pelicans .......................................................17 -
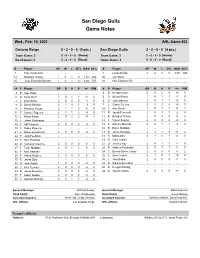
San Diego Gulls Game Notes
San Diego Gulls Game Notes Wed., Feb. 10, 2021 AHL Game #23 Ontario Reign 0 - 2 - 0 - 0 (0 pts.) San Diego Gulls 2 - 0 - 0 - 0 (4 pts.) Team Game: 3 0 - 0 - 0 - 0 (Home) Team Game: 3 2 - 0 - 0 - 0 (Home) Road Game: 3 0 - 2 - 0 - 0 (Road) Home Game: 3 0 - 0 - 0 - 0 (Road) # Player GP W L OTL GAA SV% # Player GP W L OTL GAA SV% 1 Troy Grosenick - - - - - - 1 Lukas Dostal 2 2 0 0 2.00 .945 31 Matthew Villata 1 0 1 0 4.04 .862 30 Jeff Glass - - - - - - 35 Jean-Francois Berube 1 0 1 0 6.04 .727 31 Olle Eriksson Ek - - - - - - # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 3 D Cole Hults - - - - - - 4 D Keegan Lowe 2 0 0 0 +2 0 6 D Sean Durzi 2 0 1 1 -4 4 5 D Simon Benoit 2 0 1 1 -1 0 7 C Brett Sutter 2 0 0 0 -1 0 6 D Josh Mahura 2 0 1 1 +2 0 8 D Daniel Brickley 2 1 0 1 -3 0 7 L Chase De Leo 2 2 2 4 +5 0 9 C Rasmus Kupari 2 1 1 2 0 0 10 C Alex Dostie 2 0 1 1 0 2 11 F Samuel Fagemo 2 1 1 2 -3 0 11 R Jacob Perreault 2 0 1 1 -2 0 12 L Blaine Byron 2 0 2 2 -4 4 12 R Brayden Tracey 2 0 0 0 0 0 13 L Johan Sodergran - - - - - - 13 C Trevor Zegras 2 2 3 5 +4 0 14 F Akil Thomas 2 0 0 0 -3 0 14 C Antoine Morand 2 0 1 1 -3 0 19 C Drake Rymsha - - - - - - 16 R Bryce Kindopp - - - - - - 21 L Mikey Eyssimont 2 0 0 0 -2 0 17 D Jamie Drysdale 2 1 1 2 +1 2 22 F Jack Poehling - - - - - - 18 R Matt Lorito 2 1 0 1 -2 0 23 F Nick Poehling - - - - - - 19 R Vinni Lettieri - - - - - - 24 D Cameron Gaunce 2 0 0 0 -2 2 21 D Jeremy Roy 2 0 1 1 +1 0 27 F Tyler Madden 2 0 1 1 0 0 22 R Andrew Poturalski 2 0 1 1 0 0 32 F Nick Halloran - - - - - - - 24 C Benoit-Olivier -

Katsaus SM- Liigaseurojen Taloudelliseen Tilanteeseen Kaudet 2018/2019 Ja 2019/2020 Sisällysluettelo
Katsaus SM- liigaseurojen taloudelliseen tilanteeseen Kaudet 2018/2019 ja 2019/2020 Sisällysluettelo 01 Alkusanat . 3 02 Yhteenveto . 4 03 Yhteisö. 7 Covid-19-pandemia ja SM-liiga . 8 SM-liiga Oy. 10 Naisten Liiga . 12 Liiketoiminta . 14 04 Analyysi liigasta . 16 Liikevaihto . 18 Liikevoitto . 26 Tulo- ja kulujakauma . 28 Oma pääoma ja Vakavaraisuus . 34 Henkilöstökulut . 39 05 Vaikutus. 49 Seurojen työllistävä vaikutus . 50 Yleisömäärät . 52 Brändi-analyysi . 56 Seurojen organisaatiokaavio . 58 06 Seurakohtaiset analyysit. 61 Keskiarvojoukkue . 62 Oy HIFK-Hockey Ab . 64 HPK Liiga Oy . 66 Ilves-Hockey Oy . 68 Jukurit HC Oy. 70 JYP Jyväskylä Oy . 72 KalPa Hockey Oy . 74 KooKoo Hockey Oy . 76 Oulun Kärpät Oy . 78 Rauman Lukko Oy . 80 Lahden Pelicans Oy . 82 Liiga-Saipa Oy . 84 Hockey-Team Vaasan Sport Oy . 86 Tamhockey Oy . 88 HC TPS Turku Oy . 90 HC Ässät Pori Oy . 92 07 Loppuanalyysi . .94 08 Liitteet . 98 Huomautukset . 100 2 Taklaukset| Katsaus SM-liigaseurojen jakeli. .taloudelliseen . tilanteeseen. Kaudet. .2018/2019 . .ja . 2019/2020 . .101 Alkusanat 01 Jääkiekko on Suomen seuratuin urheilulaji. Lätkän parissa Viime kaudella laatimassamme raportissa huomiota herättivät toimii satojatuhansia harrastajia, ammattilaisia sekä muita erityisesti pisteen hinta ja henkilöstökulut per piste. Nyt toimijoita. Jääkiekko-otteluita seuraa vuositasolla jäähalleissa nämä laskelmat ovat saaneet ketjukaverikseen yksittäisen ja kodeissa miljoonia katsojia. Jääkiekon yhteiskunnallinen katsojan arvon seuralle tulot per katsoja osiossa. Lisäksi vaikutus on Suomessa valtava. Siksi EY julkaisi myös tänä olemme tuoneet mukaan uusia tunnuslukuja, jotta sinä hyvä vuonna jääkiekon SM-liigajoukkueiden taloudellisia tietoja lukija pääset taklaamaan liigakiekkoilua uudelta kantilta. tarkastelevan raportin. Toivomme raportin tuovan esille Olemme tarkastelleet raportissa uusina aiheina seurojen mielenkiintoisia seikkoja niin SM-liigajoukkueille itselleen kuin työllistävää vaikutusta ja avanneet Naisten Liigan roolia kaikille liigaa seuraaville tahoillekin. -

Demand for Ice Hockey, the Factors Explaining Attendance of Ice Hockey Games in Finland
Demand for ice hockey, the factors explaining attendance of ice hockey games in Finland The study focuses on season 2007 – 2008 ice hockey league games in Finland. The aim is to explain factors affecting attendance. During the season there were 392 games played excluding playoff games. The total attendance number was 1964626. Both population of the home team and the visitor have a statistically significant effect on attendance as well as distance between home town and visitor’s town. Local games have a bigger attendance than other games. The demand is not elastic with respect to the ticket price. Success of both the home team and the visitor has an effect: home team’s success with a positive and visitor’s with a negative coefficient. The number of plays already played has a negative effect. Weekday effect is important: the attendance is bigger during Saturdays. Also the day temperature has an effect: the colder, the bigger attendance. That effect is small but still statistically significant. The unemployment rate has no effect, and the success factor of the last three games does not seem to explain as well as the success factor of all games played. Keywords: Ice hockey, Attendance, Finland, Temperature Demand for ice hockey, the factors explaining attendance of ice hockey games in Finland 1. Introduction This paper uses regular season 2007 – 2008 Finnish ice hockey attendance figures to examine the explaining determinants. Simple economic theory suggests that the demand for attendance should depend on the ticket price of the game and travel costs, the incomes of spectators, the prices of substitute goods and market size (Simmons 2006). -

Ilves Brandbook Media.Pdf
06/2020 BE MORE ILVES ILVES HOCKEY Opas Ilves Hockeyn henkilökunnalle sekä kaikille urheiluseuran sidosryhmille, joilla on jokin rooli Ilveksen graafisessa, BRAND BOOK tekstin tai sisällön tuotannossa. BE MORE ILV E S Brändikirjan sisältö 1 2 3 4 BRÄNDI LOGO JA VÄRIT FONTIT KUVAMAAILMA 1.0 Johdanto 5 2.0 Ilveksen logo 43 3.0 Typografia 53 4.0 Kuvien käyttö 59-63 1.1 Tarina 6 2.1 Logon käyttö 44-45 3.1 Brändi ja identiteetti 54 4.1 Identiteetin sovelluksia 64-67 1.2 Arvot 7 2.2 Yleisimmät virheet 46 3.2 Brändikirjasin 55 1.3 Missio 8 2.3 Tekstiä sisältävä logo 47 3.3 Sisältökirjasin 56 1.4 Be More Ilves 10-29 2.4 Tekstielementti 48-49 3.4 Numerot 57 1.5 Tone of Voice 30-41 2.5 Tunnusvärit 50 ILVES HOCKEY | Brändikirja 1 BRÄNDI Brändimme on se, mitä Ilveksestä puhutaan. 4 ILVES HOCKEY | Brändikirja 1.0 JOHDANTO TÄMÄ ON VIRALLINEN ILVES HOCKEYN BRAND BOOK Brändi ei ole vain tunnistettava logo, se on tarina, jonka takana voi ylpeästi seistä. Se puhuttelee, luo tuntemuksia ja kasvaa jatkuvasti ajan kanssa. Brändin arvo muodostuu nimen ja logon tunnettuudesta, asiakkaiden uskollisuudesta, laadun tunteesta, mielikuvista ja keskustelusta brändin ympärillä. On tärkeä ymmärtää, että jokainen Ilvesläinen on mukana rakentamassa tätä yhteistä tarinaa. Ja jotta tarinamme olisi vahva ja yhtenäinen, olemme luoneet ohjeeksi tämän Brand Bookin. Kun toistamme yhteistä viestiä ja yhtenäistä ilmettä eri tilanteissa ja eri kanavissa, tarinamme vahvistuu ja tarttuu myös seuraajiimme. Koska brändimme on lopulta se, mitä Ilveksestä puhutaan. Brand Book toimii Ilves Hockeyn ohjenuorana, josta saa apua ilmeen soveltamiseen eri materiaaleissa ja medioissa.