Bootstrapping Statistical Inference for Off-Policy Evaluation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
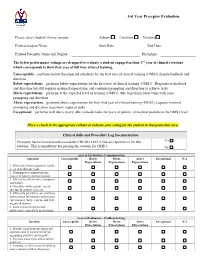
Third Year Preceptor Evaluation Form
3rd Year Preceptor Evaluation Please select student’s home campus: Auburn Carolinas Virginia Printed Student Name: Start Date: End Date: Printed Preceptor Name and Degree: Discipline: The below performance ratings are designed to evaluate a student engaged in their 3rd year of clinical rotations which corresponds to their first year of full time clinical training. Unacceptable – performs below the expected standards for the first year of clinical training (OMS3) despite feedback and direction Below expectations – performs below expectations for the first year of clinical training (OMS3). Responds to feedback and direction but still requires maximal supervision, and continual prompting and direction to achieve tasks Meets expectations – performs at the expected level of training (OMS3); able to perform basic tasks with some prompting and direction Above expectations – performs above expectations for their first year of clinical training (OMS3); requires minimal prompting and direction to perform required tasks Exceptional – performs well above peers; able to model tasks for peers or juniors, of medical students at the OMS3 level Place a check in the appropriate column to indicate your rating for the student in that particular area. Clinical skills and Procedure Log Documentation Preceptor has reviewed and discussed the CREDO LOG (Clinical Experience) for this Yes rotation. This is mandatory for passing the rotation for OMS 3. No Area of Evaluation - Communication Question Unacceptable Below Meets Above Exceptional N/A Expectations Expectations Expectations 1. Effectively listen to patients, family, peers, & healthcare team. 2. Demonstrates compassion and respect in patient communications. 3. Effectively collects chief complaint and history. 4. Considers whole patient: social, spiritual & cultural concerns. -

The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns
atmosphere Review The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns Susan Prichard 1,*, N. Sim Larkin 2, Roger Ottmar 2, Nancy H.F. French 3 , Kirk Baker 4, Tim Brown 5, Craig Clements 6 , Matt Dickinson 7, Andrew Hudak 8 , Adam Kochanski 9, Rod Linn 10, Yongqiang Liu 11, Brian Potter 2, William Mell 2 , Danielle Tanzer 3, Shawn Urbanski 12 and Adam Watts 5 1 University of Washington School of Environmental and Forest Sciences, Box 352100, Seattle, WA 98195-2100, USA 2 US Forest Service Pacific Northwest Research Station, Pacific Wildland Fire Sciences Laboratory, Suite 201, Seattle, WA 98103, USA; [email protected] (N.S.L.); [email protected] (R.O.); [email protected] (B.P.); [email protected] (W.M.) 3 Michigan Technological University, 3600 Green Court, Suite 100, Ann Arbor, MI 48105, USA; [email protected] (N.H.F.F.); [email protected] (D.T.) 4 US Environmental Protection Agency, 109 T.W. Alexander Drive, Durham, NC 27709, USA; [email protected] 5 Desert Research Institute, 2215 Raggio Parkway, Reno, NV 89512, USA; [email protected] (T.B.); [email protected] (A.W.) 6 San José State University Department of Meteorology and Climate Science, One Washington Square, San Jose, CA 95192-0104, USA; [email protected] 7 US Forest Service Northern Research Station, 359 Main Rd., Delaware, OH 43015, USA; [email protected] 8 US Forest Service Rocky Mountain Research Station Moscow Forestry Sciences Laboratory, 1221 S Main St., Moscow, ID 83843, USA; [email protected] 9 Department of Atmospheric Sciences, University of Utah, 135 S 1460 East, Salt Lake City, UT 84112-0110, USA; [email protected] 10 Los Alamos National Laboratory, P.O. -
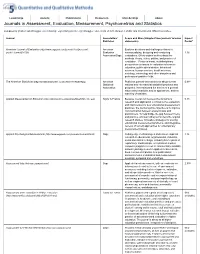
Journals in Assessment, Evaluation, Measurement, Psychometrics and Statistics
Leadership Awards Publications Resources Membership About Journals in Assessment, Evaluation, Measurement, Psychometrics and Statistics Compiled by (mailto:[email protected]) Lihshing Leigh Wang (mailto:[email protected]) , Chair of APA Division 5 Public and International Affairs Committee. Journal Association/ Scope and Aims (Adapted from journals' mission Impact Publisher statements) Factor* American Journal of Evaluation (http://www.sagepub.com/journalsProdDesc.nav? American Explores decisions and challenges related to prodId=Journal201729) Evaluation conceptualizing, designing and conducting 1.16 Association/Sage evaluations. Offers original articles about the methods, theory, ethics, politics, and practice of evaluation. Features broad, multidisciplinary perspectives on issues in evaluation relevant to education, public administration, behavioral sciences, human services, health sciences, sociology, criminology and other disciplines and professional practice fields. The American Statistician (http://amstat.tandfonline.com/loi/tas#.Vk-A2dKrRpg) American Publishes general-interest articles about current 0.98^ Statistical national and international statistical problems and Association programs, interesting and fun articles of a general nature about statistics and its applications, and the teaching of statistics. Applied Measurement in Education (http://www.tandf.co.uk/journals/titles/08957347.asp) Taylor & Francis Because interaction between the domains of 0.33 research and application is critical to the evaluation and improvement of -

Research Designs for Program Evaluations
03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 79 CHAPTER 3 RESEARCH DESIGNS FOR PROGRAM EVALUATIONS Introduction 81 What Is Research Design? 83 The Origins of Experimental Design 84 Why Pay Attention to Experimental Designs? 89 Using Experimental Designs to Evaluate Programs: The Elmira Nurse Home Visitation Program 91 The Elmira Nurse Home Visitation Program 92 Random Assignment Procedures 92 The Findings 93 Policy Implications of the Home Visitation Research Program 94 Establishing Validity in Research Designs 95 Defining and Working With the Four Kinds of Validity 96 Statistical Conclusions Validity 97 Working with Internal Validity 98 Threats to Internal Validity 98 Introducing Quasi-Experimental Designs: The Connecticut Crackdown on Speeding and the Neighborhood Watch Evaluation in York, Pennsylvania 100 79 03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 80 80–●–PROGRAM EVALUATION AND PERFORMANCE MEASUREMENT The Connecticut Crackdown on Speeding 101 The York Neighborhood Watch Program 104 Findings and Conclusions From the Neighborhood Watch Evaluation 105 Construct Validity 109 External Validity 112 Testing the Causal Linkages in Program Logic Models 114 Research Designs and Performance Measurement 118 Summary 120 Discussion Questions 122 References 125 03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 81 Research Designs for Program Evaluations–●–81 INTRODUCTION Over the last 30 years, the field of evaluation has become increasingly diverse in terms of what is viewed as proper methods and practice. During the 1960s and into the 1970s most evaluators would have agreed that a good program evaluation should emulate social science research and, more specifically, methods should come as close to randomized experiments as possible. -

An Outline of Critical Thinking
AN OUTLINE OF CRITICAL THINKING LEVELS OF INQUIRY 1. Information: correct understanding of basic information. 2. Understanding basic ideas: correct understanding of the basic meaning of key ideas. 3. Probing: deeper analysis into ideas, bases, support, implications, looking for complexity. 4. Critiquing: wrestling with tensions, contradictions, suspect support, problematic implications. This leads to further probing and then further critique, & it involves a recognition of the limitations of your own view. 5. Assessment: final evaluation, acknowledging the relative strengths & limitations of all sides. 6. Constructive: an articulation of your own view, recognizing its limits and areas for further inquiry. EMPHASES Issues! Reading: Know the issues an author is responding to. Writing: Animate and organize your paper around issues. Complexity! Reading: assume that there is more to an idea than is immediately obvious; assume that a key term can be used in various ways and clarify the meaning used in the article; assume that there are different possible interpretations of a text, various implications of ideals, and divergent tendencies within a single tradition, etc. Writing: Examine ideas, values, and traditions in their complexity: multiple aspects of the ideas, different possible interpretations of a text, various implications of ideals, different meanings of terms, divergent tendencies within a single tradition, etc. Support! Reading: Highlight the kind and degree of support: evidence, argument, authority Writing: Support your views with evidence, argument, and/or authority Basis! (ideas, definitions, categories, and assumptions) Reading: Highlight the key ideas, terms, categories, and assumptions on which the author is basing his views. Writing: Be aware of the ideas that give rise to your interpretation; be conscious of the definitions you are using for key terms; recognize the categories you are applying; critically examine your own assumptions. -

Project Quality Evaluation – an Essential Component of Project Success
Mathematics and Computers in Biology, Business and Acoustics Project Quality Evaluation – An Essential Component of Project Success DUICU SIMONA1, DUMITRASCU ADELA-ELIZA2, LEPADATESCU BADEA2 Descriptive Geometry and Technical Drawing Department1, Manufacturing Engineering Department2, Faculty of Manufacturing Engineering and Industrial Management “Transilvania” University of Braşov 500036 Eroilor Street, No. 29, Brasov ROMANIA [email protected]; [email protected]; [email protected]; Abstract: - In this article are presented aspects, elements and indices regarding project quality management as a potential source of sustainable competitive advantages. The success of a project depends on implementation of the project quality processes: quality planning, quality assurance, quality control and continuous process improvement drive total quality management success. Key-Words: - project management, project quality management, project quality improvement. 1 Introduction negative impact on the possibilities of planning and Project management is the art — because it requires the carrying out project activities); skills, tact and finesse to manage people, and science — • supply chain problems; because it demands an indepth knowledge of an • lack of resources (funds or trained personnel); assortment of technical tools, of managing relatively • organizational inefficiency. short-term efforts, having finite beginning and ending - external factors: points, usually with a specific budget, and with customer • natural factors (natural disasters); specified performance criteria. “Short term” in the • external economic influences (adverse change in context of project duration is dependent on the industry. currency exchange rate used in the project); The longer and more complex a project is, the more it • reaction of people affected by the project; will benefit from the application of project management • implementation of economic or social policy tools. -

Statistical Inference a Work in Progress
Ronald Christensen Department of Mathematics and Statistics University of New Mexico Copyright c 2019 Statistical Inference A Work in Progress Springer v Seymour and Wes. Preface “But to us, probability is the very guide of life.” Joseph Butler (1736). The Analogy of Religion, Natural and Revealed, to the Constitution and Course of Nature, Introduction. https://www.loc.gov/resource/dcmsiabooks. analogyofreligio00butl_1/?sp=41 Normally, I wouldn’t put anything this incomplete on the internet but I wanted to make parts of it available to my Advanced Inference Class, and once it is up, you have lost control. Seymour Geisser was a mentor to Wes Johnson and me. He was Wes’s Ph.D. advisor. Near the end of his life, Seymour was finishing his 2005 book Modes of Parametric Statistical Inference and needed some help. Seymour asked Wes and Wes asked me. I had quite a few ideas for the book but then I discovered that Sey- mour hated anyone changing his prose. That was the end of my direct involvement. The first idea for this book was to revisit Seymour’s. (So far, that seems only to occur in Chapter 1.) Thinking about what Seymour was doing was the inspiration for me to think about what I had to say about statistical inference. And much of what I have to say is inspired by Seymour’s work as well as the work of my other professors at Min- nesota, notably Christopher Bingham, R. Dennis Cook, Somesh Das Gupta, Mor- ris L. Eaton, Stephen E. Fienberg, Narish Jain, F. Kinley Larntz, Frank B. -

Deconstructing Public Administration Empiricism
Deconstructing Public Administration Empiricism A paper written for Anti-Essentialism in Public Administration a conference in Fort Lauderdale, Florida March 2 and 3, 2007 Larry S. Luton Graduate Program in Public Administration Eastern Washington University 668 N. Riverpoint Blvd., Suite A Spokane, WA 99202-1660 509/358-2247 voice 509/358-2267 fax [email protected] Deconstructing Public Administration Empiricism: Short Stories about Empirical Attempts to Study Significant Concepts and Measure Reality Larry S. Luton Eastern Washington University Like much social science empiricism, public administration empiricism at its best recognizes that it presents probabilistic truth claims rather than universalistic ones. In doing so, public administration empiricists are (to a degree) recognizing the tenuousness of their claim that their approach to research is better connected to reality than research that does not adhere to empiricist protocols. To say that one is 95% confident that an empirical model explains 25% of the variation being studied is not a very bold claim about understanding reality. They are also masking a more fundamental claim that they know an objective reality exists. The existence of an objective reality is the essential foundation upon which empiricism relies for its claim to provide a research approach that is superior to all others and, therefore, is in a position to set the standards to which all research should be held (King, Keohane, & Verba 1994; Brady & Collier, 2004). In one of the most direct expressions of this claim, Meier has stated “There is an objective reality” (Meier 2005, p. 664). In support of that claim, he referenced 28,000 infant deaths in the U.S. -

The Psychometric Evaluation of a Personality Selection Tool
Seattle aP cific nivU ersity Digital Commons @ SPU Industrial-Organizational Psychology Dissertations Psychology, Family, and Community, School of Spring January 18th, 2017 The syP chometric Evaluation of a Personality Selection Tool James R. Longabaugh Seattle Pacific nU iversity Follow this and additional works at: https://digitalcommons.spu.edu/iop_etd Part of the Industrial and Organizational Psychology Commons Recommended Citation Longabaugh, James R., "The sP ychometric Evaluation of a Personality Selection Tool" (2017). Industrial-Organizational Psychology Dissertations. 10. https://digitalcommons.spu.edu/iop_etd/10 This Dissertation is brought to you for free and open access by the Psychology, Family, and Community, School of at Digital Commons @ SPU. It has been accepted for inclusion in Industrial-Organizational Psychology Dissertations by an authorized administrator of Digital Commons @ SPU. The Psychometric Evaluation of a Personality Selection Tool James Longabaugh A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Industrial-Organizational Psychology Seattle Pacific University January, 2017 THE PSYCHOMETRIC EVALUATION OF A PERSONALITY INSTRUMENT i Acknowledgments The question of whether it is the journey or the destination that is more important has never been so clear; it is the journey. There have been so many people who have helped and supported me along the way, and I only hope that I can acknowledge as many of them as possible. It is with great gratitude that I extend thanks to each and every one who has helped me attain this high honor, but more so for their contributions of inspiration and motivation along the way. First and foremost, my advisor, my mentor, and my dissertation chair, Dr. -

Quality Management in Education
Quality Management in Education Self-evaluation for quality improvement Quality Management in Education Self-evaluation for quality improvement HM Inspectorate of Education 2006 © Crown copyright 2006 ISBN: 0 7053 1087 6 HM Inspectorate of Education Denholm House Almondvale Business Park Almondvale Way Livingston EH54 6GA Tel: 01506 600 200 Fax: 01506 600 337 E-mail: [email protected] Produced for HMIE by Astron B45597 04/06 Published by HMIE, April 2006 This material may be copied without further permission by education authorities and education institutions in Scotland for use in self-evaluation and planning. The report may be produced in part, except for commercial purposes, or in connection with a prospectus or advertisement, provided that the source and date therefore are stated. ii_iii Contents Foreword iv Acknowledgements vi Introduction 1 Part 1 Self-evaluation in the local authority context 3 Part 2 The framework for self-evaluation explained 7 Part 3 The six-point scale 14 Part 4 Performance and quality indicators 16 Part 5 Indicators, themes and illustrations 22 Part 6 Using performance and quality indicators for self-evaluation 77 Part 7 Self-evaluation questions and sources of evidence 86 Appendix I The relationships between Quality Management in Education 2 and other quality frameworks. 104 QUALITY MANAGEMENT IN EDUCATION 2 – SELF-EVALUATION FOR QUALITY IMPROVEMENT Foreword Quality Management in Education (QMIE), published by Her Majesty’s Inspectorate of Education (HMIE) in 2000, set out a framework for self-evaluation of the performance of education authorities in Scotland. It also provided the basis for the first cycle of external scrutiny by HMIE, namely the Inspection of the Education Functions of Local Authorities (INEA). -

1 Department of Sociology Florida Atlantic University Procedures and Criteria for Annual Evaluation the Department's Goal Is E
Department of Sociology Florida Atlantic University Procedures and Criteria for Annual Evaluation The Department’s goal is excellence in instruction, scholarship, and service to institution, discipline and community. To that end, we adopt this set of procedures and criteria for annual evaluation. The annual evaluation criteria provide members of the Department of Sociology with guidelines for how to proceed on an annual basis to achieve both departmental and disciplinary standards. We recognize that an annual evaluation is a limited cross-section of an academic career and that, therefore, promotion and tenure criteria necessarily address a broader set of issues. Faculty are urged to regularly review the department’s promotion and tenure criteria. Annual evaluations are an important part of promotion and tenure decision but are not all that is considered. Evaluation of Instruction The department recognized that instruction incorporates a broad range of activities along with teaching. Both quantitative and qualitative data will be used for evaluating faculty members’ instructional accomplishments and to assess overall performance in this area of the assignment. The three sections below outline the sets of activities the department will consider in the evaluation of instruction. The minimal data used to evaluate instruction: SPOT scores, syllabi, and grade distributions. A. The basic elements of instructional work are in assigned classes, and its quality is assessed through an evaluation of based: • Student assessment of instructional quality, indicated primarily through but not exclusively by SPOT scores o The department recognizes that no single item adequately captures student sentiment about an instructor and a course. This is clearly shown by the relatively low inter-item correlations. -

Principles of Statistical Inference
Principles of Statistical Inference In this important book, D. R. Cox develops the key concepts of the theory of statistical inference, in particular describing and comparing the main ideas and controversies over foundational issues that have rumbled on for more than 200 years. Continuing a 60-year career of contribution to statistical thought, Professor Cox is ideally placed to give the comprehensive, balanced account of the field that is now needed. The careful comparison of frequentist and Bayesian approaches to inference allows readers to form their own opinion of the advantages and disadvantages. Two appendices give a brief historical overview and the author’s more personal assessment of the merits of different ideas. The content ranges from the traditional to the contemporary. While specific applications are not treated, the book is strongly motivated by applications across the sciences and associated technologies. The underlying mathematics is kept as elementary as feasible, though some previous knowledge of statistics is assumed. This book is for every serious user or student of statistics – in particular, for anyone wanting to understand the uncertainty inherent in conclusions from statistical analyses. Principles of Statistical Inference D.R. COX Nuffield College, Oxford CAMBRIDGE UNIVERSITY PRESS Cambridge, New York, Melbourne, Madrid, Cape Town, Singapore, São Paulo Cambridge University Press The Edinburgh Building, Cambridge CB2 8RU, UK Published in the United States of America by Cambridge University Press, New York www.cambridge.org Information on this title: www.cambridge.org/9780521866736 © D. R. Cox 2006 This publication is in copyright. Subject to statutory exception and to the provision of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press.