DOCSLIB.ORG

Anthropometric Study of the Femur an Automated Approach

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Anthropometric Study of the Femur an Automated Approach Anthropometric Study of the Femur An Automated Approach Chi Bang Abe LAU July 2009 A Thesis Submitted For The Degree Of Doctor Of Philosophy Surgical & Orthopaedic Research Laboratories Copyright and DAI Statement ’I hereby grant the University of New South Wales or its agents the right to archive and to make available my thesis or dissertation in whole or part in the University libraries in all forms of media, now or here after known, subject to the provisions of the Copyright Act 1968. I retain all proprietary rights, such as patent rights. I also retain the right to use in future works (such as articles or books) all or part of this thesis or dissertation. I also authorise University Microfilms to use the 350 word abstract of my thesis in Dissertation Abstracts International (this is applicable to doctoral theses only). I have either used no substantial portions of copyright material in my thesis or I have obtained permission to use copyright material; where permission has not been granted I have applied/will apply for a partial restriction of the digital copy of my thesis or dissertation.’ Signed: Date: Authenticity Statement ’I certify that the Library deposit digital copy is a direct equivalent of the final officially approved version of my thesis. No emendation of content has occurred and if there are any minor variations in formatting, they are the result of the conversion to digital format.’ Signed: Date: Originality Statement ’I hereby declare that this submission is my own work and to the best of my knowledge it contains no materials previously published or written by another person, or substantial proportions of mate- rial which have been accepted for the award of any other degree or diploma at UNSW or any other educational institution, except where due acknowledgement is made in the thesis. Any contribu- tion made to the research by others, with whom I have worked at UNSW or elsewhere, is explicitly acknowledged in the thesis. I also declare that the intellectual content of this thesis is the product of my own work, except to the extent that assistance from others in the project’s design and conception or in style, presentation and linguistic expression is acknowledged.’ Signed: ! " # $%& ' % ! ( ) ) ) " * ( ) ) + , -. -/ 0 -1 0 2/ ! % , 3 4 % % 5 6 7 /.18 + ' !"!# $ Abstract nowledge of anatomy is an elementary step towards the understanding K of the human body. First used by Alphonse Bertillon as an identification system, anthropometry refers to the measurements of human individuals. In orthopaedics, comparative analysis is widely used in the understanding of morphological variance due to races, sex and pathological conditions. The characterization of bone and joint geometry has also been a foundation of modern surgical implant design. Traditional anthropometric studies rely on physical measurements by means of osteometric table. Recent advancements of 3-D imaging modalities and image processing techniques have empowered more fine-grained anthropometric characterization. The inspiration for the study is: • the understanding of anatomy originating from the clinical domain have shown to contribute to undesirable inconsistency in the image processing domain. • the difficulty of existing automated anthropometric methodology in han- dling pathological femur. • the tedious amount of manual and subjective work involved with the increasing amount of high resolution imaging data. The aim of the study is to: • develop a consistent and robust methodology in accurate extraction of anthropometric parameters on the femur. i • increase the level of automation on the process of anthropometric pa- rameter extraction. With the bridging of anthropometry and the image processing disciplines, a robust methodology of anthropometric parameter extraction with high level of automation was developed, implemented and tested. A dataset comprised of femoral CT scans of 19 healthy Australian, 10 healthy Japanese, 15 Japanese diagnosed with primary or secondary hip osteoarthritis and 20 adult sheep was utilized for testing. Intra-class correlation and Cronbach’s α were extensively employed to evaluate the intra-rater, inter- rater and repeated scans consistency of the proposed methodology. High correlation values (mean > 0.95) were noted suggesting a high consistency of the methodology. All healthy and osteoarthritis human datasets were processed successfully. With the structural similarity between the sheep and human femur, the robustness was further demonstrated by accurate processing of the sheep dataset without the need of any modification of the underlying methodology. The methodology proposed is highly automated and requires very few user interactions in the parameter extraction stage. ii Acknowledgments his work would not have been possible without the continue support of T my supervisor, Prof. W.R. Walsh, and all fellow members of the Surgical & Orthopaedic Research Laboratories. I would like to express my sincere gratitude to Dr. Akira Maeyama for his gracious help on acquiring patient data overseas. I cannot say how grateful I am with my parents, for their values, their character and their unfailing support throughout the years. To my lovely sister Angela, for all her encouragements. Last, I wish to thank my dear uncle Simon, aunt Mary, and my cousins Joyce, Patrick and little Winnie for all the care and joy you bring during my stay in Australia. iii iv Contents 1. Introduction 1 2. Anatomy and Bone Histology 5 2.1. Histology of Bone .............................. 5 2.1.1. Types of Cells ............................ 6 2.1.2. Bone Salt .............................. 6 2.1.3. Woven and Lamellar Bone .................... 7 2.1.4. Cortical and Trabecular Bone ................. 8 2.1.5. Modelling and Remodelling ................... 9 2.2. Anatomy of the Human Femur ..................... 10 2.2.1. Hip Bone ............................... 10 2.2.2. Femur ................................ 11 2.2.2.1. Upper End ........................ 11 2.2.2.2. Shaft ............................ 14 2.2.2.3. Lower End ........................ 15 2.2.2.4. Bone Structure ..................... 15 2.2.3. Proximal Tibia ........................... 16 2.2.4. Patella ................................ 16 3. Medical Imaging 19 3.1. Overview ................................... 20 3.2. X-ray Imaging ................................ 20 3.2.1. Principles .............................. 21 3.2.2. Measurement Units ........................ 23 3.2.3. Generation of X-rays ....................... 23 3.2.4. Applications in Radiology .................... 24 v Contents 3.2.5. Biological Hazards ......................... 25 3.2.6. Strengths and Limitations .................... 25 3.3. Computed Tomography .......................... 26 3.3.1. Principle ............................... 26 3.3.2. Hounsfield Unit Scale ....................... 27 3.3.3. Quantitative Computed Tomography ............. 28 3.3.4. Applications in Radiology .................... 28 3.3.5. Biological Hazards ......................... 28 3.3.6. Strengths and Limitations .................... 29 3.3.6.1. Beam Hardening .................... 29 3.3.6.2. Partial Volume Averaging .............. 30 3.3.6.3. Photon Starvation ................... 30 3.3.6.4. Metal Objects ...................... 31 3.3.6.5. Ring Artifacts ...................... 32 3.3.6.6. Helical Artifacts .................... 32 3.4. Dual Energy X-ray Absorptiometry .................. 32 3.4.1. DXA Scores ............................. 34 3.4.2. Biological Hazard ......................... 35 3.4.3. Strengths and Limitations .................... 35 3.5. Magnetic Resonance Imaging ...................... 35 3.5.1. Principles .............................. 36 3.5.2. Biological Hazards ......................... 36 4. Image Analysis 39 4.1. Overview ................................... 40 4.2. Image Acquisition ............................. 40 4.2.1. The DICOM Format ........................ 40 4.3. Image Segmentation ............................ 41 4.3.1. Thresholding ............................ 41 4.3.1.1. Fixed Global Threshold ................ 42 4.3.1.2. Adaptive Threshold .................. 43 4.3.2. Region Growing .......................... 44 4.3.3. Edge Detection ........................... 45 4.3.3.1. Gradient Operators .................. 47 4.3.3.2. Laplacian Operator .................. 51 4.3.3.3. Canny Edge Detector ................. 56 4.3.4. Model Based Techniques ..................... 58 4.4. Image Geometric Transformation .................... 59 vi Contents 4.4.1. Affine Transformation ...................... 59 4.5. Morphological Processing ......................... 62 4.5.1. Preliminaries ............................ 62 4.5.2. Dilation and Erosion ....................... 64 4.5.2.1. Dilation .......................... 64 4.5.2.2. Erosion .......................... 65 4.5.3. Opening and Closing ....................... 66 4.5.4. The Hit-or-miss Operation ...................
Load more

Recommended publications
  • Vide. Specific Exercises and Activities Are Listed for the Various Physical Deviations
    DOCUMENT RESUME ED 051 216 SP 007 315 AUTHOR Muller, Robert M. TITLE Adaptive Physical Education. INSTITUTION Bensalam Township School District, Cornwolls Heights, Pa. PUB DATE riov 70 NOTE 46p. EDRS PRICE EDRS Price MP-$O.65 BC-$3.29 DESCRIPTORS *Curriculum Guides, *Elementary School Curriculum, Handicapped Students, *Physical Education, *Physically Handicapped, *School Health Services ABSTRACT GRADES OR AGES: Elementary grades. SUBJECT MATTER: Adaptive physical education. ORGANIZATION AND PHYSICAL APPEARANCE: The aims and objectives of the program and the screening procedure are described. Common postural deviations are identified and a number of congenital and other defects described. Details of the modified program are given. There is a glossary of terms and samples of letters to physicians and parents in connection with the program. The guide is mimeographed and spiral bound with a sott cover. OBJECTIVES AND ACTIVITIES: The objectives are briefly outlined at the beginning of the 'vide. Specific exercises and activities are listed for the various physical deviations. INSTRUCTIONAL MATERIALS: There is no information on materials. STUDENT ASSESSMENT: No provision is made for evaluation. (MBM) VS. DEPARiMENT OF HEALTH, LCUCATIDN & WELFARE OFFICE OF EDUL,ATION THIS DOCUMENT HA:, BEES REPRO- DUCED Ex,ArTLY AS RECEIVED FROM THE PERSON 09 ORGAN,ZAT1ON ORIG, INATIND IT PO.NTS OF VIEW OR OPIN- IONS STATED CO NOT NECESSAMIT REPRESENT OFF,CIAL OFF.CE OF EDO- CATION POSITION OR MUD' \:7 HYSICAL FDUCATION FOREWORD We believe all students should participate in a planned program of physical education.It ie the ultimate goal of the Adaptive Physical Education Department to provide every student with such a program, Adaptive Physical Eduction can offer helpful services to handicapped students so they can live and function more ef- fectively.All studrnts ,tending school should have the oppor- tunity to achieve a maximum of growth wad development.
    [Show full text]
  • 24/7 Nurseline Audio Health Topics
    24/7 Nurseline Audio Health Topics What are audio health topics? Health care questions and concerns are present even when symptoms are not. The 24/7 Nurseline audio health topics are available to help you and your family educate yourselves about many common and chronic illnesses and diseases — 24 hours a day, 7 days a week. Pre-recorded messages on topics provide the information you need to help: • Prevent illness • Identify warning signs • Administer self care How can I listen to audio health topics? It’s easy, just call the same toll-free number you call to speak with a nurse. You can call anytime for information on a variety of health care topics. If you are calling from a touchtone phone, just follow the directions below. If you are calling from a dial phone (rotary phone), please stay on the line and a nurse can direct you to a topic. Call instructions: • Look up the 4-digit number for the topic you want to hear. • Call the toll-free number. While listening to a topic, you can activate • Select the option for audio health topics. You will be transferred the following options by pressing the to an agent who can connect you to the appropriate recording. corresponding key on your telephone keypad. • Listen to the recording. Topics are usually 2 to 5 minutes Press 0 to speak to a nurse. in length. Press 1 to replay the entire topic. Press 9 to end the call. Call the 24/7 Nurseline at 800-581-0393 to access audio health topics.
    [Show full text]
  • Ectodermal Dysplasia Syndrome with Cleft Palate, Hypodontia, Metatarsus Adductus and Imperforate Anus: a New Syndrome?
    Ectodermal Dysplasia Syndrome ORAL MEDICINE ECTODERMAL DYSPLASIA SYNDROME WITH CLEFT PALATE, HYPODONTIA, METATARSUS ADDUCTUS AND IMPERFORATE ANUS: A NEW SYNDROME? 1UMAIR KHAN, BDS, C-Radiology (UK), MSc Oral Medicine (EDI-UCL, UK),MIAOMT (USA), MBSOM (UK) 2RABIA AZIZ, BDS 3GHAZALA HASSAN, BDS 4TAHIRA ZAFAR, BDS 5SAHAR IQRAR, BDS ABSTRACT Ectodermal dysplasia constitute a large group of rare, heterogenous (under clinical and genetic aspects), congenital/hereditary disorders characterized by a constellation of findings involving a primary defect (hypoplasia or aplasia) in at least two embryonic ectodermal-derived tissues including the teeth, skin, appendageal structures, hair, nails, nerve cells, eccrine glands, sebaceous glands and parts of the eye (conjunctiva), ear, and certain other structures. More than 192 distinct disorders have been described. The most common Ectodermal dysplasias are X-linked recessive hypohidrotic/ anhidrotic type known as Christ-Siemens Touraine syndrome with the gene mapping to Xq12-q13 and hydrotic type known as Clouston’s syndrome. Several ED syndromes may manifest in association with midfacial defects, mainly cleft palate and/or lip. Hypodontia of the primary and permanent dentition is the most common oral finding. This study presents four cases of the same family, two suffering from Ectodermal dysplasia along with hypodontia and cleft palate, one of which also presents metatarsus adductus and imperforate anus (proband) and the remaining two out of four with hypodontia in the absence of ectodermal dysplasia, one of which also presents metatarsus adductus (elder sibling) with imperforate anus in the other (youngest sibling). Oral and Maxillofacial Physicians & Dentists can be the first to diagnose ectodermal dysplasia due to the presence of specific facio-oral features and absence of teeth respectively.
    [Show full text]
  • “When Our Feet Hurt, We Hurt All Over.”
    Search Doctors/ what a relief! About Us Products Services Referrers Downloads F.A.Q. Home “When our feet hurt, With a highly experienced team of foot care providers at your service, we hurt all over.” the Foot Power clinic in Sydney’s Dee Why offers innovative foot care solutions. Put simply, at Foot Power we put feet first. Socrates Your feet are your body’s foundation so give them the best possible care and get the most from your body. Back pain, aching joints and foot discomfort can all be signs that your feet are in need of some TLC! A visit to the Foot Power clinic can help you reduce your discomfort, train effectively and get back in the game! Contact Us | Useful Links © Footpower 2009 | Site Map Search Doctors/ what a relief! About Us Products Services Referrers Downloads F.A.Q. Home “When our feet hurt, With a highly experienced team of foot care providers at your service, we hurt all over.” the Foot Power clinic in Sydney’s Dee Why offers innovative foot care solutions. Put simply, at Foot Power we put feet first. Socrates Your feet are your body’s foundation so give them the best possible care and get the most from your body. Back pain, aching joints and foot discomfort can all be signs that your feet are in need of some TLC! A visit to the Foot Power clinic can help you reduce your discomfort, train effectively and get back in the game! Contact Us | Useful Links © Footpower 2009 | Site Map Search Doctors/ what a relief! About Us Products Services Referrers Downloads F.A.Q.
    [Show full text]
  • Korean Knee Society Terminology Book For
    Korean Knee Society’s Terminology Book This edition first published 2015 © 2015 by Korean Knee Society. Published edition © 2015 Wiley Publishing Japan K.K. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the copyright owner. ISBN: 978-4-939028-29-8 Published by Wiley Publishing Japan K.K. Tokyo Office: Frontier Koishikawa Bldg. 4F, 1-28-1 Koishikawa, Bunkyo-ku, Tokyo 112-0002, Japan Telephone: 81-3-3830-1221 Fax: 81-3-5689-7276 Internet site: http://www.wiley.com/wiley-blackwell e-mail: [email protected] Printed and bound in Korea by JEIL PRINTECH 발 간 사 대부분의 의학 용어는 영어에서 유래되어 그 해석과 의미가 오 랜 시간 동안 계승 발전되어 왔습니다. 그러나 오랜 역사를 거 치면서 용어의 해석이 다양해져 교육 현장은 물론 임상에서도 여러 용어로 혼용되고 있어 ‘용어 통일’의 필요성이 지속적으로 대두되어 왔습니다. 이에 대한슬관절학회에서는 슬관절 분야 에서 많이 쓰이고 있는 용어들을 수집하여 용어를 재정비 하고 통일하는 사업을 추진하였습니다. 대한슬관절학회 교과서편찬위원회에서는 2013년 12월에 업무를 개시하여 1년 5 개월 동안 슬관절 분야의 대표적 영어 교과서의 색인, 대한정형외과학회 교과서 색 인 및 용어집, 대한슬관절학회 교과서 편찬시 논의 된 용어통일 리스트에서 용어를 수집하여 약 5,000 여개의 주요 용어를 정리하였습니다. 이번 용어 편찬 작업에서 주목할 만한 부분은 관련 전문가들은 물론 일반인들도 용 어 해석을 쉽게 찾아볼 수 있도록 어플리케이션을 제작하여 앱 스토어나 플레이 스 토어에서 무료로 다운로드 하여 볼 수 있도록 접근성을 높였다는 것입니다. 이번 용 어집 편찬 작업이 선생님들의 진료와 연구에 도움이 되고, 일반인들도 보다 쉽고 정 확하게 의료진들과 소통할 수 있길 바라며 앞으로 꾸준히 발전해 나갈 수 있도록 많 은 관심 바랍니다.
    [Show full text]
  • Freedom and Negativity in the Works of Samuel Beckett and Theodor Adorno
    FREEDOM AND NEGATIVITY IN THE WORKS OF SAMUEL BECKETT AND THEODOR ADORNO Natalie Leeder Royal Holloway, University of London PhD Thesis TABLE OF CONTENTS DECLARATION OF ACADEMIC INTEGRITY ........................................................................... 3 ABSTRACT ........................................................................................................................ 4 ACKNOWLEDGEMENTS ...................................................................................................... 5 ABBREVIATIONS ................................................................................................................ 6 INTRODUCTION ................................................................................................................ 9 CHAPTER ONE: FREEDOM AND ITS LIMITS ...................................................................... 44 CHAPTER TWO: THE ILLUSION OF FREEDOM AND THE FREEDOM OF ILLUSION ................ 71 CHAPTER THREE: THE SCARS OF EVIL .......................................................................... 105 CHAPTER FOUR: VIRTUAL FREEDOM ............................................................................ 144 CHAPTER FIVE: METAPHYSICS ..................................................................................... 190 EPILOGUE .................................................................................................................... 227 BIBLIOGRAPHY ............................................................................................................
    [Show full text]
  • The NEW Psoas Release Party! Release Your Body from Chronic Pain and Discomfort
    The NEW Psoas Release Party! Release Your Body From Chronic Pain and Discomfort by Jonathan FitzGordon Copyright © 2015 Yoga Center of Brooklyn, LLC – ii – Other books in this series: Sciatica/Piriformis Syndrome The Spine: An Introduction To The Central Channel The Exercises of CoreWalking CoreWalking: First Steps to A New Yourself Although every effort has been made to provide an accurate description of posture remedies and their benefits, the information contained herein is not intended to be a substitute for professional medical advice, diagnosis or treatment in any manner. Always consult your physician or health care professional before performing any new exercise or exercise technique, particularly if you are pregnant, nursing, elderly, or if you have any chronic or recurring conditions. The authors are not responsible or liable for any injuries occurred by performing any of the exercises given or diagnosis made by a user based on the information shown within this document. Cover Illustation: Frank Morris – iii – TABLE OF CONTENTS I The Wonder Muscle ......................................1 II The Psoas in Infancy ...................................13 III The Psoas Is a Pulley ...................................21 IV Muscles That Support the Psoas ...............31 V The Effects of a Tight Psoas ........................47 VI The Psoas and the Organs .......................... 53 VII The Psoas and the Nervous System ..........59 VIII Releases .........................................................67 IX Stretches ......................................................... 89 X Psoas Blog Posts ...........................................99 Acknowledgements ............................................257 – v – Jonathan FitzGordon FOUR VIEWS OF THE PSOAS MUSCLE Psoas Major – vi – Chapter I THE WONDER MUSCLE As a yoga teacher, I was taught to stretch peo- ple, but it wasn’t long before I began to come across people who didn’t seem to be served by stretching.
    [Show full text]
  • The Results of Posteromedial Release in Clubfoot Below the Age of 3 Years
    International Journal of Recent Trends in Science And Technology, ISSN 2277-2812 E-ISSN 2249-8109, Volume 10, Issue 3, 2014 pp 486-491 The Results of Posteromedial Release in Clubfoot below the Age of 3 Years Ronald Joseph Menezes 1, Rakesh Sera 2 1Associate Professor, 2PG Resident Department of Orthopaedics, Father Muller Medical College, Kankanady, Mangalore – 575 002, Karnataka, INDIA. Corresponding Addresses: [email protected] , [email protected] Research Article Abstract: Specific objectives: Congenital Talipes outcome. Controlled differential fractional distraction by the Equinovarus(Clubfoot) is one of the most common foot anomalies application of JESS is more suitable for the correction of relapsed which can be treated by serial casting technique with high rate of cases, than second surgical procedures. Since we treated only 4 success. Surgery is indicated for deformities that do not respond to cases by this method, it is difficult to comment on the final conservative treatment or the patients that seek medical outcome intervention too late. In this study, we reviewed the results of Keywords : Congenital talipes equinovarus, posteromedial release. posteromedial release in clubfoot below 3 years. Materials and methods : Between May 2009 to June 2013, we treated sixty four Introduction feet (64) with idiopathic CTEV in forty (40) children who were Idiopathic congenital talipes equinovarus (clubfoot) is a below 3 years, who were evaluated and operated using common complex deformity that occurs in approximately posteromedial release in Father Muller Medical College Hospital, one or two per 1000 newborns 1. The long-term goal of Mangalore. All the feet were given a trial of serial manipulation treatment is a functional, pain-free, plantigrade foot with and cast application till the deformities were no more correctable.
    [Show full text]
  • Lecture 8. Anatomic and Physiological Features of Bone and Muscular System at Children
    ODESSA NATIONAL MEDICAL UNIVERSITY Department of propedeutics of pediatrics Lecture 8. Anatomic and physiological features of bone and muscular system at children. Semiotics of defeat and diseases of bone and muscular system. Substantiation of the topic: • Knowledge of the anatomical and physiological features of the bony and muscle system in children. Semiotics of the affections and diseases of the bony and muscle system is an actual problem due to its prevalence, diversity of clinical symptoms, often hidden proceeding with the following progress. • Development of bone precursor cells. Bone precursor cells are divided into developmental stages, which are 1. mesenchymal stem cell, 2. pre-osteoblast, 3. osteoblast, and 4. mature osteocytes, and 5. osteoclast. • The bonу ѕyѕtem (skeleton, ѕkeletal ѕyѕtem) beginѕ to develop at the second month of the intrauterine life. •The cartilage tissue is formed from the congeѕtion of mesenchуmal cellѕ, in which on 5- 7-th week the pointѕ of oѕѕification appear. • By the time of birth the meѕenchymal cellѕ uѕually diѕappear. • The proceѕѕ of oѕѕification beginѕ during the prenatal period and it takeѕ place in the dіaрhуses of the long boneѕ and ѕome epiphyѕeѕ (top and lower capitulum of the hip bone, top capitulum of the tibia, cubiformi bone). The ѕkeleton iѕ completely developed when 806 nucleuѕeѕ of oѕѕification appear. Idiopatic osteopsatirosis • As a reѕult of anomalieѕ of the ѕkeleton embryogeneѕiѕ varіous dіseases can develop. In particular, aѕ the reѕult of reduced oѕteoblaѕtic activity in the bony tіssue (as it iѕ conѕidered, at the expense of the inhibition of the calcification рrocesses bу the collagen of the bony tіsѕue) a heredіtarу diѕeaѕe of the ѕkeleton with the dominant type of inheritance can develop - the imperfect oѕteogeneѕiѕ, that manifeѕtѕ in frequent and plural fractures.There are 2 forms- imperfect oѕteogeneѕiѕ & idiopatic osteopsatirosis.
    [Show full text]
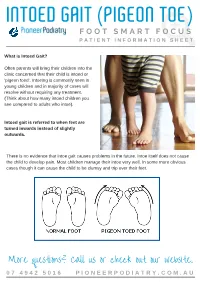
  • Intoed Gait (Pigeon Toe) F O O T S M a R T F O C U S P a T I E N T I N F O R M a T I O N S H E E T
    INTOED GAIT (PIGEON TOE) F O O T S M A R T F O C U S P A T I E N T I N F O R M A T I O N S H E E T What is Intoed Gait? Often parents will bring their children into the clinic concerned that their child is intoed or ‘pigeon toed’. Intoeing is commonly seen in young children and in majority of cases will resolve without requiring any treatment. (Think about how many intoed children you see compared to adults who intoe). Intoed gait is referred to when feet are turned inwards instead of slightly outwards. There is no evidence that intoe gait causes problems in the future. Intoe itself does not cause the child to develop pain. Most children manage their intoe very well. In some more obvious cases though it can cause the child to be clumsy and trip over their feet. More questions? Call us or check out our website. 0 7 4 9 4 2 5 0 1 6 P I O N E E R P O D I A T R Y . C O M . A U INTOED GAIT (PIGEON TOE) F O R T H E D O C T O R C L I N I C A L P R A C T I C E G U I D E L I N E What causes Intoed Gait? More insidious causes of intoeing should be ruled out and may include cerebal palsy and hip dysplasia. In healthy children, the three most common causes of intoeing come from either the level of the foot, leg or hip: Metatarsus Adductus – most common cause in an infant.
    [Show full text]
  • The Effect of a Corrective Exercise Program on Ninth Grade Boys with Foot Deviations
    Central Washington University ScholarWorks@CWU All Master's Theses Master's Theses 1964 The Effect of a Corrective Exercise Program on Ninth Grade Boys with Foot Deviations Bill Hand Central Washington University Follow this and additional works at: https://digitalcommons.cwu.edu/etd Part of the Educational Methods Commons Recommended Citation Hand, Bill, "The Effect of a Corrective Exercise Program on Ninth Grade Boys with Foot Deviations" (1964). All Master's Theses. 389. https://digitalcommons.cwu.edu/etd/389 This Thesis is brought to you for free and open access by the Master's Theses at ScholarWorks@CWU. It has been accepted for inclusion in All Master's Theses by an authorized administrator of ScholarWorks@CWU. For more information, please contact [email protected]. THE Kl!,FECT 0]1 A COHRECTIVE EXERCISE PROGRALI ON NINTH GRADE BOYS WITH FOOT DEVIATIONS A Thesis l-'resented to The Graduate Faculty Central Washington State College In Partial Fulfillment Of the Requirements for the Degree Master of Education by Bill Hand July 1964 2''_:,)f?CH i·tu.g a:'I APPROVED FOR THE GRADUATE FACULTY ________________________________ A. H. Poffenroth, COMMITTEE CHAIRMAN _________________________________ L. E. Reynolds _________________________________ Mary Bowman ii ACKNO',/LEDGEMENTS I wish to acknowledge the advice and understanding given by Dr. Mary Bowman, Committee Chairman. Appreciation is also due my sister, Sarah, for as­ sistance and encouragement during the writing of this paper. iii TABLE OF CONT}}I';rTS CHAPTER PAGE I. THE PROBLEM AND DEFINITIONS OF '.I.'ERMS. • 1 Statement of the Problem. • . 1 Importance of the Study • • . 1 Limitations of the Study.
    [Show full text]
  • Yoga for a HAPPY BACK Practicing Yoga for Better Physical Health for a HAPPY BACK and Understanding the Role of the Mind- Body Connection in Back Pain
    YOGA Learn how to heal back and spinal I request that you read this book problems through yoga therapy with this carefully, imbibe its contents, unique framework. Combining detailed and practice the techniques. One day instruction on evaluation of conditions you will look back and be glad you did. and treatment techniques with personal YOGA —from the foreword by Aadil Palkhivala, narrative and case studies, Yoga for a Yoga-Asana Master, Happy Back bridges the gap between Co-founder of Purna Yoga FOR A HAPPY BACK practicing yoga for better physical health FOR A HAPPY BACK and understanding the role of the mind- body connection in back pain. Krentzman’s DVD by the same name has been a powerful A Teacher’s Guide to Utilizing her vast experience as a resource for patients and professional physical therapist and yoga therapist, colleagues of mine for many years. Now Spinal Health through and the latest advances in the field they all have an opportunity to dive of yoga therapy, Rachel Krentzman deeply into not only the how but even advises how to design therapeutic yoga more importantly the why her approach Yoga Therapy classes for individuals with back pain of makes so many backs happy! all forms. She includes information on —Matthew J. Taylor, PT, PhD, Past President creating class themes and never before of IAYT, Matthew J. Taylor Institute, published sequences from the Purna www.smartsafeyoga.com RACHEL yoga tradition for alignment-based treatment of specific spinal conditions. With over 300 photos and illustrations, KRENTZMAN PT, E-RY T teachers can access the benefits of yoga Foreword by Aadil Palkhivala therapy for the treatment of orthopedic conditions and to promote general RACHEL KRENTZMAN is spinal health.
    [Show full text]