Author's Personal Copy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Potential Vorticity Dynamics and Tropopause Fold
POTENTIAL VORTICITY DYNAMICS AND TROPOPAUSE FOLD M.D. ANDREI1,2, M. PIETRISI1,2, S. STEFAN1 1 University of Bucharest, Faculty of Physics, P.O.BOX MG 11, Magurele, Bucharest, Romania Emails: [email protected]; [email protected] 2 National Meteorological Administration, Bucuresti-Ploiesti Ave., No. 97, 013686, Bucharest, Romania Received November 1, 2017 Abstract. Extra tropical cyclones evolution depends a lot on the dynamically and thermodynamically interactions between the lower and the upper troposphere. The aim of this paper is to demonstrate the importance of dynamic tropopause fold in the development of a cyclone which affected Romania in 12th and 13th of November, 2016. The coupling between a positive potential vorticity anomaly and the jet stream has caused the fall of dynamic tropopause, which has a great influence in the cyclone deepening. This synoptic situation has resulted in a big amount of precipitation and strong wind gusts. For the study, ALARO limited area spectral model analyzes (e.g., 300 hPa Potential Vorticity, 1,5 PVU field height, 300 hPa winds, mean sea level pressure), data from the Romanian National Meteorological Administration meteorological stations, cross-sections and satellite images (water vapor and RGB) were used. Accordingly, the results of this study will be used in operational forecast, for similar situations which would appear in the future, and can improve it. Key words: potential vorticity, tropopause fold, cyclone. 1. INTRODUCTION Dynamic tropopause is the 1.5 or 2 PVU (potential vorticity units) surface that separates the dry, stable, stratospheric air from the humid, unstable, tropospheric air [1]. The dynamic tropopause fold corresponds to a positive potential vorticity anomaly, with high amplitude in the upper troposphere [2, 3], which induces a cyclonic circulation that propagates to the surface and reduce, under it, static stability. -

Potential Vorticity Diagnosis of a Simulated Hurricane. Part I: Formulation and Quasi-Balanced Flow
1JULY 2003 WANG AND ZHANG 1593 Potential Vorticity Diagnosis of a Simulated Hurricane. Part I: Formulation and Quasi-Balanced Flow XINGBAO WANG AND DA-LIN ZHANG Department of Meteorology, University of Maryland at College Park, College Park, Maryland (Manuscript received 20 August 2002, in ®nal form 27 January 2003) ABSTRACT Because of the lack of three-dimensional (3D) high-resolution data and the existence of highly nonelliptic ¯ows, few studies have been conducted to investigate the inner-core quasi-balanced characteristics of hurricanes. In this study, a potential vorticity (PV) inversion system is developed, which includes the nonconservative processes of friction, diabatic heating, and water loading. It requires hurricane ¯ows to be statically and inertially stable but allows for the presence of small negative PV. To facilitate the PV inversion with the nonlinear balance (NLB) equation, hurricane ¯ows are decomposed into an axisymmetric, gradient-balanced reference state and asymmetric perturbations. Meanwhile, the nonellipticity of the NLB equation is circumvented by multiplying a small parameter « and combining it with the PV equation, which effectively reduces the in¯uence of anticyclonic vorticity. A quasi-balanced v equation in pseudoheight coordinates is derived, which includes the effects of friction and diabatic heating as well as differential vorticity advection and the Laplacians of thermal advection by both nondivergent and divergent winds. This quasi-balanced PV±v inversion system is tested with an explicit simulation of Hurricane Andrew (1992) with the ®nest grid size of 6 km. It is shown that (a) the PV±v inversion system could recover almost all typical features in a hurricane, and (b) a sizeable portion of the 3D hurricane ¯ows are quasi-balanced, such as the intense rotational winds, organized eyewall updrafts and subsidence in the eye, cyclonic in¯ow in the boundary layer, and upper-level anticyclonic out¯ow. -

(Potential) Vorticity: the Swirling Motion of Geophysical Fluids
(Potential) vorticity: the swirling motion of geophysical fluids Vortices occur abundantly in both atmosphere and oceans and on all scales. The leaves, chasing each other in autumn, are driven by vortices. The wake of boats and brides form strings of vortices in the water. On the global scale we all know the rotating nature of tropical cyclones and depressions in the atmosphere, and the gyres constituting the large-scale wind driven ocean circulation. To understand the role of vortices in geophysical fluids, vorticity and, in particular, potential vorticity are key quantities of the flow. In a 3D flow, vorticity is a 3D vector field with as complicated dynamics as the flow itself. In this lecture, we focus on 2D flow, so that vorticity reduces to a scalar field. More importantly, after including Earth rotation a fairly simple equation for planar geostrophic fluids arises which can explain many characteristics of the atmosphere and ocean circulation. In the lecture, we first will derive the vorticity equation and discuss the various terms. Next, we define the various vorticity related quantities: relative, planetary, absolute and potential vorticity. Using the shallow water equations, we derive the potential vorticity equation. In the final part of the lecture we discuss several applications of this equation of geophysical vortices and geophysical flow. The preparation material includes - Lecture slides - Chapter 12 of Stewart (http://www.colorado.edu/oclab/sites/default/files/attached- files/stewart_textbook.pdf), of which only sections 12.1-12.3 are discussed today. Willem Jan van de Berg Chapter 12 Vorticity in the Ocean Most of the fluid flows with which we are familiar, from bathtubs to swimming pools, are not rotating, or they are rotating so slowly that rotation is not im- portant except maybe at the drain of a bathtub as water is let out. -

Potential Vorticity
POTENTIAL VORTICITY Roger K. Smith March 3, 2003 Contents 1 Potential Vorticity Thinking - How might it help the fore- caster? 2 1.1Introduction............................ 2 1.2WhatisPV-thinking?...................... 4 1.3Examplesof‘PV-thinking’.................... 7 1.3.1 A thought-experiment for understanding tropical cy- clonemotion........................ 7 1.3.2 Kelvin-Helmholtz shear instability . ......... 9 1.3.3 Rossby wave propagation in a β-planechannel..... 12 1.4ThestructureofEPVintheatmosphere............ 13 1.4.1 Isentropicpotentialvorticitymaps........... 14 1.4.2 The vertical structure of upper-air PV anomalies . 18 2 A Potential Vorticity view of cyclogenesis 21 2.1PreliminaryIdeas......................... 21 2.2SurfacelayersofPV....................... 21 2.3Potentialvorticitygradientwaves................ 23 2.4 Baroclinic Instability . .................... 28 2.5 Applications to understanding cyclogenesis . ......... 30 3 Invertibility, iso-PV charts, diabatic and frictional effects. 33 3.1 Invertibility of EPV ........................ 33 3.2Iso-PVcharts........................... 33 3.3Diabaticandfrictionaleffects.................. 34 3.4Theeffectsofdiabaticheatingoncyclogenesis......... 36 3.5Thedemiseofcutofflowsandblockinganticyclones...... 36 3.6AdvantageofPVanalysisofcutofflows............. 37 3.7ThePVstructureoftropicalcyclones.............. 37 1 Chapter 1 Potential Vorticity Thinking - How might it help the forecaster? 1.1 Introduction A review paper on the applications of Potential Vorticity (PV-) concepts by Brian -

A Vorticity-And-Stability Diagram As a Means to Study Potential Vorticity
https://doi.org/10.5194/wcd-2021-31 Preprint. Discussion started: 29 June 2021 c Author(s) 2021. CC BY 4.0 License. A vorticity-and-stability diagram as a means to study potential vorticity nonconservation Gabriel Vollenweider1, Elisa Spreitzer1, and Sebastian Schemm1 1Institute for Atmospheric and Climate Science, ETH Zürich, Zürich, Switzerland Correspondence: Sebastian Schemm ([email protected]) Abstract. The study of atmospheric circulation from a potential vorticity (PV) perspective has advanced our mechanistic understanding of the development and propagation of weather systems. The formation of PV anomalies by nonconservative processes can provide additional insight into the diabatic-to-adiabatic coupling in the atmosphere. PV nonconservation can be driven by changes in static stability, vorticity or a combination of both. For example, in the presence of localized latent heating, 5 the static stability increases below the level of maximum heating and decreases above this level. However, the vorticity changes in response to the changes in static stability (and vice versa), making it difficult to disentangle stability from vorticity-driven PV changes. Further diabatic processes, such as friction or turbulent momentum mixing, result in momentum-driven, and hence vorticity-driven, PV changes in the absence of moist diabatic processes. In this study, a vorticity-and-stability diagram is introduced as a means to study and identify periods of stability- and vorticity-driven changes in PV. Potential insights and 10 limitations from such a hyperbolic diagram are investigated based on three case studies. The first case is an idealized warm conveyor belt (WCB) in a baroclinic channel simulation. The simulation allows only condensation and evaporation. -

Tropical Cyclone Motion
Tropical Cyclone Motion Introduction To first order, tropical cyclone motion is modulated by the large-scale flow. In the following, we aim to conceptually and mathematically describe this influence. Additional contributions to tropical cyclone motion arise from meso- to synoptic-scale asymmetries driven by a multitude of factors. This lecture closes by describing such asymmetries as well as discussing how and why they impact tropical cyclone motion. Key Concepts • What are the factors controlling tropical cyclone motion? • How do these factors vary as a function of tropical cyclone intensity? Climatological Perspective on Tropical Cyclone Motion To first order, tropical cyclones track around the periphery of subtropical anticyclones. In this sense, tropical cyclones originate in the tropics and either 1) track westward to landfall or colder waters and ultimate dissipation or 2) turn poleward and eastward (recurve) into the midlatitudes, ultimately dissipating or undergoing extratropical transition. The global mean latitude of recurvature, defined as the latitude at which the tropical cyclone no longer has a westward component of motion, is approximately 25° (higher in the Northern Hemisphere) The meridional component of motion of tropical cyclones is typically poleward from genesis and increases in magnitude as tropical cyclones enter the midlatitudes. Average translation speeds are quite low in the tropics (~10 kt) but increase rapidly with increasing distance from the Equator; there is greater variability in translation speed for eastward-moving tropical cyclones versus their westward- moving counterparts. Given that track forecast errors are proportional to translation speed, this implies that larger track forecast errors may be expected for tropical cyclones recurving into the midlatitudes. -

An Introduction to Dynamic Meteorology.Pdf
January 24, 2004 12:0 Elsevier/AID aid An Introduction to Dynamic Meteorology FOURTH EDITION January 24, 2004 12:0 Elsevier/AID aid This is Volume 88 in the INTERNATIONAL GEOPHYSICS SERIES A series of monographs and textbooks Edited by RENATADMOWSKA, JAMES R. HOLTON and H.THOMAS ROSSBY A complete list of books in this series appears at the end of this volume. January 24, 2004 12:0 Elsevier/AID aid AN INTRODUCTION TO DYNAMIC METEOROLOGY Fourth Edition JAMES R. HOLTON Department of Atmospheric Sciences University of Washington Seattle,Washington Amsterdam Boston Heidelberg London New York Oxford Paris San Diego San Francisco Singapore Sydney Tokyo January 24, 2004 12:0 Elsevier/AID aid Senior Editor, Earth Sciences Frank Cynar Editorial Coordinator Jennifer Helé Senior Marketing Manager Linda Beattie Cover Design Eric DeCicco Composition Integra Software Services Printer/Binder The Maple-Vail Manufacturing Group Cover printer Phoenix Color Corp Elsevier Academic Press 200 Wheeler Road, Burlington, MA 01803, USA 525 B Street, Suite 1900, San Diego, California 92101-4495, USA 84 Theobald’s Road, London WC1X 8RR, UK This book is printed on acid-free paper. Copyright c 2004, Elsevier Inc. All rights reserved. No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage and retrieval system, without permission in writing from the publisher. Permissions may be sought directly from Elsevier’s Science & Technology Rights Department in -

The Role of Mid-Level Vortex in the Intensification and Weakening Of
J. Earth Syst. Sci. (2017) 126:94 c Indian Academy of Sciences DOI 10.1007/s12040-017-0879-y The role of mid-level vortex in the intensification and weakening of tropical cyclones Govindan Kutty* and Kanishk Gohil Indian Institute of Space Science and Technology, Thiruvananthapuram 695 547, India. *Corresponding author. e-mail: [email protected] MS received 2 October 2016; revised 18 April 2017; accepted 25 April 2017; published online 6 October 2017 The present study examines the dynamics of mid-tropospheric vortex during cyclogenesis and quantifies the importance of such vortex developments in the intensification of tropical cyclone. The genesis of tropical cyclones are investigated based on two most widely accepted theories that explain the mechanism of cyclone formation namely ‘top-down’ and ‘bottom-up’ dynamics. The Weather Research and Forecast model is employed to generate high resolution dataset required for analysis. The development of the mid-level vortex was analyzed with regard to the evolution of potential vorticity (PV), relative vorticity (RV) and vertical wind shear. Two tropical cyclones which include the developing cyclone, Hudhud and the non-developing cyclone, Helen are considered. Further, Hudhud and Helen, is compared to a deep depression formed over Bay of Bengal to highlight the significance of the mid-level vortex in the genesis of a tropical cyclone. Major results obtained are as follows: stronger positive PV anomalies are noticed over upper and lower levels of troposphere near the storm center for Hudhud as compared to Helen and the depression; Constructive interference in upper and lower level positive PV anomaly maxima resulted in the intensification of Hudhud. -

Fluid Dynamics of the Atmosphere and Oceans
Fluid Dynamics of the Atmosphere and Oceans John Thuburn University of Exeter Introduction This module Fluid Dynamics of the Atmosphere and Oceans comprises 33 hours of lectures and examples classes. Outline of course content The equations of motion in a rotating frame; some conservation properties; circulation theorem; vorticity equation; potential vorticity equation. Hierarchies of approximate governing equations; balance and filtering. Shallow water equations: circulation and potential vorticity; energy and angular mo- mentum; gravity and Rossby waves; geostrophic balance; geostrophic adjustment; Rossby radius; quasigeostrophic shallow water equations; quasigeostrophic potential vorticity; Rossby waves; Kelvin waves. Boussinesq approximation; gravity waves in three dimensions; mountain waves; non- linear effects; eddy fluxes. Shallow atmosphere hydrostatic primitive equations, in different coordinate systems; conservation properties; Rossby and gravity waves. Quasigeostrophic theory in three dimensions: ageostrophic equations; quasigeostrophic potential vorticity equation; omega equation; free Rossby waves; Forced Rossby waves and the Charney Drazin theorem; eddy fluxes; surface waves on a potential temperature gradient; the Eady model of baroclinic instability. The planetary boundary layer; the Ekman spiral; Ekman pumping; Sverdrup balance. 1 1 Governing equations in vector form Du 1 + 2Ω u = p Φ; (1) Dt × −ρ∇ − ∇ ∂ρ + (ρu) = 0; (2) ∂t ∇ · DT p c + u = 0. (3) v Dt ρ∇ · 2 Governing equations in spherical polar coordi- nates Du uv tan φ uw 1 ∂p + 2Ωv sin φ + 2Ωw cos φ + = 0 (4) Dt − r r − ρr cos φ ∂λ Dv u2 tan φ vw 1 ∂p + + + 2Ωu sin φ + = 0 (5) Dt r r ρr ∂φ Dw u2 + v2 1 ∂p 2Ωu cos φ + g + = 0 (6) Dt − r − ρ ∂r ∂ρ + (ρu) = 0 (7) ∂t ∇ · DT p c + u = 0 (8) v Dt ρ∇ · where D ∂ u ∂ v ∂ ∂ + + + w (9) Dt ≡ ∂t r cos φ ∂λ r ∂φ ∂r 1 ∂u ∂(v cos φ) 1 ∂(r2w) u + + (10) ∇ · ≡ r cos φ ∂λ ∂φ r2 ∂r 2 3 Hierarchies of approximate equation sets (Quasi-)hydrostatic: Neglect Dw/Dt term. -

Diagnostic of Cyclogenesis Using Potential Vorticity
Atmósfera 19(4), 213-234 (2006) Diagnostic of cyclogenesis using potential vorticity H. A. BASSET and A. M. ALI Department of Astronomy and Meteorology, Faculty of Science, Al-Azhar University, Cairo, Egypt. Corresponding author: H. Basset; e-mail: [email protected] Received September 5, 2005; accepted February 12, 2006 RESUMEN En las latitudes medias los ciclones y los anticiclones son los sistemas meteorológicos dominantes a escala sinóptica. Una manera atractiva de estudiar los aspectos dinámicos de estas estructuras es utilizar el marco de la vorticidad potencial (PV). En este trabajo se investigan varios aspectos de la ciclogénesis de latitudes medias utilizando los análisis de un caso de estudio dentro de este marco. El análisis de la vorticidad asoluta, relativa y potencial implica la significancia de la dinámica de los niveles altos en la iniciación de este caso de ciclogénesis. Por un lado, el análisis de la vorticidad isobárica parece ser informativo, exacto y fácil de utilizar como método para describir la dinámica de los niveles altos. Por otro lado, el análisis de la PV proporciona una imagen resumida del desarrollo y la evolución en los niveles altos y bajos, lo que es directamente visible, con base en un número pequeño de gráficas comparado con el del análisis de la vorticidad isobárica. El despliegue de la secuencia de tiempo de la PV en la superficie isentrópica apropiada ayuda a entender fácilmente la dinámica tridimensional del desarrollo del nivel alto. ABSTRACT Cyclones and anticyclones are the dominant synoptic scale meteorological systems in midlatitudes. An attractive way to study dynamical aspects of these structures is provided by the use of potential vorticity (PV) framework. -

Absolute and Potential Vorticity in Convective Vortices Table 1
Atmos. Chem. Phys. Discuss., 9, 7531–7554, 2009 Atmospheric www.atmos-chem-phys-discuss.net/9/7531/2009/ Chemistry ACPD © Author(s) 2009. This work is distributed under and Physics 9, 7531–7554, 2009 the Creative Commons Attribution 3.0 License. Discussions This discussion paper is/has been under review for the journal Atmospheric Chemistry Absolute and and Physics (ACP). Please refer to the corresponding final paper in ACP if available. potential vorticity in convective vortices R. J. Conzemius and M. T. Montgomery Clarification on the generation of absolute and potential vorticity in mesoscale Title Page Abstract Introduction convective vortices Conclusions References R. J. Conzemius1,2 and M. T. Montgomery1,3 Tables Figures 1Department of Atmospheric Science, Colorado State University, Fort Collins, Colorado, USA J I 2WindLogics, Inc., Grand Rapids, Minnesota, USA 3 Naval Postgraduate School, Monterey, California, USA J I Received: 18 February 2009 – Accepted: 27 February 2009 – Published: 23 March 2009 Back Close Correspondence to: R. J. Conzemius ([email protected]) Full Screen / Esc Published by Copernicus Publications on behalf of the European Geosciences Union. Printer-friendly Version Interactive Discussion 7531 Abstract ACPD The purpose of this paper is to clarify what we think are several outstanding issues concerning the predominant mechanism of vorticity generation in mesoscale convec- 9, 7531–7554, 2009 tive vortices (MCVs). Using idealized mesoscale numerical simulations of MCV devel- 5 opment, we examine here the vertical vorticity budgets in order to quantify the con- Absolute and tributions of flux convergence of absolute vorticity versus tilting in the generation of potential vorticity in MCV vorticity. -
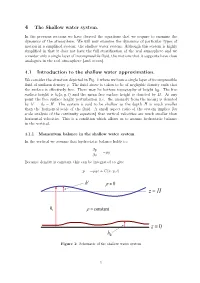
4 the Shallow Water System
4 The Shallow water system. In the previous sections we have derived the equations that we require to examine the dynamics of the atmosphere. We will now examine the dynamics of particular types of motion in a simplified system: the shallow water system. Although this system is highly simplified in that it does not have the full stratification of the real atmosphere and we consider only a single layer of incompressible fluid, the motions that it supports have close analogues in the real atmosphere (and ocean). 4.1 Introduction to the shallow water approximation. We consider the situation depicted in Fig. 1 where we have a single layer of incompressible fluid of uniform density ρ. The fluid above is taken to be of negligible density such that the surface is effectively free. There may be bottom topography of height hB. The free surface height is ht(x, y, t) and the mean free surface height is denoted by H. At any point the free surface height perturbation (i.e. the anomaly from the mean) is denoted ′ by h = ht H. The system is said to be shallow as the depth H is much smaller than the horizontal− scale of the fluid. A small aspect ratio of the system implies (by scale analysis of the continuity equation) that vertical velocities are much smaller than horizontal velocities. This is a condition which allows us to assume hydrostatic balance in the vertical. 4.1.1 Momentum balance in the shallow water system In the vertical we assume that hydrostatic balance holds i.e.