DOCSLIB.ORG

Generalized Displacement Maps

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Generalized Displacement Maps See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/220853059 Generalized Displacement Maps. Conference Paper · January 2004 DOI: 10.2312/EGWR/EGSR04/227-233 · Source: DBLP CITATIONS READS 77 66 6 authors, including: Xin Tong Shi-Min Hu Microsoft Tsinghua University 93 PUBLICATIONS 2,322 CITATIONS 198 PUBLICATIONS 4,662 CITATIONS SEE PROFILE SEE PROFILE Baining Guo Heung-Yeung Shum Microsoft Microsoft 166 PUBLICATIONS 5,366 CITATIONS 301 PUBLICATIONS 18,616 CITATIONS SEE PROFILE SEE PROFILE All content following this page was uploaded by Shi-Min Hu on 26 March 2014. The user has requested enhancement of the downloaded file. All in-text references underlined in blue are added to the original document and are linked to publications on ResearchGate, letting you access and read them immediately. Eurographics Symposium on Rendering (2004) H. W. Jensen, A. Keller (Editors) Generalized Displacement Maps † ∗ ∗ ∗ ∗ Xi Wang Xin Tong Stephen Lin Shimin Hu Baining Guo Heung-Yeung Shum Tsinghua University ∗ Microsoft Research Asia Abstract In this paper, we introduce a real-time algorithm to render the rich visual effects of general non-height-field geo- metric details, known as mesostructure. Our method is based on a five-dimensional generalized displacement map (GDM) that represents the distance of solid mesostructure along any ray cast from any point within a volumetric sample. With this GDM information, we propose a technique that computes mesostructure visibility jointly in ob- ject space and texture space which enables both control of texture distortion and efficient computation of texture coordinates and shadowing. GDM can be rendered with either local or global illumination as a per-pixel process in graphics hardware to achieve real-time rendering of general mesostructure. 1. Introduction Fine scale surface geometry, known as mesostructure, is an integral component in the appearance of many real-world materials and objects. The rendering of mesostructure pro- vides not only fine resolution form to a surface, but also rich visual details such as fine-scale shading, shadows, occlu- sions and silhouettes. To enhance the realism of synthesized images, much attention has been focused on efficient and comprehensive methods for rendering mesostructure and its detailed appearance features. The two most common approaches to mesostructure ren- dering are by mapping images and by mapping geome- try onto a surface. Bidirectional texture functions (BTFs) [DNvGK99] record images of a mesostructure sample under different lighting and viewing directions, but since this rep- resentation contains no 3D geometric information, silhou- ettes and the effects of surface curvature cannot be rendered. These problems can be handled by mapping mesostructure Figure 1: Mesostructure rendering with GDM. Left column: geometry onto a surface to form a detailed object model, under local illumination. Right column: under global illumi- as done with displacement maps [Coo84] and volumet- nation. ric textures [KK89, Ney98]. Although the visual effects of mesostructure can be rendered from such a model, the large amount of detailed geometry mapped into the object space ject space can be avoided by precomputing the visibility can lead to considerable processing. of mesostructure points and storing it in texture space, as proposed in view-dependent displacement mapping (VDM) The burdens of handling directly mapped geometry in ob- ∗ [WWT 03]. With this information, VDM achieves real-time rendering of mesostructure visual effects including silhou- † This work was done while Xi Wang was a visiting student at Mi- ettes. This method, however, suffers from two significant crosoft Research Asia. drawbacks. One is that it can be applied only to height-field c The Eurographics Association 2004. X. Wang, X. Tong, S. Lin, S. Hu, B. Guo & H.-Y. Shum / Generalized Displacement Maps geometry on closed surfaces. The other is that VDM can mesostructure sample, the 2D geometric structure inherent be practically precomputed for only a limited class of sur- in images precludes rendering of mesostructure silhouettes. face shapes, e.g., with respect to a single surface curvature ∗ Most prior techniques assume that mesostructures have parameter as in [WWT 03]. As a result, the precomputed the form of height fields on a mesh, a 2-1/2 D repre- VDM lacks the specificity to accurately represent surfaces sentation. For rendering mesostructures that have height with curvature variations and texture warping, which can field geometry, bump mapping [Bli78] and its exten- consequently lead to significant texture distortions. sions [Max88, SC00, BM93, HDKS00] offer an efficient ap- In this paper, we present a general mesostructure render- proach, but do not account for silhouettes. Silhouettes can be ing technique based on a proposed generalized displace- rendered by displacement maps [Coo84, CCC87], which ex- ment map (GDM), which represents the distance of solid plicitly model the geometric details of height fields. While mesostructure along any ray cast from any point within techniques based on height fields benefit from relative ease a volumetric texture. Unlike previous displacement map in processing, they lack the generality to describe a range of methods which model surfaces using one offset value per surface geometries that includes weave patterns and slanted texel, generalized displacement maps can handle arbitrary protrusions. non-height-field mesostructures. Furthermore, the GDM ap- Volumetric textures provide a general 3D representation proach overcomes both the texture distortion problems of of mesostructure as volumetric data sampled on 3D regu- VDM and the computational expense of directly mapped ge- lar grids [KK89, Ney98]. Traditionally, volumetric textures ometry by computing visibility jointly in texture space and are rendered by tracing rays through a shell volume mapped object space. The precomputed GDM values facilitate tex- on a surface, which is expensive for real time applications. ture coordinate computation of viewing rays whose piece- Recently, a set of slice-based approaches have been devel- wise linear trajectory in texture space is determined in object oped for volumetric texture rendering. Meyer et al. [MN98] space according to the shape of the base mesh. By account- rendered the volume prism extruded from each triangle as a ing for curvature variations and texture warping in object stack of axis-aligned textured slices. Lensch et al. [LDS02] space, ray intersections in texture space are more accurately used a set of slices parallel to the projection plane to ren- established, resulting in less texture distortion. der the shell volume. In [LPFH01], volumetric fur mapped The GDM can similarly be used to quickly determine on a surface is rendered as concentric layers from the skin whether the intersection point is shadowed from local illumi- outwards, and extruded fins from triangle edges near the sil- nation, and can moreover be efficiently employed for scenes houette are also rendered to reduce artifacts. Daubert et al. with global illumination. With a simple per-pixel implemen- [DS02] applied a precomputed visibility map to render shad- tation in graphics hardware, GDM can render complex volu- owing effects of thin knitwear. In these slice-based methods, metric textures including silhouettes in real time to produce the number of slices used for each triangle increases with detailed mesostructure appearance as shown in Fig. 1. The volumetric resolution. This encumbers the rendering process contributions of this work are summarized as follows: with additional overhead that is magnified when sophisti- cated per-pixel shading is incorporated. To our knowledge, • the generalized displacement map for rendering of general no previous work has been able to render volumetric textures non-height-field mesostructure on both open and closed with global illumination in real time. surfaces • visibility computation in texture and object spaces to re- Related methods for rapid software rendering include the duce texture distortion and increase efficiency work of Arvo and Kirk [AK87], which uses view-dependent • a hardware implementation of GDM for real-time render- distance data in volumes to accelerate ray tracing. Dischler ing with either local and global illumination [Dis98] used ray tracing in texture space to map mesostruc- tures onto base geometry. He also proposed a special data structure to accelerate the software rendering. Daubert et 2. Related Work ∗ al. [DKS 03] precomputed visibility information and then Previous methods for mesostructure rendering can be cate- reused it for shadow computation and indirect illumination. gorized by the dimensionality of their geometric represen- In GDM, visibility information is used for rendering both tations. Highly realistic mesostructure appearance can be silhouettes and shadows in real time. modelled from collections of 2D images such as BTFs. Poly- nomial texture maps [MGW01] represent mesostructure ap- 3. GDM Modeling and Rendering pearance of each surface point under different lighting di- rections by fitting a biquadric polynomial. For non-diffuse Our mesostructure rendering method takes mesostructure surfaces, this approach models only a fixed viewpoint. Re- geometry as input and computes its GDM. After the GDM cently, [SLSS03] integrated the BTF with precomputed radi- texture is mapped to a surface, rendering is performed by a ance transfer of macro-scale geometry, and then rendered the
Load more

Recommended publications
  • Motion Projectile Motion,And Straight Linemotion, Differences Between the Similaritiesand 2 CHAPTER 2 Acceleration Make Thefollowing As Youreadthe ●
    026_039_Ch02_RE_896315.qxd 3/23/10 5:08 PM Page 36 User-040 113:GO00492:GPS_Reading_Essentials_SE%0:XXXXXXXXXXXXX_SE:Application_File chapter 2 Motion section ●3 Acceleration What You’ll Learn Before You Read ■ how acceleration, time, and velocity are related Describe what happens to the speed of a bicycle as it goes ■ the different ways an uphill and downhill. object can accelerate ■ how to calculate acceleration ■ the similarities and differences between straight line motion, projectile motion, and circular motion Read to Learn Study Coach Outlining As you read the Velocity and Acceleration section, make an outline of the important information in A car sitting at a stoplight is not moving. When the light each paragraph. turns green, the driver presses the gas pedal and the car starts moving. The car moves faster and faster. Speed is the rate of change of position. Acceleration is the rate of change of velocity. When the velocity of an object changes, the object is accelerating. Remember that velocity is a measure that includes both speed and direction. Because of this, a change in velocity can be either a change in how fast something is moving or a change in the direction it is moving. Acceleration means that an object changes it speed, its direction, or both. How are speeding up and slowing down described? ●D Construct a Venn When you think of something accelerating, you probably Diagram Make the following trifold Foldable to compare and think of it as speeding up. But an object that is slowing down contrast the characteristics of is also accelerating. Remember that acceleration is a change in acceleration, speed, and velocity.
    [Show full text]
  • Frames of Reference
    Galilean Relativity 1 m/s 3 m/s Q. What is the women velocity? A. With respect to whom? Frames of Reference: A frame of reference is a set of coordinates (for example x, y & z axes) with respect to whom any physical quantity can be determined. Inertial Frames of Reference: - The inertia of a body is the resistance of changing its state of motion. - Uniformly moving reference frames (e.g. those considered at 'rest' or moving with constant velocity in a straight line) are called inertial reference frames. - Special relativity deals only with physics viewed from inertial reference frames. - If we can neglect the effect of the earth’s rotations, a frame of reference fixed in the earth is an inertial reference frame. Galilean Coordinate Transformations: For simplicity: - Let coordinates in both references equal at (t = 0 ). - Use Cartesian coordinate systems. t1 = t2 = 0 t1 = t2 At ( t1 = t2 ) Galilean Coordinate Transformations are: x2= x 1 − vt 1 x1= x 2+ vt 2 or y2= y 1 y1= y 2 z2= z 1 z1= z 2 Recall v is constant, differentiation of above equations gives Galilean velocity Transformations: dx dx dx dx 2 =1 − v 1 =2 − v dt 2 dt 1 dt 1 dt 2 dy dy dy dy 2 = 1 1 = 2 dt dt dt dt 2 1 1 2 dz dz dz dz 2 = 1 1 = 2 and dt2 dt 1 dt 1 dt 2 or v x1= v x 2 + v v x2 =v x1 − v and Similarly, Galilean acceleration Transformations: a2= a 1 Physics before Relativity Classical physics was developed between about 1650 and 1900 based on: * Idealized mechanical models that can be subjected to mathematical analysis and tested against observation.
    [Show full text]
  • Position, Displacement, Velocity Big Picture
    Position, Displacement, Velocity Big Picture I Want to know how/why things move I Need a way to describe motion mathematically: \Kinematics" I Tools of kinematics: calculus (rates) and vectors (directions) I Chapters 2, 4 are all about kinematics I First 1D, then 2D/3D I Main ideas: position, velocity, acceleration Language is crucial Physics uses ordinary words but assigns specific technical meanings! WORD ORDINARY USE PHYSICS USE position where something is where something is velocity speed speed and direction speed speed magnitude of velocity vec- tor displacement being moved difference in position \as the crow flies” from one instant to another Language, continued WORD ORDINARY USE PHYSICS USE total distance displacement or path length traveled path length trav- eled average velocity | displacement divided by time interval average speed total distance di- total distance divided by vided by time inter- time interval val How about some examples? Finer points I \instantaneous" velocity v(t) changes from instant to instant I graphically, it's a point on a v(t) curve or the slope of an x(t) curve I average velocity ~vavg is not a function of time I it's defined for an interval between instants (t1 ! t2, ti ! tf , t0 ! t, etc.) I graphically, it's the \rise over run" between two points on an x(t) curve I in 1D, vx can be called v I it's a component that is positive or negative I vectors don't have signs but their components do What you need to be able to do I Given starting/ending position, time, speed for one or more trip legs, calculate average
    [Show full text]
  • Chapter 3 Motion in Two and Three Dimensions
    Chapter 3 Motion in Two and Three Dimensions 3.1 The Important Stuff 3.1.1 Position In three dimensions, the location of a particle is specified by its location vector, r: r = xi + yj + zk (3.1) If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is ∆r = r1 − r2 (3.2) = (x2 − x1)i +(y2 − y1)j +(z2 − z1)k (3.3) 3.1.2 Velocity If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is ∆r ∆x ∆y ∆z v = = i + j + k (3.4) ∆t ∆t ∆t ∆t As before, a more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero. It is the time derivative of the position vector r: dr v = (3.5) dt d = (xi + yj + zk) (3.6) dt dx dy dz = i + j + k (3.7) dt dt dt can be written: v = vxi + vyj + vzk (3.8) 51 52 CHAPTER 3. MOTION IN TWO AND THREE DIMENSIONS where dx dy dz v = v = v = (3.9) x dt y dt z dt The instantaneous velocity v of a particle is always tangent to the path of the particle. 3.1.3 Acceleration If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is ∆v ∆v ∆v ∆v a = = x i + y j + z k (3.10) ∆t ∆t ∆t ∆t but a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a.
    [Show full text]
  • Exploring Robotics Joel Kammet Supplemental Notes on Gear Ratios
    CORC 3303 – Exploring Robotics Joel Kammet Supplemental notes on gear ratios, torque and speed Vocabulary SI (Système International d'Unités) – the metric system force torque axis moment arm acceleration gear ratio newton – Si unit of force meter – SI unit of distance newton-meter – SI unit of torque Torque Torque is a measure of the tendency of a force to rotate an object about some axis. A torque is meaningful only in relation to a particular axis, so we speak of the torque about the motor shaft, the torque about the axle, and so on. In order to produce torque, the force must act at some distance from the axis or pivot point. For example, a force applied at the end of a wrench handle to turn a nut around a screw located in the jaw at the other end of the wrench produces a torque about the screw. Similarly, a force applied at the circumference of a gear attached to an axle produces a torque about the axle. The perpendicular distance d from the line of force to the axis is called the moment arm. In the following diagram, the circle represents a gear of radius d. The dot in the center represents the axle (A). A force F is applied at the edge of the gear, tangentially. F d A Diagram 1 In this example, the radius of the gear is the moment arm. The force is acting along a tangent to the gear, so it is perpendicular to the radius. The amount of torque at A about the gear axle is defined as = F×d 1 We use the Greek letter Tau ( ) to represent torque.
    [Show full text]
  • Oscillations
    CHAPTER FOURTEEN OSCILLATIONS 14.1 INTRODUCTION In our daily life we come across various kinds of motions. You have already learnt about some of them, e.g., rectilinear 14.1 Introduction motion and motion of a projectile. Both these motions are 14.2 Periodic and oscillatory non-repetitive. We have also learnt about uniform circular motions motion and orbital motion of planets in the solar system. In 14.3 Simple harmonic motion these cases, the motion is repeated after a certain interval of 14.4 Simple harmonic motion time, that is, it is periodic. In your childhood, you must have and uniform circular enjoyed rocking in a cradle or swinging on a swing. Both motion these motions are repetitive in nature but different from the 14.5 Velocity and acceleration periodic motion of a planet. Here, the object moves to and fro in simple harmonic motion about a mean position. The pendulum of a wall clock executes 14.6 Force law for simple a similar motion. Examples of such periodic to and fro harmonic motion motion abound: a boat tossing up and down in a river, the 14.7 Energy in simple harmonic piston in a steam engine going back and forth, etc. Such a motion motion is termed as oscillatory motion. In this chapter we 14.8 Some systems executing study this motion. simple harmonic motion The study of oscillatory motion is basic to physics; its 14.9 Damped simple harmonic motion concepts are required for the understanding of many physical 14.10 Forced oscillations and phenomena. In musical instruments, like the sitar, the guitar resonance or the violin, we come across vibrating strings that produce pleasing sounds.
    [Show full text]
  • Rotation: Moment of Inertia and Torque
    Rotation: Moment of Inertia and Torque Every time we push a door open or tighten a bolt using a wrench, we apply a force that results in a rotational motion about a fixed axis. Through experience we learn that where the force is applied and how the force is applied is just as important as how much force is applied when we want to make something rotate. This tutorial discusses the dynamics of an object rotating about a fixed axis and introduces the concepts of torque and moment of inertia. These concepts allows us to get a better understanding of why pushing a door towards its hinges is not very a very effective way to make it open, why using a longer wrench makes it easier to loosen a tight bolt, etc. This module begins by looking at the kinetic energy of rotation and by defining a quantity known as the moment of inertia which is the rotational analog of mass. Then it proceeds to discuss the quantity called torque which is the rotational analog of force and is the physical quantity that is required to changed an object's state of rotational motion. Moment of Inertia Kinetic Energy of Rotation Consider a rigid object rotating about a fixed axis at a certain angular velocity. Since every particle in the object is moving, every particle has kinetic energy. To find the total kinetic energy related to the rotation of the body, the sum of the kinetic energy of every particle due to the rotational motion is taken. The total kinetic energy can be expressed as ..
    [Show full text]
  • Circular Motion Angular Velocity
    PHY131H1F - Class 8 Quiz time… – Angular Notation: it’s all Today, finishing off Chapter 4: Greek to me! d • Circular Motion dt • Rotation θ is an angle, and the S.I. unit of angle is rad. The time derivative of θ is ω. What are the S.I. units of ω ? A. m/s2 B. rad / s C. N/m D. rad E. rad /s2 Last day I asked at the end of class: Quiz time… – Angular Notation: it’s all • You are driving North Highway Greek to me! d 427, on the smoothly curving part that will join to the Westbound 401. v dt Your speedometer is constant at 115 km/hr. Your steering wheel is The time derivative of ω is α. not rotating, but it is turned to the a What are the S.I. units of α ? left to follow the curve of the A. m/s2 highway. Are you accelerating? B. rad / s • ANSWER: YES! Any change in velocity, either C. N/m magnitude or speed, implies you are accelerating. D. rad • If so, in what direction? E. rad /s2 • ANSWER: West. If your speed is constant, acceleration is always perpendicular to the velocity, toward the centre of circular path. Circular Motion r = constant Angular Velocity s and θ both change as the particle moves s = “arc length” θ = “angular position” when θ is measured in radians when ω is measured in rad/s 1 Special case of circular motion: Uniform Circular Motion A carnival has a Ferris wheel where some seats are located halfway between the center Tangential velocity is and the outside rim.
    [Show full text]
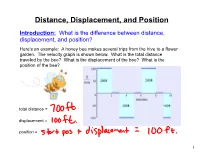
  • Distance, Displacement, and Position
    Distance, Displacement, and Position Introduction: What is the difference between distance, displacement, and position? Here's an example: A honey bee makes several trips from the hive to a flower garden. The velocity graph is shown below. What is the total distance traveled by the bee? What is the displacement of the bee? What is the position of the bee? total distance = displacement = position = 1 Warm-up A particle moves along the x-axis so that the acceleration at any time t is given by: At time , the velocity of the particle is and at time , the position is . (a) Write an expression for the velocity of the particle at any time . (b) For what values of is the particle at rest? (c) Write an expression for the position of the particle at any time . (d) Find the total distance traveled by the particle from to . 2 Warm-up Answers (a) (b) (c) (d) Total Distance = 3 Now, using the equation from the warm-up find the following (WITHOUT A CALCULATOR): (a) the total distance from 0 to 4 (b) the displacement from 0 to 4 4 To find the displacement (position shift) from the velocity function, we just integrate the function. The negative areas below the x-axis subtract from the total displacement. Displacement = To find the distance traveled we have to use absolute value. Distance traveled = To find the distance traveled by hand you must: Find the roots of the velocity equation and integrate in pieces, just like when we found the area between a curve and x-axis.
    [Show full text]
  • Torque Speed Characteristics of a Blower Load
    Torque Speed Characteristics of a Blower Load 1 Introduction The speed dynamics of a motor is given by the following equation dω J = T (ω) − T (ω) dt e L The performance of the motor is thus dependent on the torque speed characteristics of the motor and the load. The steady state operating speed (ωe) is determined by the solution of the equation Tm(ωe) = Te(ωe) Most of the loads can be classified into the following 4 general categories. 1.1 Constant torque type load A constant torque load implies that the torque required to keep the load running is the same at all speeds. A good example is a drum-type hoist, where the torque required varies with the load on the hook, but not with the speed of hoisting. Figure 1: Connection diagram 1.2 Torque proportional to speed The characteristics of the charge imply that the torque required increases with the speed. This par- ticularly applies to helical positive displacement pumps where the torque increases linearly with the speed. 1 Figure 2: Connection diagram 1.3 Torque proportional to square of the speed (fan type load) Quadratic torque is the most common load type. Typical applications are centrifugal pumps and fans. The torque is quadratically, and the power is cubically proportional to the speed. Figure 3: Connection diagram 1.4 Torque inversely proportional to speed (const power type load) A constant power load is normal when material is being rolled and the diameter changes during rolling. The power is constant and the torque is inversely proportional to the speed.
    [Show full text]
  • High-Speed Ground Transportation Noise and Vibration Impact Assessment
    High-Speed Ground Transportation U.S. Department of Noise and Vibration Impact Assessment Transportation Federal Railroad Administration Office of Railroad Policy and Development Washington, DC 20590 Final Report DOT/FRA/ORD-12/15 September 2012 NOTICE This document is disseminated under the sponsorship of the Department of Transportation in the interest of information exchange. The United States Government assumes no liability for its contents or use thereof. Any opinions, findings and conclusions, or recommendations expressed in this material do not necessarily reflect the views or policies of the United States Government, nor does mention of trade names, commercial products, or organizations imply endorsement by the United States Government. The United States Government assumes no liability for the content or use of the material contained in this document. NOTICE The United States Government does not endorse products or manufacturers. Trade or manufacturers’ names appear herein solely because they are considered essential to the objective of this report. REPORT DOCUMENTATION PAGE Form Approved OMB No. 0704-0188 Public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing this burden, to Washington Headquarters Services, Directorate for Information Operations and Reports, 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302, and to the Office of Management and Budget, Paperwork Reduction Project (0704-0188), Washington, DC 20503.
    [Show full text]
  • Frame of Reference
    Frame of Reference Ineral frame of reference– • a reference frame with a constant speed • a reference frame that is not accelerang • If frame “A” has a constant speed with respect to an ineral frame “B”, then frame “A” is also an ineral frame of reference. Newton’s 3 laws of moon are valid in an ineral frame of reference. Example: We consider the earth or the “ground” as an ineral frame of reference. Observing from an object in moon with a constant speed (a = 0) is an ineral frame of reference A non‐ineral frame of reference is one that is accelerang and Newton’s laws of moon appear invalid unless ficous forces are used to describe the moon of objects observed in the non‐ineral reference frame. Example: If you are in an automobile when the brakes are abruptly applied, then you will feel pushed toward the front of the car. You may actually have to extend you arms to prevent yourself from going forward toward the dashboard. However, there is really no force pushing you forward. The car, since it is slowing down, is an accelerang, or non‐ineral, frame of reference, and the law of inera (Newton’s 1st law) no longer holds if we use this non‐ineral frame to judge your moon. An observer outside the car however, standing on the sidewalk, will easily understand that your moon is due to your inera…you connue your path of moon unl an opposing force (contact with the dashboard) stops you. No “fake force” is needed to explain why you connue to move forward as the car stops.
    [Show full text]