Computer Certified Efficient Exact Reals In
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Role of the Interval Domain in Modern Exact Real Airthmetic
The Role of the Interval Domain in Modern Exact Real Airthmetic Andrej Bauer Iztok Kavkler Faculty of Mathematics and Physics University of Ljubljana, Slovenia Domains VIII & Computability over Continuous Data Types Novosibirsk, September 2007 Teaching theoreticians a lesson Recently I have been told by an anonymous referee that “Theoreticians do not like to be taught lessons.” and by a friend that “You should stop competing with programmers.” In defiance of this advice, I shall talk about the lessons I learned, as a theoretician, in programming exact real arithmetic. The spectrum of real number computation slow fast Formally verified, Cauchy sequences iRRAM extracted from streams of signed digits RealLib proofs floating point Moebius transformtions continued fractions Mathematica "theoretical" "practical" I Common features: I Reals are represented by successive approximations. I Approximations may be computed to any desired accuracy. I State of the art, as far as speed is concerned: I iRRAM by Norbert Muller,¨ I RealLib by Branimir Lambov. What makes iRRAM and ReaLib fast? I Reals are represented by sequences of dyadic intervals (endpoints are rationals of the form m/2k). I The approximating sequences need not be nested chains of intervals. I No guarantee on speed of converge, but arbitrarily fast convergence is possible. I Previous approximations are not stored and not reused when the next approximation is computed. I Each next approximation roughly doubles the amount of work done. The theory behind iRRAM and RealLib I Theoretical models used to design iRRAM and RealLib: I Type Two Effectivity I a version of Real RAM machines I Type I representations I The authors explicitly reject domain theory as a suitable computational model. -

Division by Fractions 6.1.1 - 6.1.4
DIVISION BY FRACTIONS 6.1.1 - 6.1.4 Division by fractions introduces three methods to help students understand how dividing by fractions works. In general, think of division for a problem like 8..,.. 2 as, "In 8, how many groups of 2 are there?" Similarly, ½ + ¼ means, "In ½ , how many fourths are there?" For more information, see the Math Notes boxes in Lessons 7.2 .2 and 7 .2 .4 of the Core Connections, Course 1 text. For additional examples and practice, see the Core Connections, Course 1 Checkpoint 8B materials. The first two examples show how to divide fractions using a diagram. Example 1 Use the rectangular model to divide: ½ + ¼ . Step 1: Using the rectangle, we first divide it into 2 equal pieces. Each piece represents ½. Shade ½ of it. - Step 2: Then divide the original rectangle into four equal pieces. Each section represents ¼ . In the shaded section, ½ , there are 2 fourths. 2 Step 3: Write the equation. Example 2 In ¾ , how many ½ s are there? In ¾ there is one full ½ 2 2 I shaded and half of another Thatis,¾+½=? one (that is half of one half). ]_ ..,_ .l 1 .l So. 4 . 2 = 2 Start with ¾ . 3 4 (one and one-half halves) Parent Guide with Extra Practice © 2011, 2013 CPM Educational Program. All rights reserved. 49 Problems Use the rectangular model to divide. .l ...:... J_ 1 ...:... .l 1. ..,_ l 1 . 1 3 . 6 2. 3. 4. 1 4 . 2 5. 2 3 . 9 Answers l. 8 2. 2 3. 4 one thirds rm I I halves - ~I sixths fourths fourths ~I 11 ~'.¿;¡~:;¿~ ffk] 8 sixths 2 three fourths 4. -
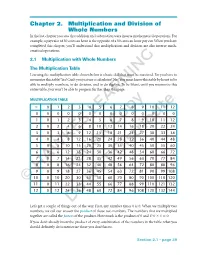
Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers. -

Fast Integer Division – a Differentiated Offering from C2000 Product Family
Application Report SPRACN6–July 2019 Fast Integer Division – A Differentiated Offering From C2000™ Product Family Prasanth Viswanathan Pillai, Himanshu Chaudhary, Aravindhan Karuppiah, Alex Tessarolo ABSTRACT This application report provides an overview of the different division and modulo (remainder) functions and its associated properties. Later, the document describes how the different division functions can be implemented using the C28x ISA and intrinsics supported by the compiler. Contents 1 Introduction ................................................................................................................... 2 2 Different Division Functions ................................................................................................ 2 3 Intrinsic Support Through TI C2000 Compiler ........................................................................... 4 4 Cycle Count................................................................................................................... 6 5 Summary...................................................................................................................... 6 6 References ................................................................................................................... 6 List of Figures 1 Truncated Division Function................................................................................................ 2 2 Floored Division Function................................................................................................... 3 3 Euclidean -

Multiplication and Divisions
Third Grade Math nd 2 Grading Period Power Objectives: Academic Vocabulary: multiplication array Represent and solve problems involving multiplication and divisor commutative division. (P.O. #1) property Understand properties of multiplication and the distributive property relationship between multiplication and divisions. estimation division factor column (P.O. #2) Multiply and divide with 100. (P.O. #3) repeated addition multiple Solve problems involving the four operations, and identify associative property quotient and explain the patterns in arithmetic. (P.O. #4) rounding row product equation Multiplication and Division Enduring Understandings: Essential Questions: Mathematical operations are used in solving problems In what ways can operations affect numbers? in which a new value is produced from one or more How can different strategies be helpful when solving a values. problem? Algebraic thinking involves choosing, combining, and How does knowing and using algorithms help us to be applying effective strategies for answering questions. Numbers enable us to use the four operations to efficient problem solvers? combine and separate quantities. How are multiplication and addition alike? See below for additional enduring understandings. How are subtraction and division related? See below for additional essential questions. Enduring Understandings: Multiplication is repeated addition, related to division, and can be used to solve story problems. For a given set of numbers, there are relationships that -

AUTHOR Multiplication and Division. Mathematics-Methods
DOCUMENT RESUME ED 221 338 SE 035 008, AUTHOR ,LeBlanc, John F.; And Others TITLE Multiplication and Division. Mathematics-Methods 12rogram Unipt. INSTITUTION Indiana ,Univ., Bloomington. Mathematics Education !Development Center. , SPONS AGENCY ,National Science Foundation, Washington, D.C. REPORT NO :ISBN-0-201-14610-x PUB DATE 76 . GRANT. NSF-GY-9293 i 153p.; For related documents, see SE 035 006-018. NOTE . ,. EDRS PRICE 'MF01 Plus Postage. PC Not Available from EDRS. DESCRIPTORS iAlgorithms; College Mathematics; *Division; Elementary Education; *Elementary School Mathematics; 'Elementary School Teachers; Higher Education; 'Instructional1 Materials; Learning Activities; :*Mathematics Instruction; *Multiplication; *Preservice Teacher Education; Problem Solving; :Supplementary Reading Materials; Textbooks; ;Undergraduate Study; Workbooks IDENTIFIERS i*Mathematics Methods Program ABSTRACT This unit is 1 of 12 developed for the university classroom portign_of the Mathematics-Methods Program(MMP), created by the Indiana pniversity Mathematics EducationDevelopment Center (MEDC) as an innovative program for the mathematics training of prospective elenientary school teachers (PSTs). Each unit iswritten in an activity format that involves the PST in doing mathematicswith an eye towardaiplication of that mathematics in the elementary school. This do ument is one of four units that are devoted tothe basic number wo k in the elementary school. In addition to an introduction to the unit, the text has sections on the conceptual development of nultiplication -

Understanding the Concept of Division
Understanding the Concept of Division ________________ An Honors thesis presented to the faculty of the Department of Mathematics East Tennessee State University In partial fulfillment of the requirements for the Honors-in-Discipline Program for a Bachelor of Science in Mathematics ________________ By Leanna Horton May, 2007 ________________ George Poole, Ph.D. Advisor approval: ___________________________ ABSTRACT Understanding the Concept of Division by Leanna Horton The purpose of this study was to assess how well elementary students and mathematics educators understand the concept of division. Participants included 210 fourth and fifth grade students, 17 elementary math teachers, and seven collegiate level math faculty. The problems were designed to assess whether or not participants understood when a solution would include a remainder and if they could accurately explain their responses, including giving appropriate units to all numbers in their solution. The responses given by all participants and the methods used by the elementary students were analyzed. The results indicate that a significant number of the student participants had difficulties giving complete, accurate explanations to some of the problems. The results also indicate that both the elementary students and teachers had difficulties understanding when a solution will include a remainder and when it will include a fraction. The analysis of the methods used indicated that the use of long division or pictures produced the most accurate solutions. 2 CONTENTS Page ABSTRACT………………………………………………………………………… 2 LIST OF TABLES………………………………………………………………….. 6 LIST OF FIGURES………………………………………………………………… 7 1 Introduction…………………………………………………………………. 8 Purpose……………………………………………………………… 8 Literature Review…………………………………………………… 9 Teachers..…………………………………………………….. 9 Students…………………………………………………….. 10 Math and Gender……………………………………………. 13 Word Problems……………………………………………………… 14 Number of Variables……………………………………….. 15 Types of Variables…………………………………………. -

Interpreting Multiplication and Division
CONCEPT DEVELOPMENT Mathematics Assessment Project CLASSROOM CHALLENGES A Formative Assessment Lesson Interpreting Multiplication and Division Mathematics Assessment Resource Service University of Nottingham & UC Berkeley For more details, visit: http://map.mathshell.org © 2015 MARS, Shell Center, University of Nottingham May be reproduced, unmodified, for non-commercial purposes under the Creative Commons license detailed at http://creativecommons.org/licenses/by-nc-nd/3.0/ - all other rights reserved Interpreting Multiplication and Division MATHEMATICAL GOALS This lesson unit is designed to help students to interpret the meaning of multiplication and division. Many students have a very limited understanding of these operations and only recognise them in terms of ‘times’ and ‘share’. They find it hard to give any meaning to calculations that involve non- integers. This is one reason why they have difficulty when choosing the correct operation to perform when solving word problems. COMMON CORE STATE STANDARDS This lesson relates to the following Standards for Mathematical Content in the Common Core State Standards for Mathematics: 6.NS: Apply and extend previous understandings of multiplication and division to divide fractions by fractions. This lesson also relates to the following Standards for Mathematical Practice in the Common Core State Standards for Mathematics, with a particular emphasis on Practices 1, 2, 3, 5, and 6: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. INTRODUCTION The unit is structured in the following way: • Before the lesson, students work individually on a task designed to reveal their current levels of understanding. -

Solve 87 ÷ 5 by Using an Area Model. Use Long Division and the Distributive Property to Record Your Work. Lessons 14 Through 21
GRADE 4 | MODULE 3 | TOPIC E | LESSONS 14–21 KEY CONCEPT OVERVIEW Lessons 14 through 21 focus on division. Students develop an understanding of remainders. They use different methods to solve division problems. You can expect to see homework that asks your child to do the following: ▪ Use the RDW process to solve word problems involving remainders. ▪ Show division by using place value disks, arrays, area models, and long division. ▪ Check division answers by using multiplication and addition. SAMPLE PROBLEM (From Lesson 21) Solve 87 ÷ 5 by using an area model. Use long division and the distributive property to record your work. ()40 ÷+54()05÷+()55÷ =+88+1 =17 ()51×+72= 87 Additional sample problems with detailed answer steps are found in the Eureka Math Homework Helpers books. Learn more at GreatMinds.org. For more resources, visit » Eureka.support GRADE 4 | MODULE 3 | TOPIC E | LESSONS 14–21 HOW YOU CAN HELP AT HOME ▪ Provide your child with many opportunities to interpret remainders. For example, give scenarios such as the following: Arielle wants to buy juice boxes for her classmates. The juice boxes come in packages of 6. If there are 19 students in Arielle’s class, how many packages of juice boxes will she need to buy? (4) Will there be any juice boxes left? (Yes) How many? (5) ▪ Play a game of Remainder or No Remainder with your child. 1. Say a division expression like 11 ÷ 5. 2. Prompt your child to respond with “Remainder!” or “No remainder!” 3. Continue with a sequence such as 9 ÷ 3 (No remainder!), 10 ÷ 3 (Remainder!), 25 ÷ 3 (Remainder!), 24 ÷ 3 (No remainder!), and 37 ÷ 5 (Remainder!). -

Euclidean Algorithm and Multiplicative Inverses
Fall 2019 Chris Christensen MAT/CSC 483 Finding Multiplicative Inverses Modulo n Two unequal numbers being set out, and the less begin continually subtracted in turn from the greater, if the number which is left never measures the one before it until an unit is left, the original numbers will be prime to one another. Euclid, The Elements, Book VII, Proposition 1, c. 300 BCE. It is not necessary to do trial and error to determine the multiplicative inverse of an integer modulo n. If the modulus being used is small (like 26) there are only a few possibilities to check (26); trial and error might be a good choice. However, some modern public key cryptosystems use very large moduli and require the determination of inverses. We will now examine a method (that is due to Euclid [c. 325 – 265 BCE]) that can be used to construct multiplicative inverses modulo n (when they exist). Euclid's Elements, in addition to geometry, contains a great deal of number theory – properties of the positive integers. The Euclidean algorithm is Propositions I - II of Book VII of Euclid’s Elements (and Propositions II – III of Book X). Euclid describes a process for determining the greatest common divisor (gcd) of two positive integers. 1 The Euclidean Algorithm to Find the Greatest Common Divisor Let us begin with the two positive integers, say, 13566 and 35742. Divide the smaller into the larger: 35742=×+ 2 13566 8610 Divide the remainder (8610) into the previous divisor (35742): 13566=×+ 1 8610 4956 Continue to divide remainders into previous divisors: 8610=×+ 1 4956 3654 4956=×+ 1 3654 1302 3654=×+ 2 1302 1050 1302=×+ 1 1050 252 1050=×+ 4 252 42 252= 6 × 42 The process stops when the remainder is 0. -

Least Common Multiple (Lcm)
LEAST COMMON MULTIPLE (LCM) Use one of these two methods to find the LCM of two or more numbers. Method I: Individual Prime Factoring Method 1. Find the prime factorization of each Example: Find the LCM of 40 and 60. number in the group. 60 40 2. Make a list of ALL factors, raised to the HIGHEST power that appears in 6 10 4 10 any factorization. 2 3 2 5 2 2 3. Multiply out. 2 5 2 3 2 2 3 5 = 2 3 2 2 2 5 = 2 5 5 Make a list of ALL of the prime factors: 2, 3 & 5. Raise each factor to the highest power that appears on either list and multiply the complete list of factors: LCM = 23 3 5 = 120. Method II: Group-Factoring Method 1. Using prime numbers as divisors, Example: Find the LCM of 40 and 60. divide each number in the group, if possible. When a number is not divisible by the prime divisor just 2 ) 60 40 bring it down to the next row along 2 ) 30 20 with the quotients from the other 2 ) 15 10 divisions. Continue dividing by 3 ) 15 5 prime divisors until all quotients are ones. 5 ) 5 5 1 1 2. Multiply all of the prime divisors – the product is the LCM. LCM = 23 3 5 = 120 Remember: A Least Common Denominator (LCD) is nothing more than the LCM of the denominators of a group of fractions. Use the same steps listed above to find an LCD. LCDs are required for addition and subtraction of fractions and not required for multiplication and division. -

Massachusetts Mathematics Curriculum Framework — 2017
Massachusetts Curriculum MATHEMATICS Framework – 2017 Grades Pre-Kindergarten to 12 i This document was prepared by the Massachusetts Department of Elementary and Secondary Education Board of Elementary and Secondary Education Members Mr. Paul Sagan, Chair, Cambridge Mr. Michael Moriarty, Holyoke Mr. James Morton, Vice Chair, Boston Dr. Pendred Noyce, Boston Ms. Katherine Craven, Brookline Mr. James Peyser, Secretary of Education, Milton Dr. Edward Doherty, Hyde Park Ms. Mary Ann Stewart, Lexington Dr. Roland Fryer, Cambridge Mr. Nathan Moore, Chair, Student Advisory Council, Ms. Margaret McKenna, Boston Scituate Mitchell D. Chester, Ed.D., Commissioner and Secretary to the Board The Massachusetts Department of Elementary and Secondary Education, an affirmative action employer, is committed to ensuring that all of its programs and facilities are accessible to all members of the public. We do not discriminate on the basis of age, color, disability, national origin, race, religion, sex, or sexual orientation. Inquiries regarding the Department’s compliance with Title IX and other civil rights laws may be directed to the Human Resources Director, 75 Pleasant St., Malden, MA, 02148, 781-338-6105. © 2017 Massachusetts Department of Elementary and Secondary Education. Permission is hereby granted to copy any or all parts of this document for non-commercial educational purposes. Please credit the “Massachusetts Department of Elementary and Secondary Education.” Massachusetts Department of Elementary and Secondary Education 75 Pleasant Street, Malden, MA 02148-4906 Phone 781-338-3000 TTY: N.E.T. Relay 800-439-2370 www.doe.mass.edu Massachusetts Department of Elementary and Secondary Education 75 Pleasant Street, Malden, Massachusetts 02148-4906 Dear Colleagues, I am pleased to present to you the Massachusetts Curriculum Framework for Mathematics adopted by the Board of Elementary and Secondary Education in March 2017.