Market Sentiments Distribution Law
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Tradescript.Pdf
Service Disclaimer This manual was written for use with the TradeScript™ language. This manual and the product described in it are copyrighted, with all rights reserved. This manual and the TradeScript™ outputs (charts, images, data, market quotes, and other features belonging to the product) may not be copied, except as otherwise provided in your license or as expressly permitted in writing by Modulus Financial Engineering, Inc. Export of this technology may be controlled by the United States Government. Diversion contrary to U.S. law prohibited. Copyright © 2006 by Modulus Financial Engineering, Inc. All rights reserved. Modulus Financial Engineering and TradeScript™ are registered trademarks of Modulus Financial Engineering, Inc. in the United States and other countries. All other trademarks and service marks are the property of their respective owners. Use of the TradeScript™ product and other services accompanying your license and its documentation are governed by the terms set forth in your license. Such use is at your sole risk. The service and its documentation (including this manual) are provided "AS IS" and without warranty of any kind and Modulus Financial Engineering, Inc. AND ITS LICENSORS (HEREINAFTER COLLECTIVELY REFERRED TO AS “MFE”) EXPRESSLY DISCLAIM ALL WARRANTIES, EXPRESS OR IMPLIED, INCLUDING, BUT NOT LIMITED TO THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE AND AGAINST INFRINGEMENT. MFE DOES NOT WARRANT THAT THE FUNCTIONS CONTAINED IN THE SERVICE WILL MEET YOUR REQUIREMENTS, OR THAT THE OPERATION OF THE SERVICE WILL BE UNINTERRUPTED OR ERROR-FREE, OR THAT DEFECTS IN THE SERVICE OR ERRORS IN THE DATA WILL BE CORRECTED. FURTHERMORE, MFE DOES NOT WARRANT OR MAKE ANY REPRESENTATIONS REGARDING THE USE OR THE RESULTS OF THE USE OF THE SERVICE OR ITS DOCUMENTATION IN TERMS OF THEIR CORRECTNESS, ACCURACY, RELIABILITY, OR OTHERWISE. -
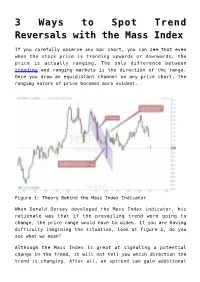
3 Ways to Spot Trend Reversals with the Mass Index
3 Ways to Spot Trend Reversals with the Mass Index If you carefully observe any bar chart, you can see that even when the stock price is trending upwards or downwards, the price is actually ranging. The only difference between trending and ranging markets is the direction of the range. Once you draw an equidistant channel on any price chart, the ranging nature of price becomes more evident. Figure 1: Theory Behind the Mass Index Indicator When Donald Dorsey developed the Mass Index indicator, his rationale was that if the prevailing trend were going to change, the price range would have to widen. If you are having difficulty imagining the situation, look at figure 1, do you see what we mean? Although the Mass Index is great at signaling a potential change in the trend, it will not tell you which direction the trend is changing. After all, an uptrend can gain additional bullish momentum and that will also help make the range much wider. You have to remember that when the Mass Index technical indicator line is going up, the climbing line is only signaling that the volatility of the stock is going up. However, the Mass Index indicator line does not signify any directional bias of the stock. That’s why you need to incorporate other technical analysis tools into your mass index trading strategies in order to identify the change of direction of the prevailing trend. Consider an analogy for a moment, you are driving a car and the mass index calculator, which shows volatility of the stock, is your speedometer. -

Data Visualization and Analysis
HTML5 Financial Charts Data visualization and analysis Xinfinit’s advanced HTML5 charting tool is also available separately from the managed data container and can be licensed for use with other tools and used in conjunction with any editor. It includes a comprehensive library of over sixty technical indictors, additional ones can easily be developed and added on request. 2 Features Analysis Tools Trading from Chart Trend Channel Drawing Instrument Selection Circle Drawing Chart Duration Rectangle Drawing Chart Intervals Fibonacci Patterns Chart Styles (Line, OHLC etc.) Andrew’s Pitchfork Comparison Regression Line and Channel Percentage (Y-axis) Up and Down arrows Log (Y-axis) Text box Show Volume Save Template Show Data values Load Template Show Last Value Save Show Cross Hair Load Show Cross Hair with Last Show Min / Max Show / Hide History panel Show Previous Close Technical Indicators Show News Flags Zooming Data Streaming Full Screen Print Select Tool Horizontal Divider Trend tool Volume by Price Horizonal Line Drawing Book Volumes 3 Features Technical Indicators Acceleration/Deceleration Oscillator Elliot Wave Oscillator Accumulation Distribution Line Envelopes Aroon Oscilltor Fast Stochastic Oscillator Aroon Up/Down Full Stochastic Oscillator Average Directional Index GMMA Average True Range GMMA Oscillator Awesome Oscillator Highest High Bearish Engulfing Historical Volatility Bollinger Band Width Ichimoku Kinko Hyo Bollinger Bands Keltner Indicator Bullish Engulfing Know Sure Thing Chaikin Money Flow Lowest Low Chaikin Oscillator -

View User Guide
Connect User Guide July 2020 [CONFIDENTIAL] Overview ................................................................................................................. 2 Logging In ............................................................................................................... 3 Menu Bar ................................................................................................................. 4 File………….. .................................................................................................................. 4 Preferences ..................................................................................................................... 6 Connect Utils ................................................................................................................... 9 Help... ............................................................................................................................ 17 Regions Menu ....................................................................................................... 18 Pages ..................................................................................................................... 20 Pages Right Click .......................................................................................................... 21 Widget Tabs .......................................................................................................... 21 Widget Tabs Right Click ............................................................................................... -

Stock Selection Strategy of A-Share Market Based on Rotation Effect And
AIMS Mathematics, 5(5): 4563–4580. DOI: 10.3934/math.2020293 Received: 09 January 2020 Accepted: 30 April 2020 http://www.aimspress.com/journal/Math Published: 22 May 2020 Research article Stock selection strategy of A-share market based on rotation effect and random forest Shuai Wang1, Zhongyan Li2;∗, Jinyun Zhu2, Zhicen Lin2 and Meiru Zhong1 1 Department of Finance, Guangdong University of Finance and Economics, Guangzhou City, Guangdong Province, China 2 Department of statistics and mathematics, Guangdong University of Finance and Economics, Guangzhou City, Guangdong Province, China * Correspondence: Email: [email protected]; Tel: +136313391161. Abstract: Due to the random nature of stock market, it is extremely difficult to capture market trends with traditional subjective analysis. Besides, the modeling and forecasting of quantitative investment strategies are not easy. Based on the research of experts and scholars at home and abroad and the rotation effect of large and small styles in China’s A-share market, a stock picking strategy combining wheeling effect and random forest is proposed. Firstly, judge the style trend of the A-share market, that is, the relatively strong style in the large and small-sized market. The strategy first judges the trend of the A-share market style, then uses a multi-factor stock selection model through random forest to select stocks among the constituent stocks of the dominant style index, and buys the selected stocks according to the optimal portfolio weights determined by the principle of minimum variance. The empirical results show that the annualized rate of return of the strategy in the eight years from January 1, 2012 to April 1, 2020 is 3.6% higher than that of the single-round strategy, far exceeding the performance of the CSI 300 Index during the same period. -

Renato Di Lorenzo Basic Technical Analysis of Financial Markets A
Renato Di Lorenzo Basic Technical Analysis of Financial Markets A Modern Approach Springer Contents Part I 1 Graphical Representation 3 1.1 Zig-Zag 3 1.2 Bar Charts 7 1.3 Candles 9 1.4 Candlevolume 9 1.5 Equivolume 11 1.6 Point and Figure 13 1.7 Kagi 16 1.8 Renko 18 1.9 Three Line Break 20 1.10 Range Bars 21 1.11 HeikinAshi 22 1.12 Validation 24 1.13 The Scales 28 1.14 TypeofPrice 30 2 Trend Analysis 33 2.1 Linear Trends 33 2.2 Cuts 38 3 Targets 43 3.1 Fibonacci Numbers 43 3.1.1 Sam Numbers 47 4 Filtering 51 4.1 SMA 51 4.2 Optimization 55 4.2.1 Buy/Sell Instructions 55 4.2.2 Date: For Example from 8.8.2010 to 8.8.2011 56 4.2.3 Initial Capital: Say 200.000 EUR or USD Depending on the Market Traded 57 XV xvj Contents 4.2.4 Commissions 57 4.2.5 Maximum Total Commitment: 100 % 57 4.2.6 Maximum Total Commitment Per Transaction: 100 % 57 4.2.7 Minimum Total Commitment Per Transaction: 1 % 57 4.2.8 Profits Reinvestment 57 4.2.9 Round Off the Number of Securities and Contracts to the Next Higher Whole Number 58 4.2.10 The Simplest Trading System 58 4.2.11 Optimization 61 4.3 EMA 66 4.4 Other Moving Averages 69 4.5 WMA and WMAS 70 4.6 RMA 75 5 Oscillation Periods 79 5.1 A Measure via RMA 79 6 Stop Loss 83 6.1 The 5 % System 83 7 Advanced Moving Averages 85 7.1 Dema and Tema 85 7.2 Zero Lag 89 7.3 Adaptive Moving Averages 92 8 Bands and Bundles 99 8.1 Bollinger Bands 99 8.2 B&CB 102 8.3 Envelops 104 8.4 Bundles 107 8.5 Guppy Bands 109 9 Other Indicators Superimposed on the Price 111 9.1 Parabolic Sar 111 9.2 Chande Kroll Stop 112 9.3 Ichimoku 116 -

Smartchart Documentation
SmartChart V1.6 Copyright (C) 2004 - 2008 Trading-Tools.com mailto:[email protected] User manual Table of Contents Table of Contents.............................................................................. 2 Welcome ......................................................................................... 4 Main Window.................................................................................... 5 Plotting an ASCII File ........................................................................ 6 Plotting a Microsoft Access (*.mdb) File............................................... 8 Preferences Dialog ............................................................................ 9 Price Plots...................................................................................... 13 Introduction................................................................................. 13 Modifying a Price Plot.................................................................... 13 Indicators ...................................................................................... 15 What is an Indicator? .................................................................... 15 Adding an Indicator ...................................................................... 15 Deleting an Indicator .................................................................... 16 Supported Indicators .................................................................... 16 Accumulation Swing Index .......................................................... 16 Aroon -
Momentum 124 Momentum (Finance) 124 Relative Strength Index 125 Stochastic Oscillator 128 Williams %R 131
PATTERNS Technical Analysis Contents Articles Technical analysis 1 CONCEPTS 11 Support and resistance 11 Trend line (technical analysis) 15 Breakout (technical analysis) 16 Market trend 16 Dead cat bounce 21 Elliott wave principle 22 Fibonacci retracement 29 Pivot point 31 Dow Theory 34 CHARTS 37 Candlestick chart 37 Open-high-low-close chart 39 Line chart 40 Point and figure chart 42 Kagi chart 45 PATTERNS: Chart Pattern 47 Chart pattern 47 Head and shoulders (chart pattern) 48 Cup and handle 50 Double top and double bottom 51 Triple top and triple bottom 52 Broadening top 54 Price channels 55 Wedge pattern 56 Triangle (chart pattern) 58 Flag and pennant patterns 60 The Island Reversal 63 Gap (chart pattern) 64 PATTERNS: Candlestick pattern 68 Candlestick pattern 68 Doji 89 Hammer (candlestick pattern) 92 Hanging man (candlestick pattern) 93 Inverted hammer 94 Shooting star (candlestick pattern) 94 Marubozu 95 Spinning top (candlestick pattern) 96 Three white soldiers 97 Three Black Crows 98 Morning star (candlestick pattern) 99 Hikkake Pattern 100 INDICATORS: Trend 102 Average Directional Index 102 Ichimoku Kinkō Hyō 103 MACD 104 Mass index 108 Moving average 109 Parabolic SAR 115 Trix (technical analysis) 116 Vortex Indicator 118 Know Sure Thing (KST) Oscillator 121 INDICATORS: Momentum 124 Momentum (finance) 124 Relative Strength Index 125 Stochastic oscillator 128 Williams %R 131 INDICATORS: Volume 132 Volume (finance) 132 Accumulation/distribution index 133 Money Flow Index 134 On-balance volume 135 Volume Price Trend 136 Force -

AN INTEGRATED STOCK MARKET FORECASTING MODEL USING NEURAL NETWORKS a Thesis Presented to the Faculty of the Fritz J. and Dolores
AN INTEGRATED STOCK MARKET FORECASTING MODEL USING NEURAL NETWORKS A thesis presented to the faculty of the Fritz J. and Dolores H. Russ College of Engineering and Technology of Ohio University In partial fulfillment of the requirements for the degree Master of Science Sriram Lakshminarayanan August 2005 © 2005 Sriram Lakshminarayanan All Rights Reserved This thesis entitled AN INTEGRATED STOCK MARKET FORECASTING MODEL USING NEURAL NETWORKS By Sriram Lakshminarayanan has been approved for the Department of Industrial and Manufacturing Systems Engineering and the Russ College of Engineering and Technology by Gary R. Weckman Associate Professor of Industrial & Manufacturing Systems Engineering Dennis Irwin Dean, Fritz J. and Dolores H. Russ College of Engineering and Technology LAKSHMINARAYANAN SRIRAM. M.S. August 2005. Industrial and Manufacturing Systems Engineering An Integrated Stock Market Forecasting Model Using Neural Networks (126pp.) Director of Thesis: Gary Weckman This thesis focuses on the development of a stock market forecasting model based on an Artificial Neural Network architecture. This study constructs a hybrid model utilizing various technical indicators, Elliott’s wave theory, sensitivity analysis and fuzzy logic. Initially, a baseline network is constructed based on available literature. The baseline model is then improved by applying several useful information domains to the different models. Optimizations of the Neural Network models are performed by augmenting the network with useful information at every stage. -

Download the Stockfetcher User Guide
TECHNICAL STOCK SCREENING AND ANALYSIS USING STOCKFETCHER User Guide and Reference Manual (Release 2.0) StockFetcher Usage Guide Table of Contents Page PREFACE ........................................................................................................VI What’s Inside ................................................................................................................ vii Document Conventions................................................................................................. vii Comments and Suggestions .........................................................................................viii CHAPTER 1. SCREENING ON STOCKFETCHER ............................................... 1 Description through Implementation .............................................................................. 2 Convenience vs. Control................................................................................................. 2 Verify Syntax.................................................................................................................. 3 Trading Stocks ................................................................................................................ 3 Basic Elements of a StockFetcher Screen....................................................................... 3 Building Your First Screen ............................................................................................. 4 CHAPTER 2. ACTIONS .................................................................................... -

VOLATILITY Displaceaverages Willians ELRBEAR Annvolatility
Indicator´s catalog AVERAGES DMKOsc AvSimpleOscP PivotUp AvAdapted DPO AvTriangularOsc PVTPOINT01 AvExponencial MACD AvTriangularOscP PVTPOINT02 AvFastk Momentum AvWeigthedOsc AvFlat MomentumSlow AvWeigthedOscP SPREAD AvL Sie1 PriceOsc AvWilderOsc BOP AvLSie2 PriceROC AvWilderOscP CorrelationIndex AvLSie3 REI BollingerBandsOsc DisagreeSpread AvQuick RSI BollingerBandsOscP DisagreeSpreadSour AvSimple SSI CCI03 MomentumSpreadOsc AvTriangular Stochastic DEMADSIF PercentSpread AvWeighted StandardDev DEMAIND PercentSpreadSour AvWilder StandardDevP DHZ Rsc SwingIndex DSS SpreadOsc BollingerBands SwingIndexAcum DYN BP Trix ELR VOLATILITY DisplaceAverages Willians ELRBEAR AnnVolatility DMAIND WilliansAD ELRBULL AvTrueRange - ATR Keltner EXPMOVAVGBOP AvTrueRangeP - ATR % Parabolic OVER AVERAGES FASTK Base RainbowChart AvAdaptedOsc FORCEINDEX BollVolatility SWMA avAdaptedOscP IDM BollVolatilityOsc T3TillsonInd AvDisagreeOsc MACDHEMEL ClosesDSi - DSiCloses TEMAIND AvDisagreeOscP MDEMASMT CG TS TFS Line AvExponentialOsc PSSTOCHRSI FDI TSF AvExponentialOscP REPULSE GapTrading WeightClose avFlatOsc SKYINDICATORC INVOSC ZigZag AvFlatOscP TFSMBO MasSindex AvLSie1Osc TII PriceEvolution CLASSICS AvLSie1OscP TTRENDTRACKIND RLA ADX AvLSie2Osc RainbowChartOsc RSL ADXR AvLSie2OscP RVI CCI AvLSie3Osc PIVOTS SNRI C SI AvLSie3OscP AroonUpDown TCF DirectionalMov AvQuickOsc CafeDerdPvotSind1 TDVLT DINegative AvQuickOscP Fibrange Tickschart DIPoSitive AvSimpleOsc PivotDown TTFIndicator INDICATORS CATALOG | VISUALCHART 2 VOLATILITY UlcerIndex VHF VolatilityChakin -
Technical Analysis from a to Z
Introduction, Trends - Technical Analysis from A to Z MetaStock Family Products Customer Corner Partners TA Training Online Charting TAAZ Book DownLoader Hot Stocks Contents Preface Technical Analysis from A to Z Acknowledgments Terminology By Steven B. Achelis To Learn More Introduction ● Technical Analysis ● Price fields ● Charts ● Support & resistance INTRODUCTION - Trends ● Trends ● Moving averages Trends ● Indicators ● Market indicators In the preceding section, we saw how support and resistance levels can be ● Line studies penetrated by a change in investor expectations (which results in shifts of the supply/demand lines). This type of a change is often abrupt and "news based." ● Periodicity ● The time element In this section, we'll review "trends." A trend represents a consistent change in prices (i.e., a change in investor expectations). Trends differ from ● Conclusion support/resistance levels in that trends represent change, whereas ● Order the Book support/resistance levels represent barriers to change. ● Learn more about Technical Analysis As shown in Figure 19, a rising trend is defined by successively higher low-prices. A rising trend can be thought of as a rising support level--the bulls are in control and are pushing prices higher. Reference Absolute Breadth Index Accumulation/Distribution Figure 19 Accumulation Swing Index Advance/Decline Line Advance/Decline Ratio Advancing-Declining Issues Advancing, Declining, Unchanged Volume Andrews' Pitchfork Arms Index Average True Range Bollinger Bands Breadth Thrust Bull/Bear Ratio Candlesticks, Japanese CANSLIM Chaikin Oscillator Commodity Channel Index Commodity Selection Index Correlation Analysis Cumulative Volume Index Cycles Demand Index Detrended Price Oscillator Directional Movement Dow Theory Ease of Movement Figure 20 shows a falling trend.