Uwaterloo Latex Thesis Template
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ma/CS 6B Class 8: Planar and Plane Graphs
1/26/2017 Ma/CS 6b Class 8: Planar and Plane Graphs By Adam Sheffer The Utilities Problem Problem. There are three houses on a plane. Each needs to be connected to the gas, water, and electricity companies. ◦ Is there a way to make all nine connections without any of the lines crossing each other? ◦ Using a third dimension or sending connections through a company or house is not allowed. 1 1/26/2017 Rephrasing as a Graph How can we rephrase the utilities problem as a graph problem? ◦ Can we draw 퐾3,3 without intersecting edges. Closed Curves A simple closed curve (or a Jordan curve) is a curve that does not cross itself and separates the plane into two regions: the “inside” and the “outside”. 2 1/26/2017 Drawing 퐾3,3 with no Crossings We try to draw 퐾3,3 with no crossings ◦ 퐾3,3 contains a cycle of length six, and it must be drawn as a simple closed curve 퐶. ◦ Each of the remaining three edges is either fully on the inside or fully on the outside of 퐶. 퐾3,3 퐶 No 퐾3,3 Drawing Exists We can only add one red-blue edge inside of 퐶 without crossings. Similarly, we can only add one red-blue edge outside of 퐶 without crossings. Since we need to add three edges, it is impossible to draw 퐾3,3 with no crossings. 퐶 3 1/26/2017 Drawing 퐾4 with no Crossings Can we draw 퐾4 with no crossings? ◦ Yes! Drawing 퐾5 with no Crossings Can we draw 퐾5 with no crossings? ◦ 퐾5 contains a cycle of length five, and it must be drawn as a simple closed curve 퐶. -

Planarity and Duality of Finite and Infinite Graphs
JOURNAL OF COMBINATORIAL THEORY, Series B 29, 244-271 (1980) Planarity and Duality of Finite and Infinite Graphs CARSTEN THOMASSEN Matematisk Institut, Universitets Parken, 8000 Aarhus C, Denmark Communicated by the Editors Received September 17, 1979 We present a short proof of the following theorems simultaneously: Kuratowski’s theorem, Fary’s theorem, and the theorem of Tutte that every 3-connected planar graph has a convex representation. We stress the importance of Kuratowski’s theorem by showing how it implies a result of Tutte on planar representations with prescribed vertices on the same facial cycle as well as the planarity criteria of Whit- ney, MacLane, Tutte, and Fournier (in the case of Whitney’s theorem and MacLane’s theorem this has already been done by Tutte). In connection with Tutte’s planarity criterion in terms of non-separating cycles we give a short proof of the result of Tutte that the induced non-separating cycles in a 3-connected graph generate the cycle space. We consider each of the above-mentioned planarity criteria for infinite graphs. Specifically, we prove that Tutte’s condition in terms of overlap graphs is equivalent to Kuratowski’s condition, we characterize completely the infinite graphs satisfying MacLane’s condition and we prove that the 3- connected locally finite ones have convex representations. We investigate when an infinite graph has a dual graph and we settle this problem completely in the locally finite case. We show by examples that Tutte’s criterion involving non-separating cy- cles has no immediate extension to infinite graphs, but we present some analogues of that criterion for special classes of infinite graphs. -

On the Treewidth of Triangulated 3-Manifolds
On the Treewidth of Triangulated 3-Manifolds Kristóf Huszár Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-5445-5057 Jonathan Spreer1 Institut für Mathematik, Freie Universität Berlin Arnimallee 2, 14195 Berlin, Germany [email protected] https://orcid.org/0000-0001-6865-9483 Uli Wagner Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-1494-0568 Abstract In graph theory, as well as in 3-manifold topology, there exist several width-type parameters to describe how “simple” or “thin” a given graph or 3-manifold is. These parameters, such as pathwidth or treewidth for graphs, or the concept of thin position for 3-manifolds, play an important role when studying algorithmic problems; in particular, there is a variety of problems in computational 3-manifold topology – some of them known to be computationally hard in general – that become solvable in polynomial time as soon as the dual graph of the input triangulation has bounded treewidth. In view of these algorithmic results, it is natural to ask whether every 3-manifold admits a triangulation of bounded treewidth. We show that this is not the case, i.e., that there exists an infinite family of closed 3-manifolds not admitting triangulations of bounded pathwidth or treewidth (the latter implies the former, but we present two separate proofs). We derive these results from work of Agol and of Scharlemann and Thompson, by exhibiting explicit connections between the topology of a 3-manifold M on the one hand and width-type parameters of the dual graphs of triangulations of M on the other hand, answering a question that had been raised repeatedly by researchers in computational 3-manifold topology. -
5 Graph Theory
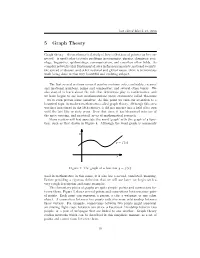
last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples. -

SELF-DUAL GRAPHS 1. Self-Duality of Graphs 1.1. Forms of Self
SELF-DUAL GRAPHS BRIGITTE SERVATIUS AND HERMAN SERVATIUS Abstract. We consider the three forms of self-duality that can be exhibited by a planar graph G, map self-duality, graph self-duality and matroid self- duality. We show how these concepts are related with each other and with the connectivity of G. We use the geometry of self-dual polyhedra together with the structure of the cycle matroid to construct all self-dual graphs. 1. Self-Duality of Graphs 1.1. Forms of Self-duality. Given a planar graph G = (V, E), any regular em- bedding of the topological realization of G into the sphere partitions the sphere into regions called the faces of the embedding, and we write the embedded graph, called a map, as M = (V, E, F ). G may have loops and parallel edges. Given a map M, we form the dual map, M ∗ by placing a vertex f ∗ in the center of each face f, and for ∗ each edge e of M bounding two faces f1 and f2, we draw a dual edge e connecting ∗ ∗ the vertices f1 and f2 and crossing e once transversely. Each vertex v of M will then correspond to a face v∗ of M ∗ and we write M ∗ = (F ∗,E∗,V ∗). If the graph G has distinguishable embeddings, then G may have more than one dual graph, see Figure 1. In this example a portion of the map (V, E, F ) is flipped over on a Q ¡@A@ ¡BB Q ¡ sA @ ¡ sB QQ ¨¨ HH H ¨¨PP ¨¨ ¨ H H ¨ H@ HH¨ @ PP ¨ B¨¨ HH HH HH ¨¨ ¨¨ H HH H ¨¨PP ¨ @ Hs ¨s @¨c H c @ Hs ¢¢ HHs @¨c P@Pc¨¨ s s c c c c s s c c c c @ A ¡ @ A ¢ @s@A ¡ s c c @s@A¢ s c c ∗ ∗ ∗ ∗ 0 ∗ 0∗ ∗ ∗ (V, E,s F ) −→ (F ,E ,V ) (V, E,s F ) −→ (F ,E ,V ) Figure 1. -

Master's Thesis
Master's thesis BWO: Wiskunde∗ A search for the regular tessellations of closed hyperbolic surfaces Student: Benny John Aalders 1st supervisor: Prof. dr. Gert Vegter 2nd supervisor: Dr. Alef Sterk 31st August 2017 ∗Part of the master track: Educatie en Communicatie in de Wiskunde en Natuur- wetenschappen Abstract In this thesis we study regular tessellations of closed orientable surfaces of genus 2 and higher. We differentiate between a purely topological setting and a metric setting. In the topological setting we will describe an algorithm that finds all possible regular tessellations. We also provide the output of this algorithm for genera 2 up to and including 10. In the metric setting we will prove that all topological regular tessellations can be realized metrically. Our method provides an alternative to that of Edmonds, Ewing and Kulkarni. Contents 1 Introduction 1 2 Preliminaries 2 2.1 Hyperbolic geometry . .2 2.2 Fundamental domains . .3 2.3 Side pairings . .4 2.4 A brief discussion on Poincar´e'sTheorem . .5 2.5 Riemann Surfaces . .6 2.6 Tessellations . .9 3 Tessellations of a closed orientable genus-2+ surface 14 3.1 Tessellations of a closed orientable genus-2+ surface consisting of one tile . 14 3.2 How to represent a closed orientable genus-2+ surface as a poly- gon. 16 3.3 Find all regular tessellations of a closed orientable genus-2+ surface 17 4 Making metric regular tessellations out of topological regular tessellations 19 4.1 Exploring the possibilities . 19 4.2 Going from topologically regular to metrically regular . 21 Appendices A An Octave script that prints what all possible fp; qg tessellations for some closed orientable genus-g surface are into a file 28 B All regular tessellations of closed orientable surfaces of genus 2 to 10 33 References 52 1 Introduction In this thesis we will show how to find all possible regular tessellations of a genus-g surface, where g ≥ 2 (genus-2+ surfaces for short). -

Matroid Duality from Topological Duality in Surfaces of Nonnegative Euler Characteristic
Wright State University CORE Scholar Mathematics and Statistics Faculty Publications Mathematics and Statistics 9-2002 Matroid Duality from Topological Duality in Surfaces of Nonnegative Euler Characteristic Dan Slilaty Wright State University - Main Campus, [email protected] Follow this and additional works at: https://corescholar.libraries.wright.edu/math Part of the Applied Mathematics Commons, Applied Statistics Commons, and the Mathematics Commons Repository Citation Slilaty, D. (2002). Matroid Duality from Topological Duality in Surfaces of Nonnegative Euler Characteristic. Combinatorics Probability & Computing, 11 (5), 515-528. https://corescholar.libraries.wright.edu/math/23 This Article is brought to you for free and open access by the Mathematics and Statistics department at CORE Scholar. It has been accepted for inclusion in Mathematics and Statistics Faculty Publications by an authorized administrator of CORE Scholar. For more information, please contact [email protected]. Combinatorics, Probability and Computing (2002) 11, 515–528. c 2002 Cambridge University Press DOI: 10.1017/S0963548302005278 Printed in the United Kingdom Matroid Duality from Topological Duality in Surfaces of Nonnegative Euler Characteristic DANIEL C. SLILATY Department of Mathematics and Statistics, Wright State University, Dayton, OH 45435, USA (e-mail: [email protected]) Received 13 June 2001; revised 11 February 2002 Let G be a connected graph that is 2-cell embedded in a surface S, and let G∗ be its topological dual graph. We will define and discuss several matroids whose element set is E(G), for S homeomorphic to the plane, projective plane, or torus. We will also state and prove old and new results of the type that the dual matroid of G is the matroid of the topological dual G∗. -

Regular Edge Labelings and Drawings of Planar Graphs
Regular Edge Labelings and Drawings of Planar Graphs Xin He 1 and Ming-Yang Kao 2 1 Department of Computer Science, State University of New York at Buffalo, Buffalo, NY 14260. Research supported in part by NSF grant CCR-9205982. 2 Department of Computer Science, Duke University, Durham, NC 27706. Research supported in part by NSF grant CCR-9101385. Abstract. The problems of nicely drawing planar graphs have received increasing attention due to their broad applications [5]. A technique, reg- ular edge labeling, was successfully used in solving several planar graph drawing problems, including visibility representation, straight-line embed- ding, and rectangular dual problems. A regular edge labeling of a plane graph G labels the edges of G so that the edge labels around any vertex show certain regular pattern. The drawing of G is obtained by using the combinatorial structures resulting from the edge labeling. In this paper, we survey these drawing algorithms and discuss some open problems. 1 Visibility Representation Given a planar graph G = (V, E), a visibility representation (VR) of G maps each vertex of G into a horizontal line segment and each edge into a vertical line segment that only touches the two horizontal line segments representing its end vertices. This representation has been used in several applications for representing electrical diagrams and schemes [28]. Linear time algorithms for constructing a VR has been independently discovered by Rosenstiehl and Tarjan [20] and Tamassia and Tollis [29]. Their algorithms are based on: Definition 1: Let G be a connected plane graph and s, t be two vertices on the exterior face of G. -

Graphs in Nature
Graphs in Nature David Eppstein University of California, Irvine Algorithms and Data Structures Symposium (WADS) August 2019 Inspiration: Steinitz's theorem Purely combinatorial characterization of geometric objects: Graphs of convex polyhedra are exactly the 3-vertex-connected planar graphs Image: Kluka [2006] Overview Cracked surfaces, bubble foams, and crumpled paper also form natural graph-like structures What properties do these graphs have? How can we recognize and synthesize them? I. Cracks and Needles Motorcycle graphs: Canonical quad mesh partitioning Problem: partition irregular quad-mesh into regular submeshes [Eppstein et al. 2008] Inspiration: Light cycle game from TRON movies Mesh partitioning method Grow cut paths outwards from each irregular (non-degree-4) vertex Cut paths continue straight across regular (degree-4) vertices They stop when they run into another path Result: approximation to optimal partition (exact optimum is NP-complete) Mesh-free motorcycle graphs Earlier... Motorcycles move from initial points with given velocities When they hit trails of other motorcycles, they crash [Eppstein and Erickson 1999] Application of mesh-free motorcycle graphs Initially: A simplified model of the inward movement of reflex vertices in straight skeletons, a rectilinear variant of medial axes with applications including building roof construction, folding and cutting problems, surface interpolation, geographic analysis, and mesh construction Later: Subroutine for constructing straight skeletons of simple polygons [Cheng and Vigneron 2007; Huber and Held 2012] Image: Huber [2012] Construction of mesh-free motorcycle graphs Main ideas: Define asymmetric distance: Time when one motorcycle would crash into another's trail Repeatedly find closest pair and eliminate crashed motorcycle Image: Dancede [2011] O(n17=11+) [Eppstein and Erickson 1999] Improved to O(n4=3+) [Vigneron and Yan 2014] Additional log speedup using mutual nearest neighbors instead of closest pairs [Mamano et al. -

On the Dual Graph of Cohen-Macaulay Algebras
On the dual graphs of Cohen–Macaulay algebras Bruno Benedetti ∗ Matteo Varbaro ∗∗ Dept. Mathematik u. Informatik, FU Berlin Dip. Matematica, U. Genova [email protected] [email protected] September 25, 2018 Abstract Given an equidimensional algebraic set X Pn, its dual graph G(X) is the ⊂ graph whose vertices are the irreducible components of X and whose edges connect components that intersect in codimension one. Hartshorne’s connectedness theorem says that if (the coordinate ring of) X is Cohen-Macaulay, then G(X) is connected. We present two quantitative variants of Hartshorne’s result: (1) If X is a Gorenstein subspace arrangement, then G(X) is r-connected, where r is the Castelnuovo–Mumford regularity of X. (The bound is best possible. For coordinate arrangements, it yields an algebraic extension of Balinski’s theorem for simplicial polytopes.) (2) If X is an arrangement of lines no three of which meet in the same point, and X is canonically embedded in Pn, then the diameter of the graph G(X) is less than or equal to codimPn X. (The bound is sharp; for coordinate arrangements, it yields an algebraic expan- sion on the recent combinatorial result that the Hirsch conjecture holds for flag normal simplicial complexes.) On the way to these results, we show that there exists a graph which is not the dual graph of any simplicial complex (no matter the dimension). 1 Introduction arXiv:1403.3241v3 [math.AC] 17 Oct 2014 Let I be an ideal in the polynomial ring S = K[x1,...,xn], where K is some field. -

Elementary Graph Theory
Elementary Graph Theory Robin Truax March 2020 Contents 1 Basic Definitions 2 1.1 Specific Types of Graphs . .2 1.2 Paths and Cycles . .3 1.3 Trees and Forests . .3 1.4 Directed Graphs and Route Planning . .4 2 Finding Cycles and Trails 5 2.1 Eulerian Circuits and Eulerian Trails . .5 2.2 Hamiltonian Cycles . .6 3 Planar Graphs 6 3.1 Polyhedra and Projections . .7 3.2 Platonic Solids . .8 4 Ramsey Theory 9 4.1 Ramsey's Theorem . .9 4.2 An Application of Ramsey's Theorem . 10 4.3 Schur's Theorem and a Corollary . 10 5 The Lindstr¨om-Gessel-ViennotLemma 11 5.1 Proving the Lindstr¨om-Gessel-ViennotLemma . 11 5.2 An Application in Linear Algebra . 12 5.3 An Application in Tiling . 13 6 Coloring Graphs 13 6.1 The Five-Color Theorem . 14 7 Extra Topics 15 7.1 Matchings . 15 1 1 Basic Definitions Definition 1 (Graphs). A graph G is a pair (V; E) where V is the set of vertices and E is a list of \edges" (undirected line segments) between pairs of (not necessarily distinct) vertices. Definition 2 (Simple Graphs). A graph G is called a simple graph if there is at most one edge between any two vertices and if no edge starts and ends at the same vertex. Below is an example of a very famous graph, called the Petersen graph, which happens to be simple: Right now, our definitions have a key flaw: two graphs that have exactly the same setup, except one vertex is a quarter-inch to the left, are considered completely different. -

The Point-Set Embeddability Problem for Plane Graphs∗
The Point-set embeddability Problem for Plane Graphs∗ Therese Biedl† Martin Vatshelle‡ Technical Report CS-2011-27 Abstract In this paper, we study the Point-set embeddability-problem, i.e., given a planar graph and a set of points, is there a mapping of the vertices to the points such that the resulting straight-line drawing is planar? This problem is NP-hard if the embedding can be chosen, but becomes polynomial for triangulated graphs of treewidth 3. We show here that in fact it can be answered for all planar graphs with a fixed embedding that have constant treewidth and constant face-degree. We also prove that as soon as one of the conditions is dropped (i.e., either the treewidth is unbounded or some faces have large degrees), Point-set embeddability with a fixed em- bedding becomes NP-hard. The NP-hardness holds even for a 3-connected planar graph with constant treewidth, triangulated planar graphs, or 2-connected outer-planar graphs. ∗The authors would like Dimitrios Thilikos for helpful input. †David R. Cheriton School of Computer Science, University of Waterloo, Waterloo, ON N2L 1A2, Canada. [email protected]. Research supported by NSERC and by the Ross and Muriel Cheriton fellowship. ‡Institute for Informatik, University of Bergen, Norway. [email protected]. Research done while visiting the University of Waterloo. 1 1 Introduction Planar graph drawing is the art of drawing a graph in the two-dimensional plane such that no two edges cross. It has been known for many decades that any planar graph can be drawn with straight lines without crossing [25, 9, 22].