DOCSLIB.ORG

Three Colors Suffice: Conflict-Free Coloring of Planar Graphs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Three Colors Suffice: Conflict-Free Coloring of Planar Graphs Three Colors Suffice: Conflict-Free Coloring of Planar Graphs The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Abel, Zachary, et al. "Three Colors Suffice: Conflict-Free Coloring of Planar Graphs." Proceedings of the Twenty-Eighth Annual ACM- SIAM Symposium on Discrete Algorithms, 16-19 January, 2017, Barcelona, Spain, Society for Industrial and Applied Mathematics, 2017, pp. 1951–63. As Published http://dx.doi.org/10.1137/1.9781611974782.127 Version Author's final manuscript Citable link http://hdl.handle.net/1721.1/114769 Terms of Use Creative Commons Attribution-Noncommercial-Share Alike Detailed Terms http://creativecommons.org/licenses/by-nc-sa/4.0/ Three Colors Suffice: Conflict-Free Coloring of Planar Graphs Zachary Abel∗ Victor Alvarezy Erik D. Demainez Sándor P. Feketey Aman Gourx Adam Hesterberg∗ Phillip Keldenichy Christian Scheffery Abstract a planar graph [5, 6, 26] was a tantalizing open problem A conflict-free k-coloring of a graph assigns one of k for more than 100 years; the quest for solving this chal- different colors to some of the vertices such that, for lenge contributed to the development of graph theory, every vertex v, there is a color that is assigned to exactly but also to computers in theorem proving [29]. A gener- one vertex among v and v’s neighbors. Such colorings alization that is still unsolved is the Hadwiger Conjec- have applications in wireless networking, robotics, and ture [18]: A graph is k-colorable if it has no Kk+1 minor. geometry, and are well-studied in graph theory. Here we Over the years, there have been many variations study the natural problem of the conflict-free chromatic on coloring, often motivated by particular applications. One such context is wireless communication, where number χCF (G) (the smallest k for which conflict-free k-colorings exist), with a focus on planar graphs. “colors” correspond to different frequencies. This also For general graphs, we prove the conflict-free vari- plays a role in robot navigation, where different beacons ant of the famous Hadwiger Conjecture: If G does not are used for providing direction. To this end, it is vital that in any given location, a robot is adjacent to a contain Kk+1 as a minor, then χCF (G) k. For planar graphs, we obtain a tight worst-case bound:≤ three colors beacon with a frequency that is unique among the ones are sometimes necessary and always sufficient. In addi- that can be received. This notion has been introduced tion, we give a complete characterization of the algorith- as conflict-free coloring, formalized as follows. For any vertex v V of a simple graph G = (V; E), the closed mic/computational complexity of conflict-free coloring. 2 It is NP-complete to decide whether a planar graph has neighborhood N[v] consists of all vertices adjacent to v a conflict-free coloring with one color, while for outer- and v itself. A conflict-free k-coloring of G assigns one of k different colors to a (possibly proper) subset S V planar graphs, this can be decided in polynomial time. ⊆ Furthermore, it is NP-complete to decide whether a pla- of vertices, such that for every vertex v V , there is a vertex y N[v], called the conflict-free2 neighbor nar graph has a conflict-free coloring with two colors, 2 while for outerplanar graphs, two colors always suffice. of v, such that the color of y is unique in the closed For the bicriteria problem of minimizing the number of neighborhood of v. The conflict-free chromatic number colored vertices subject to a given bound k on the num- χCF (G) of G is the smallest k for which a conflict-free ber of colors, we give a full algorithmic characterization coloring exists. Observe that χCF (G) is bounded from in terms of complexity and approximation for outerpla- above by the proper chromatic number χ(G) because nar and planar graphs. in a proper coloring, every vertex is its own conflict- arXiv:1701.05999v1 [cs.DM] 21 Jan 2017 free neighbor. 1 Introduction Conflict-free coloring has received an increasing amount of attention. Because of the relationship to Coloring the vertices of a graph is one of the fundamen- classic coloring, it is natural to investigate the conflict- tal problems in graph theory, both scientifically and his- free coloring of planar graphs. In addition, previous torically. Proving that four colors always suffice to color work has considered either general graphs and hyper- graphs (e.g., see [25]) or geometric scenarios (e.g., see ∗Mathematics Department, MIT, Cambridge, Mas- [20]); we give a more detailed overview further down. sachusetts, USA This adds to the relevance of conflict-free coloring of yAlgorithms Group, TU Braunschweig, Braun- planar graphs, which constitute the intersection of gen- schweig, Germany eral graphs and geometry. In addition, the subclass of zComputer Science and Artificial Intelligence Laboratory, MIT, Massachusetts, USA outerplanar graphs is of interest, as it corresponds to xComputer Science and Engineering, IIT Bombay, Mum- subdividing simple polygons by chords. bai, India There is a spectrum of different scientific challenges avoid interference, there must be at least one base sta- when studying conflict-free coloring. What are worst- tion in range using a unique frequency for every point case bounds on the necessary number of colors? When in the entire covered area. The task is to assign a fre- is it NP-hard to determine the existence of a conflict- quency to each base station minimizing the number of free k-coloring, when polynomially solvable? What frequencies. On an abstract level, this induces a color- can be said about approximation? Are there sufficient ing problem on a hypergraph where the base stations conditions for more general graphs? And what can be correspond to the vertices and there is an hyperedge said about the bicriteria problem, in which also the between some vertices if the range of the corresponding number of colored vertices is considered? We provide base stations has a non-empty common intersection. extensive answers for all of these aspects, basically If the hypergraph is induced by disks, Even et providing a complete characterization for planar and al. [15] prove that (log n) colors are always sufficient. outerplanar graphs. Alon and SmorodinskyO [4] extend this by showing that each family of disks, where each disk intersects at most 1.1 Our contribution. We present the following k others, can be colored using (log3 k) colors. Further- results. more, for unit disks, Lev-TovO and Peleg [23] present an (1)-approximation algorithm for the number of colors. 1. For general graphs, we provide the conflict-free HorevO et al. [21] extend this by showing that any set of variant of the Hadwiger Conjecture: If G does not n disks can be colored with (k log n) colors, even if O contain Kk+1 as a minor, then χCF (G) k. every point must see k distinct unique colors. Abam et ≤ al. [1] discuss the problem in the context of cellular net- 2. It is NP-complete to decide whether a planar graph works where the network has to be reliable even if some has a conflict-free coloring with one color. For number of base stations fault, giving worst-case bounds outerplanar graphs, this question can be decided for the number of colors required. in polynomial time. For the dual problem of coloring a set of points such that each region from some family of regions con- 3. It is NP-complete to decide whether a planar graph tains at least one uniquely colored point, Har-Peled and has a conflict-free coloring with two colors. For Smorodinsky [19] prove that with respect to every fam- outerplanar graphs, two colors always suffice. ily of pseudo-disks, every set of points can be colored 4. Three colors are sometimes necessary and always using (log n) colors. For rectangle ranges, Elbassioni O sufficient for conflict-free coloring of a planar graph. and Mustafa [14] show that it is possible to add a sub- linear number of points such that a conflict-free color- 3=8 (1+") 5. For the bicriteria problem of minimizing the num- ing with (n · ) colors becomes possible. Ajwani ber of colored vertices subject to a given bound et al. [2]O complement this by showing that coloring a χ (G) k with k 1; 2 , we prove that the set of points with respect to rectangle ranges is always CF ≤ 2 f g problem is NP-hard for planar and polynomially possible using (n0:382) colors. For coloring points on solvable in outerplanar graphs. a line with respectO to intervals, Cheilaris et al. [10] 2 present a 2-approximation algorithm, and a 5 k - 6. For planar graphs and k = 3 colors, minimizing approximation algorithm when every interval must− see the number of colored vertices does not have a k uniquely colored vertices. Hoffman et al. [20] give constant-factor approximation, unless P = NP. tight bounds for the conflict-free chromatic art gallery problem under rectangular visibility in orthogonal poly- 7. For planar graphs and k 4 colors, it is NP- gons: Θ(log log n) are sometimes necessary and always complete to minimize the number≥ of colored ver- sufficient. Chen et al. [13] consider the online version tices. The problem is fixed-parameter tractable of the conflict-free coloring of a set of points on the (FPT) and allows a PTAS. line, where each newly inserted point must be assigned a color upon insertion, and at all times the coloring has 1.2 Related work.
Load more

Recommended publications
  • K-Outerplanar Graphs, Planar Duality, and Low Stretch Spanning Trees
    k-Outerplanar Graphs, Planar Duality, and Low Stretch Spanning Trees Yuval Emek∗ Abstract Low distortion probabilistic embedding of graphs into approximating trees is an extensively studied topic. Of particular interest is the case where the approximating trees are required to be (subgraph) spanning trees of the given graph (or multigraph), in which case, the focus is usually on the equivalent problem of finding a (single) tree with low average stretch. Among the classes of graphs that received special attention in this context are k-outerplanar graphs (for a fixed k): Chekuri, Gupta, Newman, Rabinovich, and Sinclair show that every k-outerplanar graph can be probabilistically embedded into approximating trees with constant distortion regardless of the size of the graph. The approximating trees in the technique of Chekuri et al. are not necessarily spanning trees, though. In this paper it is shown that every k-outerplanar multigraph admits a spanning tree with constant average stretch. This immediately translates to a constant bound on the distortion of probabilistically embedding k-outerplanar graphs into their spanning trees. Moreover, an efficient randomized algorithm is presented for constructing such a low average stretch spanning tree. This algorithm relies on some new insights regarding the connection between low average stretch spanning trees and planar duality. Keywords: planar graphs, outerplanarity, average stretch, planar dual. ∗Microsoft Israel R&D Center, Herzelia, Israel and School of Electrical Engineering, Tel Aviv University, Tel Aviv, Israel. E-mail: [email protected]. Supported in part by the Israel Science Foundation, grants 221/07 and 664/05. 1 Introduction The problem.
    [Show full text]
  • Characterizations of Restricted Pairs of Planar Graphs Allowing Simultaneous Embedding with Fixed Edges
    Characterizations of Restricted Pairs of Planar Graphs Allowing Simultaneous Embedding with Fixed Edges J. Joseph Fowler1, Michael J¨unger2, Stephen Kobourov1, and Michael Schulz2 1 University of Arizona, USA {jfowler,kobourov}@cs.arizona.edu ⋆ 2 University of Cologne, Germany {mjuenger,schulz}@informatik.uni-koeln.de ⋆⋆ Abstract. A set of planar graphs share a simultaneous embedding if they can be drawn on the same vertex set V in the Euclidean plane without crossings between edges of the same graph. Fixed edges are common edges between graphs that share the same simple curve in the simultaneous drawing. Determining in polynomial time which pairs of graphs share a simultaneous embedding with fixed edges (SEFE) has been open. We give a necessary and sufficient condition for when a pair of graphs whose union is homeomorphic to K5 or K3,3 can have an SEFE. This allows us to determine which (outer)planar graphs always an SEFE with any other (outer)planar graphs. In both cases, we provide efficient al- gorithms to compute the simultaneous drawings. Finally, we provide an linear-time decision algorithm for deciding whether a pair of biconnected outerplanar graphs has an SEFE. 1 Introduction In many practical applications including the visualization of large graphs and very-large-scale integration (VLSI) of circuits on the same chip, edge crossings are undesirable. A single vertex set can be used with multiple edge sets that each correspond to different edge colors or circuit layers. While the pairwise union of all edge sets may be nonplanar, a planar drawing of each layer may be possible, as crossings between edges of distinct edge sets are permitted.
    [Show full text]
  • Minor-Closed Graph Classes with Bounded Layered Pathwidth
    Minor-Closed Graph Classes with Bounded Layered Pathwidth Vida Dujmovi´c z David Eppstein y Gwena¨elJoret x Pat Morin ∗ David R. Wood { 19th October 2018; revised 4th June 2020 Abstract We prove that a minor-closed class of graphs has bounded layered pathwidth if and only if some apex-forest is not in the class. This generalises a theorem of Robertson and Seymour, which says that a minor-closed class of graphs has bounded pathwidth if and only if some forest is not in the class. 1 Introduction Pathwidth and treewidth are graph parameters that respectively measure how similar a given graph is to a path or a tree. These parameters are of fundamental importance in structural graph theory, especially in Roberston and Seymour's graph minors series. They also have numerous applications in algorithmic graph theory. Indeed, many NP-complete problems are solvable in polynomial time on graphs of bounded treewidth [23]. Recently, Dujmovi´c,Morin, and Wood [19] introduced the notion of layered treewidth. Loosely speaking, a graph has bounded layered treewidth if it has a tree decomposition and a layering such that each bag of the tree decomposition contains a bounded number of vertices in each layer (defined formally below). This definition is interesting since several natural graph classes, such as planar graphs, that have unbounded treewidth have bounded layered treewidth. Bannister, Devanny, Dujmovi´c,Eppstein, and Wood [1] introduced layered pathwidth, which is analogous to layered treewidth where the tree decomposition is arXiv:1810.08314v2 [math.CO] 4 Jun 2020 required to be a path decomposition.
    [Show full text]
  • NP-Completeness of List Coloring and Precoloring Extension on the Edges of Planar Graphs
    NP-completeness of list coloring and precoloring extension on the edges of planar graphs D´aniel Marx∗ 17th October 2004 Abstract In the edge precoloring extension problem we are given a graph with some of the edges having a preassigned color and it has to be decided whether this coloring can be extended to a proper k-edge-coloring of the graph. In list edge coloring every edge has a list of admissible colors, and the question is whether there is a proper edge coloring where every edge receives a color from its list. We show that both problems are NP-complete on (a) planar 3-regular bipartite graphs, (b) bipartite outerplanar graphs, and (c) bipartite series-parallel graphs. This improves previous results of Easton and Parker [6], and Fiala [8]. 1 Introduction In graph vertex coloring we have to assign colors to the vertices such that neighboring vertices receive different colors. Starting with [7] and [28], a gener- alization of coloring was investigated: in the list coloring problem each vertex can receive a color only from its prescribed list of admissible colors. In the pre- coloring extension problem a subset W of the vertices have preassigned colors and we have to extend this precoloring to a proper coloring of the whole graph, using only colors from a given color set C. It can be viewed as a special case of list coloring: the list of a precolored vertex consists of a single color, while the list of every other vertex is C. A thorough survey on list coloring, precoloring extension, and list chromatic number can be found in [26, 1, 12, 13].
    [Show full text]
  • Ma/CS 6B Class 8: Planar and Plane Graphs
    1/26/2017 Ma/CS 6b Class 8: Planar and Plane Graphs By Adam Sheffer The Utilities Problem Problem. There are three houses on a plane. Each needs to be connected to the gas, water, and electricity companies. ◦ Is there a way to make all nine connections without any of the lines crossing each other? ◦ Using a third dimension or sending connections through a company or house is not allowed. 1 1/26/2017 Rephrasing as a Graph How can we rephrase the utilities problem as a graph problem? ◦ Can we draw 퐾3,3 without intersecting edges. Closed Curves A simple closed curve (or a Jordan curve) is a curve that does not cross itself and separates the plane into two regions: the “inside” and the “outside”. 2 1/26/2017 Drawing 퐾3,3 with no Crossings We try to draw 퐾3,3 with no crossings ◦ 퐾3,3 contains a cycle of length six, and it must be drawn as a simple closed curve 퐶. ◦ Each of the remaining three edges is either fully on the inside or fully on the outside of 퐶. 퐾3,3 퐶 No 퐾3,3 Drawing Exists We can only add one red-blue edge inside of 퐶 without crossings. Similarly, we can only add one red-blue edge outside of 퐶 without crossings. Since we need to add three edges, it is impossible to draw 퐾3,3 with no crossings. 퐶 3 1/26/2017 Drawing 퐾4 with no Crossings Can we draw 퐾4 with no crossings? ◦ Yes! Drawing 퐾5 with no Crossings Can we draw 퐾5 with no crossings? ◦ 퐾5 contains a cycle of length five, and it must be drawn as a simple closed curve 퐶.
    [Show full text]
  • Star Coloring Outerplanar Bipartite Graphs
    Discussiones Mathematicae Graph Theory 39 (2019) 899–908 doi:10.7151/dmgt.2109 STAR COLORING OUTERPLANAR BIPARTITE GRAPHS Radhika Ramamurthi and Gina Sanders Department of Mathematics California State University San Marcos San Marcos, CA 92096-0001 USA e-mail: [email protected] Abstract A proper coloring of the vertices of a graph is called a star coloring if at least three colors are used on every 4-vertex path. We show that all outerplanar bipartite graphs can be star colored using only five colors and construct the smallest known example that requires five colors. Keywords: chromatic number, star coloring, outerplanar bipartite graph. 2010 Mathematics Subject Classification: 05C15. 1. Introduction A proper r-coloring of a graph G is an assignment of labels from {1, 2,...,r} to the vertices of G so that adjacent vertices receive distinct colors. The minimum r so that G has a proper r-coloring is called the chromatic number of G, denoted by χ(G). The chromatic number is one of the most studied parameters in graph theory, and by convention, the term coloring of a graph is usually used instead of proper coloring. In 1973, Gr¨unbaum [5] considered proper colorings with the additional constraint that the subgraph induced by every pair of color classes is acyclic, i.e., contains no cycles. He called such colorings acyclic colorings, and the minimum r such that G has an acyclic r-coloring is called the acyclic chromatic number of G, denoted by a(G). In introducing the notion of an acyclic coloring, Gr¨unbaum noted that the condition that the union of any two color classes induces a forest can be generalized to other bipartite graphs.
    [Show full text]
  • Planarity and Duality of Finite and Infinite Graphs
    JOURNAL OF COMBINATORIAL THEORY, Series B 29, 244-271 (1980) Planarity and Duality of Finite and Infinite Graphs CARSTEN THOMASSEN Matematisk Institut, Universitets Parken, 8000 Aarhus C, Denmark Communicated by the Editors Received September 17, 1979 We present a short proof of the following theorems simultaneously: Kuratowski’s theorem, Fary’s theorem, and the theorem of Tutte that every 3-connected planar graph has a convex representation. We stress the importance of Kuratowski’s theorem by showing how it implies a result of Tutte on planar representations with prescribed vertices on the same facial cycle as well as the planarity criteria of Whit- ney, MacLane, Tutte, and Fournier (in the case of Whitney’s theorem and MacLane’s theorem this has already been done by Tutte). In connection with Tutte’s planarity criterion in terms of non-separating cycles we give a short proof of the result of Tutte that the induced non-separating cycles in a 3-connected graph generate the cycle space. We consider each of the above-mentioned planarity criteria for infinite graphs. Specifically, we prove that Tutte’s condition in terms of overlap graphs is equivalent to Kuratowski’s condition, we characterize completely the infinite graphs satisfying MacLane’s condition and we prove that the 3- connected locally finite ones have convex representations. We investigate when an infinite graph has a dual graph and we settle this problem completely in the locally finite case. We show by examples that Tutte’s criterion involving non-separating cy- cles has no immediate extension to infinite graphs, but we present some analogues of that criterion for special classes of infinite graphs.
    [Show full text]
  • Surviving Rates of Trees and Outerplanar Graphs for the Firefighter Problem
    Surviving rates of trees and outerplanar graphs for the ¯re¯ghter problem Leizhen Cai¤ Yongxi Chengy Elad Verbinz Yuan Zhouz Abstract The ¯re¯ghter problem is a discrete-time game on graphs introduced by Hartnell in an attempt to model the spread of ¯re, diseases, computer viruses and suchlike in a macro-control level. To measure the defence ability of a graph as a whole, Cai and Wang de¯ned the surviving rate of a graph G for the ¯re¯ghter problem to be the average percentage of vertices that can be saved when a ¯re starts randomly at one vertex of G. In this paper, we prove that the surviving rate of every n-vertex outerplanar graph log n is at least 1 ¡ £( n ), which is asymptotically tight. We also show that the greedy log n strategy of Hartnell and Li for trees saves at least 1 ¡ £( n ) percentage of vertices on average for an n-vertex tree. Key words: ¯re¯ghter problem, surviving rate, tree, outerplanar graph 1 Introduction The study of a discrete-time game, the ¯re¯ghter problem, was initiated by Hartnell [7] in 1995 in an attempt to model the spread of ¯re, diseases, computer viruses and suchlike in a macro-control level. At time 0, a ¯re breaks out at a vertex v of a graph G = (V; E). At each subsequent time, a ¯re¯ghter protects one vertex not yet on ¯re, and the ¯re then spreads from all burning vertices to all their unprotected neighbors. The process ends when the ¯re can no longer spread.
    [Show full text]
  • Fractional and Circular Separation Dimension of Graphs
    Fractional and Circular Separation Dimension of Graphs Sarah J. Loeb∗and Douglas B. West† Revised June 2017 Abstract The separation dimension of a graph G, written π(G), is the minimum number of linear orderings of V (G) such that every two nonincident edges are “separated” in some ordering, meaning that both endpoints of one edge appear before both endpoints of the other. We introduce the fractional separation dimension πf (G), which is the minimum of a/b such that some a linear orderings (repetition allowed) separate every two nonincident edges at least b times. In contrast to separation dimension, fractional separation dimension is bounded: always πf (G) 3, with equality if and only if G contains K4. There is no stronger ≤ 3m bound even for bipartite graphs, since πf (Km,m) = πf (Km+1,m) = m+1 . We also compute πf (G) for cycles and some complete tripartite graphs. We show that πf (G) < √2 when G is a tree and present a sequence of trees on which the value tends to 4/3. Finally, we consider analogous problems for circular orderings, where pairs of non- incident edges are separated unless their endpoints alternate. Let π◦(G) be the number of circular orderings needed to separate all pairs and πf◦(G) be the fractional version. Among our results: (1) π◦(G) = 1 if and only G is outerplanar. (2) π◦(G) 2 when 3 ≤ G is bipartite. (3) π◦(Kn) log2 log3(n 1). (4) πf◦(G) 2 for every graph G, with ≥ − 3m 3 ≤ equality if and only if K4 G.
    [Show full text]
  • On the Treewidth of Triangulated 3-Manifolds
    On the Treewidth of Triangulated 3-Manifolds Kristóf Huszár Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-5445-5057 Jonathan Spreer1 Institut für Mathematik, Freie Universität Berlin Arnimallee 2, 14195 Berlin, Germany [email protected] https://orcid.org/0000-0001-6865-9483 Uli Wagner Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-1494-0568 Abstract In graph theory, as well as in 3-manifold topology, there exist several width-type parameters to describe how “simple” or “thin” a given graph or 3-manifold is. These parameters, such as pathwidth or treewidth for graphs, or the concept of thin position for 3-manifolds, play an important role when studying algorithmic problems; in particular, there is a variety of problems in computational 3-manifold topology – some of them known to be computationally hard in general – that become solvable in polynomial time as soon as the dual graph of the input triangulation has bounded treewidth. In view of these algorithmic results, it is natural to ask whether every 3-manifold admits a triangulation of bounded treewidth. We show that this is not the case, i.e., that there exists an infinite family of closed 3-manifolds not admitting triangulations of bounded pathwidth or treewidth (the latter implies the former, but we present two separate proofs). We derive these results from work of Agol and of Scharlemann and Thompson, by exhibiting explicit connections between the topology of a 3-manifold M on the one hand and width-type parameters of the dual graphs of triangulations of M on the other hand, answering a question that had been raised repeatedly by researchers in computational 3-manifold topology.
    [Show full text]
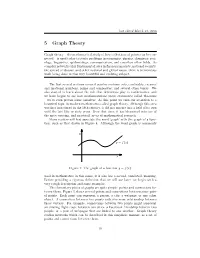
  • 5 Graph Theory
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • Exploring the Earth-Moon Problem for Doubly Outerplanar Graphs
    Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs Maia Wichman Grand Valley State University Partner: Hannah Critchfield, James Madison University Critchfield, Wichman Grand Valley State University REU Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs Overview 1 Background 2 Earth-Moon Problem 3 Specific Cases of Earth-Moon Graphs Critchfield, Wichman Grand Valley State University REU Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs A graph is planar if it can be drawn on the plane without edges crossing. Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs A graph G is a set of vertices V together with a set of edges E which are pairs of vertices. Critchfield, Wichman Grand Valley State University REU Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs A graph is planar if it can be drawn on the plane without edges crossing. Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs A graph G is a set of vertices V together with a set of edges E which are pairs of vertices. Critchfield, Wichman Grand Valley State University REU Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs A graph G is a set of vertices V together with a set of edges E which are pairs of vertices. A graph is planar if it can be drawn on the plane without edges crossing. Critchfield, Wichman Grand Valley State University REU Exploring The Earth-Moon Problem for Doubly Outerplanar Graphs Background Earth-Moon Problem Specific Cases of Earth-Moon Graphs A graph G is a set of vertices V together with a set of edges E which are pairs of vertices.
    [Show full text]