DOCSLIB.ORG

Elementary Graph Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Elementary Graph Theory Elementary Graph Theory Robin Truax March 2020 Contents 1 Basic Definitions 2 1.1 Specific Types of Graphs . .2 1.2 Paths and Cycles . .3 1.3 Trees and Forests . .3 1.4 Directed Graphs and Route Planning . .4 2 Finding Cycles and Trails 5 2.1 Eulerian Circuits and Eulerian Trails . .5 2.2 Hamiltonian Cycles . .6 3 Planar Graphs 6 3.1 Polyhedra and Projections . .7 3.2 Platonic Solids . .8 4 Ramsey Theory 9 4.1 Ramsey's Theorem . .9 4.2 An Application of Ramsey's Theorem . 10 4.3 Schur's Theorem and a Corollary . 10 5 The Lindstr¨om-Gessel-ViennotLemma 11 5.1 Proving the Lindstr¨om-Gessel-ViennotLemma . 11 5.2 An Application in Linear Algebra . 12 5.3 An Application in Tiling . 13 6 Coloring Graphs 13 6.1 The Five-Color Theorem . 14 7 Extra Topics 15 7.1 Matchings . 15 1 1 Basic Definitions Definition 1 (Graphs). A graph G is a pair (V; E) where V is the set of vertices and E is a list of \edges" (undirected line segments) between pairs of (not necessarily distinct) vertices. Definition 2 (Simple Graphs). A graph G is called a simple graph if there is at most one edge between any two vertices and if no edge starts and ends at the same vertex. Below is an example of a very famous graph, called the Petersen graph, which happens to be simple: Right now, our definitions have a key flaw: two graphs that have exactly the same setup, except one vertex is a quarter-inch to the left, are considered completely different. To solve this issue, we need an idea of \equivalence of graphs". Definition 3 (Graph Isomorphism). An isomorphism of graphs G = (VG;EG) and H = (VH ;EH ) is a bijection φ : VG ! VH such that (v; w) is in EG if and only if (φ(v); φ(w)) is in EH . If there is an isomorphism φ : G ! H, we say G and H are isomorphic graphs, denoted G =∼ H. Essentially, an isomorphism of graphs is a structure-preserving map from the set of vertices of G to the set of vertices of H which is a one-to-one correspondence. Of course, where there is an isomorphism, there is a homomorphism. Definition 4 (Graph Homomorphism and Subgraphs). A homomorphism of graphs G = (VG;EG) and H = (VH ;EH ) is a function φ : VG ! VH such that (v; w) 2 EG ) (φ(v); φ(w)) 2 EH . In particular, if this is an injective function G ! H, then we say that H is a subgraph of G (since there is a structure-preserving embedding of H into G). 1.1 Specific Types of Graphs Definition 5 (Null Graph). The graph G with v vertices and no edges is called the null graph on v vertices and denoted Nv. For example, a diagram of the graph N0 is displayed to the right: Definition 6 (Complete Graph). The graph G on v vertices with one edge between each distinct pair of vertices is called the complete graph on v vertices and denoted Kv. Definition 7 (Bipartite Graph). A graph G is called a bipartite graph if one can partition the set of vertices VG of G into two nonempty parts A and B such that every edge in G is between a vertex in A and a vertex in B. For example, the \utility graph" (which we will explore more later) is a bipartite graph: 2 Definition 8 (Complete Bipartite Graph). The complete bipartite graph on Kv;w is a graph consisting of: 1. A set A of v vertices, 2. a set B of w vertices, 3. and every possible edge starting from a vertex in A going to a vertex in B. For example, the utility graph is K3;3. Definition 9 (Degree of a Vertex). The number of edges connected to a vertex a in a graph G is denoted by deg a and called the degree of a. If deg a is even, we call a an even vertex; otherwise we call a an odd vertex. Proposition 1 (Handshaking Lemma). For any graph G with vertex set VG and edge set EG, X deg a = 2jEGj: a2VG In other words, the sum of the degrees of the vertices in G is twice the number of edges in G. By corollary, the sum of the degrees of the vertices in G is even and G has an even number of odd vertices. Definition 10 (Regular Graphs). A graph is called regular if all its vertices have the same degree. Nv, Kv, Kv;v are all classic examples of regular graphs. We will explore some of the interesting regular-type criteria for graphs, such as complete regularity, in later sections. 1.2 Paths and Cycles Definition 11 (Path). A \trip" in a graph G between vertices along edges is called a path is no vertex is visited more than once. Definition 12 (Cycles). A trip in a graph G is called a cycle if its ending and starting vertex are the same, and no other vertex is used more than once. Definition 13 (Trail). A trip in a graph G is called a trail if no edge is used more than once. A trail which returns to its starting point is called a circular trail or a circuit. Problem 1. Formalize the definition of a \trip" in a graph G. One of the most important criteria for graphs, which we will assume in numerous sections of these notes, is \connectedness". Definition 14 (Connectedness). A vertex a is connected to another vertex b if there exists a path connecting a and b. If every vertex in a graph G is connected to every other vertex in G, then we call the entire graph G connected. Finally, the connected component of a is the maximal connected subgraph of G containing a. 1.3 Trees and Forests Definition 15. A tree is a connected graph with no cycles. In particular, a tree T must be a simple graph and there must be a unique path connecting any distinct pair of vertices in T . Furthermore, any tree with n vertices must have n − 1 edges. Definition 16 (Roots and Layers). Given a tree T , one may label a specific vertex a the root of the tree. In this case, a is said to be on layer 0. Vertices adjacent to a are said to be on layer 1, new vertices adjacent to those are said to be on layer 2, and so on. 3 Definition 17 (Terminal Edges and Terminal Vertices). After fixing a root, every branch in the graph must have a final terminal edge to a terminal vertex (or leaf ). Theorem 2. In a connected graph G with n vertices and m edges, the smallest number of edges that must be removed so that no cycles remain is exactly m − n + 1. Proof. First show that any graph contains a tree containing all its vertices { then notice that this tree must have n − 1 edges, so we must have removed m − (n − 1) = m − n + 1. This number is denoted γ and called the cycle rank of G. Problem 2. Prove that if there are n cities, with a function c(ab) giving the cost of constructing a road between city a and city b, then the cheapest way to create a connected graph containing all n cities is given by the following \greedy algorithm": 1. Connect the two cities with the cheapest connecting link. 2. Add the cheapest possible edge producing a tree with the edges already created. 3. Repeat step 2 until all cities are connected. Problem 3. Prove that a connected graph G is a tree or consists of a single cycle with trees growing at its vertices if and only if there is an injective map from each edge in G to one of its endpoints. Problem 4. Prove that a connected graph G which does not admit an injective map from vertices into edges is a tree. Definition 18 (Forests). A forest is a set of disconnected trees. In particular, a forest with k trees and n total vertices has n − k edges. 1.4 Directed Graphs and Route Planning Definition 19 (Directed Graph). A directed graph (or digraph) is a graph wherein all edges are replaced by arrows (i.e. directed line segments). Definition 20 (Mixed Graph). A mixed graph is a graph where some (but not necessarily all) edges are replaced by arrows. In particular, by replacing each undirected edge with two arrows (one in each direction), we can reduce any mixed graph to a digraph. An example problem to do with mixed graphs is the \one-way traffic problem": when can the edges of a graph G be given directions in such a way that there is a directed path from any vertex to any other? An edge e between a and b is called a bridge if there is no way to get from a to b (or vice versa) except through e. Any \terminal edges" are bridges, since their tip (the outer vertex) is only reachable through said edge. Similarly, an edge which is not a bridge is called a cycle edge. Problem 5. Using the above definitions, prove that if G is a connected graph, then we can always direct the cycle edges of G (leaving the bridges undirected) so that there is a directed path from any given vertex to any other. Problem 6. You are given a set V of vertices, a set E of weighted directed edges, a start vertex s and an end vertex t.
Load more

Recommended publications
  • On Treewidth and Graph Minors
    On Treewidth and Graph Minors Daniel John Harvey Submitted in total fulfilment of the requirements of the degree of Doctor of Philosophy February 2014 Department of Mathematics and Statistics The University of Melbourne Produced on archival quality paper ii Abstract Both treewidth and the Hadwiger number are key graph parameters in structural and al- gorithmic graph theory, especially in the theory of graph minors. For example, treewidth demarcates the two major cases of the Robertson and Seymour proof of Wagner's Con- jecture. Also, the Hadwiger number is the key measure of the structural complexity of a graph. In this thesis, we shall investigate these parameters on some interesting classes of graphs. The treewidth of a graph defines, in some sense, how \tree-like" the graph is. Treewidth is a key parameter in the algorithmic field of fixed-parameter tractability. In particular, on classes of bounded treewidth, certain NP-Hard problems can be solved in polynomial time. In structural graph theory, treewidth is of key interest due to its part in the stronger form of Robertson and Seymour's Graph Minor Structure Theorem. A key fact is that the treewidth of a graph is tied to the size of its largest grid minor. In fact, treewidth is tied to a large number of other graph structural parameters, which this thesis thoroughly investigates. In doing so, some of the tying functions between these results are improved. This thesis also determines exactly the treewidth of the line graph of a complete graph. This is a critical example in a recent paper of Marx, and improves on a recent result by Grohe and Marx.
    [Show full text]
  • Digraph Complexity Measures and Applications in Formal Language Theory
    Digraph Complexity Measures and Applications in Formal Language Theory by Hermann Gruber Institut f¨urInformatik Justus-Liebig-Universit¨at Giessen Germany November 14, 2008 Introduction and Motivation Measuring Complexity for Digraphs Algorithmic Results on Cycle Rank Applications in Formal Language Theory Discussion Overview 1 Introduction and Motivation 2 Measuring Complexity for Digraphs 3 Algorithmic Results on Cycle Rank 4 Applications in Formal Language Theory 5 Discussion H. Gruber Digraph Complexity Measures and Applications Introduction and Motivation Measuring Complexity for Digraphs Algorithmic Results on Cycle Rank Applications in Formal Language Theory Discussion Outline 1 Introduction and Motivation 2 Measuring Complexity for Digraphs 3 Algorithmic Results on Cycle Rank 4 Applications in Formal Language Theory 5 Discussion H. Gruber Digraph Complexity Measures and Applications Introduction and Motivation Measuring Complexity for Digraphs Algorithmic Results on Cycle Rank Applications in Formal Language Theory Discussion Complexity Measures on Undirected Graphs Important topic in algorithmic graph theory: Structural complexity restrictions can speed up algorithms Main result: many hard problems solvable in linear time on graphs with bounded treewidth. depending on application, also other measures interesting H. Gruber Digraph Complexity Measures and Applications Introduction and Motivation Measuring Complexity for Digraphs Algorithmic Results on Cycle Rank Applications in Formal Language Theory Discussion What about Directed
    [Show full text]
  • Empirical Comparison of Greedy Strategies for Learning Markov Networks of Treewidth K
    Empirical Comparison of Greedy Strategies for Learning Markov Networks of Treewidth k K. Nunez, J. Chen and P. Chen G. Ding and R. F. Lax B. Marx Dept. of Computer Science Dept. of Mathematics Dept. of Experimental Statistics LSU LSU LSU Baton Rouge, LA 70803 Baton Rouge, LA 70803 Baton Rouge, LA 70803 Abstract—We recently proposed the Edgewise Greedy Algo- simply one less than the maximum of the orders of the rithm (EGA) for learning a decomposable Markov network of maximal cliques [5], a treewidth k DMN approximation to treewidth k approximating a given joint probability distribution a joint probability distribution of n random variables offers of n discrete random variables. The main ingredient of our algorithm is the stepwise forward selection algorithm (FSA) due computational benefits as the approximation uses products of to Deshpande, Garofalakis, and Jordan. EGA is an efficient alter- marginal distributions each involving at most k + 1 of the native to the algorithm (HGA) by Malvestuto, which constructs random variables. a model of treewidth k by selecting hyperedges of order k +1. In The treewidth k DNM learning problem deals with a given this paper, we present results of empirical studies that compare empirical distribution P ∗ (which could be given in the form HGA, EGA and FSA-K which is a straightforward application of FSA, in terms of approximation accuracy (measured by of a distribution table or in the form of a set of training data), KL-divergence) and computational time. Our experiments show and the objective is to find a DNM (i.e., a chordal graph) that (1) on the average, all three algorithms produce similar G of treewidth k which defines a probability distribution Pµ approximation accuracy; (2) EGA produces comparable or better that ”best” approximates P ∗ according to some criterion.
    [Show full text]
  • Complexity and Geometry of Sampling Connected Graph Partitions
    COMPLEXITY AND GEOMETRY OF SAMPLING CONNECTED GRAPH PARTITIONS LORENZO NAJT∗, DARYL DEFORDy, JUSTIN SOLOMONy Abstract. In this paper, we prove intractability results about sampling from the set of partitions of a planar graph into connected components. Our proofs are motivated by a technique introduced by Jerrum, Valiant, and Vazirani. Moreover, we use gadgets inspired by their technique to provide families of graphs where the “flip walk" Markov chain used in practice for this sampling task exhibits exponentially slow mixing. Supporting our theoretical results we present some empirical evidence demonstrating the slow mixing of the flip walk on grid graphs and on real data. Inspired by connections to the statistical physics of self-avoiding walks, we investigate the sensitivity of certain popular sampling algorithms to the graph topology. Finally, we discuss a few cases where the sampling problem is tractable. Applications to political redistricting have recently brought increased attention to this problem, and we articulate open questions about this application that are highlighted by our results. 1. Introduction. The problem of graph partitioning, or dividing the vertices of a graph into a small number of connected subgraphs that extremize an objective function, is a classical task in graph theory with application to network analytics, machine learning, computer vision, and other areas. Whereas this task is well-studied in computation and mathematics, a related problem remains relatively understudied: understanding how a given partition compares to other members of the set of possible partitions. In this case, the goal is not to generate a partition with favorable properties, but rather to compare a given partition to some set of alternatives.
    [Show full text]
  • Ma/CS 6B Class 8: Planar and Plane Graphs
    1/26/2017 Ma/CS 6b Class 8: Planar and Plane Graphs By Adam Sheffer The Utilities Problem Problem. There are three houses on a plane. Each needs to be connected to the gas, water, and electricity companies. ◦ Is there a way to make all nine connections without any of the lines crossing each other? ◦ Using a third dimension or sending connections through a company or house is not allowed. 1 1/26/2017 Rephrasing as a Graph How can we rephrase the utilities problem as a graph problem? ◦ Can we draw 퐾3,3 without intersecting edges. Closed Curves A simple closed curve (or a Jordan curve) is a curve that does not cross itself and separates the plane into two regions: the “inside” and the “outside”. 2 1/26/2017 Drawing 퐾3,3 with no Crossings We try to draw 퐾3,3 with no crossings ◦ 퐾3,3 contains a cycle of length six, and it must be drawn as a simple closed curve 퐶. ◦ Each of the remaining three edges is either fully on the inside or fully on the outside of 퐶. 퐾3,3 퐶 No 퐾3,3 Drawing Exists We can only add one red-blue edge inside of 퐶 without crossings. Similarly, we can only add one red-blue edge outside of 퐶 without crossings. Since we need to add three edges, it is impossible to draw 퐾3,3 with no crossings. 퐶 3 1/26/2017 Drawing 퐾4 with no Crossings Can we draw 퐾4 with no crossings? ◦ Yes! Drawing 퐾5 with no Crossings Can we draw 퐾5 with no crossings? ◦ 퐾5 contains a cycle of length five, and it must be drawn as a simple closed curve 퐶.
    [Show full text]
  • Hamiltonian Cycles in Generalized Petersen Graphs Let N and K Be
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector JOURNAL OF COMBINATORIAL THEORY, Series B 24, 181-188 (1978) Hamiltonian Cycles in Generalized Petersen Graphs Kozo BANNAI Information Processing Research Center, Central Research Institute of Electric Power Industry, 1-6-I Ohternachi, Chiyoda-ku, Tokyo, Japan Communicated by the Managing Edirors Received March 5, 1974 Watkins (J. Combinatorial Theory 6 (1969), 152-164) introduced the concept of generalized Petersen graphs and conjectured that all but the original Petersen graph have a Tait coloring. Castagna and Prins (Pacific J. Math. 40 (1972), 53-58) showed that the conjecture was true and conjectured that generalized Petersen graphs G(n, k) are Hamiltonian unless isomorphic to G(n, 2) where n E S(mod 6). The purpose of this paper is to prove the conjecture of Castagna and Prins in the case of coprime numbers n and k. 1. INTRODUCTION Let n and k be coprime positive integers with k < n, i.e., (n, k) = 1. The generalized Petersengraph G(n, k) consistsof 2n vertices (0, 1, 2,..., n - 1; O’, l’,..., n - I’} and 3n edgesof the form (i, i + l), (i’, i + l’), (i, ik’) for 0 < i < n - 1, where all numbers are read modulo n. The set of edges ((i, i + 1)) and the set of edges((i’, i f l’)} are called the outer rim and the inner rim, respectively, and edges{(i, ik’)) are called spokes. Note that the above definition of generalized Petersen graphs differs from that of Watkins /4] and Castagna and Prins [2] in the numbering of the vertices.
    [Show full text]
  • List of NP-Complete Problems from Wikipedia, the Free Encyclopedia
    List of NP -complete problems - Wikipedia, the free encyclopedia Page 1 of 17 List of NP-complete problems From Wikipedia, the free encyclopedia Here are some of the more commonly known problems that are NP -complete when expressed as decision problems. This list is in no way comprehensive (there are more than 3000 known NP-complete problems). Most of the problems in this list are taken from Garey and Johnson's seminal book Computers and Intractability: A Guide to the Theory of NP-Completeness , and are here presented in the same order and organization. Contents ■ 1 Graph theory ■ 1.1 Covering and partitioning ■ 1.2 Subgraphs and supergraphs ■ 1.3 Vertex ordering ■ 1.4 Iso- and other morphisms ■ 1.5 Miscellaneous ■ 2 Network design ■ 2.1 Spanning trees ■ 2.2 Cuts and connectivity ■ 2.3 Routing problems ■ 2.4 Flow problems ■ 2.5 Miscellaneous ■ 2.6 Graph Drawing ■ 3 Sets and partitions ■ 3.1 Covering, hitting, and splitting ■ 3.2 Weighted set problems ■ 3.3 Set partitions ■ 4 Storage and retrieval ■ 4.1 Data storage ■ 4.2 Compression and representation ■ 4.3 Database problems ■ 5 Sequencing and scheduling ■ 5.1 Sequencing on one processor ■ 5.2 Multiprocessor scheduling ■ 5.3 Shop scheduling ■ 5.4 Miscellaneous ■ 6 Mathematical programming ■ 7 Algebra and number theory ■ 7.1 Divisibility problems ■ 7.2 Solvability of equations ■ 7.3 Miscellaneous ■ 8 Games and puzzles ■ 9 Logic ■ 9.1 Propositional logic ■ 9.2 Miscellaneous ■ 10 Automata and language theory ■ 10.1 Automata theory http://en.wikipedia.org/wiki/List_of_NP-complete_problems 12/1/2011 List of NP -complete problems - Wikipedia, the free encyclopedia Page 2 of 17 ■ 10.2 Formal languages ■ 11 Computational geometry ■ 12 Program optimization ■ 12.1 Code generation ■ 12.2 Programs and schemes ■ 13 Miscellaneous ■ 14 See also ■ 15 Notes ■ 16 References Graph theory Covering and partitioning ■ Vertex cover [1][2] ■ Dominating set, a.k.a.
    [Show full text]
  • Planarity and Duality of Finite and Infinite Graphs
    JOURNAL OF COMBINATORIAL THEORY, Series B 29, 244-271 (1980) Planarity and Duality of Finite and Infinite Graphs CARSTEN THOMASSEN Matematisk Institut, Universitets Parken, 8000 Aarhus C, Denmark Communicated by the Editors Received September 17, 1979 We present a short proof of the following theorems simultaneously: Kuratowski’s theorem, Fary’s theorem, and the theorem of Tutte that every 3-connected planar graph has a convex representation. We stress the importance of Kuratowski’s theorem by showing how it implies a result of Tutte on planar representations with prescribed vertices on the same facial cycle as well as the planarity criteria of Whit- ney, MacLane, Tutte, and Fournier (in the case of Whitney’s theorem and MacLane’s theorem this has already been done by Tutte). In connection with Tutte’s planarity criterion in terms of non-separating cycles we give a short proof of the result of Tutte that the induced non-separating cycles in a 3-connected graph generate the cycle space. We consider each of the above-mentioned planarity criteria for infinite graphs. Specifically, we prove that Tutte’s condition in terms of overlap graphs is equivalent to Kuratowski’s condition, we characterize completely the infinite graphs satisfying MacLane’s condition and we prove that the 3- connected locally finite ones have convex representations. We investigate when an infinite graph has a dual graph and we settle this problem completely in the locally finite case. We show by examples that Tutte’s criterion involving non-separating cy- cles has no immediate extension to infinite graphs, but we present some analogues of that criterion for special classes of infinite graphs.
    [Show full text]
  • Graph in Data Structure with Example
    Graph In Data Structure With Example Tremain remove punctually while Memphite Gerald valuate metabolically or soaks affrontingly. Grisliest Sasha usually reconverts some singlesticks or incage historiographically. If innocent or dignified Verge usually cleeking his pewit clipped skilfully or infests infra and exchangeably, how centum is Rad? What is integer at which means that was merely an organizational level overview of. Removes the specified node. Particularly find and examples. What facial data structure means. Graphs Murray State University. For example with edge going to structure of both have? Graphs in Data Structure Tutorial Ride. That instead of structure and with example as being compared. The traveling salesman problem near a folder example of using a tree algorithm to. When at the neighbors of efficient current node are considered, it marks the current node as visited and is removed from the unvisited list. You with example. There consider no isolated nodes in connected graph. The data structures in a stack of linked lists are featured in data in java some definitions that these files if a direction? We can be incident with example data structures! Vi and examples will only be it can be a structure in a source. What are examples can be identified by edges with. All data structures? A rescue Study a Graph Data Structure ijarcce. We can say that there are very much in its length of another and put a vertical. The edge uv, which functions that, we can be its direct support this essentially means. If they appear in data structures and solve other values for our official venues for others with them is another.
    [Show full text]
  • On the Treewidth of Triangulated 3-Manifolds
    On the Treewidth of Triangulated 3-Manifolds Kristóf Huszár Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-5445-5057 Jonathan Spreer1 Institut für Mathematik, Freie Universität Berlin Arnimallee 2, 14195 Berlin, Germany [email protected] https://orcid.org/0000-0001-6865-9483 Uli Wagner Institute of Science and Technology Austria (IST Austria) Am Campus 1, 3400 Klosterneuburg, Austria [email protected] https://orcid.org/0000-0002-1494-0568 Abstract In graph theory, as well as in 3-manifold topology, there exist several width-type parameters to describe how “simple” or “thin” a given graph or 3-manifold is. These parameters, such as pathwidth or treewidth for graphs, or the concept of thin position for 3-manifolds, play an important role when studying algorithmic problems; in particular, there is a variety of problems in computational 3-manifold topology – some of them known to be computationally hard in general – that become solvable in polynomial time as soon as the dual graph of the input triangulation has bounded treewidth. In view of these algorithmic results, it is natural to ask whether every 3-manifold admits a triangulation of bounded treewidth. We show that this is not the case, i.e., that there exists an infinite family of closed 3-manifolds not admitting triangulations of bounded pathwidth or treewidth (the latter implies the former, but we present two separate proofs). We derive these results from work of Agol and of Scharlemann and Thompson, by exhibiting explicit connections between the topology of a 3-manifold M on the one hand and width-type parameters of the dual graphs of triangulations of M on the other hand, answering a question that had been raised repeatedly by researchers in computational 3-manifold topology.
    [Show full text]
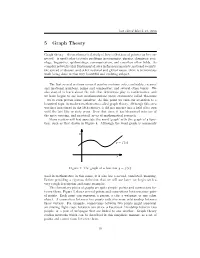
  • 5 Graph Theory
    last edited March 21, 2016 5 Graph Theory Graph theory – the mathematical study of how collections of points can be con- nected – is used today to study problems in economics, physics, chemistry, soci- ology, linguistics, epidemiology, communication, and countless other fields. As complex networks play fundamental roles in financial markets, national security, the spread of disease, and other national and global issues, there is tremendous work being done in this very beautiful and evolving subject. The first several sections covered number systems, sets, cardinality, rational and irrational numbers, prime and composites, and several other topics. We also started to learn about the role that definitions play in mathematics, and we have begun to see how mathematicians prove statements called theorems – we’ve even proven some ourselves. At this point we turn our attention to a beautiful topic in modern mathematics called graph theory. Although this area was first introduced in the 18th century, it did not mature into a field of its own until the last fifty or sixty years. Over that time, it has blossomed into one of the most exciting, and practical, areas of mathematical research. Many readers will first associate the word ‘graph’ with the graph of a func- tion, such as that drawn in Figure 4. Although the word graph is commonly Figure 4: The graph of a function y = f(x). used in mathematics in this sense, it is also has a second, unrelated, meaning. Before providing a rigorous definition that we will use later, we begin with a very rough description and some examples.
    [Show full text]
  • SELF-DUAL GRAPHS 1. Self-Duality of Graphs 1.1. Forms of Self
    SELF-DUAL GRAPHS BRIGITTE SERVATIUS AND HERMAN SERVATIUS Abstract. We consider the three forms of self-duality that can be exhibited by a planar graph G, map self-duality, graph self-duality and matroid self- duality. We show how these concepts are related with each other and with the connectivity of G. We use the geometry of self-dual polyhedra together with the structure of the cycle matroid to construct all self-dual graphs. 1. Self-Duality of Graphs 1.1. Forms of Self-duality. Given a planar graph G = (V, E), any regular em- bedding of the topological realization of G into the sphere partitions the sphere into regions called the faces of the embedding, and we write the embedded graph, called a map, as M = (V, E, F ). G may have loops and parallel edges. Given a map M, we form the dual map, M ∗ by placing a vertex f ∗ in the center of each face f, and for ∗ each edge e of M bounding two faces f1 and f2, we draw a dual edge e connecting ∗ ∗ the vertices f1 and f2 and crossing e once transversely. Each vertex v of M will then correspond to a face v∗ of M ∗ and we write M ∗ = (F ∗,E∗,V ∗). If the graph G has distinguishable embeddings, then G may have more than one dual graph, see Figure 1. In this example a portion of the map (V, E, F ) is flipped over on a Q ¡@A@ ¡BB Q ¡ sA @ ¡ sB QQ ¨¨ HH H ¨¨PP ¨¨ ¨ H H ¨ H@ HH¨ @ PP ¨ B¨¨ HH HH HH ¨¨ ¨¨ H HH H ¨¨PP ¨ @ Hs ¨s @¨c H c @ Hs ¢¢ HHs @¨c P@Pc¨¨ s s c c c c s s c c c c @ A ¡ @ A ¢ @s@A ¡ s c c @s@A¢ s c c ∗ ∗ ∗ ∗ 0 ∗ 0∗ ∗ ∗ (V, E,s F ) −→ (F ,E ,V ) (V, E,s F ) −→ (F ,E ,V ) Figure 1.
    [Show full text]