DOCSLIB.ORG

Electronic Structure of Three Center Two Electron Bonds in Boron

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Electronic Structure of Three Center Two Electron Bonds in Boron ELECTRONIC STRUCTURE OF THREE CENTER TWO ELECTRON BONDS IN BORON RICH MATERIALS: A STUDY OF MOLECULES, CRYSTALS, AND AMORPHOUS SOLIDS USING THE AB INITIO ORTHOGONALIZED LINEAR COMBINATION OF ATOMIC ORBITALS METHOD A THESIS IN Physics Presented to the Faculty of the University of Missouri-Kansas City in partial fulfilment of the requirements for the degree MASTER OF SCIENCE by JOSHUA RAY SEXTON B. S., University of Missouri-Kansas City, 2017 Kansas City, Missouri 2020 © 2020 JOSHUA RAY SEXTON ALL RIGHTS RESERVED ELECTRONIC STRUCTURE OF THREE CENTER TWO ELECTRON BONDS IN BORON RICH MATERIALS: A STUDY OF MOLECULES, CRYSTALS, AND AMORPHOUS SOLIDS USING THE AB INITIO ORTHOGONALIZED LINEAR COMBINATION OF ATOMIC ORBITALS METHOD Joshua Ray Sexton, Candidate for the Master of Science Degree University of Missouri-Kansas City, 2020 ABSTRACT It has been shown that isomers of carborane, α and β rhombohedral boron, α and β tetragonal boron, γ boron, and boron carbide tend to form icosahedral structures. If the icosahedra were formed with pure boron, it has been demonstrated that there is an insufficient number of electrons to populate all the molecular orbitals that would nominally be required for molecular cohesion. To overcome that electron deficiency, the icosahedral boron units tend to form interesting bonding structures with their neighbors in solids, and/or for molecular boron the icosahedra tends to incorporate substitutional carbon atoms. The resultant bonding structures are often of a 3 center 2 electron nature. The visualization of these 3 center 2 electron bonds varies in the literature and this exposes a discontinuity with how multi-center bonds should be perceived. Here, I have attempted to reconcile these delocalized bonds with the common “ball-and-stick” molecular model using an extension to Mulliken Population Analysis within the Orthogonalized Linear Combination of Atomic Orbitals method. iii iv APPROVAL PAGE The Faculty listed below, appointed by the Dean of the College of Arts and Sciences, have examined a thesis titled “Electronic Structure of Three Center Two Electron Bonds in Boron Rich Materials: A Study of Molecules, Crystals, and Amorphous Solids using the ab initio Orthogonalized Linear Combination of Atomic Orbitals Method”, presented by Joshua Ray Sexton, candidate for the Master of Science degree, and certify that in their opinion, it is worthy of acceptance. Supervisory Committee Paul Rulis, Ph.D., Committee Chair Department of Physics and Astronomy Wai-Yim Ching, Ph.D. Department of Physics and Astronomy Michelle Paquette, Ph.D. Department of Physics and Astronomy v Table of Contents ABSTRACT................................................................................................................................................ iii LIST OF TABLES ...................................................................................................................................... x ACKNOWLEDGEMENTS ..................................................................................................................... xi 1. INTRODUCTION .................................................................................................................................. 1 Context ............................................................................................................................ 1 Motivation ....................................................................................................................... 6 Outline ............................................................................................................................. 7 2. METHODS .............................................................................................................................................. 9 The OLCAO Method .................................................................................................... 10 The Visualization ToolKit............................................................................................. 14 Paraview ........................................................................................................................ 16 Program ......................................................................................................................... 17 3. RESULTS AND DISCUSSION ......................................................................................................... 21 Model Systems .............................................................................................................. 21 Carborane C2H10B12 ................................................................................................... 23 α-Rhombohedral Boron ............................................................................................. 24 β-Rhombohedral Boron ............................................................................................. 25 γ-Boron ...................................................................................................................... 27 α-Tetragonal Boron 51 .............................................................................................. 28 β-Tetragonal Boron 190 ............................................................................................ 29 vi Boron Carbide B11C-CBC ......................................................................................... 30 Amorphous Hydrogenated Boron Carbide a-BxC:Hy ................................................ 31 4. CONCLUSIONS AND FUTURE WORK ....................................................................................... 39 Conclusion..................................................................................................................... 39 Future Work .................................................................................................................. 39 APPENDIX ................................................................................................................................................ 41 Created and Altered Scripts and Programs ................................................................... 41 bond3C.F90 ............................................................................................................... 41 insert3cbo .................................................................................................................. 41 makeBOND ............................................................................................................... 42 Custom Paraview Filter ............................................................................................. 43 REFERENCES .......................................................................................................................................... 44 VITA ........................................................................................................................................................... 48 vii LIST OF ILLUSTRATIONS Figure 1 Atomic structure of dodecaborane B12H12 .............................................................4 Figure 2 (A)-(C) Schematic, stereographic, and broad views of α-rhombohedral boron; (D) Bonding charge contours from [6] ........................................................................5 Figure 3 Sample VTK legacy polydata output ..................................................................16 Figure 4 Paraview rendering of Figure 3 ...........................................................................17 Figure 5 Old process of bond visualization .......................................................................19 Figure 5 New process of visualization ...............................................................................20 Figure 6 Traditional visualizations of ortho, para, and meta-carboranes. .........................23 Figure 7 Carboranes new visualization: ortho, para, and meta ..........................................24 Figure 8 Alpha boron traditional visualization ..................................................................24 Figure 9 Alpha boron new visualization ............................................................................25 Figure 10 Beta boron traditional visualization...................................................................25 Figure 11 Beta boron new visualization ............................................................................26 Figure 12 Gamma boron traditional visualization .............................................................27 Figure 13 Gamma boron new visualization .......................................................................27 Figure 14 Alpha tetragonal boron traditional visualization ...............................................28 Figure 15 Alpha tetragonal boron new visualization .........................................................28 Figure 16 Beta tetragonal boron traditional visualization ..................................................29 Figure 17 Beta tetragonal boron new visualization ...........................................................29 Figure 18 Boron Carbide traditional visualization.............................................................30 Figure 19 Boron Carbide new visualization ......................................................................30 viii Figure 20 a-BC:H traditional visualization ........................................................................31 Figure 21 a-BC:H new visualization..................................................................................32
Load more

Recommended publications
  • Topological Analysis of the Metal-Metal Bond: a Tutorial Review Christine Lepetit, Pierre Fau, Katia Fajerwerg, Myrtil L
    Topological analysis of the metal-metal bond: A tutorial review Christine Lepetit, Pierre Fau, Katia Fajerwerg, Myrtil L. Kahn, Bernard Silvi To cite this version: Christine Lepetit, Pierre Fau, Katia Fajerwerg, Myrtil L. Kahn, Bernard Silvi. Topological analysis of the metal-metal bond: A tutorial review. Coordination Chemistry Reviews, Elsevier, 2017, 345, pp.150-181. 10.1016/j.ccr.2017.04.009. hal-01540328 HAL Id: hal-01540328 https://hal.sorbonne-universite.fr/hal-01540328 Submitted on 16 Jun 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Topological analysis of the metal-metal bond: a tutorial review Christine Lepetita,b, Pierre Faua,b, Katia Fajerwerga,b, MyrtilL. Kahn a,b, Bernard Silvic,∗ aCNRS, LCC (Laboratoire de Chimie de Coordination), 205, route de Narbonne, BP 44099, F-31077 Toulouse Cedex 4, France. bUniversité de Toulouse, UPS, INPT, F-31077 Toulouse Cedex 4, i France cSorbonne Universités, UPMC, Univ Paris 06, UMR 7616, Laboratoire de Chimie Théorique, case courrier 137, 4 place Jussieu, F-75005 Paris, France Abstract This contribution explains how the topological methods of analysis of the electron density and related functions such as the electron localization function (ELF) and the electron localizability indicator (ELI-D) enable the theoretical characterization of various metal-metal (M-M) bonds (multiple M-M bonds, dative M-M bonds).
    [Show full text]
  • Effect of High Temperature on Wear Behavior of Stir Cast Aluminium
    Mechanics and Mechanical Engineering Vol. 22, No. 4 (2018) 1031{1046 c Technical University of Lodz https://doi.org/10.2478/mme-2018-0082 Effect of High Temperature on Wear Behavior of Stir Cast Aluminium/Boron Carbide Composites X. Canute and M. C. Majumder Department of Mechanical Engineering, National Institute of Technology, Durgapur, India Received (9 May 2018) Revised (11 December 2018) Accepted (20 December 2018) The need for development of high temperature wear resistant composite materials with superior mechanical properties and tribological properties is increasing significantly. The high temperature wear properties of aluminium boron carbide composites was evaluated in this investigation. The effect of load, sliding velocity, temperature and reinforcement percentage on wear rate was determined by the pin heating method using pin heating arrangement. The size and structure of base alloy particles change considerably with an increase of boron carbide particles. The wettability and interface bonding between the matrix and reinforcement enhanced by the addition of potassium flurotitanate. ANOVA technique was used to study the effect of input parameters on wear rate. The investi- gation reveals that the load had higher significance than sliding velocity, temperature and weight fraction. The pin surface was studied with a high-resolution scanning elec- tron microscope. Regression analysis revealed an extensive association between control parameters and response. The developed composites can be used in the production of automobile parts requiring high wear, frictional and thermal resistance. Keywords: PCM, enhancement melting, eccentric cylinders, fins, LHS. 1. Introduction Metal matrix composites are widely preferred due to yield strength and wear re- sistance for high temperature applications [1].
    [Show full text]
  • Experiments on the Oxidation of Boron Carbide at High Temperatures
    Forschungszentrum Karlsruhe in der Helmholtz-Gemeinschaft Wissenschaftliche Berichte FZKA 6979 Experiments on the Oxidation of Boron Carbide at High Temperatures M. Steinbrück, A. Meier, U. Stegmaier, L. Steinbock Institut für Materialforschung Programm Nukleare Sicherheitsforschung Mai 2004 Forschungszentrum Karlsruhe in der Helmholtz-Gemeinschaft Wissenschaftliche Berichte FZKA 6979 Experiments on the Oxidation of Boron Carbide at High Temperatures M. Steinbrück, A. Meier, U. Stegmaier, L. Steinbock Institut für Materialforschung Programm Nukleare Sicherheitsforschung Forschungszentrum Karlsruhe GmbH, Karlsruhe 2004 Impressum der Print-Ausgabe: Als Manuskript gedruckt Für diesen Bericht behalten wir uns alle Rechte vor Forschungszentrum Karlsruhe GmbH Postfach 3640, 76021 Karlsruhe Mitglied der Hermann von Helmholtz-Gemeinschaft Deutscher Forschungszentren (HGF) ISSN 0947-8620 urn:nbn:de:0005-069792 OXIDATION VON BORKARBID BEI HOHEN TEMPERATUREN ZUSAMMENFASSUNG Borkarbid wird weltweit in verschiedenen Kernreaktoren als Absorbermaterial in Steuer- stäben eingesetzt. Während eines hypothetischen schweren Störfalls führen eutektische Wechselwirkungen zwischen B4C und den umgebenden Hüllrohren aus rostfreiem Stahl schon bei Temperaturen um 1200 °C und somit weit unterhalb der Schmelztemperaturen der einzelnen Komponenten zur Bildung von Schmelzphasen. Das so freigelegte Absorber- material sowie gebildete B4C/Metall-Schmelzen sind dem Dampf im Reaktor ausgesetzt. Die Oxidation von Borkarbid ist stark exotherm und führt zur Bildung von gasförmigen
    [Show full text]
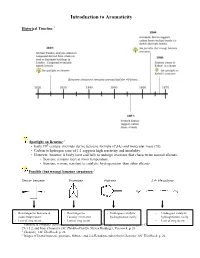
  • Introduction to Aromaticity
    Introduction to Aromaticity Historical Timeline:1 Spotlight on Benzene:2 th • Early 19 century chemists derive benzene formula (C6H6) and molecular mass (78). • Carbon to hydrogen ratio of 1:1 suggests high reactivity and instability. • However, benzene is fairly inert and fails to undergo reactions that characterize normal alkenes. - Benzene remains inert at room temperature. - Benzene is more resistant to catalytic hydrogenation than other alkenes. Possible (but wrong) benzene structures:3 Dewar benzene Prismane Fulvene 2,4- Hexadiyne - Rearranges to benzene at - Rearranges to - Undergoes catalytic - Undergoes catalytic room temperature. Faraday’s benzene. hydrogenation easily. hydrogenation easily - Lots of ring strain. - Lots of ring strain. - Lots of ring strain. 1 Timeline is computer-generated, compiled with information from pg. 594 of Bruice, Organic Chemistry, 4th Edition, Ch. 15.2, and from Chemistry 14C Thinkbook by Dr. Steven Hardinger, Version 4, p. 26 2 Chemistry 14C Thinkbook, p. 26 3 Images of Dewar benzene, prismane, fulvene, and 2,4-Hexadiyne taken from Chemistry 14C Thinkbook, p. 26. Kekulé’s solution: - “snake bites its own tail” (4) Problems with Kekulé’s solution: • If Kekulé’s structure were to have two chloride substituents replacing two hydrogen atoms, there should be a pair of 1,2-dichlorobenzene isomers: one isomer with single bonds separating the Cl atoms, and another with double bonds separating the Cl atoms. • These isomers were never isolated or detected. • Rapid equilibrium proposed, where isomers interconvert so quickly that they cannot be isolated or detected. • Regardless, Kekulé’s structure has C=C’s and normal alkene reactions are still expected. - But the unusual stability of benzene still unexplained.
    [Show full text]
  • Synthesis, Characterization and Energetic Performance
    SYNTHESIS, CHARACTERIZATION AND ENERGETIC PERFORMANCE OF METAL BORIDE COMPOUNDS FOR INSENSITIVE ENERGETIC MATERIALS by Michael L. Whittaker A thesis submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Master of Science Department of Materials Science and Engineering University of Utah May 2012 Copyright © Michael L. Whittaker 2012 All Rights Reserved The University of Utah Graduate School STATEMENT OF THESIS APPROVAL The thesis of Michael L. Whittaker has been approved by the following supervisory committee members: Raymond A. Cutler , Chair 03/09/2012 Date Approved Anil V. Virkar , Member 03/09/2012 Date Approved Gerald B. Stringfellow , Member 03/09/2012 Date Approved and by Feng Liu , Chair of the Department of Materials Science and Engineering and by Charles A. Wight, Dean of The Graduate School. ABSTRACT Six metal boride compounds (AlB2, MgB2, Al0.5Mg0.5B2, AlB12, AlMgB14 and SiB6) with particle sizes between 10-20 m were synthesized for insensitive energetic fuel additives from stoichiometric physical mixtures of elemental powders by high temperature solid state reaction. B4C was also investigated as a lower cost source of boron in AlB2 synthesis and showed promise as a boron substitute. Thermal analysis confirmed that the formation of boride compounds from physical mixtures decreased sensitivity to low temperature oxidation over the aluminum standard. Both Al+2B and AlB2 were much less sensitive to moisture degradation than aluminum in high humidity (10-100% relative humidity) and high temperature (20-80°C) environments. AlB2 was determined to be safe to store for extended periods of time in cool, dry environments.
    [Show full text]
  • Symmetry of Three-Center, Four-Electron Bonds†‡
    Chemical Science EDGE ARTICLE View Article Online View Journal | View Issue Symmetry of three-center, four-electron bonds†‡ b a c Cite this: Chem. Sci., 2020, 11,7979 Ann Christin Reiersølmoen, § Stefano Battaglia, § Sigurd Øien-Ødegaard, Arvind Kumar Gupta, d Anne Fiksdahl,b Roland Lindh a and Mate Erdelyi *a All publication charges for this article ´ ´ ´ have been paid for by the Royal Society of Chemistry Three-center, four-electron bonds provide unusually strong interactions; however, their nature remains ununderstood. Investigations of the strength, symmetry and the covalent versus electrostatic character of three-center hydrogen bonds have vastly contributed to the understanding of chemical bonding, whereas the assessments of the analogous three-center halogen, chalcogen, tetrel and metallic s^-type long bonding are still lagging behind. Herein, we disclose the X-ray crystallographic, NMR spectroscopic and computational investigation of three-center, four-electron [D–X–D]+ bonding for a variety of cations (X+ ¼ H+,Li+,Na+,F+,Cl+,Br+,I+,Ag+ and Au+) using a benchmark bidentate model system. Formation of a three-center bond, [D–X–D]+ is accompanied by an at least 30% shortening of the D–X Received 11th April 2020 bonds. We introduce a numerical index that correlates symmetry to the ionic size and the electron Accepted 19th June 2020 affinity of the central cation, X+. Providing an improved understanding of the fundamental factors DOI: 10.1039/d0sc02076a Creative Commons Attribution 3.0 Unported Licence. determining bond symmetry on a comprehensive level is expected to facilitate future developments and rsc.li/chemical-science applications of secondary bonding and hypervalent chemistry.
    [Show full text]
  • Surface Properties and Morphology of Boron Carbide Nanopowders Obtained by Lyophilization of Saccharide Precursors
    materials Article Surface Properties and Morphology of Boron Carbide Nanopowders Obtained by Lyophilization of Saccharide Precursors Dawid Kozie ´n 1,* , Piotr Jele ´n 1 , Joanna St˛epie´n 2 , Zbigniew Olejniczak 3 , Maciej Sitarz 1 and Zbigniew P˛edzich 1,* 1 Faculty of Materials Science and Ceramics, AGH University of Science and Technology, 30 Mickiewicz Av., 30-059 Kraków, Poland; [email protected] (P.J.); [email protected] (M.S.) 2 Academic Centre for Materials and Nanotechnology, AGH University of Science and Technology, 30 Mickiewicz Av., 30-059 Kraków, Poland; [email protected] 3 Institute of Nuclear Physics, 152 Radzikowskiego St., 31-342 Kraków, Poland; [email protected] * Correspondence: [email protected] (D.K.); [email protected] (Z.P.) Abstract: The powders of boron carbide are usually synthesized by the carbothermal reduction of boron oxide. As an alternative to high-temperature reactions, the development of the carbothermal reduction of organic precursors to produce B4C is receiving considerable interest. The aim of this work was to compare two methods of preparing different saccharide precursors mixed with boric acid with a molar ratio of boron to carbon of 1:9 for the synthesis of B4C. In the first method, aqueous ◦ ◦ solutions of saccharides and boric acid were dried overnight at 90 C and pyrolyzed at 850 C for 1 h under argon flow. In the second method, aqueous solutions of different saccharides and boric acid Citation: Kozie´n,D.; Jele´n,P.; were freeze-dried and prepared in the same way as in the first method.
    [Show full text]
  • Materials Design and Band Gap Engineering of Complex
    University of Louisville ThinkIR: The University of Louisville's Institutional Repository Electronic Theses and Dissertations 8-2016 Materials design and band gap engineering of complex nanostructures using a semi-empirical approach : low dimensional boron nanostructures, h-BN sheet with graphene domains and holey graphene. Cherno Baba Kah Follow this and additional works at: https://ir.library.louisville.edu/etd Part of the Condensed Matter Physics Commons Recommended Citation Kah, Cherno Baba, "Materials design and band gap engineering of complex nanostructures using a semi- empirical approach : low dimensional boron nanostructures, h-BN sheet with graphene domains and holey graphene." (2016). Electronic Theses and Dissertations. Paper 2491. https://doi.org/10.18297/etd/2491 This Doctoral Dissertation is brought to you for free and open access by ThinkIR: The University of Louisville's Institutional Repository. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of ThinkIR: The University of Louisville's Institutional Repository. This title appears here courtesy of the author, who has retained all other copyrights. For more information, please contact [email protected]. MATERIALS DESIGN AND BAND GAP ENGINEERING OF COMPLEX : LOW NANOSTRUCTURES USING A SEMI-EMPIRICAL APPROACH , h DIMENSIONAL BORON NANOSTRUCTURES - BN SHEET WITH GRAPHENE DOMAINS AND HOLEY GRAPHENE By Cherno Baba Kah M.S, University of Louisville, 2013 M.S, Clark Atlanta University, 2011 B.S, University of The Gambia,
    [Show full text]
  • Basic Concepts of Chemical Bonding
    Basic Concepts of Chemical Bonding Cover 8.1 to 8.7 EXCEPT 1. Omit Energetics of Ionic Bond Formation Omit Born-Haber Cycle 2. Omit Dipole Moments ELEMENTS & COMPOUNDS • Why do elements react to form compounds ? • What are the forces that hold atoms together in molecules ? and ions in ionic compounds ? Electron configuration predict reactivity Element Electron configurations Mg (12e) 1S 2 2S 2 2P 6 3S 2 Reactive Mg 2+ (10e) [Ne] Stable Cl(17e) 1S 2 2S 2 2P 6 3S 2 3P 5 Reactive Cl - (18e) [Ar] Stable CHEMICAL BONDSBONDS attractive force holding atoms together Single Bond : involves an electron pair e.g. H 2 Double Bond : involves two electron pairs e.g. O 2 Triple Bond : involves three electron pairs e.g. N 2 TYPES OF CHEMICAL BONDSBONDS Ionic Polar Covalent Two Extremes Covalent The Two Extremes IONIC BOND results from the transfer of electrons from a metal to a nonmetal. COVALENT BOND results from the sharing of electrons between the atoms. Usually found between nonmetals. The POLAR COVALENT bond is In-between • the IONIC BOND [ transfer of electrons ] and • the COVALENT BOND [ shared electrons] The pair of electrons in a polar covalent bond are not shared equally . DISCRIPTION OF ELECTRONS 1. How Many Electrons ? 2. Electron Configuration 3. Orbital Diagram 4. Quantum Numbers 5. LEWISLEWIS SYMBOLSSYMBOLS LEWISLEWIS SYMBOLSSYMBOLS 1. Electrons are represented as DOTS 2. Only VALENCE electrons are used Atomic Hydrogen is H • Atomic Lithium is Li • Atomic Sodium is Na • All of Group 1 has only one dot The Octet Rule Atoms gain, lose, or share electrons until they are surrounded by 8 valence electrons (s2 p6 ) All noble gases [EXCEPT HE] have s2 p6 configuration.
    [Show full text]
  • Organometrallic Chemistry
    CHE 425: ORGANOMETALLIC CHEMISTRY SOURCE: OPEN ACCESS FROM INTERNET; Striver and Atkins Inorganic Chemistry Lecturer: Prof. O. G. Adeyemi ORGANOMETALLIC CHEMISTRY Definitions: Organometallic compounds are compounds that possess one or more metal-carbon bond. The bond must be “ionic or covalent, localized or delocalized between one or more carbon atoms of an organic group or molecule and a transition, lanthanide, actinide, or main group metal atom.” Organometallic chemistry is often described as a bridge between organic and inorganic chemistry. Organometallic compounds are very important in the chemical industry, as a number of them are used as industrial catalysts and as a route to synthesizing drugs that would not have been possible using purely organic synthetic routes. Coordinative unsaturation is a term used to describe a complex that has one or more open coordination sites where another ligand can be accommodated. Coordinative unsaturation is a very important concept in organotrasition metal chemistry. Hapticity of a ligand is the number of atoms that are directly bonded to the metal centre. Hapticity is denoted with a Greek letter η (eta) and the number of bonds a ligand has with a metal centre is indicated as a superscript, thus η1, η2, η3, ηn for hapticity 1, 2, 3, and n respectively. Bridging ligands are normally preceded by μ, with a subscript to indicate the number of metal centres it bridges, e.g. μ2–CO for a CO that bridges two metal centres. Ambidentate ligands are polydentate ligands that can coordinate to the metal centre through one or more atoms. – – – For example CN can coordinate via C or N; SCN via S or N; NO2 via N or N.
    [Show full text]
  • Understanding the Invisible Hands of Sample Preparation for Cryo-EM
    FOCUS | REVIEW ARTICLE FOCUS | REVIEWhttps://doi.org/10.1038/s41592-021-01130-6 ARTICLE Understanding the invisible hands of sample preparation for cryo-EM Giulia Weissenberger1,2,3, Rene J. M. Henderikx1,2,3 and Peter J. Peters 2 ✉ Cryo-electron microscopy (cryo-EM) is rapidly becoming an attractive method in the field of structural biology. With the exploding popularity of cryo-EM, sample preparation must evolve to prevent congestion in the workflow. The dire need for improved microscopy samples has led to a diversification of methods. This Review aims to categorize and explain the principles behind various techniques in the preparation of vitrified samples for the electron microscope. Various aspects and challenges in the workflow are discussed, from sample optimization and carriers to deposition and vitrification. Reliable and versatile specimen preparation remains a challenge, and we hope to give guidelines and posit future directions for improvement. ryo-EM is providing macromolecular structures with the optimum biochemical state of the sample. Grid preparation up to atomic resolution at an unprecedented rate. In this describes the steps needed to make a sample suitable for analysis Ctechnique, electron microscopy images of biomolecules in the microscope. These steps involve chemical or plasma treat- embedded in vitreous, glass-like ice are combined to generate ment of the grid, sample deposition and vitrification. The first three-dimensional (3D) reconstructions. The detailed structural breakthroughs came about from a manual blot-and-plunge method models obtained from these reconstructions grant insight into the developed in the 1980s15 that is still being applied to achieve formi- function of macromole cules and their role in biological processes.
    [Show full text]
  • 18- Electron Rule. 18 Electron Rule Cont’D Recall That for MAIN GROUP Elements the Octet Rule Is Used to Predict the Formulae of Covalent Compounds
    18- Electron Rule. 18 Electron Rule cont’d Recall that for MAIN GROUP elements the octet rule is used to predict the formulae of covalent compounds. Example 1. This rule assumes that the central atom in a compound will make bonds such Oxidation state of Co? [Co(NH ) ]+3 that the total number of electrons around the central atom is 8. THIS IS THE 3 6 Electron configuration of Co? MAXIMUM CAPACITY OF THE s and p orbitals. Electrons from Ligands? Electrons from Co? This rule is only valid for Total electrons? Period 2 nonmetallic elements. Example 2. Oxidation state of Fe? The 18-electron Rule is based on a similar concept. Electron configuration of Fe? [Fe(CO) ] The central TM can accommodate electrons in the s, p, and d orbitals. 5 Electrons from Ligands? Electrons from Fe? s (2) , p (6) , and d (10) = maximum of 18 Total electrons? This means that a TM can add electrons from Lewis Bases (or ligands) in What can the EAN rule tell us about [Fe(CO)5]? addition to its valence electrons to a total of 18. It can’t occur…… 20-electron complex. This is also known Effective Atomic Number (EAN) Rule Note that it only applies to metals with low oxidation states. 1 2 Sandwich Compounds Obeying EAN EAN Summary 1. Works well only for d-block metals. It does not apply to f-block Let’s draw some structures and see some new ligands. metals. 2. Works best for compounds with TMs of low ox. state. Each of these ligands is π-bonded above and below the metal center.
    [Show full text]