DOCSLIB.ORG

A Statistical Performance Model of the Opteron Processor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Statistical Performance Model of the Opteron Processor A Statistical Performance Model of the Opteron Processor Jeanine Cook Jonathan Cook Waleed Alkohlani New Mexico State University New Mexico State University New Mexico State University Klipsch School of Electrical Department of Computer Klipsch School of Electrical and Computer Engineering Science and Computer Engineering [email protected] [email protected] [email protected] ABSTRACT m5 [11], Simics/GEMS [25], and more recently MARSSx86 [5]{ Cycle-accurate simulation is the dominant methodology for the only one supporting the popular x86 architecture. Some processor design space analysis and performance prediction. of these have not been validated against real hardware in However, with the prevalence of multi-core, multi-threaded the multi-core mode (SESC and M5), and the others that architectures, this method has become highly impractical as are validated show large errors of up to 50% [5]. All cycle- the sole means for design due to its extreme slowdowns. We accurate multi-core simulators are very slow; a few hundred have developed a statistical technique for modeling multi- thousand simulated instructions per second is the most op- core processors that is based on Monte Carlo methods. Us- timistic speed with the help of native mode execution. Fur- ing this method, processor models of contemporary archi- ther, the architectures supported by many of these simula- tectures can be developed and applied to performance pre- tors are now obsolete. diction, bottleneck detection, and limited design space anal- ysis. To date, we have accurately modeled the IBM Cell, the To address these issues and to satisfy our own desire for Intel Itanium, and the Sun Niagara 1 and Niagara 2 proces- performance models of contemporary processors, we devel- sors [34, 33, 10]. In this paper, we present a work in progress oped a statistical modeling technique based on Monte Carlo which is applying this methodology to an out-of-order exe- methods that we believe can be applied to in-order and out- cution processor. We present the initial single-core model of-order execution, multi-core processors. We introduced and results for the AMD Barcelona (Opteron) processor. this method in [34, 33]; the method was presented in detail using the Niagara 2 model as an example in [10]. These 1. INTRODUCTION previous models were all of in-order execution processors. The complexity of contemporary processor architectures in The model presented here of the Opteron is the first we are combination with the large slowdowns of cycle-accurate sim- developing for an out-of-order execution architecture. ulators has given rise to the need for alternate performance analysis and prediction techniques that enable faster analy- Monte Carlo methods are a class of algorithms that rely on sis and identification of performance bottlenecks. As noted repeated random sampling to compute a result. Our pro- recently in a panel discussion on computer architecture re- cessor modeling technique probabilistically represents the search directions, \Intel cycle-accurate performance simula- executed instruction stream and randomly samples several tors currently run at roughly 10 thousand instructions per histograms that are related to stall conditions. Instructions second (KIPS) when simulating a unicore processor. At 10 proceed to specific delay centers (e.g., execution units, cache, KIPS, it will take more than nine days to simulate 1 second memory) based on probabilities. Cycles are counted for each of the eight-way multicore processor execution. Things will instruction according to the stall conditions and the latency only get worse as the number of simulated cores grows." [17]. of the specific delay center that executes the instruction. This time perturbation makes simulating a realistic work- The model converges and produces a result when it reaches load unrealistic! a threshold based on the difference in CPI between consec- utive intervals of a pre-defined size. All of the in-order exe- Another motivation for alternate performance analysis tech- cution models converge within seconds; the current Opteron niques is the lack of availability of simulators for modern model usually converges within seconds, but for some appli- multi-core architectures. A limited number of academically- cations, convergence takes minutes. available cycle-accurate simulators have various levels of multi- core simulation support, the most popular being SESC [31], New processor models using the Monte Carlo modeling tech- nique can be developed quickly. A basic model can be cre- ated in a few months; validating and re-developing for better accuracy takes another few months. The newer models (Ni- agara and Opteron) are coded in C++; the older models are written in C. The Opteron model is the largest at ap- proximately 2000 lines of code; all of the other models are implemented in hundreds of lines. In this paper, we present the initial Monte Carlo single-core processor model that we are developing for the Opteron, to extract a particular latency or to study a specific behav- Barcelona architecture. The Barcelona is a Family 10h ar- ior or micro-architecture feature. The data dependence his- chitecture; we model the micro-architecture core of Family tograms are sampled by the model to determine the latency 10h processors. We extended the methodology to enable of subsequent dependent instructions. modeling of out-of-order execution, which represents a sig- nificant extension in comparison to prior models with respect Data dependence information is collected according to which to the micro-architecture components modeled and overall type of data hazards can occur in the micro-architecture: model complexity. The Opteron model is parameterized and read-after-write (RAW), write-after-write (WAW), and write- generalized so that it is not just an attempt to model an ex- after-read (WAR). WAW and WAR hazards are typically re- isting processor, but can be configured to understand the solved through register renaming. Therefore, in most mod- performance tradeoffs when alternatives are evaluated. els, only true dependences (RAW) need to be accounted for. Our effort is not yet complete but is producing initial results. The data dependence information is represented as a dis- In this paper we present initial performance prediction re- tance in number of instructions between the operand pro- sults. Although we have performed some initial validation ducing and operand consuming instructions. For example, and model refinement, we are still working on areas where the distance between the producing and consuming instruc- the model is inaccurate, mostly due to iteratively under- tion in the following sequence is 3. standing the details of available documentation as they per- ldub [%i4 + %i2]; %i0 tain to actual processor behavior. The results are not final nop and, from experience, are expected to improve as validation nop is completed. or %i0; 2; %i0 2. MONTE CARLO PROCESSOR MODEL- These dependence distances are collected over the entire dy- ING (MCPM) TECHNIQUE namic execution of an application and are used to produce The Monte Carlo modeling methodology is a technique that a histogram. For the Opteron model, a histogram is gener- statistically models processor behavior and predicts the per- ated for each executed instruction; the histogram contains a formance of contemporary, single- and multi-core processors. distribution of the number of dynamic instructions that sep- Our statistical modeling technique is based on the Monte arate the producing instruction (e.g.,movq %rax, -8(%rbp)) Carlo method and uses both dynamic application and pro- and its consumer. Figure 1 shows the MOV64-to-use his- cessor characteristics as parameters to the model. Models are developed based on a particular existing processor and can subsequently be modified to model a different processor 4E+09 in the same family. 3.5E+09 3E+09 The models predict CPI (cycles per instruction) and use the equation: 2.5E+09 2E+09 CPI = CPIi + CPIs (1) 1.5E+09 # of Instrucons where CPIi is the intrinsic or ideal CPI based on the issue 1E+09 width, and CPI is the CPI due to stalls. The cause of s 500000000 stalls depends on the micro-architecture; data dependences, branch mis-predictions, and cache misses are stall causes 0 common to many processors. Stalls due to a full reorder 1 3 5 7 9 11 13 15 17 19 21 23 25 buffer, full reservation stations, and full scheduling queues Distance are also common in out-of-order execution processors. Once stall causes are identified, we collect data on their frequency using on-chip performance counters (branch mis-predictions, Figure 1: MOV64-to-use Histogram, astar cache misses, TLB misses) and binary instrumentation tools (data dependences). The cache and transition lookaside togram for the SPEC CPU2006 [4] INT benchmark, astar . buffer (TLB) hit/miss data is used to probabilistically deter- The figure shows that the instruction dependent on a pro- mine (realized as a transition probability) where in the cache ducing mov instruction will most likely be 4, 2, or 3 instruc- hierarchy a memory reference instruction is satisfied. The tions, respectively, following the producing instruction. branch mis-prediction rate is used to statistically determine whether a branch is predicted correctly or not. The dynamic instruction mix and any data associated with variable latency micro-architecture components is collected Latency characteristics for various processor components such using binary instrumentation. The instruction mix is used as caches, execution units (EUs), and branch predictors are to generate an instruction stream for the model that sta- also used in the model. These are primarily obtained from tistically represents the instruction stream generated by the the processor hardware manual and verified using micro- application. benchmarks. In cases where latencies are not given in the manual or when component latencies are variable, we use Monte Carlo processor models converge to a predicted CPI targeted micro-benchmarks to determine these numbers. Tar- based on a pre-defined threshold value.
Load more

Recommended publications
  • Mairjason2015phd.Pdf (1.650Mb)
    Power Modelling in Multicore Computing Jason Mair a thesis submitted for the degree of Doctor of Philosophy at the University of Otago, Dunedin, New Zealand. 2015 Abstract Power consumption has long been a concern for portable consumer electron- ics, but has recently become an increasing concern for larger, power-hungry systems such as servers and clusters. This concern has arisen from the asso- ciated financial cost and environmental impact, where the cost of powering and cooling a large-scale system deployment can be on the order of mil- lions of dollars a year. Such a substantial power consumption additionally contributes significant levels of greenhouse gas emissions. Therefore, software-based power management policies have been used to more effectively manage a system’s power consumption. However, man- aging power consumption requires fine-grained power values for evaluating the run-time tradeoff between power and performance. Despite hardware power meters providing a convenient and accurate source of power val- ues, they are incapable of providing the fine-grained, per-application power measurements required in power management. To meet this challenge, this thesis proposes a novel power modelling method called W-Classifier. In this method, a parameterised micro-benchmark is designed to reproduce a selection of representative, synthetic workloads for quantifying the relationship between key performance events and the cor- responding power values. Using the micro-benchmark enables W-Classifier to be application independent, which is a novel feature of the method. To improve accuracy, W-Classifier uses run-time workload classification and derives a collection of workload-specific linear functions for power estima- tion, which is another novel feature for power modelling.
    [Show full text]
  • Power Modeling
    CHAPTER 5 POWER MODELING Jason Mair1, Zhiyi Huang1, David Eyers1, Leandro Cupertino2, Georges Da Costa2, Jean-Marc Pierson2 and Helmut Hlavacs3 1Department of Computer Science, University of Otago, New Zealand 2Institute for Research in Informatics of Toulouse (IRIT), University of Toulouse III, France 3Faculty of Computer Science, University of Vienna, Austria 5.1 Introduction Power consumption has long been a concern for portable consumer electronics, with many manufacturers explicitly seeking to maximize battery life in order to improve the usability of devices such as laptops and smart phones. However, it has recently become a concern in the domain of much larger, more power hungry systems such as servers, clusters and data centers. This new drive to improve energy efficiency is in part due to the increasing deployment of large-scale systems in more businesses and industries, which have two pri- mary motives for saving energy. Firstly, there is the traditional economic incentive for a business to reduce their operating costs, where the cost of powering and cooling a large data center can be on the order of millions of dollars [18]. Reducing the total cost of own- ership for servers could help to stimulate further deployments. As servers become more affordable, deployments will increase in businesses where concerns over lifetime costs pre- viously prevented adoption. The second motivating factor is the increasing awareness of the environmental impact—e.g. greenhouse gas emissions—caused by power production. Reducing energy consumption can help a business indirectly reduce their environmental impact, making them more clean and green. The most commonly adopted solution for reducing power consumption is a hardware- based approach, where old, inefficient hardware is replaced with newer, more energy effi- COST Action 0804, edition.
    [Show full text]
  • Contributions of Hybrid Architectures to Depth Imaging: a CPU, APU and GPU Comparative Study
    Contributions of hybrid architectures to depth imaging : a CPU, APU and GPU comparative study Issam Said To cite this version: Issam Said. Contributions of hybrid architectures to depth imaging : a CPU, APU and GPU com- parative study. Hardware Architecture [cs.AR]. Université Pierre et Marie Curie - Paris VI, 2015. English. NNT : 2015PA066531. tel-01248522v2 HAL Id: tel-01248522 https://tel.archives-ouvertes.fr/tel-01248522v2 Submitted on 20 May 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THESE` DE DOCTORAT DE l’UNIVERSITE´ PIERRE ET MARIE CURIE sp´ecialit´e Informatique Ecole´ doctorale Informatique, T´el´ecommunications et Electronique´ (Paris) pr´esent´eeet soutenue publiquement par Issam SAID pour obtenir le grade de DOCTEUR en SCIENCES de l’UNIVERSITE´ PIERRE ET MARIE CURIE Apports des architectures hybrides `a l’imagerie profondeur : ´etude comparative entre CPU, APU et GPU Th`esedirig´eepar Jean-Luc Lamotte et Pierre Fortin soutenue le Lundi 21 D´ecembre 2015 apr`es avis des rapporteurs M. Fran¸cois Bodin Professeur, Universit´ede Rennes 1 M. Christophe Calvin Chef de projet, CEA devant le jury compos´ede M. Fran¸cois Bodin Professeur, Universit´ede Rennes 1 M.
    [Show full text]
  • AMD's Early Processor Lines, up to the Hammer Family (Families K8
    AMD’s early processor lines, up to the Hammer Family (Families K8 - K10.5h) Dezső Sima October 2018 (Ver. 1.1) Sima Dezső, 2018 AMD’s early processor lines, up to the Hammer Family (Families K8 - K10.5h) • 1. Introduction to AMD’s processor families • 2. AMD’s 32-bit x86 families • 3. Migration of 32-bit ISAs and microarchitectures to 64-bit • 4. Overview of AMD’s K8 – K10.5 (Hammer-based) families • 5. The K8 (Hammer) family • 6. The K10 Barcelona family • 7. The K10.5 Shanghai family • 8. The K10.5 Istambul family • 9. The K10.5-based Magny-Course/Lisbon family • 10. References 1. Introduction to AMD’s processor families 1. Introduction to AMD’s processor families (1) 1. Introduction to AMD’s processor families AMD’s early x86 processor history [1] AMD’s own processors Second sourced processors 1. Introduction to AMD’s processor families (2) Evolution of AMD’s early processors [2] 1. Introduction to AMD’s processor families (3) Historical remarks 1) Beyond x86 processors AMD also designed and marketed two embedded processor families; • the 2900 family of bipolar, 4-bit slice microprocessors (1975-?) used in a number of processors, such as particular DEC 11 family models, and • the 29000 family (29K family) of CMOS, 32-bit embedded microcontrollers (1987-95). In late 1995 AMD cancelled their 29K family development and transferred the related design team to the firm’s K5 effort, in order to focus on x86 processors [3]. 2) Initially, AMD designed the Am386/486 processors that were clones of Intel’s processors.
    [Show full text]
  • The Severest of Them All: Inference Attacks Against Secure Virtual Enclaves Jan Werner Joshua Mason Manos Antonakakis UNC Chapel Hill U
    The SEVerESt Of Them All: Inference Attacks Against Secure Virtual Enclaves Jan Werner Joshua Mason Manos Antonakakis UNC Chapel Hill U. Illinois Georgia Tech [email protected] [email protected] [email protected] Michalis Polychronakis Fabian Monrose Stony Brook University UNC Chapel Hill [email protected] [email protected] ABSTRACT and Communications Security (AsiaCCS ’19), July 9–12, 2019, Auckland, The success of cloud computing has shown that the cost and con- New Zealand. ACM, New York, NY, USA, 13 pages. https://doi.org/10.1145/ venience benefits of outsourcing infrastructure, platform, and soft- 3321705.3329820 ware resources outweigh concerns about confidentiality. Still, many businesses resist moving private data to cloud providers due to in- 1 INTRODUCTION tellectual property and privacy reasons. A recent wave of hardware Of late, the need for a Trusted Execution Environment has risen virtualization technologies aims to alleviate these concerns by of- to the forefront as an important consideration for many parties in fering encrypted virtualization features that support data confiden- the cloud computing ecosystem. Cloud computing refers to the use tiality of guest virtual machines (e.g., by transparently encrypting of on-demand networked infrastructure software and capacity to memory) even when running on top untrusted hypervisors. provide resources to customers [52]. In today’s marketplace, con- We introduce two new attacks that can breach the confidentiality tent providers desire the ability to deliver copyrighted or sensitive of protected enclaves. First, we show how a cloud adversary can material to clients without the risk of data leaks. At the same time, judiciously inspect the general purpose registers to unmask the computer manufacturers must be able to verify that only trusted computation that passes through them.
    [Show full text]
  • Windows 8 Is the Codename for the Next Version of the Microsoft Windows Computer Operating System Following Windows 7. It Has Ma
    Windows 8 is the codename for the next version of the Microsoft Windows computer operating system following Windows 7.[3] It has many changes from previous versions. In particular it adds support for ARM microprocessors in addition to the previously supported x86 microprocessors from Intel and AMD. A new Metro-style interface has been added that was designed fortouchscreen input in addition to mouse, keyboard, and pen input. Its server version is codenamed Windows Server 8. It will be released in late 2012. Early announcements In January 2011, at the Consumer Electronics Show (CES), Microsoft announced that Windows 8 would be adding support forARM microprocessors in addition to the x86 microprocessors from Intel and AMD.[4][5] [edit]Milestone leaks . A 32-bit Milestone 1 build, build 7850, with a build date of September 22, 2010, was leaked to BetaArchive, an online beta community, and to P2P/torrent sharing networks as well on April 12, 2011.[6] Milestone 1 includes a ribbon interface for Windows Explorer,[7] a PDF reader called Modern Reader, an updated task manager called Modern Task Manager,[8] and native ISO image mounting.[9] . A 32-bit Milestone 2 build, build 7927, was leaked to The Pirate Bay on August 29, 2011[10] right after many pictures leaked on BetaArchive the day before.[11] Features of this build are mostly the same as build 7955.[12] . A 32-bit Milestone 2 build, build 7955, was leaked to BetaArchive on April 25, 2011.[13] Features of this build included a new pattern login and a new file system known as Protogon, which is now known as ReFS and only included in server versions.[14] .
    [Show full text]
  • What Every Programmer Should Know About Memory
    What Every Programmer Should Know About Memory Ulrich Drepper Red Hat, Inc. [email protected] November 21, 2007 Abstract As CPU cores become both faster and more numerous, the limiting factor for most programs is now, and will be for some time, memory access. Hardware designers have come up with ever more sophisticated memory handling and acceleration techniques–such as CPU caches–but these cannot work optimally without some help from the programmer. Unfortunately, neither the structure nor the cost of using the memory subsystem of a computer or the caches on CPUs is well understood by most programmers. This paper explains the structure of memory subsys- tems in use on modern commodity hardware, illustrating why CPU caches were developed, how they work, and what programs should do to achieve optimal performance by utilizing them. 1 Introduction day these changes mainly come in the following forms: In the early days computers were much simpler. The var- • RAM hardware design (speed and parallelism). ious components of a system, such as the CPU, memory, mass storage, and network interfaces, were developed to- • Memory controller designs. gether and, as a result, were quite balanced in their per- • CPU caches. formance. For example, the memory and network inter- faces were not (much) faster than the CPU at providing • Direct memory access (DMA) for devices. data. This situation changed once the basic structure of com- For the most part, this document will deal with CPU puters stabilized and hardware developers concentrated caches and some effects of memory controller design. on optimizing individual subsystems. Suddenly the per- In the process of exploring these topics, we will explore formance of some components of the computer fell sig- DMA and bring it into the larger picture.
    [Show full text]
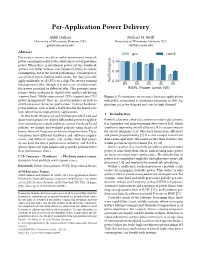
  • Per-Application Power Delivery
    Per-Application Power Delivery Akhil Guliani Michael M. Swift University of Wisconsin-Madison, USA University of Wisconsin-Madison, USA [email protected] [email protected] Abstract Datacenter servers are often under-provisioned for peak power consumption due to the substantial cost of providing power. When there is insufficient power for the workload, servers can lower voltage and frequency levels to reduce consumption, but at the cost of performance. Current proces- sors provide power limiting mechanisms, but they generally apply uniformly to all CPUs on a chip. For servers running heterogeneous jobs, though, it is necessary to differentiate the power provided to different jobs. This prevents inter- ference when a job may be throttled by another job hitting a power limit. While some recent CPUs support per-CPU Figure 1. Performance interference between applications power management, there are no clear policies on how to with RAPL, normalized to standalone execution at 85W. Ap- distribute power between applications. Current hardware plication gcc is low demand and cam4 is high demand. power limiters, such as Intel’s RAPL throttle the fastest core first, which harms high-priority applications. In this work, we propose and evaluate priority-based and 1 Introduction share-based policies to deliver differential power to applica- Power has become a first-class citizen in modern data centers: tions executing on a single socket in a server. For share-based it is a primary cost in provisioning data centers [16], which policies, we design and evaluate policies using shares of emphasize improving overall efficiency. It is a major concern power, shares of frequency, and shares of performance.
    [Show full text]
  • A Comparative Study of 64 Bit Microprocessors Apple, Intel and AMD
    Special Issue - 2016 International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 ICACT - 2016 Conference Proceedings A Comparative Study of 64 Bit Microprocessors Apple, Intel and AMD Surakshitha S Shifa A Ameen Rekha P M Information Science and Engineering Information Science and Engineering Information Science and Engineering JSSATE JSSATE JSSATE Bangalore, India Bangalore, India Bangalore, India Abstract- In this paper, we draw a comparative study of registers, even larger .The term may also refer to the size of microprocessor, using the three major processors; Apple, low-level data types, such as 64-bit floating-point numbers. Intel and AMD. Although the philosophy of their micro Most CPUs are designed so that the contents of a architecture is the same, they differ in their approaches to single integer register can store the address of any data in implementation. We discuss architecture issues, limitations, the computer's virtual considered an appropriate size to architectures and their features .We live in a world of constant competition dating to the historical words of the work with for another important reason: 4.29 billion Charles Darwin-‘Survival of the fittest ‘. As time passed by, integers are enough to assign unique references to most applications needed more processing power and this lead to entities in applications like databases. an explosive era of research on the architecture of Some supercomputer architectures of the 1970s and microprocessors. We present a technical & comparative study 1980s used registers up to 64 bits wide. In the mid-1980s, of these smart microprocessors. We study and compare two Intel i860 development began culminating in a 1989 microprocessor families that have been at the core of the release.
    [Show full text]
  • Pomiary Efektywności Dla AMD Family 10H
    Pomiary efektywności dla AMD Family 10h Na podstawie dokumentacji AMD opracował: Rafał Walkowiak Wersja wrzesień 2016 Liczniki zdarzeń a program profilujący • Procesory AMD 10h wyposażone są w 4 liczniki wydajności przeznaczone do zliczania zdarzeń (w badanym okresie) spowodowanych przez aplikacje użytkownika i system operacyjny: liczba cykli CPU, liczba zatwierdzonych instrukcji, braków trafień do pp i podobnych zdarzeń. • Program profilujący konfiguruje liczniki - określa jakie zdarzenie oraz przy jakich warunkach dodatkowych ma być zliczane i badane. Pomiary efektywności dla AMD Family 10h 2 Metody pomiaru wydajności • Podejście klamrowe (ang. caliper mode) – odczyt wartości licznika zdarzeń przed wejściem i po zakończeniu przetwarzania w krytycznym efektywnościowo fragmencie kodu. W wyniku odjęcia wartość zmierzonej „po” od wartości zmierzonej „przed” uzyskujemy liczbę zdarzeń za których wystąpienie odpowiedzialny jest testowany kod. W podejściu tym: • nie ma możliwości pomiaru dystrybucji mierzonych zdarzeń w badanym obszarze, • nie ma możliwości powiązania wystąpienia zdarzenia z powodującą je instrukcją – NIE WIADOMO JAKA PRZYCZYNA ZDARZENIA • Podejście próbkowania wg licznika wydajności – licznik wydajności ładowany jest wartością limitu lub progu. Zliczenie określonej w ten sposób liczby zdarzeń powoduje wywołanie procedury przerwania dla obsługi zdarzenia, która zapisuje: – typ zdarzenia, ID procesu, ID wątku i IP – ZNANY LICZNIK INSTRUKCJI W OKOLICY instrukcji BĘDĄCEJ PRZYCZYNĄ ZDARZENIA. Pomiary efektywności dla AMD Family
    [Show full text]
  • Open-Source Register Reference for AMD Family 17H Processors Models 00H-2Fh
    56255 Rev 3.03 - July, 2018 OSRR for AMD Family 17h processors, Models 00h-2Fh Open-Source Register Reference For AMD Family 17h Processors Models 00h-2Fh 1 56255 Rev 3.03 - July, 2018 OSRR for AMD Family 17h processors, Models 00h-2Fh Legal Notices © 2017,2018 Advanced Micro Devices, Inc. All rights reserved. The information contained herein is for informational purposes only, and is subject to change without notice. While every precaution has been taken in the preparation of this document, it may contain technical inaccuracies, omissions and typographical errors, and AMD is under no obligation to update or otherwise correct this information. Advanced Micro Devices, Inc. makes no representations or warranties with respect to the accuracy or completeness of the contents of this document, and assumes no liability of any kind, including the implied warranties of noninfringement, merchantability or fitness for particular purposes, with respect to the operation or use of AMD hardware, software or other products described herein. No license, including implied or arising by estoppel, to any intellectual property rights is granted by this document. Terms and limitations applicable to the purchase or use of AMD’s products are as set forth in a signed agreement between the parties or in AMD's Standard Terms and Conditions of Sale. Trademarks: AMD, the AMD Arrow logo, and combinations thereof are trademarks of Advanced Micro Devices, Inc. 3DNow! is a trademark of Advanced Micro Devices, Incorporated. AGESA is a trademark of Advanced Micro Devices, Incorporated. AMD Virtualization is a trademark of Advanced Micro Devices, Incorporated. MMX is a trademark of Intel Corporation.
    [Show full text]
  • Position List Word Aligned Hybrid: Optimizing Space and Performance for Compressed Bitmaps
    Position List Word Aligned Hybrid: Optimizing Space and Performance for Compressed Bitmaps François Deliège Torben Bach Pedersen Department of Computer Science Department of Computer Science Aalborg University, Denmark Aalborg University, Denmark [email protected] [email protected] ABSTRACT then, various approaches have been studied to improve bitmap in- Compressed bitmap indexes are increasingly used for efficiently dexes for high-cardinality attributes. A deeper review of bitmap querying very large and complex databases. The Word Aligned index extensions, compression techniques, and technologies used Hybrid (WAH) bitmap compression scheme is commonly recog- in commercial DBMSes is presented in [15]. nized as the most efficient compression scheme in terms of CPU The binning technique partitions the values of the index attributes efficiency. However, WAH compressed bitmaps use a lot of stor- into ranges [13, 17]. Each bitmap captures a range of values rather age space. This paper presents the Position List Word Aligned than a single value. Binning techniques prove to be useful when Hybrid (PLWAH) compression scheme that improves significantly the attribute values can be partitioned into sets. In [8], a binning over WAH compression by better utilizing the available bits and technique using partitioning based on query patterns, their frequen- new CPU instructions. For typical bit distributions, PLWAH com- cies, and the data distribution is presented and further improves the pressed bitmaps are often half the size of WAH bitmaps and, at the index performance. Bit-slicing techniques rely on an ordered list same time, offer an even better CPU efficiency. The results are ver- of bitmaps [11]. If every value of an attribute can be represented ified by theoretical estimates and extensive experiments on large using n bits, then the indexed attribute is represented with an or- amounts of both synthetic and real-world data.
    [Show full text]