View Full Text-PDF
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

HŒ臬 A„簧綟糜恥sµ, Vw笑n® 22.12.2019 Š U拳 W
||Om Shri Manjunathaya Namah || Shri Kshethra Dhamasthala Rural Development Project B.C. Trust ® Head Office Dharmasthala HŒ¯å A„®ãtÁS®¢Sµ, vw¯ºN® 22.12.2019 Š®0u®± w®lµu® îµ±°ªæX¯Š®N®/ N®Zµ°‹ š®œ¯‡®±N®/w®S®u®± š®œ¯‡®±N® œ®±uµÛ‡®± wµ°Š® wµ°î®±N¯r‡®± ªRq® y®‹°£µ‡®± y®ªq¯ºý® D Nµ¡®w®ºruµ. Cu®Š®ªå 50 î®±q®±Ù 50 Oʺq® œµX®±Ï AºN® y®lµu®î®Š®w®±Ý (¬šµ¶g¬w®ªå r¢›Š®±î®ºqµ N®Zµ°‹/w®S®u®± š®œ¯‡®±N® œ®±uµÛSµ N®xÇ®Õ ïu¯ãœ®Áqµ y®u®ï î®±q®±Ù ®±š®±é 01.12.2019 NµÊ Aw®æ‡®±î¯S®±î®ºqµ 25 î®Ç®Á ï±°Š®u®ºqµ î®±q®±Ù îµ±ªæX¯Š®N® œ®±uµÛSµ N®xÇ®Õ Hš¬.Hš¬.HŒ¬.› /z.‡®±±.› ïu¯ãœ®Áqµ‡µ²ºvSµ 3 î®Ç®Áu® Nµ©š®u® Aw®±„Â®î® î®±q®±Ù ®±š®±é 01.12.2019 NµÊ Aw®æ‡®±î¯S®±î®ºqµ 30 î®Ç®Á ï±°Š®u®ºqµ ) î®±±ºvw® œ®ºq®u® š®ºu®ý®Áw®NµÊ B‡µ±Ê ¯l®Œ¯S®±î®¼u®±. š®ºu®ý®Áw®u® š®Ú¡® î®±q®±Ù vw¯ºN®î®w®±Ý y®äqµã°N®î¯T Hš¬.Hº.Hš¬ î®±²©N® ¯Ÿr x°l®Œ¯S®±î®¼u®±. œ¯cŠ¯u® HŒ¯å A„®ãtÁS®¢Sµ A†Ãw®ºu®wµS®¡®±. Written test Sl No Name Address Taluk District mark Exam Centre out off 100 11 th ward near police station 1 A Ashwini Hospete Bellary 33 Bellary kampli 2 Abbana Durugappa Nanyapura HB hally Bellary 53 Bellary 'Sri Devi Krupa ' B.S.N.L 2nd 3 Abha Shrutee stage, Near RTO, Satyamangala, Hassan Hassan 42 Hassan Hassan. -

Dist Name Taluk Name GP Name New Accoun No Bank Name
ANNEXURE Releases to Dharwar Dist Dist_name taluk_name GP_name New Accoun no Bank_name Branch name IFSC code rel_amount Dharwar Dharwad Arwatagi 5743 Karnataka Vikasa Grameena Bank (KVGB) ARWATAGI 1.00 Dharwar Dharwad Belur 135001010006162 Vijaya Bank KOTUR VIJD0001350 1.00 Dharwar Dharwad Benachi 5741 Karnataka Vikasa Grameena Bank (KVGB) ARWATAGI 2.00 Dharwar Dharwad Devarhubbali 9726 Karnataka Vikasa Grameena Bank (KVGB) NIGADI 3.00 Dharwar Dharwad Garag 11194 Indian Overseas Bank (IOB) GARAG IOBA0000308 1.00 Dharwar Dharwad Halligeri 9722 Karnataka Vikasa Grameena Bank (KVGB) NIGADI 2.00 Dharwar Dharwad Hangarki 11195 Indian Overseas Bank (IOB) GARAG IOBA0000308 2.00 Dharwar Dharwad Hebballi 841710100008076 Bank of India (BOI) HEBBALLI BKID0008417 5.00 Dharwar Dharwad Honnapur 5746 Karnataka Vikasa Grameena Bank (KVGB) ARWATAGI 5.00 Dharwar Dharwad Kalakeri 7347 Karnataka Vikasa Grameena Bank (KVGB) MUGAD 3.00 Dharwar Dharwad Kanakur 5572 Karnataka Vikasa Grameena Bank (KVGB) SHIVALLI 2.00 Dharwar Dharwad Kotabagi 11211 Indian Overseas Bank (IOB) GARAG IOBA0000308 2.00 Dharwar Dharwad Kotur 135001010006183 Vijaya Bank KOTUR VIJD0001350 3.00 Dharwar Dharwad Lokur 1692 Karnataka Vikasa Grameena Bank (KVGB) UPPIN BETAGERI 3.00 Dharwar Dharwad Madhanbhavi 8655 Karnataka Vikasa Grameena Bank (KVGB) TADAKOD 3.00 Dharwar Dharwad Managundi 137201010004389 Vijaya Bank HOSAYAL NAGAR DHARWAD VIJB0001372 3.00 Dharwar Dharwad Mandihal 7317 Karnataka Vikasa Grameena Bank (KVGB) MUGAD 4.00 Dharwar Dharwad Maradagi 5561 Karnataka Vikasa Grameena -

Fifth Research Council Meeting
UNIVERSITY OF AGRICULTURAL SCIENCES, DHARWAD FIFTH RESEARCH COUNCIL MEETING (Under UAS Act 2009) Venue: Conference Hall Date: 14-03-2017 Time: 11-00 am PROGRAMME Chairman : Dr. D.P. Biradar, Hon'ble Vice-Chancellor, UAS., Dharwad Dr. S.L.Madiwalar 1. Action Taken Report and Presentation of Research Activities/ Director of Research Achievements UAS, Dharwad 2. Discussion On Policy Issues Item Proposed by Moved by Director of Research Director of Research i) Ratification of Charging Fees for field inspection and issue of certificate to private companies Head of Department Dean (RHSc.) ii) Constitution of Institutional Research Ethical Committee Food Science & Nutrition 3. Any other item with the Permission of the Chair Person 4. Impressions of Expert Members 5. Remarks of Progressive Farmers 6. Wrap-up remarks by the Chairman 7. Vote of Thanks Dr. R. R. Patil Associate Director of Research (HQ) 1 C O N T E N T S Sl. Particulars Page No. No. 1. Action taken report on Suggestions of 4th 01 Research Council Meeting 2. Land Resource available in Research Stations 04 3. List of AICRP’s 07 4. Human Resource Engaged in Research 09 5. Budget Allocation for Research 10 6. Station wise Farm Receipts 13 7. Resource Mobilization through Adhoc Projects 14 8. Amount Realized through Testing trials 18 9. Staff Research Projects 19 10. Seed Production 20 11. Organic Inputs Production 28 12. List of MOU signed between UAS, Dharwad and 29 project funding agencies 13. Research Highlights 30 14. Rain fall and Temperature Variation in Recent Years 46 15. Technical Programme Implementation 48 16. -

K.L.E. INSTITUTE of TECHNOLOGY, HUBBALLI First Year Students
K. L. E. Society’s K.L.E. INSTITUTE OF TECHNOLOGY, HUBBALLI (AICTE approved, Affiliated to VTU and ISO 9001:2015 Certified) DEPARTMENT OF MECHANICAL ENGINEERING (NBA Accredited Program) Opposite Airport, Gokul, Hubballi-580027 Phone: 0836-2232664, Fax: 0836-2330688, E-mail: [email protected], website: www.kleit.ac.in First Year Students Roll USN Name of the Student No. 1 2KE19ME001 S ABDUL AZIZ 2 2KE19ME002 ABDULKHADAR RON 3 2KE19ME003 ABHISHEK ANEPPANAVAR 4 2KE19ME004 ABHISHEK JADHAV 5 2KE19ME005 ABHISHEK VISHWANATH KSHATRI 6 2KE19ME006 ADITYA TEMBE 7 2KE19ME007 AKASH S PATIL 8 2KE19ME009 AMBI MANDAR UTTAM 9 2KE19ME012 ANUP R CHAVAN 10 2KE19ME013 BALACHANDRA BHAT 11 2KE19ME014 BASAVARAJ HULIHALLI 12 2KE19ME015 BASAVRAJ S YATNALLI 13 2KE19ME016 CHAYA C PALANKAR 14 2KE19ME017 DARSHAN D MURDESHWAR 15 2KE19ME018 DAYASAGAR S HIREMATH 16 2KE19ME019 DEEPAK S NELLIKOPPA 17 2KE19ME020 FUAD AHMED KATNUR 18 2KE19ME021 H ABDUL AHAD 19 2KE19ME022 HARIF M JALADAGI 20 2KE19ME023 HRUTIK RAJU PARADDI 21 2KE19ME024 JUDERIN VIANNY DIAS 22 2KE19ME025 KARTHIK BASAVARAJ SANGOLLI K. L. E. Society’s K.L.E. INSTITUTE OF TECHNOLOGY, HUBBALLI (AICTE approved, Affiliated to VTU and ISO 9001:2015 Certified) DEPARTMENT OF MECHANICAL ENGINEERING (NBA Accredited Program) Opposite Airport, Gokul, Hubballi-580027 Phone: 0836-2232664, Fax: 0836-2330688, E-mail: [email protected], website: www.kleit.ac.in 23 2KE19ME026 KARTHIK M SHASHIMATH 24 2KE19ME027 KOUSTUBH NAMADEV RAYAMANE 25 2KE19ME028 KUMARAGOUDA N PATIL 26 2KE19ME029 KUSHALRAM M T 27 2KE19ME030 LAXMI R UKKALI -

List of Projects / Experiments (2013-14 & 2014-15)
UNIVERSITY OF AGRICULTURAL SCIENCES, DHARWAD LIST OF PROJECTS / EXPERIMENTS (2013-14 & 2014-15) UAS, Plan Grants GoK Staff Research RKVY Chemical & Hybrid Testing Research Projects Seed Production Directorate of Research, UAS, Dharwad C O N T E N T S Sl. No. Type of projects / experiments Page No. I. UAS Plan Grants 2-4 2013-14 & 2014-15 II. Government of Karnataka (GoK) 5 – 7 2013-14 & 2014-15 III. Rashtriya Krishi Vikas Yojane (RKVY) 8–10 2013-14 & 2014-15 IV. Staff Research 11– 19 2013-14 & 2014-15 V. Chemical & Hybrid Testing 20– 32 2013-14 VI. Adhoc Research Projects 33– 37 2013-14 & 2014-15 VII Seed Production 38 - 39 2013-14 & 2014-15 D:\Staff Code of DR UASD\N-Tech\PS (V. L. Shanbag)\Website Information 11-10-2013\Redesigning Website 03-05-2014\To be uploaded\List of projects - experiments.docx 1 I. UAS Plan Grants : D:\Staff Code of DR UASD\N-Tech\PS (V. L. Shanbag)\Website Information 11-10-2013\Redesigning Website 03-05-2014\To be uploaded\List of projects - experiments.docx 2 UAS, Plan Grants 2014-15(Continued Programme) Budget Sl. AB Scientists Title of the Projects (Rs. In No. A/c lakhs) Establishment of pesticide residue testing & 10.00 1. 6102 Dr. S. K. Gali quality analyses laboratory, UAS, Dharwad Dr. (Mrs.) O 0.10 2. 6118 Special innovative research programmes Sridevi Dr. Mamle Desai Agriculture information, business, export 3.21 3. 6168 wto -centre Dharwad Dr. (Mrs.) Geeta Commercialization of digital printing centre 2.87 4. 6148 Mahale by UAS, Dharwad. -

5 4 2 1 3 Division
Department of Public Instruction - Karnataka PROVISIONAL PRIORITY LIST FOR GHM/TGT/ SECONDARY TEACHER TRANSFER - 2016 (SECONDARY WITHIN UNIT ) DIVISION - BELGAUM Transfer Authority : JDPI - BELGAUM Priority No. Applicant Name School / Office Name DOB : DOJS Spouse Working/Residential Taluk Transfer Sought unit APPL No. Designation Subject DOEPSCHOOL : Spouse working/Residential district Counselling attending place DOEPCADRE DISE Code School / Office Name Working Taluk Name Gender/ Marital Prority Claimed status KGID No. School category / Working zone Working District/office Name Excess Teacher Completed years Total weightage Out of unit Transfer taken earlier and date CADRE GROUP - AM GROUP 1 BASAVARAJ GURULINGAPPA SAJJAN 20/07/1968 : 0 Within Unit 27/09/1997 113597 Assistant Master ( AM ) PCM KANNADA 25/03/2003 : - 0 BELGAUM 29030505112 GOVT HIGH SCHOOL JAMBAGI A VIJAYAPURA RURAL Male / Married TERMINALLY ILL CASES 1644333 Secondary / C VIJAYAPURA NO 18 36 - : - 2 ABDULHAMID FHARIDSAHEB HONNUTAGI 22/07/1969 : 0 Within Unit 06/07/2007 096812 TGT-SSA TGT - PCM - KANNADA 06/07/2007 : 0 BELGAUM 06/07/2007 29031200901 GOVT HPS ASANGIHAL SINDAGI Male / Married TERMINALLY ILL CASES 2220352 / C VIJAYAPURA NO 9 18 - : - 3 VISHWANATH S HIREMATH 14/02/1972 : 0 Within Unit 20/07/2007 014082 TGT-SSA TGT - PCM - KANNADA 20/07/2007 : 0 BELGAUM 20/07/2007 29090403001 HPS JIGALUR KUNDAGOL Male / Married TERMINALLY ILL CASES 2313490 / C DHARWAD NO 9 18 - : - 4 SHANKAR RAMASING JADHAV 01/06/1960 : 0 Within Unit 02/01/1981 032430 Assistant Master ( AM ) -

District Irrigation Plan (Dip)
DISTRICT IRRIGATION PLAN (DIP) UTTARAKANNADA DISTRICT KARNATAKA STATE 1 | D I P U K Index Sl no Contents Page NO 1 Introduction 6-7 Components and responsible Ministries /Departments 8-9 District Irrigation Plans (DIPs ) 10 Background 11 Vision and Objective 12 Strategy /Approach 13 Methodology 14 Rationale/Justification statement 15-16 2 CHAPTER -1 General Information district 1.1 District Profile 17 1.2 Brief History of the district 20-24 1.3 Present administrative Profile 24 1.4 Demography 25 1.5 Biomass and Livestock 27 1.6 Agro, Ecology, Climate, Hydrdogy, and topography 28-29 1.7 Land use pattern in uttarakannda 31 1.8 Soil Profile 35 1.9 Soil Erosion and Run off status 41 1.10 Rail Fall 42 1.11 Ground water 43 2 | D I P U K 3 CHAPTER -2 District water Profile 2.1 Area wise, Crop wise irrigation status 50 2.2 Production and productivity of major crops 53 2.3 Irrigation based classification 54 4 CHAPTER -3 3.1 Status of water availability 55 3.2 Status of ground water Availability 56 3.3 Existing type of irrigation 58 5 CHAPTER -4 Water Requirement demand 4.1 Domestic water 59 4.2 Crop water requirement 60 4.3 Livestock water demand 65 4.4 Industrials water demand 66 4.5 Water demand of power generation 67 4.6 Total water demand (Present) of district for various sectors 68 4.6 a Total water Demand of the District for various sectors 69 4.7 Water Budget 70 3 | D I P U K Index Sl no Contents (Table) Page No 1 1.1 District Profile 18 2 1.5 Biomass and Live stock 27 3 1.6 Agro, Ecology, Climate, Hydrology and topography 30 4 1.7 -
Sl. No. Roll No Name Mobile Category VH PH Subject` REF 1 15020128 JAGADESHA D 9739499799 CAT-IIIB NO NO KANNADA DU79675533 2 15
Sl. No. Roll No Name Mobile Category VH PH Subject` REF 1 15020128 JAGADESHA D 9739499799 CAT-IIIB NO NO KANNADA DU79675533 2 15030001 LAMBODAR CHANDRAKANT GAONKAR 7259980627 CAT-IIA NO NO ECONOMICS DU79186494 3 15010138 ANAND BASARAGI 8147087505 CAT-IIA NO NO COMMERCE DU79552467 4 15060002 NAGRAJ SAHDEV BELGAONKAR 9742436236 CAT-IIIB NO NO HISTORY DU79136956 5 15030007 CHEERANJEEVI KANNER 9916972682 ST NO NO ECONOMICS DU79077380 6 15020005 RAVI DEEVIGIHALLI 9845383596 ST NO NO KANNADA DU79078684 7 15090116 SOMANAT PUJAR 7829613973 SC NO NO HINDI DU79654339 8 15070031 SANTOSH KARAMALLAVAR 9916658271 CAT-IIIB NO YES SOCIOLOGY DU79526118 9 15040188 BASAVARAJ NAGALINGAPPA MALAGIHAL 9148928679 CAT-IIIB NO NO ENGLISH DU79759293 10 15250009 RAGHAVENDRA K SALI 9480774670 ST NO NO PHYSICAL SCIENCE DU79005835 11 15200122 DEMAPPA GOUDARA 7353466364 CAT-I NO NO PHYSICAL EDUCATION DU79802106 12 15380002 KOLI SHIVANAND HIRAGAPPA 9448627782 CAT-I NO NO Linguistics DU79208258 13 15040004 PARINITHA P 8277902771 CAT-IIIA NO NO English DU79052965 14 15010029 NAVEEN 9886881188 CAT-IIIA NO NO ACCOUNTING & TAXATION COMMERCE DU79082737 15 15050094 NAVEEN MARIGOUDAR 7259231516 CAT-IIIB NO NO POLITICAL SCIENCE DU79051286 16 15040632 PRAVEEN KURABAR S 8095102476 CAT-IIA NO NO ENGLISH DU80174218 17 15050002 ASHOK MADABHAVI 8105859120 CAT-IIA NO NO POLITICAL SCIENCE DU79074451 18 15280015 HATPAKKI APARNA JAYARAJ 9886907470 CAT-IIA NO NO BIOCHEMISTRY DU79006523 19 15270012 NIRANJANSWAMI SANGAYYA HIREMATH 8095703203 GEN NO NO CHEMISTRY DU79139002 20 15240006 SHRIDHAR -

Telephone Directory Also Available on UAS, Dharwad Website
Telephone Directory Also available on UAS, Dharwad website http://www.uasd.edu Directorate of Extension is maintain a Central Database on UAS, Dharwad Telephone Directory. Whenever there is a change in telephone numbers, designation, place of working, e-mails and fax numbers the same may please be communicated immediately to the Director of Extension, so as to update the information in the database. UNIVERSITY OF AGRICULTURAL SCIENCES, DHARWAD August, 2018 Telephone Directory UNIVERSITY OF AGRICULTURAL SCIENCES, DHARWAD Year of Publication : August, 2018 No. of Copies : 1000 No. Pages : XII+64 Compiled by : Dr. Sunil V. Halakatti Professor (Agri. Extension) & Technical Officer Directorate of Extension, UAS, Dharwad Dr. Smt. Geeta Chitagubbi Professor & Sr. Scientist (AICRP), HSc (FRM), UAS, Dharwad Editor : Dr. R. A. Balikai Publication Centre, Directorate of Education, UAS, Dharwad Published by : Dr. R. R. Patil Director of Extension, UAS, Dharwad Cover Page layout & : DTP Unit, Publication Centre Typesetting at UAS, Dharwad - 580 005 Cover page description : I. Administrative Building at Head Quarters II. Constituent Colleges of the University III. Major Research Institutions IV. TOT Centers of the University CONTENTS Sl.No. Particulars Page No. CHAIRMAN AND MEMBERS, BOARD OF MANAGEMENT .............................................................. 1 OFFICERS OF THE UNIVERSITY AND THEIR STAFF ........................................................................ 2 NORMAN BORLAUGE INTERNATIONAL CENTRE........................................................................... -

Navalgund Assembly Karnataka Factbook
Editor & Director Dr. R.K. Thukral Research Editor Dr. Shafeeq Rahman Compiled, Researched and Published by Datanet India Pvt. Ltd. D-100, 1st Floor, Okhla Industrial Area, Phase-I, New Delhi- 110020. Ph.: 91-11- 43580781-84 Email : [email protected] Website : http://www.indiastatelections.com Online Book Store : www.indiastatpublications.com Report No. : AFB/KA-069-0121 ISBN : 978-93-87148-28-4 First Edition : January, 2018 Third Updated Edition : January, 2021 Price : Rs. 11500/- US$ 310/- © Datanet India Pvt. Ltd. All rights reserved. No part of this book may be reproduced, stored in a retrieval system or transmitted in any form or by any means, mechanical photocopying, photographing, scanning, recording or otherwise without the prior written permission of the publisher. Please refer to Disclaimer at page no. 179 for the use of this publication. Printed in India Contents No. Particulars Page No. Introduction 1 Assembly Constituency - (Vidhan Sabha) at a Glance | Features of Assembly 1-2 as per Delimitation Commission of India (2008) Location and Political Maps Location Map | Boundaries of Assembly Constituency - (Vidhan Sabha) in 2 District | Boundaries of Assembly Constituency under Parliamentary 3-10 Constituency - (Lok Sabha) | Town & Village-wise Winner Parties- 2019, 2018, 2014, 2013 and 2009 Administrative Setup 3 District | Sub-district | Towns | Villages | Inhabited Villages | Uninhabited 11-15 Villages | Village Panchayat | Intermediate Panchayat Demographics 4 Population | Households | Rural/Urban Population -
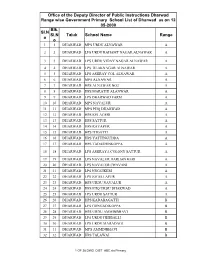
Sl.N O Blk. Sl.N O Taluk School Name Range Office Of
Office of the Deputy Director of Public Instructions Dharwad Range wise Government Primary School List of Dharwad as on 12- 05-2009 Blk. Sl.N Sl.N Taluk School Name Range o o 1 1 DHARWAD MPS URDU ALNAWAR A 2 2 DHARWAD LPS URDU RAHAMT NAGAR ALNAWAR A 3 3 DHARWAD LPS URDU VIDAY NAGAR ALNAWAR A 4 4 DHARWAD LPS TILAKNAGAR ALNAWAR A 5 5 DHARWAD LPS ASHRAY COL ALNAWAR A 6 6 DHARWAD MPS ALNAWAR A 7 7 DHARWAD HPS ALNAWAR NO2 A 8 8 DHARWAD HPS MARATHI ALANWAR A 9 9 DHARWAD LPS DHARWAD FARM A 10 10 DHARWAD MPS NAVALUR A 11 11 DHARWAD MPS PHQ DHARWAD A 12 12 DHARWAD HPS KELAGERI A 13 13 DHARWAD HPS SATTUR A 14 14 DHARWAD HPS RAYAPUR A 15 15 DHARWAD HPS ITIGATTI A 16 16 DHARWAD HPS YATTINGUDDA A 17 17 DHARWAD HPS TADASHINKOPPA A 18 18 DHARWAD LPS ASHRAYA COLONY SATTUR A 19 19 DHARWAD LPS NAVALUR HARIJAN KERI A 20 20 DHARWAD LPS NAVALUR CHAVANI A 21 21 DHARWAD LPS NUGGIKERI A 22 22 DHARWAD LPS JOGELLAPUR A 23 23 DHARWAD HPS URDU NAVALUR A 24 24 DHARWAD HPS PHQ URDU DHARWAD A 25 25 DHARWAD LPS URDU SATTUR A 26 26 DHARWAD HPS KADABAGATTI B 27 27 DHARWAD LPS GONGADIKOPPA B 28 28 DHARWAD HPS URDU AMMINBHAVI B 29 29 DHARWAD LPS URDU HEBBALLI B 30 30 DHARWAD LPS URDU MARADAGI B 31 31 DHARWAD MPS AMMINBHAVI B 32 32 DHARWAD HPS TALAWAI B 1 OF 28 DWD_DIST_ABC.xls Primary Range wise Government Primary School List of Dharwad as on 12- 05-2009 Blk. -

S.No Name of Grma Panchayat Identified
SLBC KARNATAKA: GRAM PANCHAYAT WISE SERVICE AREA PLAN OF THE DISTRICT: DHARWAR Name of the District: Dharwar Name Of the Block: BR./BC/A Name of Name of all revenue Post Identified TM Population Of the villages forming the GP Village Code Office/S Name of Grma place/village of Block existing Sl.N the Village as S.No allotted Used in 2011 ubpost Panchayat 2000+populatio Name or o. per Census bank with Census Office n(2001 census) proposed 2001 Branch YES/NO with name 1 AMMINBHAVI Dharwar BR 1 AMMINBHAVI 602299 10889 YES 2 ARAVATAGI Dharwar BC 2 AMBOLI 602248 1344 NO Dharwar BR 3 ARAVATAGI 602247 944 YES Dharwar BC 4 KOGILAGERI 602238 1204 NO Dharwar BC 5 KUMBARKOPPA 602250 1694 NO 3 BELUR BELUR Dharwar VIJAYA KOTUR BC 1 BEILUR 602226 2280 NO Dharwar BC 2 HEGGARI 602231 650 NO Dharwar BC 3 NEERALKATTI 602220 1251 NO 4 BENACHI Dharwar BC 1 BALAGERI 602238 1204 NO Dharwar BC 2 BENAGHI 602250 1696 YES Dharwar BC 3 DORI 602249 1696 NO 5 DEVARHUBLI Dharwar BC 1 DEVARHUBLI 602265 1954 NO Dharwar BC 2 MALLURA 602279 42 NO Dharwar BC 3 MURAKATTI 602264 822 NO 6 GARAG Dharwar BC 1 AGASANHALLI 602213 149 NO Dharwar BR 2 GARAG 602214 9422 YES 7 HALLIGERI Dharwar BC 1 AMLIKOPPA 602267 849 NO Dharwar BC 2 HALLIGERI 602266 1287 YES Dharwar BC 3 HULTIKOTI 602258 1134 NO Dharwar BC 4 MAVINKOPPA 602259 461 NO Dharwar BC 5 RAGIKALLAPUR NO 8 HANGARKI Dharwar BC 1 DUBBANAMARADI 620212 500 NO HANGARKI Dharwar KVGB TADAKOD BC 2 HANGARKI 602206 2003 NO Dharwar BC 3 KM TADAKOD 602199 695 NO Dharwar BC 4 SHEDABALA 602207 89 YES 9 HAROBELAVADI HAROBELAVADI Dharwar