Supplemental Notes on Series a Brief Introduction to Taylor and Power Series
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Line Integrals for Work, Circulation, and Plane Flux
Classroom Tips and Techniques: Line Integrals for Work, Circulation, and Plane Flux Robert J. Lopez Emeritus Professor of Mathematics and Maple Fellow © Maplesoft, a division of Waterloo Maple Inc., 2005 Introduction In our last column, we discussed how to address the iterated integral in Maple 9.5. This month, we will continue discussing integrals that arise in the subject area of vector calculus. In particular, we will discuss line integrals of the tangential and normal components of a vector field. The line integral of the tangential component of a force field produces the work done by the force on a particle of unit mass, as the mass moves along a specified curve. For the tangential component of the velocity field of a planar fluid flow, the line integral around a closed curve - typically a circle - is the circulation of the flow. The line integral of the normal component of a vector field is the flux of the field through the curve, and is a measure of the net "flow" of the field in the direction of the normal. If F = i + j represents the vector field in Cartesian coordinates, and is a planar curve parametrized by the equations then work (or circulation), the line integral of the tangential component of F along , is given by + or Flux, the line integral of the normal component of F along , is given by or (The mnemonic I always provided my students for the flux integral in the plane is that the form starts and ends with the same letters as the word "flux" and has a minus sign in the middle, thus determining where the letters and must go.) All of these physically meaningful quantities can be computed with the LineInt command in Maple's VectorCalculus package. -

Mathematics 1
Mathematics 1 MATH 1141 Calculus I for Chemistry, Engineering, and Physics MATHEMATICS Majors 4 Credits Prerequisite: Precalculus. This course covers analytic geometry, continuous functions, derivatives Courses of algebraic and trigonometric functions, product and chain rules, implicit functions, extrema and curve sketching, indefinite and definite integrals, MATH 1011 Precalculus 3 Credits applications of derivatives and integrals, exponential, logarithmic and Topics in this course include: algebra; linear, rational, exponential, inverse trig functions, hyperbolic trig functions, and their derivatives and logarithmic and trigonometric functions from a descriptive, algebraic, integrals. It is recommended that students not enroll in this course unless numerical and graphical point of view; limits and continuity. Primary they have a solid background in high school algebra and precalculus. emphasis is on techniques needed for calculus. This course does not Previously MA 0145. count toward the mathematics core requirement, and is meant to be MATH 1142 Calculus II for Chemistry, Engineering, and Physics taken only by students who are required to take MATH 1121, MATH 1141, Majors 4 Credits or MATH 1171 for their majors, but who do not have a strong enough Prerequisite: MATH 1141 or MATH 1171. mathematics background. Previously MA 0011. This course covers applications of the integral to area, arc length, MATH 1015 Mathematics: An Exploration 3 Credits and volumes of revolution; integration by substitution and by parts; This course introduces various ideas in mathematics at an elementary indeterminate forms and improper integrals: Infinite sequences and level. It is meant for the student who would like to fulfill a core infinite series, tests for convergence, power series, and Taylor series; mathematics requirement, but who does not need to take mathematics geometry in three-space. -

Problem Set 1
Mathematics 41C - 43C Mathematics Department Phillips Exeter Academy Exeter, NH August 2019 Table of Contents 41C Laboratory 0: Graphing . 6 Problem Set 1 . 9 Laboratory 1: Differences . 13 Problem Set 2 . .15 Laboratory 2: Functions and Rate of Change Graphs . 19 Problem Set 3 . .21 Laboratory 3: Approximating Instantaneous Rate of Change . 28 Problem Set 4 . .29 Laboratory 4: Linear Approximation . 34 Problem Set 5 . .36 Laboratory 5: Transformations and Derivatives . 41 Problem Set 6 . .43 Laboratory 6: Addition Rule and Product Rule for Derivatives . 47 Problem Set 7 . .49 Laboratory 7: Graphs and the Derivative . .53 Problem Set 8 . .54 Laboratory 8: The Most Exciting Moment on the Tilt-a-Whirl . 58 42C Laboratory 9: Graphs and the Second Derivative . 62 Problem Set 10 . .63 Laboratory 10: The Chain Rule for Derivatives . 66 Problem Set 11 . .69 Laboratory 11: Discovering Differential Equations . 74 Problem Set 12 . .76 Laboratory 12: Projectile Motion . .80 Problem Set 13 . .81 Laboratory 13: Introducing Slope Fields . .84 Problem Set 14 . .86 Laboratory 14: Introducing Euler's Method . 89 Problem Set 15 . .91 Laboratory 15: Skydiving . 95 Problem Set 16 . .97 43C Problem Set 17 . 102 Laboratory 17: The Gini Index . .107 Problem Set 18 . 111 Laboratory 18: Integration as Accumulation . .115 Problem Set 19 . 117 Laboratory 19: Geometric Probability . 120 Problem Set 20 . 121 August 2019 3 Phillips Exeter Academy Table of Contents Laboratory 20: The Normal Curve . 124 Problem Set 21 . 126 Laboratory 21: The Exponential Distribution . 129 Problem Set 22 . 131 Laboratory 22: Calculus and Data Analysis . 134 Problem Set 23 . 138 Laboratory 23: Predator/Prey Model . -
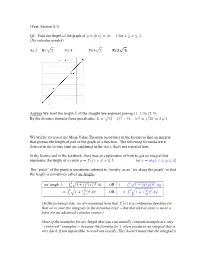
Lecture 19, March 1
(Text, Section 8.1) Q1: Find the length of the graph of for No calculus needed A) B) C) D) E) Answer We want the length of the straight line segment joining to By the distance formula from precalculus, We briefly reviewed the Mean Value Theorem (used later in the lecture to find an integral that givesus the length of part of the graph of a function. The following formulas were derived in the lecture (and are explained in the text): that's not repeated here. In the lecture and in the textbook, there was an explanation of how to get an integral that represents the length of a curve , (or The “piece” of the graph is sometimes referred to, loosely, as an “arc along the graph” so that the length is sometimes called arc length. arc length OR OR On the technical side, we are assuming here that is a continuous function (so that we're sure the integrals in the formulas exist but that find of issue is more a topic for an advanced calculus course.) Most of the examples for arc length that you can actually compute example are very “contrived” examples because the formula for often produces an integral that is very hard, if not impossible, to work out exactly. This doesn't mean that the integral is useless, however. Apart from certain theoretical uses, you can always write down the integral for any arc length and then use the Midpoint Rule, or some more sophisticated approximation rule, to approximate the value of the integral. For the Midpoint Rule, just pick as large an as you can tolerate working with, subdivide the interval into equal parts of length = , and plug into the formula for We can verify that these formulas do work in the simplest case (a straight line segment) which we did in Q1 without any calculus at all. -

Math 125: Calculus II - Dr
Math 125: Calculus II - Dr. Loveless Essential Course Info My Course Website: math.washington.edu/~aloveles/ Homework Log-In (use UWNetID): webassign.net/washington/login.html Directions for Webassign code purchase: math.washington.edu/webassign Math Department 125 Course Page: math.washington.edu/~m125/ First week to do list 1. Read 4.9, 5.1, 5.2, and 5.3 of the book. Start attempting HW. 2. Print off the “worksheets” and bring them to quiz sections. Today 1st HW assignments Syllabus/Intro Closing time is always 11pm. Section 4.9 - HW1A,1B,1C close Oct 4 - antiderivatives (Wed) (covers 4.9, 5.1, and 5.2) Expect 6-8 hrs of work, start today! What we will do in this course: 4. Ch. 8-9 – More Applications We learn the basic tools of integral - Arc Length, Center of Mass calculus which provide the essential - Differential Equations language for engineering, science and economics. Specifically, 5. Practicing Algebra, Trig and Precalc Students often say: The hardest part 1. Ch. 5 – Defining the Integral of calculus is you have to know all - Definition and basic techniques your precalculus, and they are right. 2. Ch. 6 – Basic Integral Applications Improving your algebra, trig and - Areas, Volumes precalculus skills will be one of the - Average Value best benefits you will gain from this - Measuring Work course (arguably as valuable as the course content itself). You will use 3. Ch. 7 – Integration Techniques these skills often in your other - by parts, trig, trig sub, partial courses at UW. frac Entry Task: Differentiate 7 1. 퐹(푥) = − 5√푥3 + 4ln (푥) 푥10 6푥 2. -

Notation Guide for Precalculus and Calculus Students
Notation Guide for Precalculus and Calculus Students Sean Raleigh Last modified: August 27, 2007 Contents 1 Introduction 5 2 Expression versus equation 7 3 Handwritten math versus typed math 9 3.1 Numerals . 9 3.2 Letters . 10 4 Use of calculators 11 5 General organizational principles 15 5.1 Legibility of work . 15 5.2 Flow of work . 16 5.3 Using English . 18 6 Precalculus 21 6.1 Multiplication and division . 21 6.2 Fractions . 23 6.3 Functions and variables . 27 6.4 Roots . 29 6.5 Exponents . 30 6.6 Inequalities . 32 6.7 Trigonometry . 35 6.8 Logarithms . 38 6.9 Inverse functions . 40 6.10 Order of functions . 42 7 Simplification of answers 43 7.1 Redundant notation . 44 7.2 Factoring and expanding . 45 7.3 Basic algebra . 46 7.4 Domain matching . 47 7.5 Using identities . 50 7.6 Log functions and exponential functions . 51 7.7 Trig functions and inverse trig functions . 53 1 8 Limits 55 8.1 Limit notation . 55 8.2 Infinite limits . 57 9 Derivatives 59 9.1 Derivative notation . 59 9.1.1 Lagrange’s notation . 59 9.1.2 Leibniz’s notation . 60 9.1.3 Euler’s notation . 62 9.1.4 Newton’s notation . 63 9.1.5 Other notation issues . 63 9.2 Chain rule . 65 10 Integrals 67 10.1 Integral notation . 67 10.2 Definite integrals . 69 10.3 Indefinite integrals . 71 10.4 Integration by substitution . 72 10.5 Improper integrals . 77 11 Sequences and series 79 11.1 Sequences . -

CALCULUS I – REVIEW Things to Know Precalculus (Prerequisite Material). Sections 1.1 – 1.3 • Functions, Graphs, Function C
CALCULUS I { REVIEW ALLAN YASHINSKI Abstract. The following document evolved from several \study guides" which were written to help Math 241 (Calculus I) students at the University of Hawaii at Manoa prepare for exams. The section references are for University Calcu- lus, Alternate Edition by Hass, Weir, and Thomas. Things to know Precalculus (Prerequisite Material). Sections 1.1 { 1.3 • Functions, graphs, function composition f ◦ g. • Trigonometry, the six basic trigonometric functions. You should know the values of the trig functions on angles like 0; π=6; π=4; π=3; π=2; and the corresponding angles in other quadrants. Limits and Continuous Functions. Sections 2.2, 2.4, 2.5, 2.6 • To say lim f(x) = L means that the values (the output) of the function x!c f(x) get closer and closer to the number L when we consider x (the input) closer and closer to c. The function f does not even have to be defined at x = c, and even if it is, the value f(c) does not influence what the limit is. In other words, it doesn't matter what is happening at x = c; limits are all about what is happening near x = c. • The Limit Laws Suppose that lim f(x) and lim g(x) exist. Then x!c x!c lim (f(x) + g(x)) = lim f(x) + lim g(x) , x!c x!c x!c lim (f(x) − g(x)) = lim f(x) − lim g(x) , x!c x!c x!c lim (f(x) · g(x)) = lim f(x) lim g(x) , x!c x!c x!c lim (k · f(x)) = k lim f(x) for any constant k, x!c x!c f(x) lim f(x) lim = x!c , provided lim g(x) 6= 0, x!c g(x) limx!c g(x) x!c r lim (f(x))r = lim f(x) , for any exponent r, as long as the expres- x!c x!c sion makes sense. -
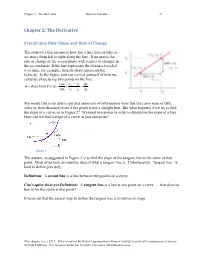
Chapter 2: the Derivative
Chapter 2 The Derivative Business Calculus 73 Chapter 2: The Derivative Precalculus Idea: Slope and Rate of Change The slope of a line measures how fast a line rises or falls as we move from left to right along the line. It measures the rate of change of the y-coordinate with respect to changes in the x-coordinate. If the line represents the distance traveled over time, for example, then its slope represents the velocity. In the figure, you can remind yourself of how we calculate slope using two points on the line: rise y2 − y1 ∆y m = slope from P to Q = = = run x2 − x1 ∆x We would like to be able to get that same sort of information (how fast the curve rises or falls, velocity from distance) even if the graph is not a straight line. But what happens if we try to find the slope of a curve, as in Figure 2? We need two points in order to determine the slope of a line. How can we find a slope of a curve, at just one point? Figure 1 The answer, as suggested in Figure 2 is to find the slope of the tangent line to the curve at that point. Most of us have an intuitive idea of what a tangent line is. Unfortunately, “tangent line” is hard to define precisely. Definition: A secant line is a line between two points on a curve. Can’t-quite-do-it-yet Definition: A tangent line is a line at one point on a curve …. -
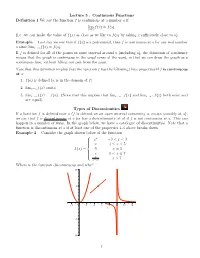
Lecture 5 : Continuous Functions Definition 1 We Say the Function F Is
Lecture 5 : Continuous Functions Definition 1 We say the function f is continuous at a number a if lim f(x) = f(a): x!a (i.e. we can make the value of f(x) as close as we like to f(a) by taking x sufficiently close to a). Example Last day we saw that if f(x) is a polynomial, then f is continuous at a for any real number a since limx!a f(x) = f(a). If f is defined for all of the points in some interval around a (including a), the definition of continuity means that the graph is continuous in the usual sense of the word, in that we can draw the graph as a continuous line, without lifting our pen from the page. Note that this definition implies that the function f has the following three properties if f is continuous at a: 1. f(a) is defined (a is in the domain of f). 2. limx!a f(x) exists. 3. limx!a f(x) = f(a). (Note that this implies that limx!a− f(x) and limx!a+ f(x) both exist and are equal). Types of Discontinuities If a function f is defined near a (f is defined on an open interval containing a, except possibly at a), we say that f is discontinuous at a (or has a discontinuiuty at a) if f is not continuous at a. This can happen in a number of ways. In the graph below, we have a catalogue of discontinuities. Note that a function is discontinuous at a if at least one of the properties 1-3 above breaks down. -

Reavis High School AP Calculus Curriculum Snapshot
Reavis High School AP Calculus Curriculum Snapshot Unit 1: Preparation for Calculus Review of Algebra II Honors and Precalculus In this unit, students will review concepts learned in Algebra II/Precalculus. Students will be graphing and writing equations of lines using various methods as well as applying these 6 - 7 concepts in real-life situations. In addition, we will review Days evaluating functions and identify different types of transformations followed by obtaining appropriate lines for linear, quadratic, and cubic models to better understand the connections among these representations. Unit 2: Limits and Their Properties In this unit, students will obtain an intuitive understanding of the limit process. We will be calculating limits using algebra 9 and estimating those using graphs and tables of values, Days followed by finding asymptotes of different functions. Finally, we will investigate limits involving infinity and understand continuity of functions in terms of limits. Unit 3: Differentiation In this unit, we will define and understand the meaning of derivatives in terms of rate of change and linear 18 approximation. We will calculate derivatives of functions Days written in different forms using graphical, numerical, and analytical approaches. Finally, we will be able to apply this knowledge to solve real life problems using related rates. Unit 4: Applications of Differentiation In this unit, we will apply our understanding of derivatives to analyze curves of different functions. As a result, we will be 20 - 21 able to identify extrema of any function on both open and closed intervals and finally sketch the graph without using a Days calculator. In addition, we will use differentiation to solve optimization problems which will require us to use maximum and minimum values in real-life situations. -

SYLLABUS MATH 12012 –Calculus with Precalculus II
SYLLABUS MATH 12012 –Calculus with Precalculus II (3 Credit Hours) Catalog Information: Development of integral calculus and continued study of differential calculus. Includes curve sketching optimization fundamental theorem of calculus areas between curves, exponential and logarithmic functions. No credit earned for this course if student earned credit for MATH 12002. Prerequisite: MATH 12011 with a minimum grade of C (2.0). Text: Precalculus and Calculus I and II, 5th Edition, Stewart, Cengage. MATH 12011 and MATH 12012 are three credit hour courses that together cover the same Calculus topics as MATH 12002, Analytic Geometry and Calculus I. In addition, each course includes review of appropriate topics from Algebra and Trigonometry as they are needed. The outline below follows the Calculus syllabus, with sections and topics from precalculus listed where appropriate. The review sections (labeled Precalc) should be used only as a guide. It is not anticipated that every section will be covered in detail | these are simply the sections where the appropriate review material appears. The particular topics to be covered from each precalculus section are at the discretion of the instructor. Review topics are indicated by boldfaced type. Applications of Derivatives, Curve Sketching and Optimization (12 classes): Precalc: §1.7 (and §1.3 – 1.5 if needed), §7.5 (optional) Calc: §§4.3 – 4.9 Review of solving equations and non-linear inequalities by factoring, including factoring of rational expressions arising as derivatives. Increasing/decreasing functions, local maxima and minima, concavity, inflection points, review infinite limits (Calc §1.2), limits at infinity, asymptotes, curve sketching, applied optimization problems. [Calc 10, Precalc 2] Integration (9 classes): Calc: §§4.10, 5.1 – 5.5 Areas and distances, Riemann sums, the definite integral, antiderivatives, Fundamental Theorem of Calculus, indefinite integrals, integration by substitution. -
Answers (Lesson 1-3)
AA01_A20_PCCRMC01_893802.indd 7 0 1 _ A 2 0 _ P C C R M C Copyright © Glencoe/McGraw-Hill, a division of The McGraw-Hill Companies, Inc. 0 1 _ 8 9 3 8 0 Chapter 1 2 . i n d d NAME DATE PERIOD NAME DATE PERIOD 7 A7 1-3 Study Guide and Intervention 1-3 Study Guide and Intervention (continued) Continuity, End Behavior, and Limits Continuity, End Behavior, and Limits Continuity A function f(x) is continuous at x = c if it satisfies the End Behavior The end behavior of a function describes how the function behaves at following conditions. either end of the graph, or what happens to the value of f(x) as x increases or decreases without bound. You can use the concept of a limit to describe end behavior. (1) f(x) is defined at c; in other words, f(c) exists. (2) f(x) approaches the same function value to the left and right of c; in other Left-End Behavior (as x becomes more and more negative): lim f(x) x → -∞ words, lim f x exists. ( ) x → c Right-End Behavior (as x becomes more and more positive): lim f(x) (3) The function value that f(x) approaches from each side of c is f(c); in x → ∞ The f(x) values may approach negative infinity, positive infinity, or a specific value. other words, lim f(x) = f(c). x → c Functions that are not continuous are discontinuous. Graphs that are Example Use the graph of f(x) x3 2 to describe y discontinuous can exhibit infinite discontinuity, jump discontinuity, = + 8 its end behavior.